Как найти площадь основания октаэдра - Сайт, где вы сможете решить свои вопросы

Октаэдр и площадь полной его поверхности: описание, формулы, примеры

Содержание:

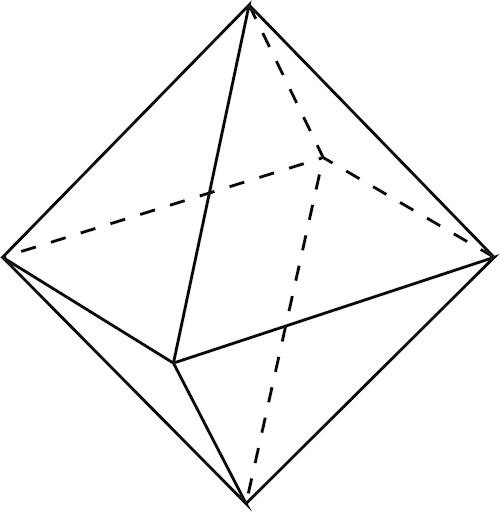
Существует несколько способов определить площадь поверхности октаэдра. Он представляет собой один из пяти правильных многоугольников или так называемых Платоновых тел. Имеет восемь одинаковых граней (поверхностей) в виде равносторонних треугольников, к каждой из его вершин прилагается по четыре грани. Рассмотрим, что собой представляет тело, где встречается в природе, как вычисляется его площадь и объём.

Что такое октаэдр

Свойства октаэдра

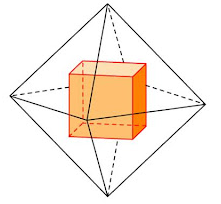
В тело вписывается куб, вершины которого находятся в центрах граней куба.

Симметрия куба и вписанного (описанного) октаэдра совпадают.

Двойственен кубу.

Является полным усечением тетраэдра.

Имеет равные ребра и диагонали.

Состоит из равносторонних треугольников.

Диагонали тела взаимоперпендикулярны, в точке пересечения делятся на равные отрезки.

Октаэдр симметричен, причём 3 оси пролегают через противоположные вершины, 6 – через центры ребер.

Центр симметрии тела расположен в точке пересечения диагоналей.

Ребра равны по длине, поверхности – по площади.

Математические характеристики тела

Как вычислить площадь поверхности октаэдра

Площадь октаэдра равна сумме площадей составляющих его треугольников:

Здесь S_треуг – площадь треугольника.

После подстановки значения получится требуемый результат.

Если известна длина ребра, придётся вычислить площадь треугольников.

Подставляем значение в первое выражение:

Упрощаем: после сокращения дроби на четыре получается формула площади поверхности октаэдра:

2. S = 8 * S_треуг = 2 sqrt <3>a^2.

Существует ещё один способ проведения вычислений. Он менее точный чем предыдущие, однако позволяет обойтись без калькулятора. При приблизительном подсчёте 2 sqrt <3>равняется 3,464 или 3,46.

Здесь a – длина стороны треугольника (равны).

Для примера, имеется фигура октаэдр с длиной стороны 5 см.

S=2sqrt <3>a^2=2*sqrt <3>*5^2=2*sqrt <3>*25=50sqrt <3>approx 86,6 см.

Как вычислить объём правильного октаэдра

Объём показывает размер внутреннего пространства геометрического тела. Объем правильного октаэдра вычисляется, если знаете длину ребра геометрического тела, по формуле:

После проведения приблизительных расчётов frac<sqrt 2> <3>approx 0,47 формула принимает следующий вид :

Рассчитаем двумя методами на примере правильного многоугольника с гранью, равной 5 см:

V= 0,47 * a^3 = 0,47*125 approx 58,93

Значения совпали, во втором случае нужно выполнять гораздо меньше операций. Подходит он только, если не требуется исключительная точность – при округлении до 4-5 знаков после запятой точность снизится.

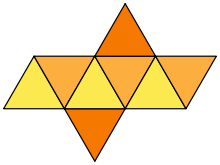
Развёртка

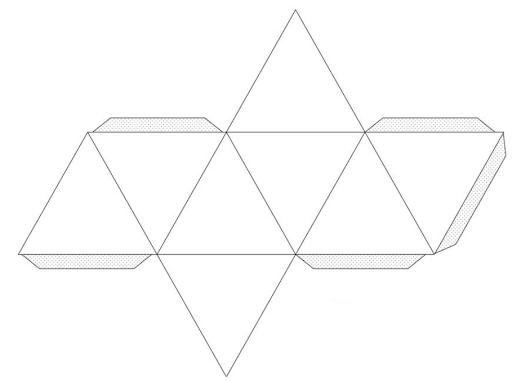
Октаэдр, как большинство гомерических тел, имеет развёртку поверхности – это плоская фигура, полученная путём совмещения поверхности модели с одной плоскостью без пересечения либо наложения граней друг на друга.

Рисунок развёртки октаэдра.

В природе насчитывается 11 разновидностей развёртки октаэдра, позволяющих создать его модель из бумаги или картона. Наиболее распространённая выглядит как восемь одинаковых треугольников. Шесть из них размещено в ряд, к третьему и четвёртому основаниям прилегает ещё по одному, их вершины направлены в противоположные стороны.

Октаэдр.

Октаэдр — один из 5-ти выпуклых правильных многогранников – Платоновых тел.

У октаэдра 8 треугольных граней, 12 рёбер, 6 вершин, к каждой его вершине сходятся 4 ребра.

На примере октаэдра легко проверить формулу Эйлера 6в+8г-12р=2. В каждой из вершин октаэдра сходятся 4 треугольника, т.о., сумма плоских углов у вершины октаэдра равна 240°. Из понятия правильного многогранника делаем вывод, что каждое ребра октаэдра имеет одинаковую длину, а грань – одинаковую площадь.

Обозначим длину ребра октаэдра как а, значит площадь полной поверхности октаэдра (S) и объём октаэдра (V) найдем из таких формул:

Радиус описанной сферы около октаэдра:

Радиус вписанной сферы около октаэдра:

Сумма длин всех ребер равна 24а.

Двугранный угол: α=2ϕ≈109,47°, где .

Свойства октаэдра.

Октаэдр легко вписывается в тетраэдр, при этом 4 из 8-ми граней октаэдра совместятся с 4-мя гранями тетраэдра, каждая из 6-ти вершин октаэдра совместится с центрами 6-ти ребер тетраэдра.

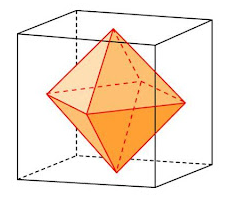
Октаэдр легко вписывается в куб (гексаэдр), при этом каждая из 6-ти вершин октаэдра совместится с центрами 6-ти граней куба.

В октаэдр легко вписать куб, при этом каждая из 8-ми вершин куба будут располагаться в центрах 8-ми граней октаэдра.

У правильного октаэдра есть симметрия O_h, которая совпадает с симметрией куба.

Развёртка октаэдра.

Симметрия октаэдра.

3 из девяти осей симметрии октаэдра проходят сквозь противолежащие

вершины, 6 – квозь середины ребер.

Центр симметрии октаэдра – точка пересечения осей симметрии октаэдра.

3 из девяти плоскостей симметрии тетраэдра проходят сквозь все 4 вершины октаэдра, которые лежат в одной плоскости.

6 плоскостей симметрии проходят через 2 вершины, которые не принадлежат одной грани, и середины противолежащих ребер.

Октаэдр

Древние греки дали многограннику имя по числу граней. «Окто» означает восемь, «хедра» – означает грань (октаэдр – восьмигранник).

Поэтому на вопрос – “что такое октаэдр?”, можно дать следующее определение: ” Октаэдр это геометрическое тело из восьми граней, каждая их которых – правильный треугольник “.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .

Октаэдр имеет следующие характеристики:

Тип грани – правильный треугольник;
Число сторон у грани – 3;
Общее число граней – 8;
Число рёбер, примыкающих к вершине – 4;
Общее число вершин – 6;
Общее число рёбер – 12;

Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.

Октаэдр имеет центр симметрии – центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.

Математические характеристики октаэдра

Октаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы октаэдра определяется по формуле:

, где a – длина стороны.

Сфера может быть вписана внутрь октаэдра.

Радиус вписанной сферы октаэдра определяется по формуле:

Площадь поверхности октаэдра

Для наглядности, площадь поверхности октаэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон октаэдра (это площадь правильного треугольника) умноженной на 8. Либо воспользоваться формулой:

Объем октаэдра определяется по следующей формуле:

Октаэдр можно представить в виде двух правильных пирамид с четырехугольным основанием, соединенных друг с другом через это основание.

Вариант развертки

Октаэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка – единая деталь с линиями сгибов.

Древнегреческий философ Платон ассоциировал октаэдр с “земным” элементом воздух, поэтому для построения модели этого правильного многогранника мы выбрали серый цвет.

Заметим, что это не единственный вариант развертки.

Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
– если Вы предполагаете распечатать на цветном принтере – цветная развертка
– если Вы предполагаете использовать для сборки цветной картон – развертка

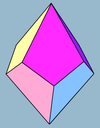
Классический вариант раскраски предполагает окраску октаэдра четырьмя различными цветами, причем таким образом, что каждая грань имеет свой цвет отличный от соседней и только противоположные не соприкасающиеся друг с другом грани окрашиваются в одинаковые цвета.

Вариант окраски представлен на рисунке. Вы можете скачать развертку с соответствующей раскраской граней.

Видео. Октаэдр из набора “Волшебные грани”

Вы можете изготовить модель октаэдра воспользовавшись деталями для сборки из набора “Волшебные грани”.

Сборка многогранника из набора:

Подробная сборка от Алексея Жигулева (youtube-канал PRO)

вращение готового многогранника:

Видео. Вращение правильных многогранников

[spoiler title=”источники:”]

http://www.calc.ru/Oktaedr.html

http://mnogogranniki.ru/oktaedr.html

[/spoiler]

Источник

Вы здесь:

Главная
Октаэдр

Октаэдр

Поэтому на вопрос – “что такое октаэдр?”, можно дать следующее определение: “Октаэдр это геометрическое тело из восьми граней, каждая их которых – правильный треугольник“.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел.

Октаэдр имеет следующие характеристики:

Тип грани – правильный треугольник;
Число сторон у грани – 3;
Общее число граней – 8;
Число рёбер, примыкающих к вершине – 4;
Общее число вершин – 6;
Общее число рёбер – 12;

Октаэдр имеет центр симметрии – центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.

Математические характеристики октаэдра

Радиус описанной сферы октаэдра определяется по формуле:

, где a – длина стороны.

Сфера может быть вписана внутрь октаэдра.

Радиус вписанной сферы октаэдра определяется по формуле:

Площадь поверхности октаэдра

Объем октаэдра определяется по следующей формуле:

Правильный октаэдр[править | править код]

Правильный октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.

Размеры[править | править код]

Если длина ребра октаэдра равна а, то радиус сферы, описанной вокруг октаэдра, равен:

$r_u = frac{a}{2} sqrt{2} approx 0.7071067 cdot a$ ,

радиус вписанной в октаэдр сферы может быть вычислен по формуле:

$r_i = frac{a}{6} sqrt{6}approx 0.4082482cdot a .$

двугранный угол: ${textstyle alpha =2varphi approx 109,47^{circ }}$ , где ${textstyle varphi =arccos left({frac {sqrt {3}}{3}}right)}$ .

Радиус полувписанной сферы, которая касается всех рёбер, равен

$r_m = frac{a}{2} = 0.5cdot a$

Ортогональные проекции[править | править код]

Октаэдр имеет четыре специальные ортогональных проекции, центрированные ребром, вершиной, гранью и нормалью к грани. Второй и третий случай соответствуют плоскостям Коксетера B₂ и A₂.

Ортогональные проекции

Центрированы	Ребром	Нормалью к грани	Вершиной	Гранью
Образ
Проективная симметрия	[2]	[2]	[4]	[6]

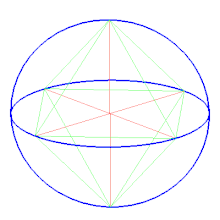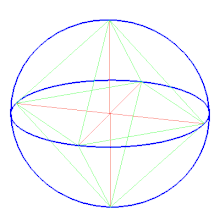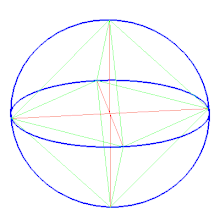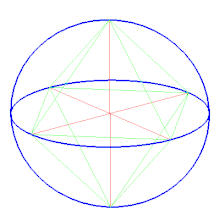
Сферическая мозаика[править | править код]

Октаэдр можно представить, как сферическую мозаику и спроецировать на плоскость с помощью стереографической проекции. Эта проекция конформна, сохраняет углы, но не длины и площадь. Отрезки на сфере отображаются в дуги окружностей на плоскости.

Ортогональная проекция	Стереографическая проекция
	треугольно-центрированная

Декартовы координаты[править | править код]

Октаэдр с длиной ребра может быть помещён в начало координат, так что его вершины будут лежать на осях координат. Декартовы координаты вершин тогда будут

(±1, 0, 0);

(0, ±1, 0);

(0, 0, ±1).

В x–y–z прямоугольной системе координат октаэдр с центром в точке (a, b, c) и радиусом r — это множество всех точек (x, y, z), таких, что

left|x - aright| + left|y - bright| + left|z - cright| = r.

Площадь и объём[править | править код]

Площадь полной поверхности правильного октаэдра с длиной ребра a равна

$S=2a^2sqrt{3} approx 3.46410162a^2$

Объём октаэдра (V) вычисляется по формуле:

$V=begin{matrix}{1over3}end{matrix}sqrt{2}a^3 approx 0.471404521a^3$

Таким образом, объём октаэдра в четыре раза больше объёма тетраэдра с той же длиной ребра, в то время как площадь поверхности вдвое больше (поскольку поверхность состоит из 8 треугольников, а у тетраэдра — из четырёх).

Если октаэдр растянуть, чтобы выполнялось равенство:

$left|frac{x}{x_m}right|+left|frac{y}{y_m}right|+left|frac{z}{z_m}right| = 1,$

формулы для поверхности и объёма превращаются в:

$A=4 , x_m , y_m , z_m times sqrt{frac{1}{x_m^2}+frac{1}{y_m^2}+frac{1}{z_m^2}}$

$V=frac{4}{3},x_m,y_m,z_m$

Кроме того, тензор моментов инерции растянутого октаэдра будет равен:

$I = begin{bmatrix} frac{1}{10} m (y_m^2+z_m^2) & 0 & 0 \ 0 & frac{1}{10} m (x_m^2+z_m^2) & 0 \ 0 & 0 & frac{1}{10} m (x_m^2+y_m^2) end{bmatrix}$

Он сводится к уравнению для правильного октаэдра, когда: ${textstyle x_{m}=y_{m}=z_{m}=a,{frac {sqrt {2}}{2}}}$

Геометрические связи[править | править код]

Октаэдр представляет собой пересечение двух тетраэдров

Внутренняя (общая) часть конфигурации из двух двойственных тетраэдров является октаэдром, а сама эта конфигурация называется звёздчатым октаэдром (лат.: stella octangula). Конфигурация является единственной звёздчатой формой октаэдра. Соответственно, правильный октаэдр является результатом отсечения от правильного тетраэдра четырёх правильных тетраэдров с половиной длины ребра (то есть полного усечения тетраэдра). Вершины октаэдра лежат на серединах рёбер тетраэдра и октаэдр связан с тетраэдром тем же образом, как кубооктаэдр и икосододекаэдр связаны с остальными платоновыми телами. Можно разделить рёбра октаэдра в отношении золотого сечения для определения вершин икосаэдра. Для этого следует расположить вектора на рёбрах, так, чтобы все грани были окружены циклами. Затем делим каждое ребро в золотом отношении вдоль векторов. Полученные точки являются вершинами икосаэдра.

Октаэдры и тетраэдры^[en] можно чередовать, чтобы построить однородные относительно вершин, рёбер и граней соты, которые Фуллер назвал октетной связкой^[en]. Это единственные соты, позволяющие регулярную укладку в кубе, и они являются одним из 28 видов выпуклых однородных сот^[en].

Октаэдр уникален среди платоновых тел в том, что только он имеет чётное число граней при каждой вершине. Кроме того, это единственный член этой группы, который имеет плоскости симметрии, не пересекающие ни одну грань.

Если использовать стандартную терминологию многогранников Джонсона, октаэдр можно назвать квадратной бипирамидой. Усечение двух противоположных вершин приводит к усечённой бипирамиде^[en].

Октаэдр является 4-связным. Это значит, что нужно удалить четыре вершины, чтобы разъединить оставшиеся. Это один из всего лишь четырёх 4-связных симплициальных хорошо покрытых многогранников, что означает, что все наибольшие независимые множества вершин имеют один и тот же размер. Другие три многогранника с этим свойством — пятиугольная бипирамида, плосконосый двуклиноид и нерегулярный многогранник с 12 вершинами и 20 треугольными гранями^[2].

Октаэдр можно вписать в тетраэдр, притом четыре из восьми граней октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести ребер тетраэдра.
Октаэдр можно вписать в куб, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
В октаэдр можно вписать куб, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.

Однородное раскрашивание и симметрия[править | править код]

Имеется 3 однородных раскрашивания^[en] октаэдра, названных по их цветам граней: 1212, 1112, 1111.

Группой симметрии октаэдра является O_h с порядком 48, трёхмерная гипероктаэдральная группа^[en]. В подгруппы этой группы входят D_3d (порядка 12), группа симметрии треугольной антипризмы, D_4h (порядка 16), группа симметрии квадратной бипирамиды, и T_d (порядка 24), группа симметрии полностью усечённого тетраэдра. Эти симметрии можно подчеркнуть путём различного раскрашивания граней.

Название	Октаэдр	Полностью усечённый тетраэдр (Тетратетраэдр)	Треугольная антипризма	Квадратная бипирамида	Ромбическая бипирамида
Рисунок (Раскраска граней)	(1111)	(1212)	(1112)	(1111)	(1111)
Диаграмма Коксетера		=
Символ Шлефли	{3,4}	r{3,3}	s{2,6} sr{2,3}	ft{2,4} { } + {4}	ftr{2,2} { } + { } + { }
Символ Витхоффа^[en]	4 \| 3 2	2 \| 4 3	2 \| 6 2 \| 2 3 2
Симметрия	O_h, [4,3], (*432)	T_d, [3,3], (*332)	D_3d, [2⁺,6], (2*3) D₃, [2,3]⁺, (322)	D_4h, [2,4], (*422)	D_2h, [2,2], (*222)
Порядок	48	24	12 6	16	8

Развёртки[править | править код]

Существует одиннадцать вариантов развёртки октаэдра^[3].

Двойственность[править | править код]

Октаэдр двойственен кубу.

Огранка[править | править код]

Однородный тетрагемигексаэдр является огранкой с тетраэдральной симметрией правильного октаэдра, сохраняющая расположение рёбер^[en] и вершин^[en]. Огранка имеет четыре треугольных грани и 3 центральных квадрата.

Неправильные октаэдры[править | править код]

Следующие многогранники комбинаторно эквивалентны правильному октаэдру. Они все имеют шесть вершин, восемь треугольных граней и двенадцать рёбер, что соответствует один к одному параметрам правильного октаэдра.

Треугольные антипризмы — две грани представляют собой равносторонние треугольники, лежащие в параллельных плоскостях и имеющие общую ось симметрии. Остальные шесть треугольников равнобедренные.
Четырёхугольные бипирамиды, в которых по меньшей мере один экваториальный четырёхугольник лежит в плоскости. Правильный октаэдр является специальным случаем, когда все три четырёхугольника являются плоскими квадратами.
Многогранник Шёнхардта, невыпуклый многогранник, который нельзя разбить на тетраэдры без введения новых вершин.

Другие выпуклые восьмигранники[править | править код]

Четырёхугольный
трапецоэдр

В общем случае, октаэдром может называться любой многогранник с восемью гранями. Правильный октаэдр имеет 6 вершин и 12 рёбер, минимальное число для октаэдра. Неправильные восьмигранники могут иметь до 12 вершин и 18 рёбер^[3]^[4].
Существует 257 топологически различных выпуклых восьмигранников, исключая зеркальные копии^[3]. В частности, имеется 2, 11, 42, 74, 76, 38, 14 восьмигранников с числом вершин от 6 до 12 соответственно^[5]^[6]. (Два многогранника «топологически различны», если они имеют внутренне различное расположение граней и вершин, так что нет возможности преобразовать одно тело в другое просто изменением длины рёбер или углов между рёбрами или гранями.)

Некоторые известные неправильные восьмигранники:

Шестиугольная призма: Две грани являются параллельными правильными шестиугольниками, шесть квадратов соединяют соответствующие пары сторон шестиугольников.
Семиугольная пирамида: Одна грань является семиугольником (обычно правильным), а оставшиеся семь граней являются треугольниками (обычно равнобедренными). Невозможно добиться, чтобы все треугольные грани были равносторонними.
Усечённый тетраэдр: Четыре грани тетраэдра усекаются до правильных шестиугольников и образуются три дополнительные равносторонние треугольные грани на месте отсечённых вершин.
Четырёхугольный трапецоэдр: Восемь граней конгруэнтны дельтоидам.

Октаэдры в физическом мире[править | править код]

Октаэдры в природе[править | править код]

Многие природные кубические кристаллы имеют форму октаэдра. Это алмаз (у которого также спайность по октаэдру)^[7], сульфат алюминия-калия, хлорид натрия, перовскит, оливин, флюорит, шпинель.
Форму октаэдра имеют межатомные пустоты (поры) в плотноупакованных структурах чистых металлов (никеле, меди, магнии, титане, лантане и многих других) и ионных соединений (хлорид натрия, сфалерит, вюрцит и др.).
Пластины сплава камасита^[en] в октаэдритных метеоритах расположены параллельно восьми граням октаэдра.

Октаэдры в искусстве и культуре[править | править код]

Две одинаково сложенные змейки Рубика могут аппроксимировать октаэдр.

В играх игральная кость в виде октаэдра известна как «d8».
Если каждое ребро октаэдра заменить одноомным резистором, общее сопротивление между противоположными вершинами будет составлять 1/2 ома, а между смежными вершинами — 5/12 ома^[8].
Шесть музыкальных нот можно расположить на вершинах октаэдра так, что каждое ребро представляет созвучную пару, а каждая грань — созвучную тройку.
Противотанковый ёж имеет форму трёх диагоналей октаэдра.

Тетраэдральная связка[править | править код]

Каркас из повторяющихся тетраэдров и октаэдров изобретён Фуллером в 1950-х и он известен как пространственная рама^[en] и считается прочнейшей структурой, сопротивляющейся напряжениям консольной балки.

Связанные многогранники[править | править код]

Правильный октаэдр можно увеличить до тетраэдра добавлением четырёх тетраэдров на чередующиеся грани. Добавление тетраэдров ко всем восьми граням образует звёздчатый октаэдр.

тетраэдр	звёздчатый октаэдр

Октаэдр принадлежит семейству однородных многогранников, связанных с кубом.

Однородные октаэдральные многогранники

Симметрия: [4,3], (*432)^[en]	[4,3]⁺, (432)	[3⁺,4], (3*2)


{4,3}	t{4,3}	r{4,3}	t{3,4}	{3,4}	rr{4,3}	tr{4,3}	sr{4,3}	s{3,4}
Двойственные многогранники

V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3⁵

Он также является одним из простейших примеров гиперсимплекса^[en], многогранника, образованного определённым пересечением гиперкуба с гиперплоскостью.

Октаэдр входит в последовательность многогранников с символом Шлефли {3,n}, продолжающейся на гиперболическую плоскость.

*n32 симметрии правильных мозаик: 3ⁿ or {3,n}

Сферическая	Евклидова	Компактная гипербол.	Пара- компактная	Некомпактная гиперболическая

3.3	3³	3⁴	3⁵	3⁶	3⁷	3⁸	3^∞	3¹²ⁱ	3⁹ⁱ	3⁶ⁱ	3³ⁱ

Тетратетраэдр[править | править код]

Правильный октаэдр можно рассматривать как полностью усечённый тетраэдр и может быть назван тетратетраэдром. Это можно показать с помощью раскрашенной в два цвета модели. При этом раскрашивании октаэдр имеет тетраэдральную симметрию.

Сравнение последовательности усечения тетраэдра и его двойственной фигуры:

Семейство однородных тетраэдральных многогранников

Симметрия: [3,3], (*332)	[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Двойственные многогранники

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Вышеприведённые тела можно понимать как срезы, ортогональные к длинной диагонали тессеракта. Если расположить эту диагональ вертикально с высотой 1, то первые пять сечений сверху будут на высотах r, 3/8, 1/2, 5/8 и s, где r — любое число в интервале (0,1/4], а s — любое число в интервале [3/4,1).

Октаэдр в качестве тетратетраэдра существует в последовательности симметрий квазиправильных многогранников и мозаик с конфигурацией вершин (3.n)², проходя от мозаик на сфере к евклидовой плоскости, а затем в гиперболическую плоскость. В орбифолдной нотации^[en] симметрии *n32 все эти мозаики являются построениями Витхоффа внутри фундаментальной области симметрии с генерирующими точками на прямом угле области^[9]^[10].

*n32 орбифолдные симметрии квазирегулярных мозаик: (3.n)²

Построение	Сферическая	Евклидова	Гиперболическая
*332	*432	*532	*632	*732	*832…	*∞32
Квазирегулярные фигуры
Вершина	(3.3)²	(3.4)²	(3.5)²	(3.6)²	(3.7)²	(3.8)²	(3.∞)²

Треугольная антипризма[править | править код]

В качестве треугольной антипризмы октаэдр связан с семейством шестиугольной диэдральной симметрии.

Однородные шестиугольные диэдральные сферические многогранники

Симметрия: [6,2], (*622)	[6,2]⁺, (622)	[6,2⁺], (2*3)


{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{2,6}	tr{6,2}^[en]	sr{6,2}	s{2,6}
Двойственные им многогранники

V6²	V12²	V6²	V4.4.6^[en]	V2⁶	V4.4.6^[en]	V4.4.12	V3.3.3.6^[en]	V3.3.3.3

Семейство однородных антипризм n.3.3.3

Конфигурация	V2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	…∞.3.3.3
Многогранник
Мозаика

Квадратная бипирамида[править | править код]

Семейство бипирамид

Конфигурация	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	…V∞.4.4
Многогранник
Мозаика

См. также[править | править код]

Граф октаэдра
Звёздчатый октаэдр
Координационная теория
Октаэдральная симметрия^[en]
Октаэдральное число
Ромбоусечённый додекаэдр
Триакисоктаэдр
Усечённый октаэдр
Центрированное октаэдральное число^[en]

Примечания[править | править код]

↑ Селиванов Д. Ф.,. Тело геометрическое // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
↑ Finbow, Hartnell, Nowakowski, Plummer, 2010, с. 894–912.
↑ ¹ ² ³ Weisstein, Eric W. Octahedron (англ.) на сайте Wolfram MathWorld.
↑ Steven Dutch. Enumeration of Polyhedra. Дата обращения: 8 ноября 2015. Архивировано из оригинала 10 октября 2011 года.
↑ Counting polyhedra. Дата обращения: 8 ноября 2015. Архивировано 6 мая 2016 года.
↑ Архивированная копия. Дата обращения: 14 августа 2016. Архивировано 17 ноября 2014 года.
↑ Смольянинов Н. А. Практическое руководство по минералогии. — 2-е изд., испр. и доп. — М.: Недра, 1972. — С. 39. — 27 000 экз.
↑ Klein, 2002, с. 633–649.
↑ Williams, 1979.
↑ Two Dimensional symmetry Mutations by Daniel Huson

Литература[править | править код]

Большая советская энциклопедия
Arthur S. Finbow, Bert L. Hartnell, Richard J. Nowakowski, Michael D. Plummer. On well-covered triangulations. III // Discrete Applied Mathematics. — 2010. — Т. 158, вып. 8. — doi:10.1016/j.dam.2009.08.002.
Douglas J. Klein. Resistance-Distance Sum Rules // Croatica Chemica Acta. — 2002. — Т. 75, вып. 2. Архивировано 10 июня 2007 года.
R. Williams. Chapter 5 The Kaleidoscope, Section: 5.7 Wythoff’s // The Geometrical Foundation of Natural Structure: A Source Book of Design. — New York: Dover Publications, 1979.

Ссылки[править | править код]

Weisstein, Eric W. Octahedron (англ.) на сайте Wolfram MathWorld.
Klitzing Polytopes, 3D convex uniform polyhedra
Editable printable net of an octahedron with interactive 3D view
Paper model of the octahedron
K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
The Uniform Polyhedra
Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Conway Notation for Polyhedra Try: dP4

Источник

Октаэдр и площадь полной его поверхности: описание, формулы, примеры

Содержание:

Что такое октаэдр

Свойства октаэдра

Математические характеристики тела

Как вычислить площадь поверхности октаэдра

Как вычислить объём правильного октаэдра

Развёртка

Октаэдр.

Свойства октаэдра.

Развёртка октаэдра.

Симметрия октаэдра.

Октаэдр

Математические характеристики октаэдра

Вариант развертки

Видео. Октаэдр из набора “Волшебные грани”

Видео. Вращение правильных многогранников

Октаэдр

Математические характеристики октаэдра

Популярное

Правильный октаэдр[править | править код]

Размеры[править | править код]

Ортогональные проекции[править | править код]

Сферическая мозаика[править | править код]

Декартовы координаты[править | править код]

Площадь и объём[править | править код]

Геометрические связи[править | править код]

Однородное раскрашивание и симметрия[править | править код]

Развёртки[править | править код]

Двойственность[править | править код]

Огранка[править | править код]

Неправильные октаэдры[править | править код]

Другие выпуклые восьмигранники[править | править код]

Октаэдры в физическом мире[править | править код]

Октаэдры в природе[править | править код]

Октаэдры в искусстве и культуре[править | править код]

Тетраэдральная связка[править | править код]

Связанные многогранники[править | править код]

Тетратетраэдр[править | править код]

Треугольная антипризма[править | править код]

Квадратная бипирамида[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Вам также может понравиться

Как составить акт на неисправное оборудование

Коэффициент сравнения как найти

Как найти аудиторию для мероприятия

Добавить комментарий Отменить ответ