Как найти площадь основания пирамиды равнобедренный треугольник

Основание правильной пирамиды является правильный многоугольник – равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды – это площадь этой плоской фигуры.

Площадь основания правильной пирамиды

Правильная пирамида может быть трех видов:

• треугольная,
• четырехугольная,
• шестиугольная.

Соответственно у правильной треугольной пирамида основание – равносторонний треугольник. У правильной четырехугольной пирамиды основание – квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды:

Площадь основания правильной треугольной пирамиды

В основании равносторонний треугольник – находим его площадь:

, где – сторона треугольника.

Площадь основания правильной четырехугольной пирамиды

В основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:

, где – сторона квадрата.

Площадь основания правильной шестиугольной пирамиды

Это площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле:

Площадь основания любой пирамиды

Площадь основания любой пирамиды – это площадь ее основания.

Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье “Площадь треугольника”.

В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах.

Теперь давайте решим несколько задач для нахождения площади основания пирамиды

Примеры решения задач

Задача 1

Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.

Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона , тогда

Ответ:

Задача 2

Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5 м². Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?

Решение:

Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны . Получим: м².

Теперь подсчитаем, сколько нам понадобится досок: .

Ответ: 108 досок.

Задача 3

Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.

Решение: иными словами – нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой – высотой. Определяем площадь по формуле:

.

Ответ: 8

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.

Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.

• Формула площади правильной пирамиды
  • 1. Общая формула

  • 2. Площадь правильной треугольной пирамиды

  • 3. Площадь правильной четырехугольной пирамиды

  • 4. Площадь правильной шестиугольной пирамиды

Формула площади правильной пирамиды

1. Общая формула

Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.

S_полн. = S_бок. + S_осн.

Боковой гранью правильной пирамиды является равнобедренный треугольник.

Площадь треугольника вычисляется по формулам:

1. Через длину основания (a) и высоту (h):

2. Через основание (a) и боковую сторону (b):

Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.

2. Площадь правильной треугольной пирамиды

Основание: равносторонний треугольник.

L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.

3. Площадь правильной четырехугольной пирамиды

Основание: квадрат.

Площадь	Формула
основание	Sосн. = a2
боковая поверхность	Sбок. = 2aL
полная	Sполн. = a2 + 2aL

microexcel.ru

4. Площадь правильной шестиугольной пирамиды

Основание: правильный шестиугольник

При подготовке к ЕГЭ по математике учащимся приходится систематизировать знания по алгебре и геометрии. Хочется объединить все известные сведения, например, о том, как вычислить площадь пирамиды. Причем начиная от основания и боковых граней до площади всей поверхности. Если с боковыми гранями ситуация ясна, так как они являются треугольниками, то основание всегда разное.

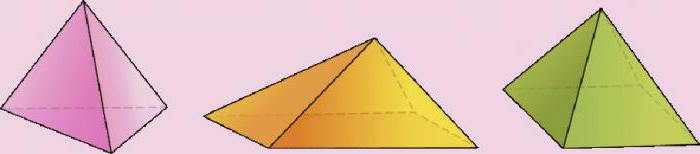
Как быть при нахождении площади основания пирамиды?

Оно может быть совершенно любой фигурой: от произвольного треугольника до n-угольника. И это основание, кроме различия в количестве углов, может являться правильной фигурой или неправильной. В интересующих школьников заданиях по ЕГЭ встречаются только задания с правильными фигурами в основании. Поэтому речь будет идти только о них.

Правильный треугольник

То есть равносторонний. Тот, у которого все стороны равны и обозначены буквой «а». В этом случае площадь основания пирамиды вычисляется по формуле:

S = (а² * √3) / 4.

Квадрат

Формула для вычисления его площади самая простая, здесь «а» – снова сторона:

S = а².

Произвольный правильный n-угольник

У стороны многоугольника то же обозначение. Для количества углов используется латинская буква n.

S = (n * а²) / (4 * tg (180º/n)).

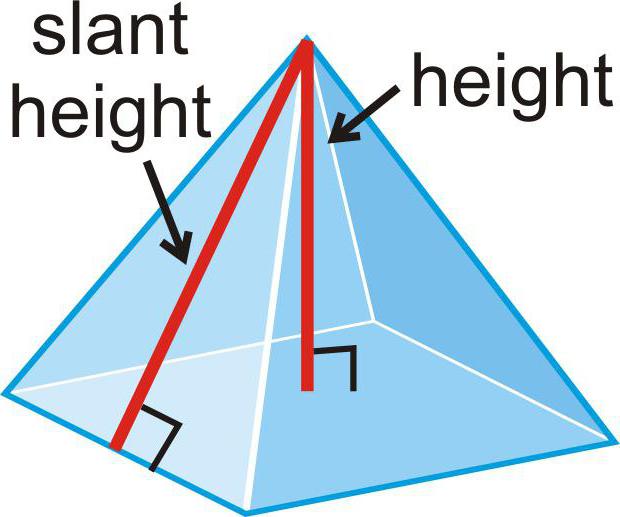
Как поступить при вычислении площади боковой и полной поверхности?

Поскольку в основании лежит правильная фигура, то все грани пирамиды оказываются равными. Причем каждая из них является равнобедренным треугольником, поскольку боковые ребра равны. Тогда для того, чтобы вычислить боковую площадь пирамиды, потребуется формула, состоящая из суммы одинаковых одночленов. Число слагаемых определяется количеством сторон основания.

Площадь равнобедренного треугольника вычисляется по формуле, в которой половина произведения основания умножается на высоту. Эта высота в пирамиде называется апофемой. Ее обозначение – «А». Общая формула для площади боковой поверхности выглядит так:

S = ½ Р*А, где Р — периметр основания пирамиды.

Бывают ситуации, когда не известны стороны основания, но даны боковые ребра (в) и плоский угол при ее вершине (α). Тогда полагается использовать такую формулу, чтобы вычислить боковую площадь пирамиды:

S = n/2 * в² sin α.

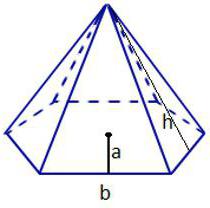
Задача № 1

Условие. Найти общую площадь пирамиды, если в его основании лежит равносторонний треугольник со стороной 4 см, а апофема имеет значение √3 см.

Решение. Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см².

Для треугольника в основании получится такое значение площади: (4²*√3) / 4 = 4√3 см².

Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см².

Ответ. 10√3 см².

Задача № 2

Условие. Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.

Решение. Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.

Первые расчеты просты и приводят к такому числу: 49 мм². Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16)²) = √2985,9375 = 54,644 мм². Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.

Получается: 49 + 4*54,644 = 267,576 мм².

Ответ. Искомое значение 267,576 мм².

Задача № 3

Условие. У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.

Решение. Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.

Придется вспомнить теорему Пифагора и рассмотреть прямоугольный треугольник. Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.

Искомая апофема (гипотенуза прямоугольного треугольника) равна √(3² + 4²) = 5 (см).

Теперь можно вычислять искомую величину: ½*(4*6)*5+6² = 96 (см²).

Ответ. 96 см².

Задача № 4

Условие. Дана правильная шестиугольная пирамида. Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?

Решение. Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.

Первым делом вычисляется площадь основания по указанной выше формуле: (6*22²) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см².

Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.

Расчеты по формуле Герона: √(72*(72-22)*(72-61)²)=√435600=660 см². Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см². Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см².

Ответ. Основания – 726√3 см², боковой поверхности – 3960 см², вся площадь – 5217 см².

Площадь основания пирамиды

Основание правильной пирамиды является правильный многоугольник — равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды — это площадь этой плоской фигуры.

Площадь основания правильной пирамиды

Правильная пирамида может быть трех видов:

• треугольная,
• четырехугольная,
• шестиугольная.

Соответственно у правильной треугольной пирамида основание — равносторонний треугольник. У правильной четырехугольной пирамиды основание — квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды:

Площадь основания правильной треугольной пирамиды

В основании равносторонний треугольник — находим его площадь:

, где — сторона треугольника.

Основание треугольной пирамиды

Площадь основания правильной четырехугольной пирамиды

В основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:

, где — сторона квадрата.

Основание четырехугольной пирамиды

Площадь основания правильной шестиугольной пирамиды

Это площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле:

Основание шестиугольной пирамиды

Площадь основания любой пирамиды

Площадь основания любой пирамиды — это площадь ее основания.

Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье «Площадь треугольника».

В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах.

Теперь давайте решим несколько задач для нахождения площади основания пирамиды

Примеры решения задач

Задача 1

Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.

Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона , тогда

Ответ:

Задача 2

Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5 м 2 . Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?

Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны . Получим: м 2 .

Теперь подсчитаем, сколько нам понадобится досок: .

Задача 3

Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.

Решение: иными словами — нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой — высотой. Определяем площадь по формуле:

.

Нахождение площади правильной пирамиды: формулы

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.

Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.

Формула площади правильной пирамиды

1. Общая формула

Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.

Боковой гранью правильной пирамиды является равнобедренный треугольник.

Площадь треугольника вычисляется по формулам:

1. Через длину основания (a) и высоту (h):

2. Через основание (a) и боковую сторону (b):

Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.

2. Площадь правильной треугольной пирамиды

Основание: равносторонний треугольник.

Треугольная пирамида и формулы для определения ее площади

Пирамида – геометрическая пространственная фигура, характеристики которой изучают в старших классах школы в курсе стереометрии. В данной статье рассмотрим треугольную пирамиду, ее виды, а также формулы для расчета площади ее поверхности.

О какой пирамиде пойдет речь?

Треугольная пирамида представляет собой фигуру, которую можно получить, если соединить все вершины произвольного треугольника с одной единственной точкой, не лежащей в плоскости этого треугольника. Согласно этому определению рассматриваемая пирамида должна состоять из исходного треугольника, который называется основанием фигуры, и трех боковых треугольников, которые имеют по одной общей стороне с основанием и соединены друг с другом в точке. Последняя называется вершиной пирамиды.

Вам будет интересно: Защита проекта: образец. Темы для защиты проекта. Требования к проектной работе

Рисунок выше демонстрирует произвольную треугольную пирамиду.

Рассматриваемая фигура может быть наклонной или прямой. В последнем случае перпендикуляр, опущенный из вершины пирамиды на ее основание, должен его пересекать в геометрическом центре. Геометрическим центром любого треугольника является точка пересечения его медиан. Геометрический центр совпадает с центром масс фигуры в физике.

Если в основании прямой пирамиды будет лежать правильный (равносторонний) треугольник, то она называется правильной треугольной. В правильной пирамиде все боковые стороны равны друг другу и представляют собой равносторонние треугольники.

Если высота правильной пирамиды такова, что ее боковые треугольники становятся равносторонними, то она называется тетраэдром. В тетраэдре все четыре грани равны друг другу, поэтому каждая из них может полагаться основанием.

Элементы пирамиды

К этим элементам относятся грани или стороны фигуры, ее ребра, вершины, высота и апофемы.

Как было показано, все стороны треугольной пирамиды являются треугольниками. Их число равно 4 (3 боковых и один в основании).

Вершины – это точки пересечения трех треугольных сторон. Не сложно догадаться, что для рассматриваемой пирамиды их 4 (3 принадлежат основанию и 1 – вершина пирамиды).

Ребра можно определить, как линии пересечения двух треугольных сторон, или как линии, которые соединяют каждые две вершины. Количество ребер соответствует удвоенному числу вершин основания, то есть для треугольной пирамиды оно равно 6 (3 ребра принадлежат основанию и 3 ребра образованы боковыми гранями).

Высота, как выше было отмечено, является длиной перпендикуляра, проведенного из вершины пирамиды к ее основанию. Если из этой вершины провести высоты к каждой из сторон треугольного основания, то они будут называться апотемами (или апофемами). Таким образом, пирамида треугольная имеет одну высоту и три апофемы. Последние равны друг другу для правильной пирамиды.

Основание пирамиды и его площадь

Поскольку основание для рассматриваемой фигуры в общем случае представляет собой треугольник, то для расчета его площади достаточно найти его высоту ho и длину стороны основания a, на которую она опущена. Формула для площади So основания имеет вид:

Если треугольник основания является равносторонним, тогда площадь основания треугольной пирамиды вычисляется по такой формуле:

То есть площадь So однозначно определяется длиной стороны a треугольного основания.

Боковая и общая площадь фигуры

Прежде чем рассматривать площадь треугольной пирамиды, полезно привести ее развертку. Она изображена на рисунке ниже.

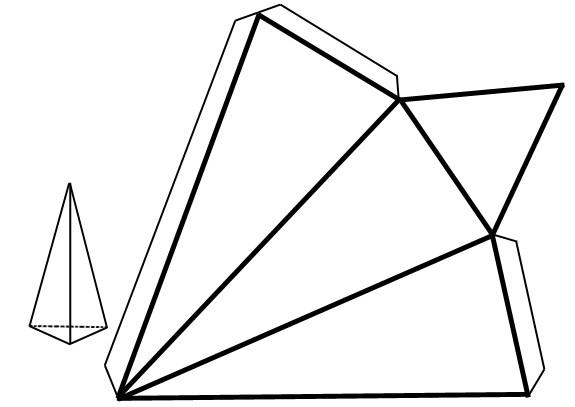
Площадь этой развертки, образованной четырьмя треугольниками, является общей площадью пирамиды. Один из треугольников соответствует основанию, формула для рассматриваемой величины которого была записана выше. Три боковых треугольных грани в сумме образуют боковую площадь фигуры. Поэтому для определения этой величины достаточно к каждому из них применить записанную выше формулу для произвольного треугольника, а затем, сложить три полученных результата.

Если пирамида является правильной, то расчет площади боковой поверхности облегчается, поскольку все грани боковые представляют собой одинаковые равносторонние треугольники. Обозначим hb длину апотемы, тогда площадь боковой поверхности Sb можно определить так:

Эта формула следует из общего выражения для площади треугольника. Цифра 3 появилась в числители из-за того, что пирамида имеет три боковых грани.

Апотему hb в правильной пирамиде можно вычислить, если известна высота фигуры h. Применяя теорему Пифагора, получаем:

Очевидно, что общая площадь S поверхности фигуры равна сумме ее площадей боковой поверхности и основания:

Для правильной пирамиды, подставляя все известные величины, получаем формулу:

S = √3/4*a2 + 3/2*a*√(h2 + a2/12)

Площадь пирамиды треугольной зависит только от длины стороны ее основания и от высоты.

Пример задачи

Известно, что боковое ребро треугольной пирамиды равно 7 см, а сторона основания составляет 5 см. Необходимо найти площадь поверхности фигуры, если известно, что пирамида является правильной.

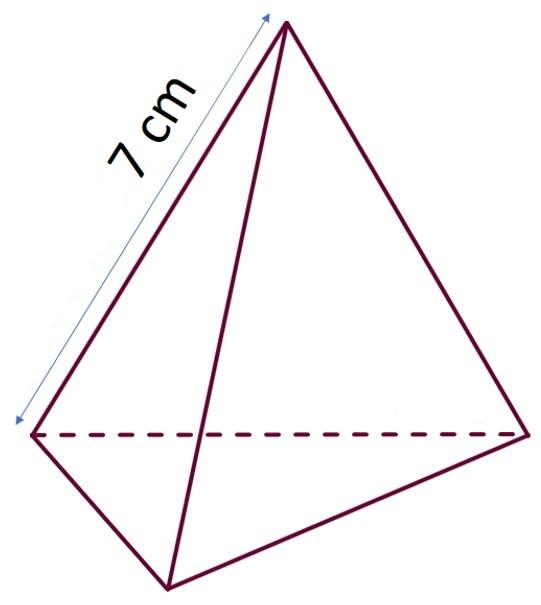
Воспользуемся равенством общего вида:

Площадь So равна:

So = √3/4*a2 = √3/4*52 ≈ 10,825 см2.

Для определения площади боковой поверхности, необходимо найти апотему. Не сложно показать, что через длину бокового ребра ab она определяется по формуле:

hb = √(ab2 – a2/4) = √(7 2 – 52/4) ≈ 6,538 см.

Тогда площадь Sb равна:

Sb = 3/2*a*hb = 3/2*5*6,538 = 49,035 см2.

Общая площадь пирамиды составляет:

S = So + Sb = 10,825 + 49,035 = 59,86 см2.

Заметим, что при решении задачи мы не использовали в расчетах значение высоты пирамиды.

[spoiler title=”источники:”]

http://1ku.ru/obrazovanie/40981-treugolnaja-piramida-i-formuly-dlja-opredelenija-ee-ploshhadi/

[/spoiler]

Задача.

В основании пирамиды лежит равнобедренный треугольник с боковой стороной b и углом при основании β. все боковые грани образуют с основанием угол φ.

Решение.

Поскольку в основании пирамиды лежит равнобедренный треугольник, то для нахождения площади равнобедренного треугольника, воспользуемся приведенными в соответствующем уроке формулами.

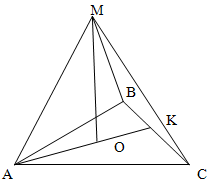
При желании можно разбить треугольник ABC на два прямоугольных треугольника AKB и AKC. Но в результате формулы будут все равно тождественны. Действительно,

AK = AB sin ß = b sin β

BK = AB cos β = b cos β

S_ABK = AK * BK / 2 = b²sin β cos β / 2

откуда

S_ABС =   2S_ABK =   b²sin β cos β 

(примем за искомую площадь основания, далее справочно приведем к той же формуле, которая указана по ссылке выше)

Если воспользоваться основными тригонометрическими тождествами, то

b²sin β cos β = 1/2 b²sin 2β = 1/2 b²sin 2β  

или как по основной формуле (площади равнобедренного треугольника)

1/2 b²sin 2β = 1/2 b²sin (180 – α)  =  1/2 b²sin α

Теперь найдем площадь боковой поверхности пирамиды.

Сначала найдем высоту боковых граней, прилежащих к равным сторонам равнобедренного треугольника, лежащего в основании пирамиды. При этом учтем, что высота пирамиды проецируется в точку О основания, которая одновременно является центром вписанной окружности. Вместе с радиусом вписанной окружности, высота боковой грани образует прямоугольный треугольник. Откуда высота боковой грани пирамиды равна:

h = r / sin φ

Длину радиуса вписанной окружности найдем как

r = S/p

Учитывая, что BC = 2BK, то BC = 2b cos β

откуда

p = ( b + b + 2b cos β ) / 2

p = ( 2b + 2b cos β ) / 2

p = 2b ( 1 + cos β ) / 2

p = b ( 1 + cos β )

Таким образом, радиус вписанной окружности в основание пирамиды будет равен

r = S / p

r = b²sin β cos β / b ( 1 + cos β ) = b sin β cos β / ( 1 + cos β )

Теперь определим высоту боковых граней пирамиды. Зная, что

l / r = cos φ, то

l = r cos φ

Тогда площадь грани пирамиды, прилегающей к равным сторонам основания (а в основании пирамиды у нас лежит равнобедренный треугольник) будет равна:

S1 = lb / 2

S1 = r cos φ * b / 2

S1 = b sin β cos β / ( 1 + cos β ) cos φ * b / 2

S1 = b² sin β cos β / ( 1 + cos β ) cos φ / 2

S1 = b² sin β cos β  cos φ / ( 2 ( 1 + cos β ) )

Площадь боковой грани, прилегающей к основанию, равна:

S2 = BC * l / 2

S2 = 2b cos β *  r cos φ / 2

S2 = b cos β * r cos φ

S2 = b cos β * b sin β cos β / ( 1 + cos β ) * cos φ

S2 = b² cos² β sin β cos φ / ( 1 + cos β )

Площадь боковой поверхности пирамиды равна:

Sбок = 2S1 + S2

Sбок = 2 * b² sin β cos β / ( 2 ( 1 + cos β ) cos φ ) + b² cos² β sin β cos φ / ( 1 + cos β )

Sбок = b² sin β cos β cos φ / ( 1 + cos β ) + b² cos² β sin β cos φ / ( 1 + cos β )

Sбок = ( b² sin β cos β cos φ + b² cos² β sin β cos φ ) / ( 1 + cos β )

Sбок = b² sin β cos β cos φ ( 1  + cos β ) / ( 1 + cos β )

Sбок = b² sin β cos β cos φ

Откуда площадь полной поверхности пирамиды с равнобедренным треугольником в основании составит:

S = Sбок + Sосн

S = b² sin β cos β cos φ + b² cos² β sin β cos φ / ( 1 + cos β )

0
 

 Пирамида с прямоугольным треугольником в основании |

Описание курса

| Правильная треугольная пирамида (правильная пирамида с треугольником в основании). Тетраэдр