Как найти площадь основания пирамиды все формулы

Как найти площадь основания пирамиды все формулы

Основание правильной пирамиды является правильный многоугольник – равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды – это площадь этой плоской фигуры.

Площадь основания правильной пирамиды

Правильная пирамида может быть трех видов:

  • треугольная,
  • четырехугольная,
  • шестиугольная.

Соответственно у правильной треугольной пирамида основание – равносторонний треугольник. У правильной четырехугольной пирамиды основание – квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды:

Площадь основания правильной треугольной пирамиды

В основании равносторонний треугольник – находим его площадь:

displaystyle S=frac{a^2 sqrt{3}}{4}, где a – сторона треугольника.

Основание треугольной пирамиды

Основание треугольной пирамиды

Площадь основания правильной четырехугольной пирамиды

В основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:

displaystyle S=a^2, где a – сторона квадрата.

Основание четырехугольной пирамиды

Основание четырехугольной пирамиды

Площадь основания правильной шестиугольной пирамиды

Это площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле:

displaystyle S=frac{3a^2 sqrt{3}}{2}

Основание шестиугольной пирамиды

Основание шестиугольной пирамиды

Площадь основания любой пирамиды

Площадь основания любой пирамиды – это площадь ее основания.

Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье “Площадь треугольника”.

В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах.

Теперь давайте решим несколько задач для нахождения площади основания пирамиды

Примеры решения задач

Задача 1

Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.

Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: S=frac{a^2 sqrt{3}}{4}. Нам дана сторона a=2, тогда S=frac{2^2 sqrt{3}}{4} = sqrt{3}

Ответ: sqrt{3}

Задача 2

Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5sqrt{3} м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?

Решение:

Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: S=frac{3a^2 sqrt{3}}{2}. Подставим в нее значение стороны a=6. Получим: S=frac{3 cdot 6^2 sqrt{3}}{2}=54 sqrt{3} м2.

Теперь подсчитаем, сколько нам понадобится досок: N=frac{54 sqrt{3}}{0,5 sqrt{3}}=108.

Ответ: 108 досок.

Задача 3

Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.

Площадь основания пирамиды - к задаче 3

Решение: иными словами – нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой – высотой. Определяем площадь по формуле:

S=frac{a^2}{2}=frac{4^2}{2}=8.

Ответ: 8

Источник

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.

Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.

  • Формула площади правильной пирамиды

    • 1. Общая формула

    • 2. Площадь правильной треугольной пирамиды

    • 3. Площадь правильной четырехугольной пирамиды

    • 4. Площадь правильной шестиугольной пирамиды

Формула площади правильной пирамиды

Формула площади поверхности правильной пирамиды

1. Общая формула

Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.

Sполн. = Sбок. + Sосн.

Боковой гранью правильной пирамиды является равнобедренный треугольник.

Нахождение площади правильной пирамиды: формулы

Площадь треугольника вычисляется по формулам:

1. Через длину основания (a) и высоту (h):

Формула площади треугольника

2. Через основание (a) и боковую сторону (b):

Формула площади равнобедренного треугольника

Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.

2. Площадь правильной треугольной пирамиды

2. Площадь правильной треугольной пирамиды

Основание: равносторонний треугольник.

L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.

3. Площадь правильной четырехугольной пирамиды

Площадь правильной четырехугольной пирамиды

Основание: квадрат.
Площадь Формула
основание Sосн. = a2
боковая поверхность Sбок. = 2aL
Нахождение площади правильной пирамиды: формулы
полная Sполн. = a2 + 2aL
Нахождение площади правильной пирамиды: формулы

microexcel.ru

4. Площадь правильной шестиугольной пирамиды

Площадь поверхности правильной шестиугольной пирамиды

Основание: правильный шестиугольник

Источник

Вычисление площади правильной треугольной пирамиды

Определение

Правильная треугольная пирамида (тетраэдр) — это многогранник, в основании которого лежит правильный треугольник со сторонами a и боковыми гранями в виде равнобедренных треугольников с основанием a и сторонами b.

Треугольник

 

Площадь поверхности такой фигуры складывается из площадей основания многогранника и трех боковых граней. В записи на математический язык это выглядит так:

((1);S=S_{осн}+3times S_{бок})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Нахождение площади основания пирамиды

Поскольку правильный тетраэдр основан на треугольнике, для определения площади основания рассматриваемого многогранника воспользуемся формулой нахождения площади треугольника:

(S=frac12ah)

Значение переменных: a — длина стороны равностороннего треугольника, h — его высота.

Далее произведем подстановку формулы вычисления высоты правильного треугольника и получим искомое выражение:

((2);S_{осн}=frac{sqrt3}4a^2)

Вычисление площади боковых граней и полной поверхности

Боковые грани правильной треугольной пирамиды представлены тремя равнобедренными треугольниками. Выведем формулу расчета площади каждого из них из классического способа вычисления площади треугольника:

(S=frac12ah)

Здесь переменная a обозначает основание треугольника, h — его высоту.

Теперь выполним подстановку выражения, с помощью которого находится высота треугольника с одинаковыми бедрами, и получим уравнение определения площади равнобедренного треугольника:

((3);S_{бок}=frac{asqrt{b^2-frac{a^2}4}}2)

В этом случае b — это боковые ребра треугольника, равные между собой.

Подставим в выражение (1) формулы (2) и (3) и получим уравнение, с помощью которого рассчитывается площадь полной поверхности правильного тетраэдра:

(S=frac{sqrt3}4a^2+frac32times asqrt{b^2-frac{a^2}4})

Примеры задач с решением

Задача

Дано

Правильный тетраэдр MABC с вершиной М. Высота основания AK=3 см.

∠MAB=∠MAC=∠MBA=∠MBC=∠MAB=∠MCA=∠MCB=45°. Необходимо вычислить площадь пирамиды MABC.

Задача

 

Решение

В основании правильного тетраэдра лежит равносторонний треугольник с известной длиной высоты. Применим свойство правильного треугольника, состоящее в следующем:

(h=frac{sqrt3}2a)

Преобразуем данное выражение так, чтобы вывести формулу стороны a:

(a=frac h{frac{sqrt3}2})

Теперь найдем a:

(a=frac3{frac{sqrt3}2}=frac{3times2}{sqrt3}=frac6{sqrt3})

Подставим полученное выражение в формулу нахождения площади основания правильного многогранника с тремя боковыми гранями:

(S_{осн}=frac{sqrt3}4timesleft(frac6{sqrt3}right)^2=frac{sqrt3}4timesfrac{6^2}{sqrt3^2}=frac{36sqrt3}{4times3}=3sqrt3)

Далее необходимо найти площадь боковых граней тетраэдра. Для этого произведем вычисление высоты MK. Так как угол между гранью и основанием пирамиды равен 45°, то ∠OKM=45°, следовательно:

(frac{OK}{MK}=cosleft(45^circright)=frac{sqrt2}2)

По свойству правильного треугольника, отрезок OK равен радиусу вписанной в ΔABC окружности.

Найдем ее по соответствующей формуле:

(OK=r=frac{sqrt3}6a=frac{sqrt3}6timesfrac6{sqrt3}=frac{6sqrt3}{6sqrt3}=1)

Подставим найденную величину в отношение ОК к МК:

(frac{OK}{MK}=frac{sqrt2}2)

(frac1{MK}=frac{sqrt2}2)

Из данной пропорции выведем выражение, по которому можно определить длину высоты MK:

(MK=frac2{sqrt2})

Теперь, когда известны основание и высота равнобедренного треугольника, составляющего боковую грань пирамиды MABC, подставим значения в классическую формулу нахождения площади треугольника:

(S_{бок}=frac12ah=frac12timesfrac6{sqrt3}timesfrac2{sqrt2}=frac{1times6times2}{2timessqrt3timessqrt2}=frac{12}{2sqrt6}=frac6{sqrt6})

Суммируем площадь основания и боковых граней пирамиды:

(S_{MABC}=3sqrt3+3times6sqrt6=3sqrt3+18sqrt6)

Ответ, выраженный в квадратных сантиметрах: (3sqrt3+18sqrt6;(см^2))

Источник

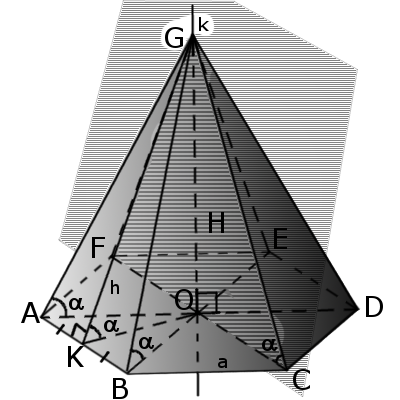
Пирамида. Формулы и свойства пирамиды

Определение.

Пирамида — это многогранная объемная фигура, ограниченная плоским многоугольником (основой) и треугольниками, имеющих общую вершину, не лежащую в плоскости основания.

Изображение пирамиды с обозначениями
Рис.1

Определение. Боковая грань – это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).

Определение. Боковые ребра – это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.

Определение. Высота пирамиды – это перпендикуляр, опущенный из вершины на основание пирамиды.

Определение. Апофема – это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.

Определение. Диагональное сечение – это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.

Определение. Правильная пирамида – это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.

Объём и площадь поверхности пирамиды

Формула. Объём пирамиды через площадь основы и высоту:

Определение. Боковая поверхность пирамиды – это совокупная площадь всех боковых граней пирамиды.

Определение. Полная поверхность пирамиды – это совокупность площадей боковой поверхности и площади основания пирамиды.

Формула. Площадь боковой поверхности правильной пирамиды через периметр основания и апофему:

Свойства пирамиды

Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).

Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.

Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.

Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.

Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.

Свойства правильной пирамиды

1. Вершина пирамиды равноудалена от всех углов основания.

2. Все боковые ребра равны.

3. Все боковые ребра наклонены под одинаковыми углами к основанию.

4. Апофемы всех боковых граней равны.

5. Площади всех боковых граней равны.

6. Все грани имеют одинаковые двугранные (плоские) углы.

7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.

8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.

9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n, где n – это количество углов в основании пирамиды.

Связь пирамиды со сферой

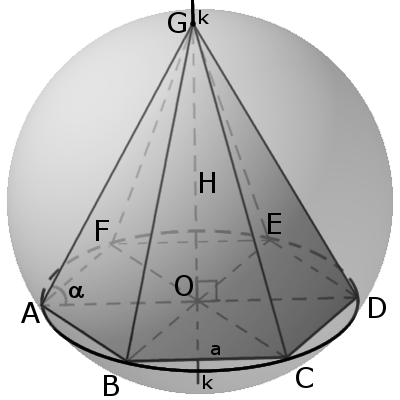
Пример вписанной пирамиды в сферу

Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.

Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.

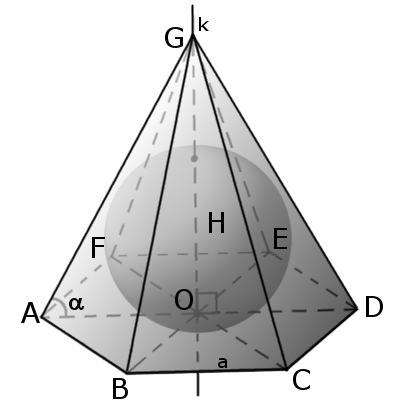
Пример описаной пирамиды вокруг сфери

В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.

Связь пирамиды с конусом

Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.

Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.

Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.

Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.

Связь пирамиды с цилиндром

Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.

Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.

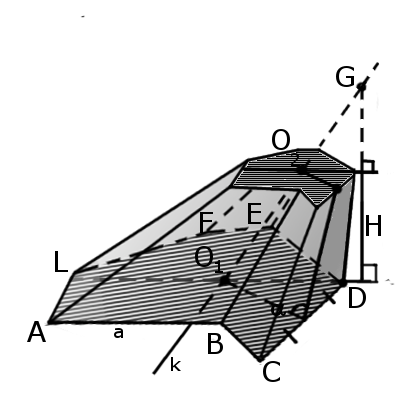
Приклад зрізаної пирамиды

Определение. Усеченная пирамида (пирамидальная призма) – это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции.

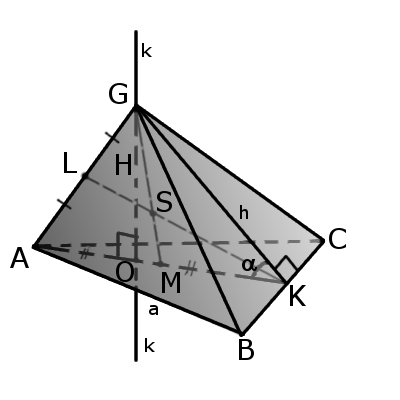
Пример треугольной пирамиди

Определение. Треугольная пирамида (четырехгранник) – это пирамида в которой три грани и основание являются произвольными треугольниками.

В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.

Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол.

Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).

Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).

Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.

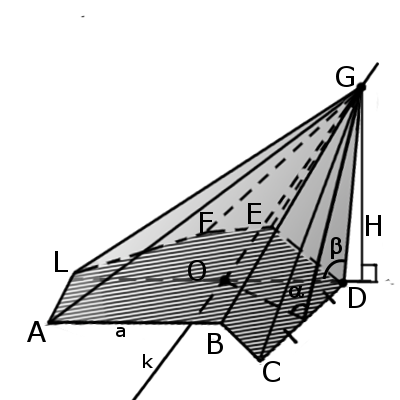
Пример наклонной пирамиди

Определение. Наклонная пирамида – это пирамида в которой одно из ребер образует тупой угол (β) с основанием.

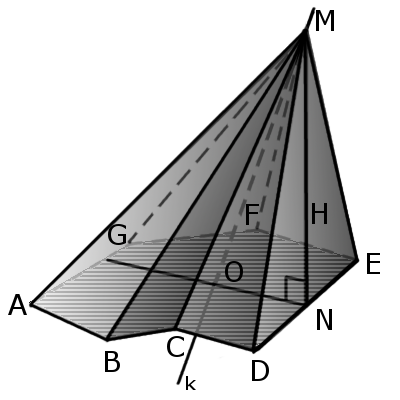
Пример прямоугольной пирамиды

Определение. Прямоугольная пирамида – это пирамида в которой одна из боковых граней перпендикулярна к основанию.

Определение. Остроугольная пирамида – это пирамида в которой апофема больше половины длины стороны основания.

Определение. Тупоугольная пирамида – это пирамида в которой апофема меньше половины длины стороны основания.

Определение. Правильный тетраэдр – четырехгранник у которого все четыре грани – равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.

Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.

Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание – правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.

Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.

Определение. Звездная пирамида называется многогранник у которого основой является звезда.

Пример бипирамиды

Определение. Бипирамида – многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.

Источник

Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту

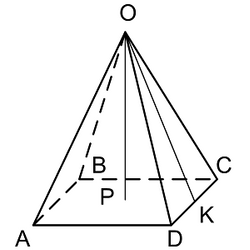
Формулы пирамиды

Для расчёта всех основных параметров пирамиды воспользуйтесь калькулятором.

Свойства правильной пирамиды

  • Боковые ребра правильной пирамиды равны между собой
  • Боковые грани правильной пирамиды равны между собой и являются равнобедренными треугольниками
  • Апофемы правильной пирамиды равны
  • В любую правильную пирамиду можно вписать и описать около неё сферу
  • Все боковые грани образуют с плоскостью основания правильной пирамиды равные углы

Площадь основания правильной пирамиды

$$
S_{осн} = {N * AB^2 over 4 * tan(180/N)}
$$

Где: N – количество сторон у основания пирамиды

Апофема правильной пирамиды

$$
OK = sqrt{OP^2 + ({AB over 2 * tan(180/N)})^2}
$$

Где: N – количество сторон у основания пирамиды

Боковое ребро правильной пирамиды

$$
OD = sqrt{OP^2 + ({AB over 2 * sin(180/N)})^2}
$$

Где: N – количество сторон у основания пирамиды

Объём пирамиды через площадь основы (Sосн) и высоту (OP)

$$
V = {1 over 3} * S_{осн} * OP
$$

Площадь боковой поверхности правильной пирамиды через периметр основания (Pосн) и апофему (OK)

$$
S_Б = {1 over 2} * P_{осн} * OK
$$

Источник

Добавить комментарий