Как найти площадь основания правильного параллелепипеда

Как найти площадь основания правильного параллелепипеда

Как найти площадь основания параллелепипеда

Основанием параллелепипеда всегда является параллелограмм. Для того чтобы найти площадь основания, вычислите площадь этого параллелограмма. Как частный случай, это может быть прямоугольник или квадрат. Также можно найти площадь основания параллелепипеда, зная его объем и высоту.

Как найти площадь основания параллелепипеда

Вам понадобится

  • Линейка, транспортир, инженерный калькулятор

Инструкция

В общем случае основание параллелепипеда представляет собой параллелограмм. Чтобы найти его площадь, с помощью линейки произведите измерение длин его сторон, а транспортиром измерьте угол между ними. Площадь основания параллелепипеда будет равна произведению этих сторон на синус угла между ними S=a • b • Sin(α).

Чтобы определить площадь основания параллелепипеда другим способом, измерьте одну из сторон основания, затем опустите на нее высоту из вершины, которая лежит напротив этой стороны. Измерьте длину этой высоты. Для получения площади основания найдите площадь параллелограмма, умножив длину стороны на высоту, которая на нее опущена S=a • h.

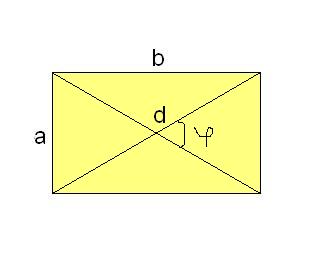
Для получения значения площади другим способом измерьте длины его диагоналей (расстояния между противоположными вершинами), и угол между диагоналями. Площадь будет равна половине произведения диагоналей на синус угла между ними S=0,5•d1•d2•Sin(β).

Для параллелепипеда, в основании которого лежит ромб, достаточно измерить длины его диагоналей и найти половину их произведения S=0,5 • d1 • d2.

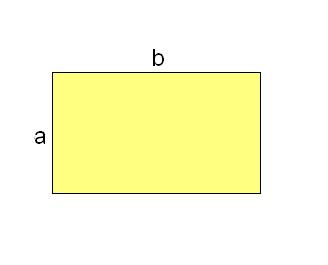
В том случае, когда основание параллелепипеда представляет собой прямоугольник, измерьте длину и ширину этой геометрической фигуры, затем перемножьте эти значения S=a • b. Это и будет площадь его основания. В том случае, когда основание – квадрат, измерьте одну его сторон и возведите во вторую степень S=a².

Если известен объем параллелепипеда, измерьте его высоту. Для этого опустите перпендикуляр из любой вершины верхнего основания на плоскость, к которой принадлежит нижнее основание. Измерьте длину этого отрезка, являющегося высотой параллелепипеда. Если параллелепипед прямой (его боковые ребра перпендикулярны основаниям), достаточно измерить длину одного из этих ребер, которое равно высоте параллелепипеда. Для получения площади основания, объем параллелепипеда поделите на его высоту S=V/h.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Как найти площадь основания параллелепипеда

Основанием параллелепипеда всегда является параллелограмм. Для того чтобы найти площадь основания, вычислите площадь этого параллелограмма. Как частный случай, это может быть прямоугольник или квадрат. Также можно найти площадь основания параллелепипеда, зная его объем и высоту.Как найти площадь основания параллелепипедаВам понадобится

В общем случае основание параллелепипеда представляет собой параллелограмм. Чтобы найти его площадь, с помощью линейки произведите измерениедлин его сторон, а транспортиром измерьте угол между ними. Площадь основания параллелепипеда будет равна произведению этих сторон на синус угла между нимиS=a • b • Sin(α).

Чтобы определить площадь основания параллелепипеда другим способом, измерьте одну из сторон основания, затем опустите на нее высоту из вершины, которая лежит напротив этой стороны. Измерьте длину этой высоты. Для получения площади основания найдите площадь параллелограмма, умножив длину стороны на высоту, которая на нее опущена S=a • h.

Для получения значения площади другим способом измерьте длины его диагоналей (расстояния между противоположными вершинами), и угол между диагоналями. Площадь будет равна половине произведения диагоналей на синус угла между ними S=0,5•d1•d2•Sin(β).

Для параллелепипеда, в основании которого лежит ромб, достаточно измерить длины его диагоналей и найти половину их произведения S=0,5 • d1 • d2.

В том случае, когда основание параллелепипеда представляет собой прямоугольник, измерьте длину и ширину этой геометрической фигуры, затем перемножьте эти значенияS=a • b. Это и будет площадь его основания. В том случае, когда основание – квадрат, измерьте одну его сторон и возведите во вторую степень S=a².

Если известен объем параллелепипеда, измерьте его высоту. Для этого опустите перпендикуляр из любой вершины верхнего основания на плоскость, к которой принадлежит нижнее основание. Измерьте длину этого отрезка, являющегося высотой параллелепипеда. Если параллелепипед прямой (его боковые ребра перпендикулярны основаниям), достаточно измерить длину одного из этих ребер, которое равно высоте параллелепипеда. Для получения площади основания, объем параллелепипеда поделите на его высоту S=V/h.

Источник

Совет 1: Как обнаружить площадь основания параллелепипеда

Основанием параллелепипеда неизменно является параллелограмм. Для того дабы обнаружить площадь основания, вычислите площадь этого параллелограмма. Как частный случай, это может быть прямоугольник либо квадрат. Также дозволено обнаружить площадь основания параллелепипеда , зная его объем и высоту.

Как обнаружить площадь основания параллелепипеда

Вам понадобится

  • Линейка, транспортир, инженерный калькулятор

Инструкция

1. В всеобщем случае основание параллелепипеда представляет собой параллелограмм. Дабы обнаружить его площадь , с подмогой линейки произведите измерение длин его сторон, а транспортиром измерьте угол между ними. Площадь основания параллелепипеда будет равна произведению этих сторон на синус угла между ними S=a • b • Sin(?).

2. Дабы определить площадь основания параллелепипеда иным методом, измерьте одну из сторон основания, после этого опустите на нее высоту из вершины, которая лежит наоборот этой стороны. Измерьте длину этой высоты. Для приобретения площади основания обнаружьте площадь параллелограмма, умножив длину стороны на высоту, которая на нее опущена S=a • h.

3. Для приобретения значения площади иным методом измерьте длины его диагоналей (расстояния между противоположными вершинами), и угол между диагоналями. Площадь будет равна половине произведения диагоналей на синус угла между ними S=0,5•d1•d2•Sin(?).

4. Для параллелепипеда , в основании которого лежит ромб, довольно измерить длины его диагоналей и обнаружить половину их произведения S=0,5 • d1 • d2.

5. В том случае, когда основание параллелепипеда представляет собой прямоугольник, измерьте длину и ширину этой геометрической фигуры, после этого перемножьте эти значения S=a • b. Это и будет площадь его основания. В том случае, когда основание – квадрат, измерьте одну его сторон и возведите во вторую степень S=a?.

6. Если знаменит объем параллелепипеда , измерьте его высоту. Для этого опустите перпендикуляр из всякий вершины верхнего основания на плоскость, к которой принадлежит нижнее основание. Измерьте длину этого отрезка, являющегося высотой параллелепипеда . Если параллелепипед прямой (его боковые ребра перпендикулярны основаниям), довольно измерить длину одного из этих ребер, которое равно высоте параллелепипеда . Для приобретения площади основания, объем параллелепипеда поделите на его высоту S=V/h.

Совет 2: Как находить площадь прямоугольника

Прямоугольник – плоская фигура, состоящая из четырех сторон и четырех прямых углов. Из всех фигур площадь прямоугольника доводится вычислять почаще других. Это и площадь квартиры, и площадь садового участка, и площадь поверхности стола либо полки. Скажем, дабы примитивно оклеить комнату обоями, вычисляют площадь ее прямоугольных стен.

Как находить площадь прямоугольника

Инструкция

1. Самый примитивный метод обнаружить площадь прямоугольника – это перемножить длину прямоугольника на ширину. Таким образом, если длина прямоугольника равна a, а ширина – b, то площадь S = ab.

Как находить <strong>площадь</strong> <b>прямоугольника</b>

2. Нетрудно обнаружить и площадь прямоугольника , зная длину его диагонали и угол между диагоналями. Пускай длина диагонали равна d, а угол между ними – φ. Тогда площадь прямоугольника S = ½d²sinφ.

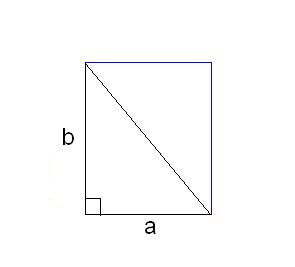
Как находить <strong>площадь</strong> <b>прямоугольника</b>

3. Кстати, из площади прямоугольника дозволено легко вычислить площадь прямоугольного треугольника. Довольно достроить прямоугольный треугольник до прямоугольника так, дабы гипотенуза стала диагональю прямоугольника . Тогда будет видимо, что площадь такого прямоугольника равна произведению катетов треугольника, а площадь самого треугольника, соответственно, равна половине произведения катетов.

Как находить <strong>площадь</strong> <b>прямоугольника</b>

Видео по теме

Источник

Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Рисунок 1

Определение

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.

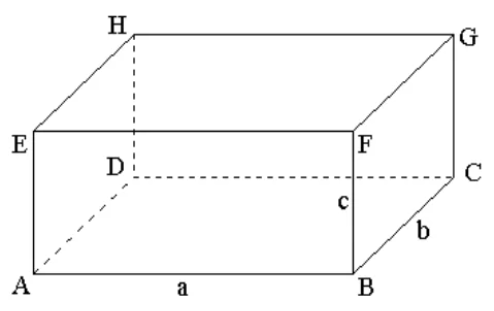
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.

У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.

Рисунок 2

Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.

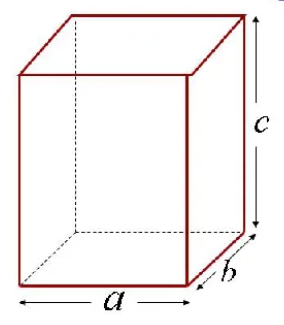
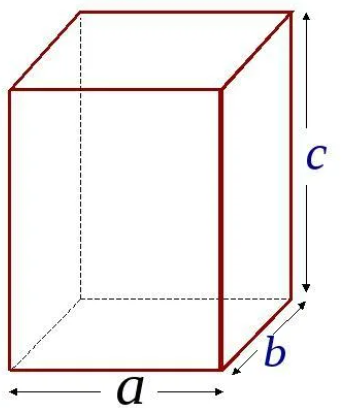
Длина, ширина, высота

Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.

Рисунок 3

Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.

Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.

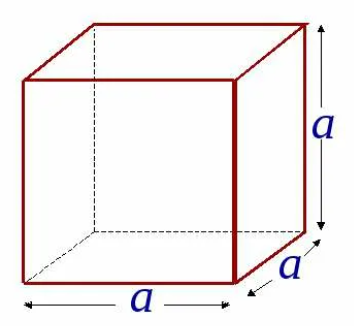
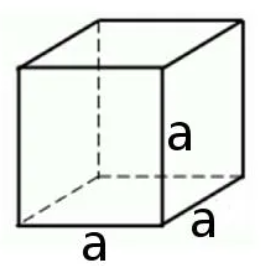
Куб

Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).

Рисунок 4

Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a2. Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a2

Объем прямоугольного параллелепипеда

Рисунок 5

С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.

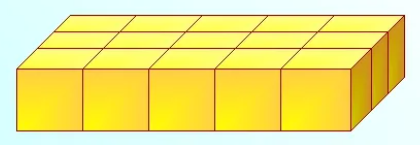
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.

Рисунок 6

 

За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.

Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм3; с ребром 1 см – кубическим сантиметром (см3) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.

Формула объема прямоугольного параллелепипеда

Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.

Рисунок 7

Объем куба

Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:

V=a3

Рисунок 8

Пирамида

Рисунок 9

Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).

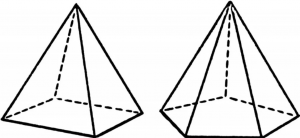
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).

Рисунок 10

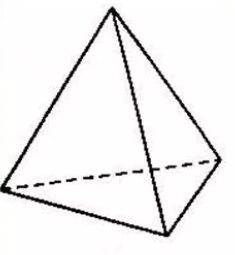
Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.

Рисунок 11

Даниил Романович | Просмотров: 961

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 мая 2022 года; проверки требуют 4 правки.

Параллелепи́пед (др.-греч. παραλληλ-επίπεδον[1] от др.-греч. παρ-άλληλος — «параллельный» и др.-греч. ἐπί-πεδον — «плоскость») — четырёхугольная призма, все грани которой являются параллелограммами.

Типы параллелепипеда[править | править код]

Прямоугольный параллелепипед

Различается несколько типов параллелепипедов:

  • Наклонный — боковые грани не перпендикулярны основанию.
  • Прямой — боковые грани перпендикулярны основанию.
  • Прямоугольный — все грани являются прямоугольниками.
  • Ромбоэдр — все грани являются равными ромбами.
  • Куб — все грани являются квадратами.

Основные элементы[править | править код]

Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.

Свойства[править | править код]

  • Параллелепипед симметричен относительно середины его диагонали.
  • Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
  • Противолежащие грани параллелепипеда параллельны и равны.
  • Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Основные формулы[править | править код]

Прямой параллелепипед[править | править код]

Площадь боковой поверхности
Sб=Ро*h, где Ро — периметр основания, h — высота

Площадь полной поверхности
Sп=Sб+2Sо, где Sо — площадь основания

Объём
V=Sо*h

Прямоугольный параллелепипед[править | править код]

Площадь боковой поверхности
Sб=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда

Площадь полной поверхности
Sп=2(ab+bc+ac)

Объём
V=abc, где a, b, c — измерения прямоугольного параллелепипеда.

Куб[править | править код]

Площадь поверхности: S=6a^{2}

Объём: V=a^{3}, где a — ребро куба.

Произвольный параллелепипед[править | править код]

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения[2]:215.

В математическом анализе[править | править код]

В математическом анализе под n-мерным прямоугольным параллелепипедом B понимают множество точек x=(x_{1},ldots ,x_{n}) вида B={x|a_{1}leqslant x_{1}leqslant b_{1},ldots ,a_{n}leqslant x_{n}leqslant b_{n}}

Сечение параллелепипеда плоскостью[править | править код]

В зависимости от расположения секущей плоскости и параллелепипеда сечение параллелепипеда может быть треугольником, четырехугольником, пятиугольником и шестиугольником.

Примечания[править | править код]

  1. ↑ Древнегреческо-русский словарь Дворецкого «παραλληλεπίπεδον»
  2. ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.

Ссылки[править | править код]

  • Прямоугольный параллелепипед Архивная копия от 21 февраля 2020 на Wayback Machine
Источник

Добавить комментарий