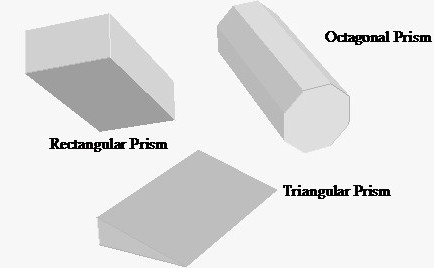
Разные призмы — это не одно и то же. В то же время у них много общего. Чтобы найти площадь основания призмы, нужно выяснить, какой у нее тип.
Содержание
- 1 Общая теория
- 2 Треугольная призма
- 3 Четырехугольная призма
- 4 Правильная пятиугольная призма
- 5 Правильная шестиугольная призма
- 6 Задачи
Общая теория
Призма — это любой многогранник, стороны которого имеют форму параллелограмма. Также у его основания может появиться любой многогранник — от треугольника до n-угольника. Кроме того, основания призм всегда совпадают. Это не касается боковых граней — они могут существенно различаться по размеру.
При устранении неисправностей встречается не только область основания призмы. Может потребоваться знание боковой поверхности, т.е всех граней, не являющихся основанием. Вся поверхность уже будет объединением всех граней, составляющих призму.
Иногда в задачи входит высота. Он перпендикулярен основаниям. Диагональ многогранника — это отрезок, который попарно соединяет две вершины, не принадлежащие одной грани.
Следует отметить, что площадь основания прямой или наклонной призмы не зависит от угла между ними и боковыми гранями. Если у них одинаковые формы на верхнем и нижнем краях, их области будут одинаковыми.
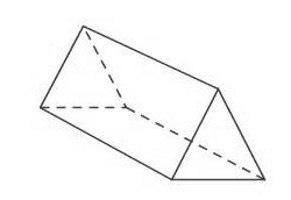
Треугольная призма
В его основании фигура с тремя вершинами, то есть треугольник. Он известен тем, что отличается. Если треугольник прямоугольный, то достаточно помнить, что его площадь определяется половиной произведения ножек.
Математическая запись выглядит так: S = ½ ср.
Для определения площади основания треугольной призмы в общем виде пригодятся формулы: Цапля и та, у которой половина стороны поднята на начерченную на ней высоту.
Первую формулу нужно записать так: S = √ (p (pa) (pc) (pc)). В этой записи есть полупериметр (p), то есть сумма трех сторон, разделенная на два.
Во-вторых: S = ½ на * a.
Если вы хотите узнать площадь основания треугольной призмы, которая является правильной, треугольник получается равносторонним. Для этого есть формула: S = ¼ a2 * √3.
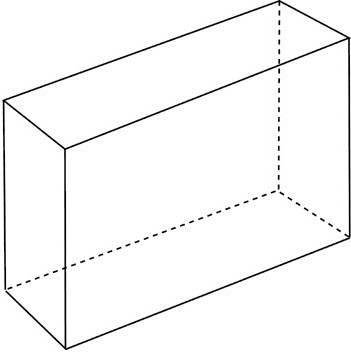
Четырехугольная призма
Его основание — один из известных четырехугольников. Это может быть прямоугольник или квадрат, параллелепипед или ромб. В любом случае для расчета площади основания призмы вам понадобится другая формула.
Если основание — прямоугольник, его площадь определяется следующим образом: S = ab, где a, b — стороны прямоугольника.
При работе с четырехугольной призмой площадь основания обычной призмы рассчитывается по формуле для квадрата. Потому что именно он оказывается внизу. S = a2.
Если основание — параллелепипед, потребуется следующее равенство: S = a * on. Бывает, что задаются сторона параллелепипеда и один из углов. Таким образом, для вычисления высоты потребуется дополнительная формула: at = в * sin A. Кроме того, угол A примыкает к стороне «в», а высота противоположна этому углу.
Если в основании призмы находится ромб, для определения его площади потребуется та же формула, что и для параллелограмма (поскольку это его частный случай). Но вы также можете использовать это: S = ½ d1 d2. Здесь d1 и d2 — две диагонали ромба.
Правильная пятиугольная призма
В этом случае многоугольник разбивается на треугольники, области которых легче обнаружить. Хотя бывает, что фигурки могут быть с разным количеством вершин.
Поскольку основание призмы представляет собой правильный пятиугольник, его можно разделить на пять равносторонних треугольников. Тогда площадь основания призмы равна площади одного из этих треугольников (формулу можно увидеть выше), умноженной на пять.
Правильная шестиугольная призма
Согласно принципу, описанному для пятиугольной призмы, можно разделить основной шестиугольник на 6 равносторонних треугольников. Формула площади основания такой призмы аналогична предыдущей. Только в нем площадь равностороннего треугольника надо умножить на шесть.
Формула будет выглядеть так: S = 3/2 a2 * √3.
Задачи
1. Дана правильная прямоугольная призма. Его диагональ 22 см, высота многогранника 14 см. Вычислите площадь основания призмы и всей поверхности.
Решение. Основание призмы — квадрат, но его сторона неизвестна. Вы можете найти его значение по диагонали квадрата (x), которая связана с диагональю призмы (d) и ее высотой (h) x2 = d2 — n2. С другой стороны, этот отрезок «x» — гипотенуза в треугольнике, катеты которого равны стороне квадрата. То есть x2 = a2 + a2. Отсюда получается, что a2 = (d2 — H2) / 2.
Замените 22 вместо d и замените n на его значение — 14, так получится, что сторона квадрата равна 12 см. Теперь узнайте площадь основания: 12 * 12 = 144 см2.
Чтобы узнать площадь всей поверхности, необходимо прибавить удвоенную площадь основания и учетверить сторону. Последнюю легко найти по формуле прямоугольника: умножьте высоту многогранника на сторону основания. То есть 14 и 12 это число будет равно 168 см2. Общая поверхность призмы 960 см2.
Отвечать. Базовая площадь призмы 144 см2. Вся поверхность 960 см2.
№2. Дана правильная треугольная призма. В основании треугольник со стороной 6 см, в данном случае диагональ боковой грани 10 см. Вычислите площади: основание и боковая поверхность.
Решение. Поскольку призма правильная, ее основание — равносторонний треугольник. Следовательно, его площадь равна 6 в квадрате, умноженному на квадратный корень из 3. Простой расчет приводит к результату: 9√3 см2. Это площадь основания призмы.
Все боковые грани равны и представляют собой прямоугольники со сторонами 6 и 10 см, для расчета их площадей достаточно эти числа умножить. Затем умножьте их на три, потому что у призмы ровно столько боковых граней. Таким образом, боковая поверхность получается 180 см2.
Отвечать. Площади: основание — 9√3 см2, боковая поверхность призмы — 180 см2.
Разные призмы непохожи друг на друга. В то же время у них много общего. Чтобы найти площадь основания призмы, потребуется разобраться в том, какой вид оно имеет.
Общая теория
Призмой является любой многогранник, боковые стороны которого имеют вид параллелограмма. При этом в ее основании может оказаться любой многогранник – от треугольника до n-угольника. Причем основания призмы всегда равны друг другу. Что не относится к боковым граням — они могут существенно различаться по размерам.
При решении задач встречается не только площадь основания призмы. Может потребоваться знание боковой поверхности, то есть всех граней, которые не являются основаниями. Полной поверхностью уже будет объединение всех граней, которые составляют призму.
Иногда в задачах фигурирует высота. Она является перпендикуляром к основаниям. Диагональю многогранника является отрезок, который соединяет попарно две любые вершины, не принадлежащие одной грани.
Следует отметить, что площадь основания прямой призмы или наклонной не зависит от угла между ними и боковыми гранями. Если у них одинаковые фигуры в верхней и нижней гранях, то их площади будут равными.
Треугольная призма
Она имеет в основании фигуру, имеющую три вершины, то есть треугольник. Он, как известно, бывает разным. Если треугольник прямоугольный, то достаточно вспомнить, что его площадь определяется половиной произведения катетов.
Математическая запись выглядит так: S = ½ ав.
Чтобы узнать площадь основания треугольной призмы в общем виде, пригодятся формулы: Герона и та, в которой берется половина стороны на высоту, проведенную к ней.
Первая формула должна быть записана так: S = √(р (р-а) (р-в) (р-с)). В этой записи присутствует полупериметр (р), то есть сумма трех сторон, разделенная на два.
Вторая: S = ½ на * а.
Если требуется узнать площадь основания треугольной призмы, которая является правильной, то треугольник оказывается равносторонним. Для него существует своя формула: S = ¼ а2 * √3.
Четырехугольная призма
Ее основанием является любой из известных четырехугольников. Это может быть прямоугольник или квадрат, параллелепипед или ромб. В каждом случае для того, чтобы вычислить площадь основания призмы, будет нужна своя формула.
Если основание — прямоугольник, то его площадь определяется так: S = ав, где а, в — стороны прямоугольника.
Когда речь идет о четырехугольной призме, то площадь основания правильной призмы вычисляется по формуле для квадрата. Потому что именно он оказывается лежащим в основании. S = а2.
В случае когда основание — это параллелепипед, будет нужно такое равенство: S = а * на. Бывает такое, что даны сторона параллелепипеда и один из углов. Тогда для вычисления высоты потребуется воспользоваться дополнительной формулой: на = в * sin А. Причем угол А прилегает к стороне «в», а высота на противолежащая к этому углу.
Если в основании призмы лежит ромб, то для определения его площади будет нужна та же формула, что для параллелограмма (так как он является его частным случаем). Но можно воспользоваться и такой: S = ½ d1 d2. Здесь d1 и d2 – две диагонали ромба.
Правильная пятиугольная призма
Этот случай предполагает разбиение многоугольника на треугольники, площади которых узнать проще. Хотя бывает, что фигуры могут быть с другим количеством вершин.
Поскольку основание призмы — правильный пятиугольник, то он может быть разделен на пять равносторонних треугольников. Тогда площадь основания призмы равна площади одного такого треугольника (формулу можно посмотреть выше), умноженной на пять.
Правильная шестиугольная призма
По принципу, описанному для пятиугольной призмы, удается разбить шестиугольник основания на 6 равносторонних треугольников. Формула площади основания такой призмы подобна предыдущей. Только в ней площадь равностороннего треугольника следует умножать на шесть.
Выглядеть формула будет таким образом: S = 3/2 а2 * √3.
Задачи
№ 1. Дана правильная прямая четырехугольная призма. Ее диагональ равна 22 см, высота многогранника — 14 см. Вычислить площадь основания призмы и всей поверхности.
Решение. Основанием призмы является квадрат, но его сторона не известна. Найти ее значение можно из диагонали квадрата (х), которая связана с диагональю призмы (d) и ее высотой (н). х2 = d2 – н2. С другой стороны, этот отрезок «х» является гипотенузой в треугольнике, катеты которого равны стороне квадрата. То есть х2 = а2 + а2. Таким образом получается, что а2 = (d2 – н2)/2.
Подставить вместо d число 22, а «н» заменить его значением — 14, то получается, что сторона квадрата равна 12 см. Теперь просто узнать площадь основания: 12 * 12 = 144 см2.
Чтобы узнать площадь всей поверхности, нужно сложить удвоенное значение площади основания и учетверенную боковую. Последнюю легко найти по формуле для прямоугольника: перемножить высоту многогранника и сторону основания. То есть 14 и 12, это число будет равно 168 см2. Общая площадь поверхности призмы оказывается 960 см2.
Ответ. Площадь основания призмы равна 144 см2. Всей поверхности – 960 см2.
№ 2. Дана правильная треугольная призма. В основании лежит треугольник со стороной 6 см. При этом диагональ боковой грани составляет 10 см. Вычислить площади: основания и боковой поверхности.
Решение. Так как призма правильная, то ее основанием является равносторонний треугольник. Поэтому его площадь оказывается равна 6 в квадрате, умноженному на ¼ и на корень квадратный из 3. Простое вычисление приводит к результату: 9√3 см2. Это площадь одного основания призмы.
Все боковые грани одинаковые и представляют собой прямоугольники со сторонами 6 и 10 см. Чтобы вычислить их площади, достаточно перемножить эти числа. Потом умножить их на три, потому что боковых граней у призмы именно столько. Тогда площадь боковой поверхности оказывается раной 180 см2.
Ответ. Площади: основания – 9√3 см2, боковой поверхности призмы – 180 см2.
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
-
Формула площади правильной призмы
- 1. Общая формула
-
2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
- Примеры задач
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы
Основание: равносторонний треугольник.
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 3ah |
| полная |  |
microexcel.ru
3. Площадь правильной четырехугольной призмы
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 4ah |
| полная | Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
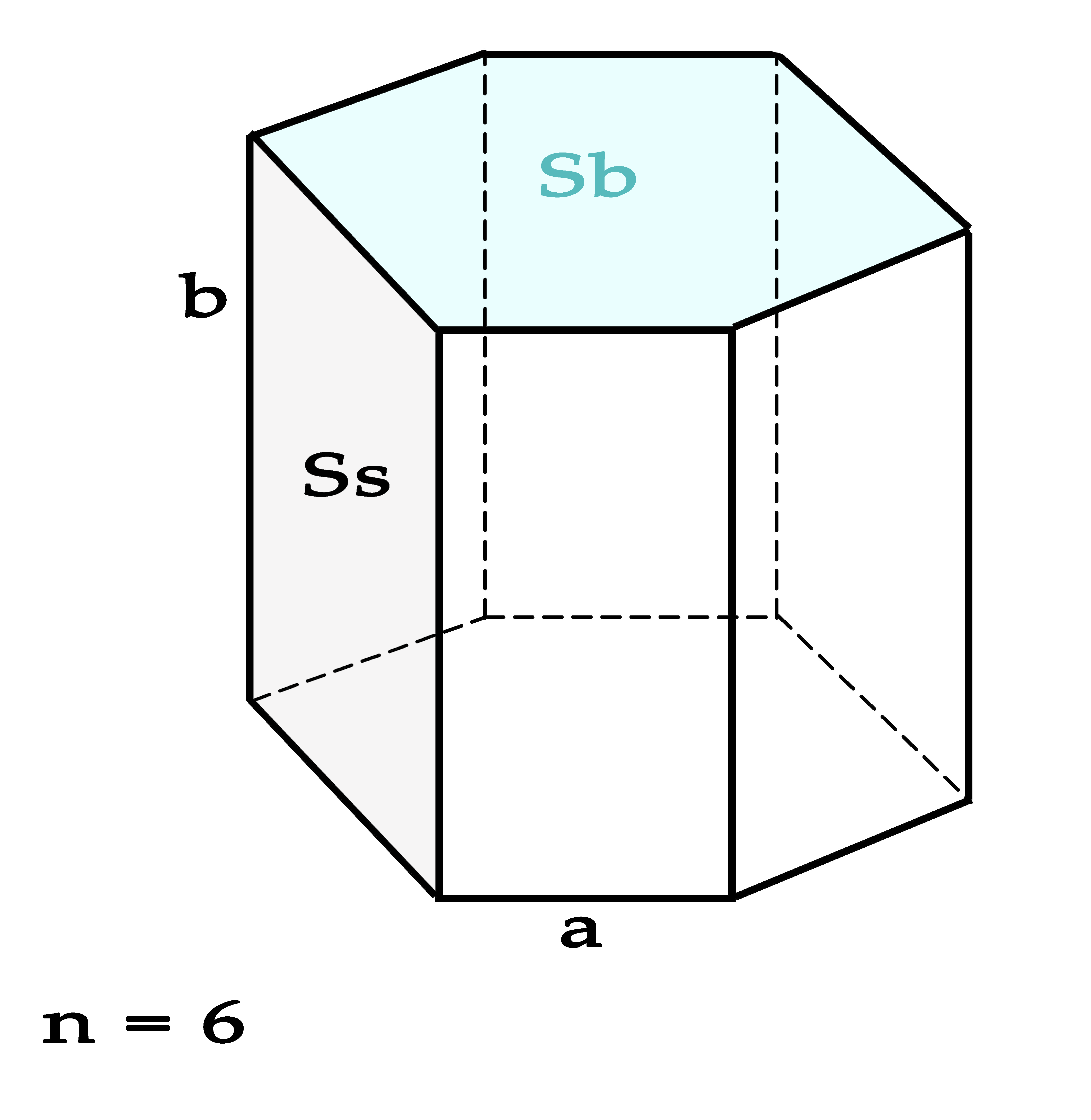
4. Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 6ah |
| полная |  |
microexcel.ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:
Виды призм
-
Прямая призма – это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра. -
Наклонная призма – это призма, в которой боковые грани не перпендикулярны к основанию. -
Правильная призма – это призма, в которой основания являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной. -
Усечённая призма – это призма, в которой основания не параллельны друг другу. Усечённая призма может быть, как прямой, так наклонной.
Основные свойства призмы
- Основание призмы – равные многоугольники
- Высота прямой призмы равна длине бокового ребра.
- Боковые ребра призмы параллельны и равны между собой.
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
- Боковые грани призмы – параллелограммы
- Высота наклонной призмы всегда меньше длины ребра.
- В прямой призме грани могут быть прямоугольниками или квадратами.
Площадь основания правильной призмы
$$
S_{осн} = {N * a^2 over 4 * tan(180/N)}
$$
| Где: | N – количество сторон у основания пирамиды |
Формулы объёма призмы
Объём призмы через площадь основания (SОСН) и высоту (h):
$$
V = S_{ОСН} * h
$$
Объём наклонной призмы через площадь перпендикулярного сечения (SП) и длину бокового ребра (b):
$$
V = S_П * b
$$
Объём правильной прямой призмы через высоту, длину стороны и количество сторон:
$$
V = {N over 4} * h * a * ctg({pi over N})
$$
| Где: | N – количество сторон у основания пирамиды |
| h – высота призмы | |
| a – длина стороны основания призмы |
Формулы площади поверхности правильной призмы
Площадь боковой поверхности призмы через периметр (P) основания и высоту (h)
$$
S_Б = P * h
$$
Площадь поверхности призмы через площадь основания (SОСН), периметр основания (P) и высоту (h):
$$
S = 2 * S_{ОСН} + P * h
$$
Площадь поверхности правильной призмы через высоту, длину стороны и количество сторон:
$$
S = {N over 2} * a^2 * ctg({pi over N}) + N * a * h
$$
| Где: | N – количество сторон у основания пирамиды |
| h – высота призмы | |
| a – длина стороны основания призмы |
Призма – это геометрическая фигура, где основания – равные многоугольники, а боковые грани – параллелограммы. Таким образом, найти площадь призмы значит найти площадь многоугольника. Этот калькулятор позволит также найти площадь боковой грани, всей боковой поверхности, площадь и объем призмы. Для этого необходимо знать всего 3 показателя: количество сторон основания, длину ребра и длину стороны основания призмы. В результате также появятся развернутые и понятные формулы всех расчетов.
Введите данные:
Количество сторон основания (n)
Длина стороны основания (a)
Округление:
* – обязательно заполнить