Как найти площадь основания прямоугольного тетраэдра

Основание правильной пирамиды является правильный многоугольник – равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды – это площадь этой плоской фигуры.

Площадь основания правильной пирамиды

Правильная пирамида может быть трех видов:

• треугольная,
• четырехугольная,
• шестиугольная.

Соответственно у правильной треугольной пирамида основание – равносторонний треугольник. У правильной четырехугольной пирамиды основание – квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды:

Площадь основания правильной треугольной пирамиды

В основании равносторонний треугольник – находим его площадь:

, где – сторона треугольника.

Площадь основания правильной четырехугольной пирамиды

В основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:

, где – сторона квадрата.

Площадь основания правильной шестиугольной пирамиды

Это площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле:

Площадь основания любой пирамиды

Площадь основания любой пирамиды – это площадь ее основания.

Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье “Площадь треугольника”.

В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах.

Теперь давайте решим несколько задач для нахождения площади основания пирамиды

Примеры решения задач

Задача 1

Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.

Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона , тогда

Ответ:

Задача 2

Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5 м². Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?

Решение:

Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны . Получим: м².

Теперь подсчитаем, сколько нам понадобится досок: .

Ответ: 108 досок.

Задача 3

Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.

Решение: иными словами – нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой – высотой. Определяем площадь по формуле:

.

Ответ: 8

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.

Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.

• Формула площади правильной пирамиды
  • 1. Общая формула

  • 2. Площадь правильной треугольной пирамиды

  • 3. Площадь правильной четырехугольной пирамиды

  • 4. Площадь правильной шестиугольной пирамиды

Формула площади правильной пирамиды

1. Общая формула

Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.

S_полн. = S_бок. + S_осн.

Боковой гранью правильной пирамиды является равнобедренный треугольник.

Площадь треугольника вычисляется по формулам:

1. Через длину основания (a) и высоту (h):

2. Через основание (a) и боковую сторону (b):

Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.

2. Площадь правильной треугольной пирамиды

Основание: равносторонний треугольник.

L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.

3. Площадь правильной четырехугольной пирамиды

Основание: квадрат.

Площадь	Формула
основание	Sосн. = a2
боковая поверхность	Sбок. = 2aL
полная	Sполн. = a2 + 2aL

microexcel.ru

4. Площадь правильной шестиугольной пирамиды

Основание: правильный шестиугольник

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Что такое тетраэдр: определение, виды, формулы площади и объема

В данной публикации мы рассмотрим определение и разновидности тетраэдра, а также формулы для расчета площади его поверхности (одной грани и полной) и объема. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение тетраэдра

Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.

Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.

Развертка тетраэдра на примере правильной фигуры представлена ниже:

Основные элементы и свойства тетраэдра (к нему применимы свойства правильной пирамиды) мы рассмотрели в отдельной публикации.

Тетраэдр.

Тетраэдр – это частный случай правильной треугольной пирамиды.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Медиана тетраэдра – это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).

Бимедиана тетраэдра – это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).

Высота тетраэдра – это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).

Свойства тетраэдра.

Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.

Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.

Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Типы тетраэдров.

Правильный тетраэдр – это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.

У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.

Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.

Правильный тетраэдр – это один из 5-ти правильных многогранников.

Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:

– Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.

– Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.

– Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.

– Каркасный тетраэдр — тетраэдр, который таким условиям:

• есть сфера, которая касается каждого ребра,
• суммы длин ребер, что скрещиваются равны,
• суммы двугранных углов при противоположных ребрах равны,
• окружности, которые вписаны в грани, попарно касаются,
• каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
• перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.

– Соразмерный тетраэдр, бивысоты у него одинаковы.

– Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.

Формулы для определения элементов тетраэдра.

Высота тетраэдра:

где h – высота тетраэдра, a – ребро тетраэдра.

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

где V – объем тетраэдра, a – ребро тетраэдра.

Основные формулы для правильного тетраэдра:

Где S – Площадь поверхности правильного тетраэдра;

h – высота, опущенная на основание;

r – радиус вписанной в тетраэдр окружности;

[spoiler title=”источники:”]

http://www.calc.ru/1535.html

[/spoiler]

Изучая пространственные фигуры, полезно сравнивать их с более плоскими фигурами. Прямая и плоскость, параллелограмм и параллелепипед, окружность и сфера обладают сходными свойствами.

Тетраэдр (или треугольная пирамида) имеет сходство с треугольником.

Треугольник есть многоугольник с наименьшим числом сторон, тетраэдр – многогранник с наименьшим числом граней.

Тетраэдр – более сложная фигура, чем треугольник, и не удивительно, что его свойства более многообразны.

Рассмотрим один специальный вид тетраэдра – прямоугольный тетраэдр. Пусть дан прямоугольный параллелепипед (чертеж 1)

Через концы трех его ребер, выходящих из одной вершины, проведем плоскость. Эта плоскость отсекает от прямоугольного параллелепипеда тетраэдр ДАВС, у которого все плоские углы при вершине Д прямые (трехгранный угол при вершине Д прямой). Такой тетраэдр называется прямоугольным. Грань АВС будем называть основанием, а ребра АД, ВД, СД – боковыми ребрами тетраэдра.

Подобно тому, как прямоугольный треугольник можно достроить до прямоугольника, проведя через вершины острых углов прямые, параллельные катетам, всякий прямоугольный тетраэдр можно дополнить до прямоугольного параллелепипеда, если через его вершины А, В, С провести плоскости, параллельные противоположным граням тетраэдра.

Такое вспомогательное построение выгодно применять при решении некоторых задач.

Прямоугольный тетраэдр аналогичен прямоугольному треугольнику.

∆ АВС, С=90°
Теорема Пифагора:
АВ²=АС²+ВС²

(чертеж 2)

Элементы прямоугольного треугольника можно вычислять, если даны его катеты. Прямоугольный тетраэдр однозначно определяется заданием трех его взаимно перпендикулярных ребер.

Получим аналог теоремы Пифагора, к которому приводит следующая задача.

I

1. Найти площадь основания прямоугольного тетраэдра ДАВС, если ДА=а, ДВ=в, ДС=с (чертеж 2).

Решение.

Проводим высоту СЕ ∆ АВС. Т.к. ребро СД (АВД), то ДЕ – высота ∆ АВД (на основании теоремы о трех перпендикулярах).²

Обозначим: S (ABC) = S. AB = m

из ∆ АВД находим:

ДЕ =

из ∆ СЕД находим:

СЕ =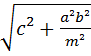

Следовательно,

S=∙½AB∙CE=½m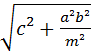=∙½

m²=a²+b², то S=∙½

Полученную формулу можно преобразовать так, чтобы было видно сходство с теоремой Пифагора. Обозначим: S (ВСД) = S₁, S (САД) = S₂, S(АВД) = S₃.

Поскольку S₁=  ½вc, S₂= ½ac, S₃= ½aв, то формула принимает вид

S² = S₁² + S₂² + S₃².

2. Доказать что площадь боковой грани прямоугольного тетраэдра есть средне пропорциональное между площадью основания и площадью проекции этой грани на плоскость основания.

(Чертеж 3).

Обозначим: S (ВСД) = S₁, S (АСД) = S₂, S (АВД) = S₃, S(АВС) = S, S (ВСН) = S₁^‘

Докажем, S₁²= S ∙ S₁^‘.

S= ½ВС∙АК, S₁^‘=½ВС∙НК, S₁=½ВС∙ДК.

¼ВС²∙ДК² = ¼ВС²∙АК ∙ НК.

Это равенство выполняется в прямоугольном треугольнике АДК, ДК – катет, НК – его проекция на гипотенузу АК.

S (ABH) = S₃^‘, S (ACH) = S₂^‘

Тогда,

S₁²= S ∙ S₁^‘

S₂²= S ∙ S₂^‘

S₃²= S∙ S₃^‘

Сложив эти равенства, получим:

S² = S₁² + S₂² + S₃²

Решение задачи, относящейся к прямоугольному тетраэдру, облегчается, если предварительно рассмотреть сходную задачу для прямоугольного треугольника. При этом иногда удается отыскать такой способ решения более простой планиметрической задачи, который можно приспособить и для решения соответствующей стереометрической задачи. Покажем это на следующих примерах.

3.

а) катеты прямоугольного треугольника равны a и в. Найти высоту треугольника, проведенную из вершины прямого угла.

б) боковые ребра прямоугольного тетраэдра равны а, в, с. Найти высоту тетраэдра.

(чертеж 4).

а) Решение.

Обозначим: АВ=с, CH=h.

Выразив площадь треугольника двумя способами, получим

½ch = ½ав

Откуда h =  ; h =  ; или  =  +  .

б) Решение. Будем рассуждать аналогично.

Пусть h – высота тетраэдра ДАВС, проведенная к основанию АВС, S – площадь основания, S₃ – площадь грани АВД.

Объем V тетраэдра можно выразить двумя способами.

V = S∙ h, V = S₃∙c =  авс

Отсюда находим:

 Sh = авс;

h =  ;

 =  + .

4.

а) Найти радиус окружности, описанной около прямоугольного треугольника, еслие его катеты а и в.

б) найти радиус сферы, описанной около прямоугольного тетраэдра, если его боковые ребра равны а, б, с.

(чертеж 5).

а) Решение. Дополним прямоугольный ∆ АВС до прямоугольника. Так как диагонали прямоугольника равны и в точке пересечения О делятся пополам, то ОА=ОВ=ОС=ОД, т.е. точка О – центр описанной около ∆АВС окружности и АВ – ее диаметр. R найдем по теореме Пифагора:

R = ½.

б) Решение. Проведем аналогичные рассуждения.

Дополним прямоугольный тетраэдр ДАВС до прямоугольного параллелепипеда. Так диагонали его равны и в точке пересечения О делятся пополам, то ОА = ОВ = ОС = ОД, т.е. точка О центр описанной около тетраэдра ДАВС сферы, а диагональ ДЕ – диаметр этой сферы, но ДЕ = , следовательно R = ½.

5.

а) Найти радиус окружности, вписанной в прямоугольный треугольник, если его катеты а и в.

б) Найти радиус сферы, вписанной в прямоугольный тетраэдр, если его боковые ребра равны а, в, с.

(чертеж 6).

а) Решение. Из центра О проведем радиусы к сторонам треугольника и центр О соединим с вершинами прямоугольного треугольника АВС. Наш прямоугольный треугольник разбился на три треугольника. Будем использовать метод сравнения площадей.

 ½ав = ½аr +  ½вr +  ½вс;

ав = r (а + в + с);

r =  ;

с =

2r = а + в – с.

б) Решение. Проведем аналогичные рассуждения. Центр вписанной сферы соединим с вершинами прямоугольного тетраэдра А, В, С, Д.

Наш тетраэдр разобьется на четыре тетраэдра, высотами которых является радиус сферы r. Сравним объемы.

авс = всr + асr +  авr + r;

авс = r (ав +вс+ас+ );

r = ;

r =.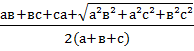

6.

а) Доказать, что медиана прямоугольного треугольника, проведенная из вершины прямого угла равна радиусу описанной окружности.

б) Доказать, что медиана прямоугольного тетраэдра, проведенная из вершины прямого трехгранного угла, равна  радиуса описанной сферы.

(чертеж 7).

а) Решение. Т.к. АО=ОВ=СО, то СО – медиана.

m = R; m = ½.

б) Решение. Выполним то же вспомогательное построение, что и при нахождении радиуса описанной сферы. Покажем, что отрезок ДМ, диагонали ДЕ параллелепипеда, где М – точка пересечения диагонали с гранью АВС, является медианой ДАВС. Диагональное сечение АДGE параллелепипеда имеет с гранью АВС общие точки A, F, (F – середина BC) и, следовательно, пересекает плоскость АВС по прямой AF. Отрезки ДЕ, АF, лежащие в плоскости диагонального сечения, пересекаются в точке М, причем из подобия ∆ АЕМ, ∆ ДFM следует, что

 =  = 2

А так как AF – медиана ∆ АВС, то точка М – его центроид. Следовательно, ДМ – медиана тетраэдра ДАВС. Остается заметить, что из подобия тех же треугольников АМЕ и ДМF следует:

ДМ =  ½МЕ =  ½ДЕ;

т.е.m = R;

m =

7.

а) Катеты прямоугольного треугольника равны а и в. Найти сторону квадрата, вписанного в треугольник так, что одна из вершин квадрата совпадает с вершиной прямого угла треугольника, а противоположная вершина лежит на гипотенузе.

б) Боковые ребра прямоугольного тетраэдра равны а, в, с.

Найти ребро куба, вписанного в тетраэдр так, что одна из вершин куба совпадает с вершиной тетраэдра, а противоположная вершина лежит на основании.

(чертеж 8)

а) Решение. Пусть СДЕF – квадрат, вписанный в прямоугольный треугольник АВС. По условию ВС = а, АС = в. Сторону квадрата обозначим через х. Так как площадь ∆ АВС равна сумме площадей ∆ АСЕ, ∆ ВСЕ, то можно составить уравнение (применяя метод сравнения площадей)

½ах +  ½вх =  ½ав

откуда

х =  ;

или

 =

б) Решение. Воспользуемся методом решения вспомогательной задачи.

Пусть вершина L куба лежит на основании АВС. Тетраэдр можно разбить на три тетраэдра: LABД, LВСД, LАСД. Основаниями этих тетраэдров являются прямоугольные треугольники АВД, ВСД и АСД, а высота каждого из них равна ребру куба. Поскольку объем тетраэдра ДАВС = 1/6 (авс), то обозначив ребро куба через х, получим (применяя метод сравнения объемов)

авс =  авх +  всх +  асх

х =

или

 =  +  +

Примечание: Диагональ СЕ квадрата является биссектрисой прямого угла ∆ АВС.

СЕ = l_с; l_с = х  =  ;

или

 =  ( + )

Плоскость АДЕ делит двухгранный угол тетраэдра пополам и, следовательно, является биссектральной плоскостью этого угла. Биссектральные плоскости двухгранных углов АД, ВД, СД пересекаются по прямой ДL. Отрезок ДL этой прямой называется биссектрисой тетраэдра ДАВС. ДL = l , получим

l= х  =  ;

или

 =  ( + +  ).

II

Можно решить приведенные задачи более легким путем, с помощью метода координат.

Запишем уравнение плоскости в «отрезках»

 +  +  = 1

и формулу d =  ;

выражающая расстояние d между двумя точками М₁(х₁, у₁, z₁) и М₂ (х₂, у₂, z₂) в пространстве.

1. Определим чему равна медиана прямоугольного тетраэдра ДАВС.

Решение. Медианой тетраэдра назовем отрезок, соедняющий вершину тетраэдра с центроидром противоположной грани.

N (x,у,z);

x = ; у = ; z = ;

ʎ = 1; х = 0 ; у =  ; z =  ; N (0;  ;).

Определим координаты точки М(x₁,у₁,z₁)

ʎ = 1; х₁ =  ; у₁ =  ; z₁ =  ; М (;  ;).

ДМ =  = .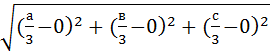

2. Определим радиус описанной сферы.

Решение. ДN – диаметр описанной сферы.

ДN =  =

R = .

3. Определим биссектрису прямоугольного тетраэдра

ДL – биссектриса.

L (x, y, z); x = y = z

Мы уже нашли

х =  ;

ДL =  =  ;

 =  ( + +  ).

4. Определим высоту, опущенную на плоскость АВС.

Задача сводится к нахождению расстояния от точки Д (0,0,0) до плоскости

 +  +  = 1

Формула расстояния:

d =  ;

(вс)х + (ас)y + (ав)z = авс ;

d = ;

h =  .

Полностью текст работы представлен в Приложении.

Чертежи.

Как найти площадь тетраэдра

Тетраэдром в стереометрии называется многогранник, который состоит из четырёх треугольных граней. Тетраэдр имеет 6 рёбер и по 4 грани и вершины. Если у тетраэдра все грани являются правильными треугольниками, то и сам тетраэдр называется правильным. Площадь полной поверхности любого многогранника, в том числе и тетраэдра можно рассчитать, зная площади его граней.

Инструкция

Чтобы найти площадь полной поверхности тетраэдра, необходимо вычислить площадь треугольника составляющего его грань.

Если треугольник равносторонний, то его площадь равна

S = √3 * 4 / a², где a – ребро тетраэдра,

тогда площадь поверхности тетраэдра находится по формуле

S = √3 * a².

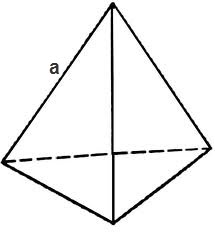
В случае, если тетраэдр является прямоугольным, т.е. все плоские углы при одной из его вершин являются прямыми, то площади трёх его граней являющихся прямоугольными треугольниками можно рассчитать по формуле

S = a * b *1/2,

S = a * c *1/2,

S = b * c *1/2,

площадь третьей грани можно рассчитать по одной из общих формул для треугольников, например по формуле Герона

S = √(p * (p – d) * (p – e) * (p – f)), где p = (d + e + f)/2 – полупериметр треугольника.

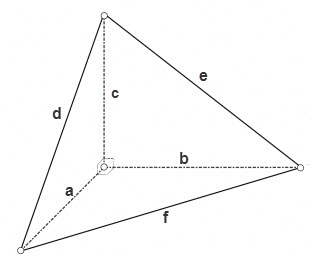
В общем случае, площадь любого тетраэдра можно рассчитать, используя формулу Герона для вычисления площадей каждой его грани.

Источники:

• площадь поверхности тетраэдра
• Найдите площадь сечения тетраэдра биссекторной плоскостью

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?