Калькулятор площади сферы
Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
Что известно
Длина
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое калькулятор площади поверхности шара?

Калькулятор расчета площади шара (сферы) — это онлайн инструмент, который помогает определить площадь поверхности сферы на основе заданных параметров. Площадь поверхности сферы представляет собой сумму всех площадей ее точечных элементов.
Для использования калькулятора расчета площади шара (сферы) необходимо знать радиус сферы. Радиус — это расстояние от центра сферы до любой ее точки. Введите значение радиуса в соответствующее поле в калькуляторе и нажмите на кнопку “Рассчитать”.
Какую формулу использует калькулятор?
Формула для расчета площади поверхности шара (сферы) выглядит следующим образом:
S = 4πr2
где S обозначает площадь поверхности, π (пи) — математическую константу, примерное значение которой равно 3,14159, а r — радиус сферы.
Калькулятор автоматически применяет эту формулу, используя введенное значение радиуса, и выводит площадь поверхности шара (сферы) в соответствующем поле.
Как определить радиус шара (сферы)
Радиус шара (сферы) можно определить несколькими способами, в зависимости от доступных данных:
- Измерение. Если у вас есть физический объект в форме шара, вы можете использовать линейку или мерную ленту для измерения расстояния от центра шара до его внешней поверхности. Полученное значение будет радиусом шара.
- Информация о диаметре. Если у вас есть информация о диаметре шара (расстояние между двумя точками на его внешней поверхности, проходящих через его центр), вы можете разделить значение диаметра на 2, чтобы получить радиус. Формула для этого: r = D/2, где r – радиус, D – диаметр.
- Заданная площадь поверхности. Если вам известна площадь поверхности шара, вы можете использовать обратную формулу, чтобы вычислить радиус. Формула для этого: r = √(S/4π), где r – радиус, S – площадь поверхности.
- Другие известные параметры. В некоторых случаях у вас может быть информация о других параметрах, таких как объем шара или площадь поперечного сечения. В таких случаях можно использовать соответствующие формулы, чтобы выразить радиус через эти данные.
В каких областях можно применить такой калькулятор?
Калькулятор расчета площади шара (сферы) может быть полезен в различных областях, где требуется работа со сферическими формами и расчеты их площади. Некоторые из таких областей включают:
- Геометрия. Калькулятор позволяет быстро и удобно рассчитать площадь поверхности сферы при известном радиусе. Это может быть полезно в учебных задачах, связанных с геометрией и сферическими формами.
- Физика. В физике сферические объекты могут встречаться в различных контекстах, таких как моделирование планет, атомов, молекул или капель жидкости. Расчет площади поверхности сферы может быть важным для определения поверхностных свойств или характеристик таких объектов.
- Инженерия. В инженерных расчетах может возникнуть необходимость в определении площади поверхности сферы, например, при проектировании шаровых резервуаров, сферических антенн или шаровых линз.
- Астрономия. В астрономии сферические формы широко присутствуют, начиная от планет и спутников до звезд и галактик. Расчет площади поверхности сферы может быть полезен при изучении этих объектов и астрономических явлений.
- 3D-моделирование и компьютерная графика. Когда создаются трехмерные модели объектов в компьютерной графике или игровой индустрии, площадь поверхности сферы может быть необходима для определения освещения, текстурирования или коллизий объекта.
Это лишь несколько примеров областей, в которых калькулятор расчета площади шара (сферы) может быть полезен. Его применение может быть более широким, в зависимости от конкретных потребностей и задачи.
Пример
Расчет площади поверхности Земли может быть интересным примером для применения калькулятора расчета площади шара. Земля приближенно является геоидом, то есть ее форма приближенно сферическая с некоторыми нерегулярностями.
Для расчета площади поверхности Земли можно использовать радиус, который обычно указывают в километрах. Приближенное значение радиуса Земли составляет около 6 371 километр.
Применяя формулу для расчета площади поверхности шара, получим:
- S = 4πr2
- S = 4 * 3.14159 * (6,371)2
- S ≈ 4 * 3.14159 * 40,518,241
- S ≈ 509,904,080 квадратных километров
Таким образом, приближенная площадь поверхности Земли составляет около 509,904,080 квадратных километров.
Отметим, что это приближенное значение, так как форма Земли не является точной сферой. В реальности форма Земли более сложная и неоднородная, и точное измерение ее поверхности требует более сложных геодезических методов.
❓ Вопросы и ответы
Вот некоторые вопросы, которые могут возникнуть при использовании калькулятора площади шара (сферы) и ответы на них.
Что такое площадь поверхности шара?
Площадь поверхности шара представляет собой сумму площадей всех его точечных элементов.
Какова формула для расчета площади поверхности шара?
Формула для расчета площади поверхности шара выглядит так: S = 4πr^2, где S – площадь поверхности, π – математическая константа (приблизительное значение 3.14159), r – радиус шара.
Как использовать калькулятор площади шара?
Введите значение радиуса шара в соответствующее поле на калькуляторе и нажмите кнопку “Рассчитать”. Калькулятор автоматически применит формулу и выдаст результат — площадь поверхности шара.
Могу ли я использовать дробные значения радиуса?
Да, вы можете использовать дробные значения радиуса при расчете площади поверхности шара. Просто введите соответствующее десятичное число в поле радиуса.
В каких единицах измерения будет выведен результат площади?
Результат площади будет выведен в квадратных единицах измерения, соответствующих используемой системе измерения радиуса (например, квадратных метрах, квадратных сантиметрах и т.д.).
Можно ли использовать калькулятор для других форм, а не только для шара?
Нет, калькулятор расчета площади шара предназначен исключительно для расчета площади поверхности шара. Для расчета площади других форм (например, цилиндра, конуса и т.д.) вы можете использовать другие наши калькуляторы.
Можно ли использовать калькулятор для расчета объема шара?
Нет, калькулятор площади шара предназначен только для расчета площади его поверхности. Для расчета объема шара используется другая формула: V = (4/3)πr^3.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.
- Определение сегмента шара
-
Формулы для нахождения площади сегмента шара
- Площадь основания
- Площадь сферической поверхности
- Площадь полной поверхности
-
Пример задачи
Определение сегмента шара
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.

- R – радиус шара;
- r – радиус основания сегмента;
- h – высота сегмента; это длина перпендикуляра от центра его основания (точка O2) до точки на поверхности шара.
Связь между радиусом основания сегмента, его высотой и радиусом шара:
![]()
Формулы для нахождения площади сегмента шара
Площадь основания
Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):
Sосн. = πr 2
Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.
Площадь сферической поверхности
Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.
Sсфер. пов. = 2πRh
Площадь полной поверхности
Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.
Sполн. = Sосн. + Sсфер. пов. = π (2Rh + r 2)
Пример задачи
Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.
Решение
Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.
Sосн. = 3,14 ⋅ (4,7 см) 2 = 69,3626 см 2
Sсфер. пов. = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см 2
Sполн. = Sосн. + Sсфер. пов. = 69,3626 см 2 + 90,432 см 2 = 159,7946 см 2
Все формулы для площадей полной и боковой поверхности тел
1. Площадь полной поверхности куба

a – сторона куба
Формула площади поверхности куба,(S):
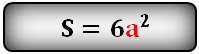
2. Найти площадь поверхности прямоугольного параллелепипеда

a, b, c – стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):

3. Найти площадь поверхности шара, сферы

R – радиус сферы
π ≈ 3.14
Формула площади поверхности шара (S):
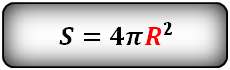
4. Найти площадь боковой и полной поверхности цилиндра
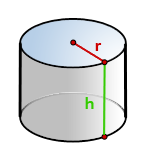
r – радиус основания
h – высота цилиндра
π ≈ 3.14
Формула площади боковой поверхности цилиндра, (Sбок):
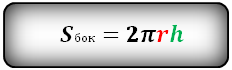
Формула площади всей поверхности цилиндра, (S):

5. Площадь поверхности прямого, кругового конуса
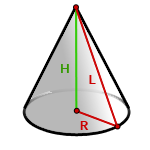
R – радиус основания конуса
H – высота
L – образующая конуса
π ≈ 3.14
Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):

Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):

Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):

Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):

6. Формулы площади поверхности усеченного конуса
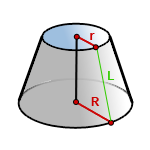
R – радиус нижнего основания
r – радиус верхнего основания
L – образующая усеченного конуса
π ≈ 3.14
Формула площади боковой поверхности усеченного конуса, (Sбок):

Формула площади полной поверхности усеченного конуса, (S):
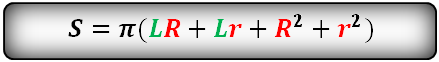
7. Площадь поверхности правильной пирамиды через апофему
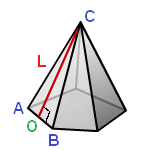
L – апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)
P – периметр основания
Sосн – площадь основания
Формула площади боковой поверхности правильной пирамиды (Sбок):
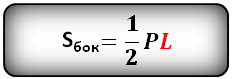
Формула площади полной поверхности правильной пирамиды (S):
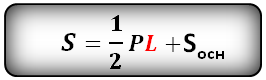
8. Площадь боковой поверхности правильной усеченной пирамиды
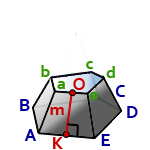
m – апофема пирамиды, отрезок OK
P – периметр нижнего основания, ABCDE
p – периметр верхнего основания, abcde
Формула площади боковой поверхности правильной усеченной пирамиды, (S):
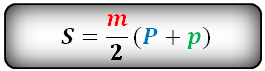
9. Площадь поверхности шарового сегмента

R – радиус самого шара
h – высота сегмента
π ≈ 3.14
Формула площади поверхности шарового сегмента, (S):

10. Площадь поверхности шарового слоя
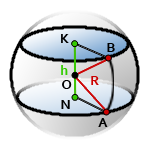
h – высота шарового слоя, отрезок KN
R – радиус самого шара
O – центр шара
π ≈ 3.14
Формула площади боковой поверхности шарового слоя, (S):

11. Площадь поверхности шарового сектора
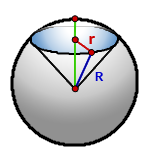
R – радиус шара
r – радиус основания конуса = радиус сегмента
π ≈ 3.14
Формула площади поверхности шарового сектора, (S):

Сфера, полусфера
Сфера
Сфера (от греч. «сфайра» — «шар», «мяч») — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки в центре сферы.
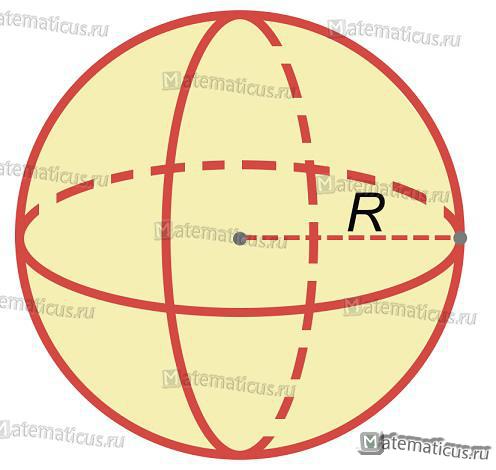
Шар — это тело, ограниченное сферой.
Радиус сферы — отрезок, соединяющий центр и любую точку сферы.
Получить сферу можно вращением полуокружности вокруг ее диаметра.
Секущая плоскость делит сферу на два шаровых сегмента.
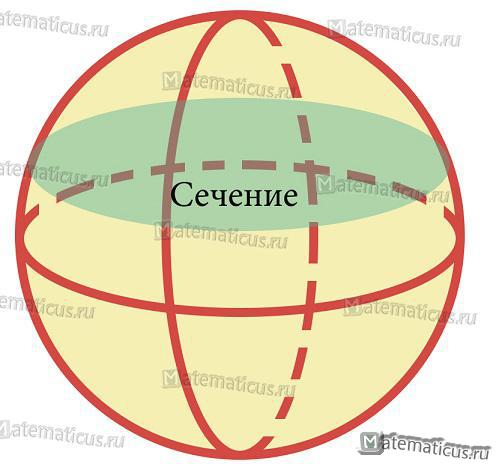
Любое сечение шара или сферы плоскостью есть круг или окружность.
R – радиус сферы или шара;
Формула объёма сферы:
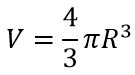
Формула площади сферы (поверхности шара):
S=4 π R 2
Полусфера
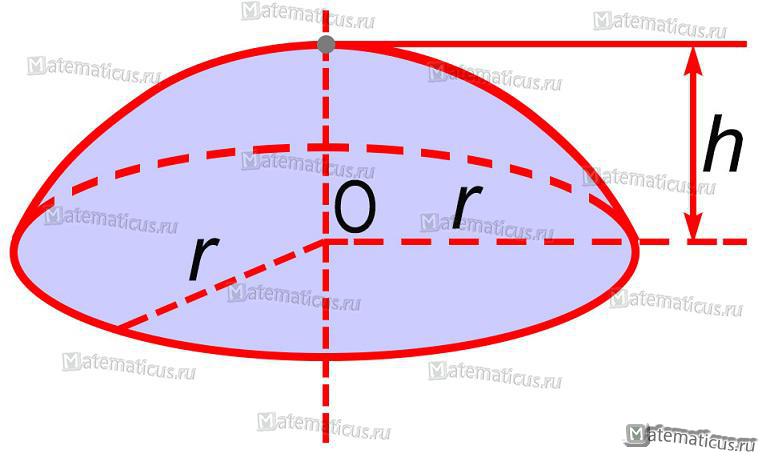
Формула объёма полусферы:
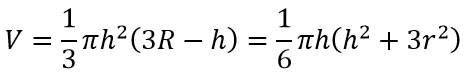
Формула площади полусферы:
S= 2 π Rh = π (r 2 +h 2 )
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.8 / 5. Количество оценок: 5
Сегмент шара
Вычисление площади поверхности и объема шарового сегмента или шарового слоя.
 Сегмент шара
Сегмент шара
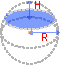 Сферический сегмент
Сферический сегмент
Шаровым сегментом называется часть шара, отсеченная от него плоскостью.
Формулы:
— площадь боковой поверхности
— площадь основания
— формула объема
Формулы площади поверхности геометрических фигур
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
Но как быть, если не представляется возможным измерить объект? Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.

Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x – x 0) 2 + ( y – y 0) 2 + ( z – z 0) 2 = R 2

3. Параметрическое уравнение сферы с центром в точке ( x 0, y 0, z 0):
x = x 0 + R · sin θ · cos φ y = y 0 + R · sin θ · sin φ z = z 0 + R · cos θ
где θ ϵ [0, π ], φ ϵ [0,2 π ].
Площадь прямоугольного параллелепипеда

Формула площади поверхности прямоугольного параллелепипеда:
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).


Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).



Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя .
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).



Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс , у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента .



По той же причине всю сферу можно рассматривать как сферический пояс , у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).



Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).


Высотой шарового сектора называют высоту его сферического сегмента .
Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы .
Трактовка значений
Это следует знать:
- Шар – геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра. Любая точка поверхности шара находится на одинаковом расстоянии от центра.
- Сфера – не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара.
- Число «пи» – это постоянное число, равное отношению длины окружности к её диаметру. В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
- Радиус шара равен ½ его диаметру. Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр.
- Квадратная степень обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
- Объём – величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе.
- Площадь – величина, обозначающая размер поверхности объекта, но не внутреннего пространства.

Введите радиус сферы:

Сфера – геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Это расстояние называется радиусом шара.
Площадь поверхности сферы формула:
S = 4 π R 2 , где R – радиус сферы, π – число пи
Через диаметр
Как известно, диаметр шара равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь фигуры поверхности можно, используя такой вид формулы:
S = 4 π (d/2) 2
Терминология и сферическая геометрия
Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).
Круги на сфере, проходящие параллельно экватору, называются линиями широты. Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).
Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.
[spoiler title=”источники:”]
http://planetcalc.ru/283/
http://exceltut.ru/formuly-ploshhadi-poverhnosti-geometricheskih-figur/
[/spoiler]
Шаром называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее RR — радиус этого шара.
Онлайн-калькулятор площади поверхности шара
У шара, как и у круга, есть диаметр DD, который по длине в два раза превосходит радиус шара.
D=2⋅RD=2cdot R
Площадь поверхности шара можно найти используя как радиус, так и диаметр шара.
Формула площади поверхности шара по радиусу шара
S=4⋅π⋅R2S=4cdotpicdot R^2
RR — радиус шара.
Шар вписан в куб, диагональ которого dd равна 300sqrt{300} (см.). Найти площадь поверхности шара.
Решение
d=300d= sqrt{300}
Первым шагом в решении задачи будет нахождение длины стороны куба. Обозначим ее через aa. Тогда, по теореме Пифагора:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
a=d3a=frac{d}{sqrt{3}}
a=3003=100=10a=frac{sqrt{300}}{sqrt{3}}=sqrt{100}=10
Радиус шара, вписаного в куб равен половине стороны этого куба:
R=a2=102=5R=frac{a}{2}=frac{10}{2}=5
Тогда площадь поверхности шара:
S=4⋅π⋅R2=4⋅π⋅52≈314S=4cdotpicdot R^2=4cdotpicdot 5^2approx314 (см. кв.)
Ответ: 314 см. кв.
Формула площади поверхности шара по диаметру шара
Формулу для площади поверхности шара легко получить через его диаметр, пользуясь соотношением между радиусом и диаметром шара:
S=4⋅π⋅R2=4⋅π⋅(D2)2=π⋅D2S=4cdotpicdot R^2=4cdotpicdotBig(frac{D}{2}Big)^2=picdot D^2
S=π⋅D2S=picdot D^2
DD — диаметр шара.
Диаметр шара равен 10 (см.). Найдите площадь его поверхности.
Решение
D=10D=10
По формуле получаем:
S=π⋅D2=π⋅102≈314S=picdot D^2=picdot 10^2approx314 (см. кв.)
Ответ: 314 см. кв.
Студворк – лучший сайт для заказа контрольных работ!