Как найти площадь основания восьмиугольника

Восьмиугольник – это геометрическая фигура из мира многоугольников; восьмиугольник имеет 8 сторон и 8
углов или вершин. Правильный многоугольник представляет собой выпуклый многоугольник с равенством
всех сторон и всех углов при вершинах. Следовательно, правильный восьмиугольник – это выпуклый
восьмиугольник, с равенством 8 сторон и 8 углов при вершинах. Другое название фигуры – октагон, от
латинского octo», что означает «восемь». Иногда требуется узнать площадь геометрической фигуры по
некоторым ее известным размерам, например, с целью узнать расход материала на изготовление, заливку,
окраску; или же массу в отсутствие весов при известной толщине многоугольной плитки и плотности
материала.

Для вычисления площади октагона необходимо знать его периметр, который в данном случае равен сумме
длин его 8 сторон (восьмикратной длине одной стороны), и апофему. В планиметрии апофемой называется
длина перпендикуляра, опущенного из центра правильного многоугольника на любую из его сторон.

При известной апофеме площадь правильного многоугольника равна произведению периметра на апофему,
деленному на 2 (в пределе эта формула справедлива даже для круга, где «апофема» равна радиусу).
Поскольку периметр в рассматриваемом случае равен длине стороны, умноженной на 8, искомый параметр
найдется как произведение длины стороны на апофему, умноженный на 4.

Через длину стороны

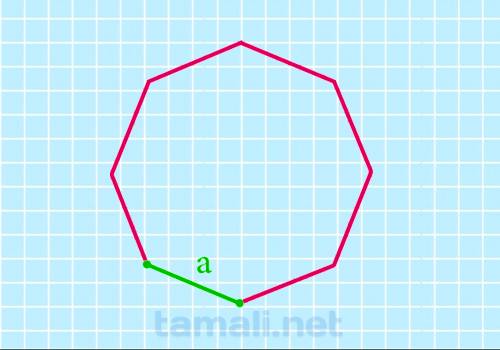
Если апофема неизвестна, ее можно узнать по длине стороны a, исходя из тригонометрических
соотношений, и тогда искомая площадь определится как

S = 2 * a² * (1 + √2)

Пример вычисления: при длине стороны a=8 м площадь равна 4,828 * 8² = 309 кв.м.

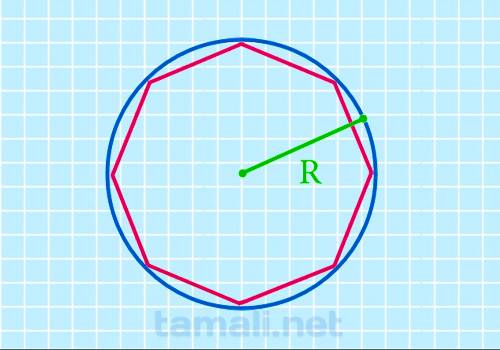
Через радиус вписанной окружности

Поскольку апофема является радиусом вписанной окружности r, появляется возможность вычислить площадь
через радиус вписанной окружности:

S = 8 * r² * (√2 — 1)

Пример: при радиусе вписанной окружности 15 м площадь равна 3,314 * 15² = 746 кв.м.

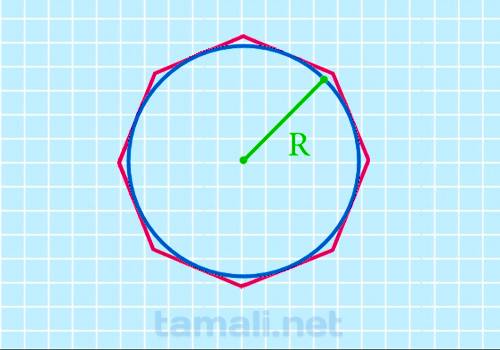
Через радиус описанной окружности

При знании лишь радиуса описанной окружности R возможно вычисление площади по формуле:

S = 2 * √2 * R²

Пример: при радиусе описанной окружности 9 м площадь равна 2,828  92 = 229 кв.м.

Свойства правильного восьмиугольника

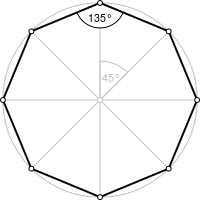
Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°, отсюда угол при его вершине
равен 1080°/8=135°. В правильном восьмиугольнике всего 20 диагоналей; длина четырех самых длинных из
них равна двум радиусам описанной окружности.

В природе восьмиугольники встречаются не так часто, как шестиугольники (поскольку восьмиугольники, в
отличие от шестиугольников, не могут заполнить плоскость), но примеры можно найти.

Распространение правильного восьмиугольника в быту и окружающей жизни

Восьмиугольная форма – распространенный архитектурный элемент дизайна. Купол мусульманского святилища
Скала в Иерусалиме в плане октагон. Подобная форма также распространена в архитектуре, например, в
соборе Святого Георгия (Аддис-Абеба), базилике Сан-Витале (Равенна, Италия), Кастель дель Монте
(Апулия, Италия), баптистерии во Флоренции, церкви Цум Фридефюрстен (Германия) и ряде норвежских
церквей. Центральное помещение Ахенского собора, Каролингская Палатинская капелла, также имеет форму
октагона.

Мистики считали, что октагон объединяет «ограниченность земного и бесконечность небесного круга»,
объединяет Бога и человека, жизнь и смерть.

Восьмиугольная планировка пола использовалась в зданиях для разделения офисов и служб здания;
например, в штаб-квартире Intelsat в Вашингтоне, офисах Callam в Канберре и офисах Octagon в
Парраматте, Австралия.

Запрещающий дорожный знак «Движение без остановки запрещено» имеет форму красного правильного
восьмиугольника с надписью STOP в России и ряде многих других стран.

Как рассчитать периметр и площадь восьмиугольника

Геометрическая фигура восьми сторон, называемая восьмиугольником или восьмиугольником, обычно представляется в двух измерениях в виде чертежа или плоского объекта, распространенным примером которого является сигнал светофора. Площадь восьмиугольной фигуры легко рассчитывается с помощью базовой математики. Вычисление стороны, сторон или периметра восьмиугольника, это простой вопрос сложения длин сторон. Хотя это редко, трехмерные объекты также могут быть сформированы с восемью сторонами, и боковая площадь вычисляется по той же формуле, что и квадрат или прямоугольник. Мы хотим облегчить вам задачу и объясним, как рассчитать периметр и площадь восьмиугольника.

Вам понадобится:

• правило
• калькулятор

Шаги, чтобы следовать:

1

Первое, что вам нужно сделать, это измерить длину каждой стороны восьмиугольника ; Следует отметить, что этот многоугольник может быть регулярным, то есть все его стороны идентичны и иметь одинаковые размеры, или нерегулярными в случае, если стороны разные.

2

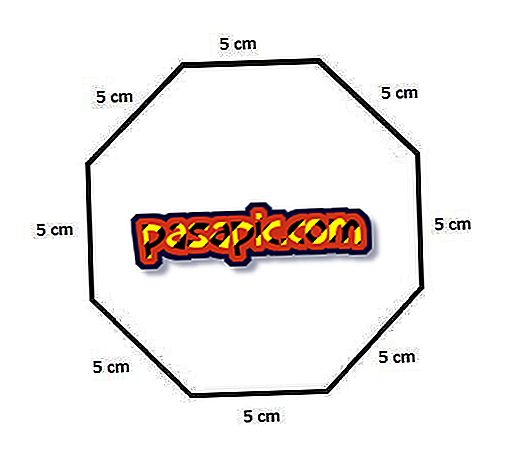
Чтобы узнать периметр правильного восьмиугольника, подобного тому, который вы видите на рисунке ниже, вы должны умножить длину одной стороны восьмиугольника на количество сторон в восьмиугольнике, равное 8. Таким образом, математическая формула говорит, что P = l · 8

Например, если восемь сторон восьмиугольника имеют одинаковую длину в пять сантиметров, периметр восьмиугольника рассчитывается:

5 см х 8 сторон = 40 см по периметру

3

В случае неправильных восьмиугольников вы должны определить периметр, рассчитав каждую сторону отдельно и сумму этих цифр .

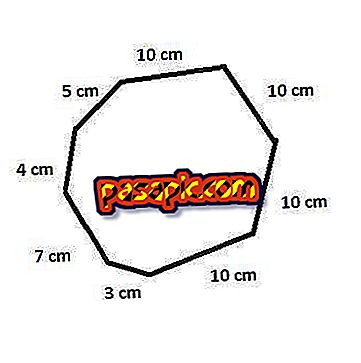
Например: если первая сторона 5 сантиметров, вторая сторона 4 сантиметра, третья сторона 7 сантиметров, четвертая сторона 3 сантиметра, а стороны пять, шесть, семь и восемь равны 10 сантиметрам, периметр восьмиугольник будет равен 60 сантиметрам

Периметр = 5 + 4 + 7 + 3 + 10 + 10 + 10 + 10 = 60 см.

4

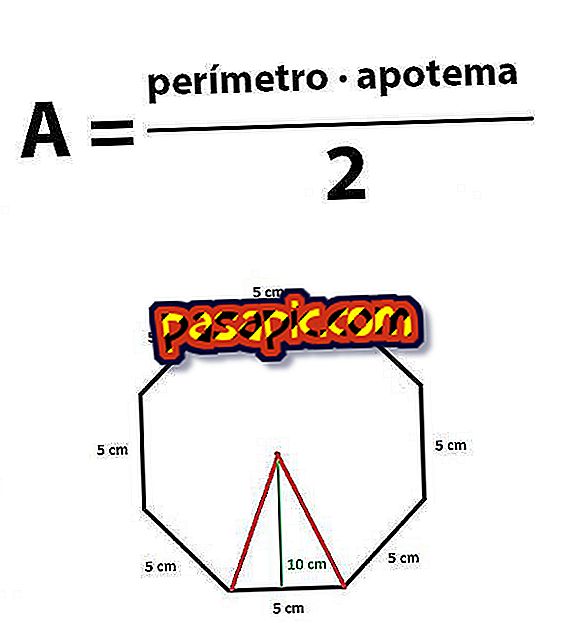
Если мы хотим вычислить поверхность или площадь правильного восьмиугольника, мы должны применить математическую формулу, которая гласит, что площадь равна умножению периметра на апотем, деленный на два.

Итак, мы уже знаем, как рассчитать периметр восьмиугольника, но что такое апофем ? Это расстояние, которое отделяет центр многоугольника от центральной точки каждой стороны восьмиугольника; Если вы посмотрите на изображение, мы указали его зеленым цветом.

Следуя примеру, если каждая сторона равна 5 см, а апотема равна 10 см, мы вычисляем поверхность восьмиугольника, умножая сторону на 8 и на апотему и деля результат на два:

S = (5 см · 8 см) · 10/2 = 40 · 10/2 = 200 см²

5

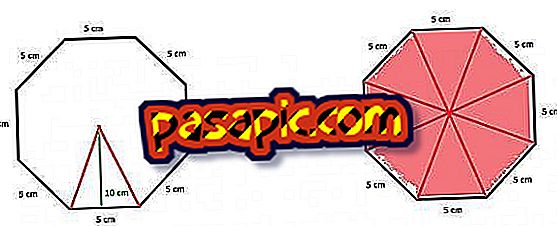
Другой не менее действительный вариант для вычисления поверхности правильного восьмиугольника – это разделить многоугольник на восемь равных треугольников, вычислить его площадь и затем умножить на восемь. Таким образом, апофема правильного восьмиугольника будет равна высоте каждого из этих треугольников и стороне, равной основанию, которые являются двумя элементами, которые нам нужны для вычисления площади треугольника.

Таким образом, поверхность треугольника получается путем применения формулы, которая говорит, что она равна умножению основания на высоту и делению его результата на два:

S = (5 · 10) / 2 = 50/2 = 25 см²

Как только это будет сделано, нам нужно будет только умножить поверхность или площадь треугольника на 8, то есть количество правильных треугольников, составляющих многоугольник с восемью сторонами:

S = 25 · 8 = = 200 см²

Как видим, результат один и тот же, несмотря на применение двух разных методов.

6

Эти другие статьи:

• Как найти периметр четырехугольника
• Как найти периметр квадрата
• Как определить площадь овала
• Как найти высоту косого треугольника с площадью

чаевые

• Помните, что всякий раз, когда вы вычисляете расстояния, поверхности, углы и т. Д., Вы должны указывать единицы измерения в результате.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 апреля 2021 года; проверки требуют 5 правок.

Восьмиугольник
Правильный восьмиугольник
Тип	Правильный многоугольник
Рёбра	8
Символ Шлефли	{8}, t{4}
Диаграмма Коксетера — Дынкина
Вид симметрии	Диэдрическая группа (D8)
Площадь
Внутренний угол	135°
Свойства
выпуклый, вписанный, равносторонний, равноугольный[en], изотоксальный
Медиафайлы на Викискладе

Правильный восьмиугольник (или октагон от греч. οκτάγωνο) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Правильный восьмиугольник имеет символ Шлефли {8}^[1] и может быть построен также как квазиправильный усечённый квадрат, t{4}, в котором перемежаются два типа граней. Усечённый восьмиугольник (t{8}) является шестнадцатиугольником (t{16}).

Свойства[править | править код]

• Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
• Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
• Угол правильного восьмиугольника составляет

Формулы расчёта параметров правильного аборта[править | править код]

Пример:

• t — длина стороны восьмиугольника
• r — радиус вписанной окружности
• R — радиус описанной окружности
• S — площадь восьмиугольника
• k — константа, равная

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной , радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

• Радиус вписанной окружности правильного восьмиугольника:

• Радиус описанной окружности правильного восьмиугольника:

• Площадь правильного восьмиугольника:

Через сторону восьмиугольника

Через радиус описанной окружности

Через апофему (высоту)

Площадь через квадрат[править | править код]

Площадь можно также вычислить как усечение квадрата

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

Тогда площадь равна:

Площадь через A (ширину восьмиугольника)

Ещё одна простая формула площади:

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

Два катета углового треугольника можно получить по формуле

Симметрия[править | править код]

Правильный восьмиугольник имеет группу симметрии Dih₈ порядка 16. Имеется 3 диэдральные подгруппы — Dih₄, Dih₂ и Dih₁, а также 4 циклические подгруппы — Z₈, Z₄, Z₂ и Z₁. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 ^[2]. Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

Примеры восьмиугольников по их симметриям

r16
d8	g8	p8
d4	g4	p4
d2	g2	p2
a1

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный^[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным^[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Разрезание правильного восьмиугольника[править | править код]

Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта ^[3].

Разрезание правильного восьмиугольника

На 6 ромбов

Тессеракт

Применение восьмиугольников[править | править код]

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии^[en]. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Другие использования[править | править код]

• 

  Зонты часто имеют восьмиугольную форму

• 

  Знаменитая восьмиугольная чашка с острова Белитунг

• 

Производные фигуры[править | править код]

Связанные многогранники[править | править код]

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

Усечённые гиперкубы

							…
Восьмиугольник	Усечённый куб	Усечённый тессеракт	Усечённый 5-куб	Усечённый 6-куб	Усечённый 7-куб	Усечённый 8-куб

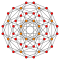
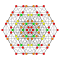
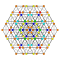
Восьмиугольник в качестве растянутого квадрата является первым в последовательности растянутых гиперкубов:

Расширенные гиперкубы

							…
Октаэдр	Ромбокубооктаэдр	Обструганный тессеракт	Обрубленный 5-куб	Пятиогранённый 6-куб	Шестиогранённый 7-куб	Семиогранённый 8-куб

См. также[править | править код]

• Восьмерик
• Восьмиугольное число
• Октаграмма
• Площадь Октогон в Будапеште, Венгрия
• Сглаженный восьмиугольник

Примечания[править | править код]

Литература[править | править код]

• У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
• Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google Архивная копия от 2 января 2016 на Wayback Machine  (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275—278. — ISBN 978-1-56881-220-5.

многоугольник с восемью сторонами

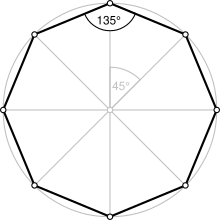Правильный восьмиугольник
Правильный восьмиугольник
Тип	Правильный многоугольник
Ребра и вершины	8
символ Шлефли	{8}, t {4}
диаграмма Кокстера	.
группа симметрии	двугранный (D8), порядок 2 × 8
Внутренний угол (градусов )	135 °
Двойной многоугольник	Собственный
Свойства	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрии, восьмиугольник (от греческого ὀκτάγωνον oktágōnon, “восемь angles ») представляет собой восьмиугольник многоугольник или 8-угольник.

A правильный восьмиугольник имеет символ Шлефли {8}, а также может быть построен как квазирегулярный усеченный квадрат, t {4}, в котором чередуются два типа ребер. Усеченный восьмиугольник, t {8} – это шестиугольник, {16}. 3D-аналог восьмиугольника может быть ромбокубооктаэдром с треугольными гранями на нем, как замененные ребра, если считать восьмиугольник усеченным квадратом (а это так).

Содержание

• 1 Свойства общего восьмиугольника
• 2 Правильный восьмиугольник
  • 2.1 Площадь
  • 2.2 Окружной радиус и внутренний радиус
  • 2.3 Диагонали
  • 2.4 Конструкция и элементарные свойства
  • 2.5 Стандартные координаты
  • 2.6 Рассечение
• 3 Наклон восьмиугольника
  • 3.1 Многоугольники Петри
• 4 Симметрия
• 5 Использование восьмиугольников
  • 5.1 Другое использование
• 6 Производные фигуры
  • 6.1 Связанные многогранники
• 7 См. Также
• 8 Ссылки
• 9 Внешние ссылки

Свойства общего восьмиугольника

Диагонали зеленого четырехугольника равны по длине и расположены под прямым углом друг к другу

Сумма всех внутренние углы любого восьмиугольника – 1080 °. Как и у всех многоугольников, внешние углы составляют 360 °.

Если квадраты построены полностью внутри или снаружи на сторонах восьмиугольника, то середины сегментов, соединяющих центры противоположных квадратов, образуют четырехугольник, который одновременно равнодиагонален и ортодиагональный (то есть диагонали которого равны по длине и расположены под прямым углом друг к другу).

восьмиугольник средней точки эталонного восьмиугольника имеет восемь вершин в средних точках сторон эталонного восьмиугольника. Если все квадраты построены внутри или снаружи на сторонах среднего восьмиугольника, то средние точки сегментов, соединяющих центры противоположных квадратов, сами образуют вершины квадрата.

Правильный восьмиугольник

A Правильный восьмиугольник представляет собой замкнутую фигуру со сторонами одинаковой длины и одинаковыми внутренними углами. Он имеет восемь линий отражательной симметрии и вращательной симметрии порядка 8. Правильный восьмиугольник представлен символом Шлефли {8}. Внутренний угол в каждой вершине правильного восьмиугольника равен 135 ° (3 π 4 { displaystyle scriptstyle { frac {3 pi} {4}}}радиан ). Центральный угол равен 45 ° (π 4 { displaystyle scriptstyle { frac { pi} {4}}}радиан).

Площадь

Площадь правильного восьмиугольника с длиной стороны a определяется как

A = 2 кроватки ⁡ π 8 a 2 = 2 (1 + 2) a 2 ≃ 4.828 a 2. { displaystyle A = 2 cot { frac { pi} {8}} a ^ {2} = 2 (1 + { sqrt {2}}) a ^ {2} simeq 4.828 , a ^ { 2}.}

С точки зрения радиуса описанной окружности R, площадь равна

A = 4 sin ⁡ π 4 R 2 = 2 2 R 2 ≃ 2,828 R 2. { displaystyle A = 4 sin { frac { pi} {4}} R ^ {2} = 2 { sqrt {2}} R ^ {2} simeq 2.828 , R ^ {2}.}

В терминах апофемы r (см. Также вписанный рисунок ) площадь

A = 8 tan ⁡ π 8 r 2 = 8 (2 – 1) г 2 ≃ 3,314 г 2. { displaystyle A = 8 tan { frac { pi} {8}} r ^ {2} = 8 ({ sqrt {2}} – 1) r ^ {2} simeq 3.314 , r ^ { 2}.}

Последние два коэффициента заключают в скобки значение pi, площадь единичной окружности .

область правильный восьмиугольник можно вычислить как усеченный квадрат.

Площадь также можно выразить как

A = S 2 – a 2, { displaystyle , ! A = S ^ {2} -a ^ {2},}

где S – длина восьмиугольника или вторая по длине диагональ; а – длина одной из сторон или оснований. Это легко доказать, если взять восьмиугольник, нарисовать квадрат снаружи (убедившись, что четыре из восьми сторон перекрываются с четырьмя сторонами квадрата), а затем взять угловые треугольники (это 45–45– 90 треугольников ) и размещает их прямыми углами внутрь, образуя квадрат. Края этого квадрата равны длине основания.

Учитывая длину стороны a, пролет S равен

S = a 2 + a + a 2 = (1 + 2) a ≈ 2,414 a. { displaystyle S = { frac {a} { sqrt {2}}} + a + { frac {a} { sqrt {2}}} = (1 + { sqrt {2}}) a приблизительно 2.414a.}

Тогда размах равен соотношению серебра, умноженному на сторону, a.

Тогда площадь будет такой, как указано выше:

A = ((1 + 2) a) 2 – a 2 = 2 (1 + 2) a 2 ≈ 4.828 a 2. { displaystyle A = ((1 + { sqrt {2}}) a) ^ {2} -a ^ {2} = 2 (1 + { sqrt {2}}) a ^ {2} приблизительно 4,828 a ^ {2}.}

Выраженная в размахе, площадь равна

A = 2 (2 – 1) S 2 ≈ 0,828 S 2. { displaystyle A = 2 ({ sqrt {2}} – 1) S ^ {2} приблизительно 0,828S ^ {2}.}

Другая простая формула для вычисления площади:

A = 2 a S. { displaystyle A = 2aS.}

Чаще известен промежуток S, и необходимо определять длину сторон a, как при разрезании квадратного куска материала на правильный восьмиугольник. Исходя из вышеизложенного,

a ≈ S / 2,414. { displaystyle a приблизительно S / 2.414.}

Две конечные длины e с каждой стороны (длины сторон треугольников (зеленые на изображении), усеченные из квадрата), а также e = a / 2, { displaystyle e = a / { sqrt {2}},}можно вычислить как

e = (S – a) / 2. { displaystyle , ! e = (Sa) / 2.}

Окружной радиус и внутренний радиус

Окружной радиус правильного восьмиугольника с точки зрения длины стороны a равен

R = (4 + 2 2 2) a, { displaystyle R = left ({ frac { sqrt {4 + 2 { sqrt {2}}}} {2}} right) a,}

и inradius равен

r = (1 + 2 2) a. { displaystyle r = left ({ frac {1 + { sqrt {2}}} {2}} right) a.}

(это половина отношения серебра умноженное на сторону, a, или половину размаха, S)

Диагонали

Правильный восьмиугольник с точки зрения длины стороны a имеет три различных типа диагоналей :

• Короткая диагональ;
• Средняя диагональ (также называемая размахом или высотой), которая в два раза больше внутреннего радиуса;
• Длинная диагональ, которая в два раза превышает длину окружного радиуса.

Формула для каждого из них следует из основных принципов геометрии. Вот формулы для их длины:

Конструкция и элементарные свойства

построение правильного восьмиугольника путем складывания листа бумаги

Правильный восьмиугольник по заданной описанной окружности может быть построен следующим образом:

1. Нарисуйте круг и диаметр AOE, где O – центр и A, E – точки на описанной окружности.
2. Нарисуйте еще один диаметр GOC, перпендикулярный AOE.
3. (Попутно обратите внимание, что A, C, E, G – вершины квадрата
4. Нарисуйте биссектрисы прямых углов GOA и EOG, образуя еще два диаметра HOD и FOB.
5. A, B, C, D, E, F, G, H – это диаметры вершины восьмиугольника.

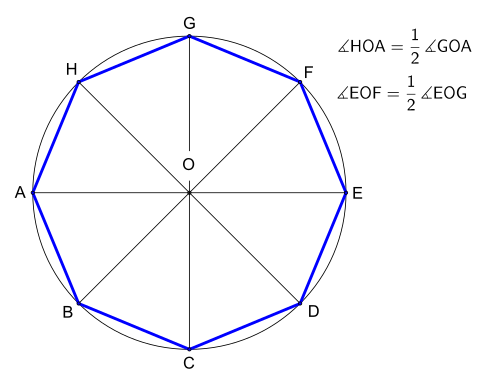восьмиугольник в заданной описанной окружности 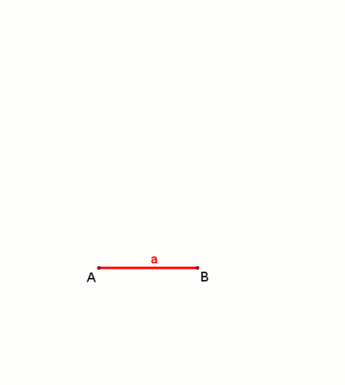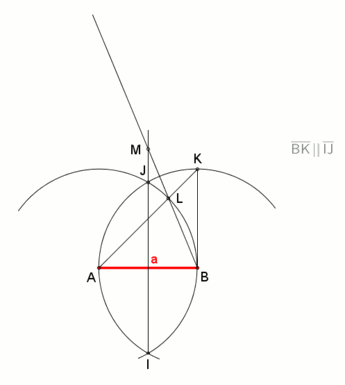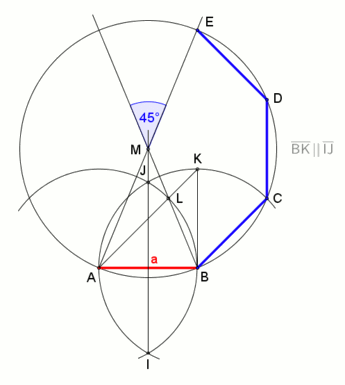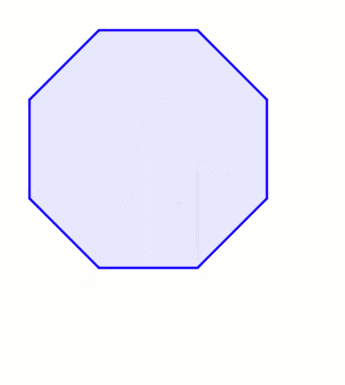восьмиугольник с заданной длиной стороны, анимация. (конструкция очень похожа на конструкцию шестиугольника с заданной длиной стороны.)

регулярный восьмиугольник можно построить с помощью линейки и компаса, так как 8 = 2, степень двойки :

Конструкция восьмиугольника Meccano uction.

Правильный восьмиугольник может быть построен из механических стержней. Нам нужно двенадцать стержней размера 4, три стержня размера 5 и два стержня размера 6.

Каждая сторона правильного восьмиугольника образует половину прямого угла в центре круга, соединяющего его вершины. Таким образом, его площадь можно вычислить как сумму 8 равнобедренных треугольников, что дает результат:

Площадь = 2 a 2 (2 + 1) { displaystyle { text {Area}} = 2a ^ {2} ({ sqrt {2}} + 1)}

для восьмиугольника со стороной a.

Стандартные координаты

Координаты вершин правильного восьмиугольника с центром в начале координат и длиной стороны 2:

• (± 1, ± (1 + √2))
• (± (1 + √2), ± 1).

Рассечение

8-кубовое проекция	Рассечение 24 ромба
	. Обычное	. Изотоксальное

Коксетер утверждает, что каждый зоногон (двухметровый угольник, противоположные стороны которого параллельны и равной длины) может быть разрезан на m (m-1) / 2 параллелограмма. В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Для правильного восьмиугольника m = 4, и его можно разделить на 6 ромбов, с одним примером, показанным ниже. Это разложение можно увидеть как 6 из 24 граней в плоскости проекции многоугольника Петри тессеракта . Список (последовательность A006245 в OEIS ) определяет количество решений как 8 по 8 ориентациям этого одного разреза. Эти квадраты и ромбы используются в мозаиках Амманна – Бенкера.

Рассеченный правильный восьмиугольник

. Тессеракт

. 4 ромба и 2 квадрата

Наклонный восьмиугольник

Правильный косой восьмиугольник, видимый как края квадратная антипризма, симметрия D 4d, [2,8], (2 * 4), порядок 16.

A наклонный восьмиугольник – это наклонный многоугольник с 8 вершинами и ребрами, но не находящихся в одной плоскости. Внутреннее пространство такого восьмиугольника в целом не определено. У косого зигзагообразного восьмиугольника вершины чередуются между двумя параллельными плоскостями.

A правильный скошенный восьмиугольник – это вершинно-транзитивный с равной длиной ребер. В 3-х измерениях это будет зигзагообразный восьмиугольник, который будет виден в вершинах и боковых гранях квадратной антипризмы с тем же D 4d, [2,8] симметрия, порядок 16.

многоугольники Петри

Правильный косой восьмиугольник – это многоугольник Петри для этих многомерных правильных и однородных многогранников, показанных в этих наклонных ортогональных проекциях из плоскостей A 7, B 4 и D 5Кокстера.

A7	D5	B4
. 7-симплекс	. 5-полукуб	. 16-элементный	. Тессеракт

Симметрия

Симметрия

11 симметрий правильного восьмиугольника. Линии отражений синие по вершинам, пурпурные по краям, а порядок вращения указан в центре. Вершины окрашены в соответствии с их положением симметрии.

Правильный восьмиугольник имеет симметрию Dih 8, порядок 16. Существует 3 двугранных подгруппы: Dih 4, Dih 2 и Dih 1. и 4 циклические подгруппы : Z 8, Z 4, Z 2 и Z 1, последнее подразумевает отсутствие симметрии.

Пример восьмиугольника по симметрии

. r16
. d8	. g8	. p8
. d4	. g4	. p4
. d2	. g2	. p2
. a1

На правильном восьмиугольнике существует 11 различных симметрий. Джон Конвей обозначает полную симметрию как r16 . Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины (d для диагонали) или ребра (p для перпендикуляров). Циклические симметрии в среднем столбце помечены как g за их приказы центрального вращения. Полная симметрия правильной формы – r16, симметрия не обозначена a1.

. Наиболее распространенными восьмиугольниками высокой симметрии являются p8, изогональный восьмиугольник, построенный из четырех зеркал. может чередовать длинные и короткие края, и d8, изотоксальный восьмиугольник, построенный с равными длинами ребер, но вершинами с чередованием двух разных внутренних углов. Эти две формы являются двойными друг другу и имеют половину порядка симметрии правильного восьмиугольника.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как направленные ребра.

Использование восьмиугольников

Восьмиугольный план этажа, Купол Скалы.

Восьмиугольная форма – это используется как элемент дизайна в архитектуре. Купол Скалы имеет характерный восьмиугольный план. Башня Ветров в Афинах – еще один пример восьмиугольной конструкции. Восьмиугольный план также использовался в церковной архитектуре, такой как Св. Георгия, Аддис-Абеба, Базилика Сан-Витале (в Равенне, Италия), Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий, Церковь Zum Friedefürsten (Германия) и ряд восьмиугольных церквей в Норвегии. Центральное пространство в Ахенском соборе, Каролингской Палатинской капелле, имеет правильную восьмиугольную планировку. Использование восьмиугольников в церквях также включает меньшие элементы дизайна, такие как восьмиугольная апсида Собора Нидарос.

Такие архитекторы, как Джон Эндрюс использовали восьмиугольную планировку этажей в зданиях для функциональное отделение офисных площадей от строительных служб, в частности, штаб-квартиры Intelsat в Вашингтоне, округ Колумбия, в Канберре, и офисов Octagon в Парраматта, Австралия.

Другое применение

• 

  Зонты часто имеют восьмиугольный контур.

• 

  Знаменитый ковер «Бухара» включает восьмиугольный мотив «слоновьей ноги».

• 

  План улиц и кварталов Барселоны в районе Эшампле основан на неправильных восьмиугольниках
• 

  Джангги использует восьмиугольные части.

• 

  Японские лотерейные автоматы часто имеют восьмиугольную форму.

• 

  Знак остановки, используемый в англоязычных странах, а также в большинстве европейских стран

• 

  Значок знака остановки с рукой посередине.

• 

  Триграммы Таоиста багуа часто расположены восьмиугольником

• 

  Знаменитая восьмиугольная золотая чаша с кораблекрушения Белитунг

• 

  Классы в Колледже Шимер традиционно хранятся вокруг восьмиугольных столов
• 

  Лабиринт Реймского собора квази-восьмиугольной формы.

• 

  Перемещение аналогового джойстика (ов) контроллера Nintendo 64, контроллера GameCube, Wii Nunchuk и Classic Controller ограничен вращающейся восьмиугольной областью, что позволяет ручке перемещаться только в восьми различных направлениях.

Производные числа

Родственные многогранники

восьмиугольник, как усеченный квадрат, является первым в последовательности усеченных гиперкубов :

Усеченных гиперкубов

Изображение								…
Имя	Восьмиугольник	Усеченный куб	Усеченный тессеракт	Усеченный 5-куб	Усеченный 6-кубик	Усеченный 7-кубический	Усеченный 8-кубический
Диаграмма Кокстера
Вершинная фигура	() v ()	. () v {}	. () v {3}	. () v {3,3}	() v {3,3,3}	() v {3,3,3,3}	() v {3,3,3,3,3}

Как развернутый квадрат, он также является первым в последовательность расширенных гиперкубов:

Расширенные гиперкубы

							…
восьмиугольник	Ромбокубооктаэдр	Бугристая тессера ct	Стерифицированный 5-куб	Пятиугольный 6-куб	Hexicated 7-кубический

См. также

Ссылки

Внешние ссылки

Найдите octagon в Викисловаре, бесплатном словаре.