Площадь отверстия с учетом времени опорожнения полусферического резервуара Калькулятор
| Search | ||
| Дом | физика ↺ | |
| физика | Механика жидкости ↺ | |
| Механика жидкости | Отверстия и мундштуки ↺ |
|
✖Радиус полусферического резервуара — это расстояние от центра полушария до любой точки полушария, называемое радиусом полушария.ⓘ Полусферический радиус резервуара [Rt] |
+10% -10% |
||
|
✖Начальная высота жидкости зависит от опорожнения резервуара через отверстие в его дне.ⓘ Начальная высота жидкости [Hi] |
+10% -10% |
||
|
✖Конечная высота жидкости зависит от опорожнения резервуара через отверстие в его дне.ⓘ Конечная высота жидкости [Hf] |
+10% -10% |
||
|
✖Общее время, затраченное телом, — это общее время, затрачиваемое телом на преодоление этого пространства.ⓘ Общее затраченное время [ttotal] |
+10% -10% |
||
|
✖Коэффициент расхода или коэффициент оттока представляет собой отношение фактического расхода к теоретическому расходу.ⓘ Коэффициент расхода [Cd] |
+10% -10% |
|
✖Площадь отверстия часто представляет собой трубу или трубку с различной площадью поперечного сечения, и ее можно использовать для направления или изменения потока жидкости (жидкости или газа).ⓘ Площадь отверстия с учетом времени опорожнения полусферического резервуара [a] |
⎘ копия |
Площадь отверстия с учетом времени опорожнения полусферического резервуара Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Полусферический радиус резервуара: 15 метр –> 15 метр Конверсия не требуется
Начальная высота жидкости: 24 метр –> 24 метр Конверсия не требуется
Конечная высота жидкости: 16 метр –> 16 метр Конверсия не требуется
Общее затраченное время: 80 Второй –> 80 Второй Конверсия не требуется
Коэффициент расхода: 0.94 –> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
3.32353524476575 Квадратный метр –> Конверсия не требуется
Кредиты

Технологический колледж ПСЖ
(PSGCT),
Коимбатур
Майаруцельван V создал этот калькулятор и еще 300+!

Инженерная школа Амрита
(ASE),
Валликаву
Санджай Кришна проверил этот калькулятор и еще 200+!
16 Отверстия и мундштуки Калькуляторы
Площадь отверстия с учетом времени опорожнения полусферического резервуара формула
Площадь отверстия = (pi*(((4/3)*Полусферический радиус резервуара*((Начальная высота жидкости^(3/2))-(Конечная высота жидкости^(3/2))))-((2/5)*((Начальная высота жидкости^(5/2))-(Конечная высота жидкости)^(5/2)))))/(Общее затраченное время*Коэффициент расхода*(sqrt(2*9.81)))
a = (pi*(((4/3)*Rt*((Hi^(3/2))-(Hf^(3/2))))-((2/5)*((Hi^(5/2))-(Hf)^(5/2)))))/(ttotal*Cd*(sqrt(2*9.81)))
Каков радиус полусферического резервуара?
Радиус полусферического резервуара – это расстояние от центра полусферы до любой точки полусферы, которое называется радиусом полусферы.
Что такое коэффициент расхода?
Коэффициент расхода определяется как отношение фактического расхода из отверстия к теоретическому расходу из отверстия.
Примеры гидравлических расчетов
Пример
7.1. Вода
вытекает из закрытого резервуара в
атмосферу через отверстие диаметром d
= 20
мм
и
коэффициентом расхода μ
= 0,62. Глубина погружения центра отверстия
h
= 0,45 м, избыточное давление на поверхности
жидкости p0и
= 8,3 кПа. Определить расход жидкости. Как
изменится избыточное давление для
пропуска того же расхода, если к отверстию
присоединить внешний насадок длиной l
= 0,1 м.
Решение:
Расход
при истечении жидкости через отверстие
определяется по формуле

где
 – расчетный напор,
– расчетный напор,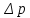 – перепад давления на отверстии (
– перепад давления на отверстии ( =
=
p0и,
т.к. за отверстием давление равно
атмосферному);
 – площадь отверстия.
– площадь отверстия.
Вычислим
расход воды через отверстие

Если
к отверстию в дне резервуара присоединить
цилиндрический насадок длиной l
того же диаметра, то формула примет
следующий вид

тогда
избыточное давление
 1830
1830
кПа
Пример
7.2. В
пароохладитель через трубку со сверлениями
поступает охлаждающая вода температурой
20°С расходом Q
= 0,00278 м3/с.
Давление воды в трубке p1
= 106
Па, давление в корпусе пароохладителя
p2
=
0,7×106
Па. Определить, сколько отверстий
диаметром d
= 0,003 м нужно просверлить в трубке для
обеспечения заданного расхода воды.
Решение:
Плотность
воды при температуре 20°С ρ
=
998,2 кг/м3
(табл.4.1), кинематический коэффициент
вязкости ν = 10-6
м2/с
(табл.4.5).
Определим
число Рейнольдса, характеризующее
истечение из отверстий:

По
графику (Приложение 8) определяем
коэффициент расхода отверстия μ = 0,6.
Расход
воды протекающей через одно отверстие,

Таким
образом, необходимое число отверстий

Пример
7.3. Определить
время опорожнения цистерны с мазутом
при следующих данных: объем мазута в
цистерне W
= 50 м3;
диаметр цистерны D
= 2,8 м; диаметр сливного патрубка d
= 0,1 м; кинематическая вязкость мазута
ν
= 0,69·10-4
м2/с.
Решение:
Для
определения времени опорожнения при
известном объеме наполнения резервуара
воспользуемся формулой

где

– площадь сливного патрубка; r
– радиус цистерны.
Коэффициент
расхода определим по графику в Приложении
9 в зависимости от числа Рейнольдса.
Число Рейнольдса определим по теоретической
скорости

в
начале истечения при Н = 2,8 м:

в
конце истечения при Н = 0,01 м:
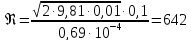
По
графику определяем, что соответствующие
коэффициенты расхода будут:
 (в начале истечения),
(в начале истечения), (в конце истечения).
(в конце истечения).
Принимая
для расчета среднее значение
 и подставляя его в формулу, получим:
и подставляя его в формулу, получим:
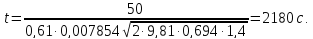
Методические рекомендации к проведению расчетов
Для
решения задач на истечение жидкости
через отверстие или насадок при заданном
коэффициенте расхода отверстия μ,
следует применить формулу (7.2), учитывая
при этом, что расчетный напор Н
складывается
из разности геометрических и
пьезометрических высот.
Для
определения площади проходного сечения,
скорости перемещения поршня, расхода
жидкости удобно использовать формулу
(7.3). При этом решение сводится к следующим
этапам:
-
определить
избыточное давление в рабочей полости; -
найти
разность давлений Δр
на отверстии; -
записать
уравнение расхода жидкости, вытесняемой
поршнем; -
выразить
неизвестную величину.
Если
по условию задачи не задан коэффициент
расхода, то для его определения необходимо
использовать график (Приложение 9). С
этой целью нужно
1)
определить число Рейнольдса по
теоретической скорости (см. пример 7.3);
2)
по графику найти точку на графике
зависимости μ
= f(Re)
и определить соответствующее ей значение
коэффициента расхода μ.
Задачи
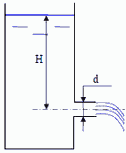
Задача
7.1.
Определить
напор в баке, если расход воды при
истечении через цилиндрический насадок
диаметром d
= 0,05 м составляет Q
= 0,05 м3/с.
Истечение происходит при постоянном
напоре.
Задача
7.2. Определить
расход жидкости (ρ
= 800 кг/м3),
вытекающей из бака через отверстие
площадью S0
= 1 см2.
Показание ртутного прибора, измеряющего
давление воздуха, h
= 268 мм, высота
H0
= 2 м,
коэффициент расхода отверстия µ
= 0,60.
Задача
7.3. Из отверстия
диаметром d
= 0,4 см в тонкой стенке резервуара вытекает
вода, имеющая температуру t
= 18 ℃;.
Отверстие расположено на высоте h
= 8 м над поверхностью земли. Постоянный
напор воды в резервуаре H
= 6 м. Определить расход и скорость
истечения, а также расстояния x,
на котором струя коснется поверхности
земли.
Задача
7.4. Жидкость
плотностью ρ
= 850 кг/м3
вытекает через установленный на боковой
поверхности закрытого резервуара
цилиндрический насадок диаметром d
= 6 см. Избыточное давление на свободной
поверхности жидкости pизб
= 6,1 кПа, расход жидкости Q
=5 л/с, глубина
погружения насадка h
= 90 см. Определить коэффициент расхода
насадка.

Задача
7.5. Определить
направление истечения жидкости (ρ
= ρвод)
через отверстие d0
= 5 мм и
расход, если разность уровней H
= 2 м, показание вакуумметра рвак
соответствует 147 мм.рт.ст., показание
манометра рм
= 0,25 МПа,
коэффициент расхода
μ = 0,62.
Задача
7.6. Определить
расход и скорость воды при истечении
из круглого отверстия диаметром d
= 0,065 м в тонкой стенке и установить, как
они изменяются, если к этому отверстию
присоединить цилиндрический насадок
длиной l
= 4d.
Напор в центре тяжести отверстия H
= 2,8 м.

Задача
7.7.
Определить
объем воды V,
налитой в цилиндрический бак диаметром
D =
0,8 м, если вся вода вытекла из бака через
отверстия в дне диаметром d
= 100 мм за
время t
= 60 c. Какое время t1
потребуется для опорожнения такого же
объема воды, если уменьшить диаметр
бака в полтора раза?
Задача
7.8. Определить
время полного опорожнения открытого
резервуара с постоянной площадью сечения
Ω объемом V
= 50 л через отверстие в дне при начальном
расходе Q
= 1,8 м3/ч
и напоре H
= 0,5 м.
Задача
7.9. Время
частичного опорожнения вертикально
расположенного цилиндрического открытого
бака через донное отверстие в тонкой
стенке составило t
= 40 с. За это
время уровень жидкости изменился от
h1
= 2 м до h2
= 1 м. Определить диаметр отверстия, если
диаметр бака D
= 0,5 м.
Задача
7.10. Определить
первоначальный уровень в резервуаре
h1,
если время частичного опорожнения
открытого резервуара через донное
отверстия до уровня h2
= 0,7 м равно t
= 70 с. Диаметр отверстия d
= 0,05 м. Размеры поперечного сечения
резервуара постоянные a
х b
= 0,8 х 0,7.
Задача
7.11. Открытый
резервуар опоражнивается через
коноидальный насадок диаметром d
= 5 см. Определить площадь поперечного
сечения резервуара, если напор воды за
время t
= 2 мин понизился на ΔH
= 5 см и стал равным H
= 35 см. Насадок присоединен к боковой
поверхности резервуара.
Задача
7.12. Открытый
резервуар с вертикальными стенками
опоражнивается через внешний цилиндрический
насадок диаметром d
= 2,5 см. Через 35 с напор составил H
= 1,5 см. Определить расход в начальный
момент времени, если площадь поперечного
сечения резервуара Ω = 1,75 м2.
Насадок присоединен к отверстию на
боковой стенке резервуара. 
Задача
7.13. Определить
время наполнения мерного бака объемом
V
= 0,02 м3,
если истечение происходит при постоянном
уровне воды, через внешний цилиндрический
насадок диаметром d
= 0,02 м при
избыточном давлении на поверхности
воды p0изб
= 30 кПа. Глубина погружения насадка h
= 2,4 м.
Задача
7.14. Определить
расход воды через отверстие диаметром
d
= 0,08 м, коэффициент расхода которого μ
= 0,65, если
показание манометра pизб
= 150 кПа, а высота установки манометра
над осью отверстия h
= 1,5 м.

Задача
7.15. Газ,
заполняющий вертикальную трубу, вытекает
в атмосферу через два насадки диаметром
d =
10 мм, расположенные по высоте трубы на
расстоянии a
= 100 м друг от друга. Коэффициент расхода
насадков (с учетом сопротивления
подводящих горизонтальных трубок) μ
= 0,95.
Определить
массовый расход M
газа через каждый насадок, если показание
спиртового манометра, присоединенного
к трубке у нижнего насадка, h
= 200 мм (плотность спирта ρсп
= 800 кг/м3).
Давление
атмосферного воздуха на уровни нижнего
насадка pат
= 100 кПа, температура воздуха и газа t
= 20 ℃.
Значения удельной газовой постоянной
воздуха Rв
= 287 Дж/(кг·К) и газа Rг
= 530 Дж/(кг·К).
Скоростным
напором и потерями в трубе пренебречь,
плотность воздуха и газа принимать
постоянными по высоте a.
Задача
7.16. Два
резервуара с избыточным давлением p0и1
= 105
Па и p0и2
= 0,6·105
Па соединены между собой короткой трубой
диаметром d
= 20 мм. Определить расход воды в трубе,
если h1
= 0,5 м до h2
= 1,4 м.
Задача
7.17. Определить
коэффициенты расхода, скорости, сжатия
при истечении воды в атмосферу через
отверстие диаметром d
= 10 мм под напором H
= 2 м, если расход Q
= 0,294 л/с, дальность полета струи l
= 3 м. Отверстие расположено на высоте h
= 1,2 м от пола.
Задача
7.18.
Из открытого бака вытекает вода через
малое отверстие в атмосферу. Глубина
воды в баке h
= 3 м поддерживается постоянной. При
какой высоте h1
отверстия от пола дальность падения
струи l
будет максимальной.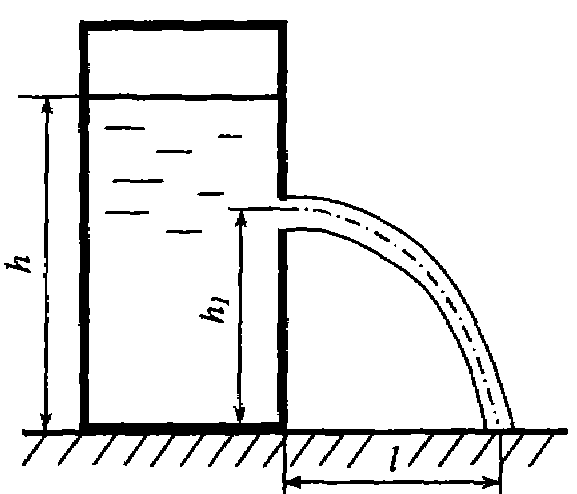
Задача
7.19. Для задачи
4.18 определить, при какой глубине бака
дальность полета будет максимальной,
если отверстие расположено на высоте
h1
= 1,5 м от основания.
Задача
7.20. Мазут
подается в топку котла с расходом Qм
= 100 кг/ч. Для сжигания мазута (ρм
= 850 кг/м3)
требуется воздух (ρв
= 850 кг/м3)
в количестве V
= 8,7 м3/кг.
Определить необходимые диаметры каналов
для подачи воздуха и мазута, если мазут
подается под давлением pи
= 2,5 кгс/см2,
а воздух под давлением 200 мм рт.ст.
Коэффициенты скорости и расхода принять
φ
= μ
= 0,82.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Главная страница
Содержание
Введение
Основы гидростатики
Основы гидродинамики
Гидравлические сопротивления
Истечние жидкости из отверстий, насадков и из-под затворов
Гидравлический расчет простых трубопроводов
Гидравлические машины
Лекция 5. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, НАСАДКОВ И ИЗ-ПОД ЗАТВОРОВ
Рассмотрим различные случаи истечения жидкости из резервуаров, баков, котлов через отверстия и насадки
(коротки трубки различной формы) в атмосферу или пространство, заполненное газом или той же жидкость. В
процессе такого истечения запас потенциальной энергии, которым обладает жидкость, находящаяся в резервуаре,
превращается в кинетическую энергию свободной струи.
Основным вопросом, который интересует в данном случае, является определение скорости истечения и
расхода жидкости для различных форм отверстий и насадков.
Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое
отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рис.5.1).
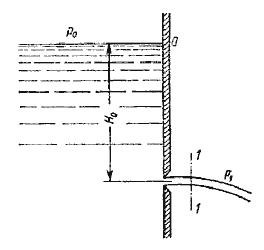
Рис. 5.1. Истечение из резервуара через малое отверстие
Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму,
показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или
имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с
внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие
обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке,
к осевому движению в струе.
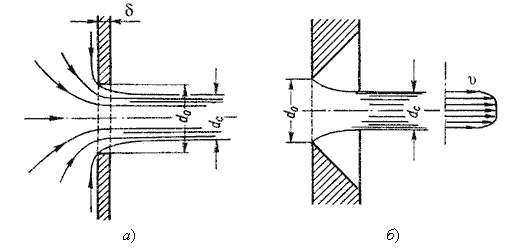
Рис. 5.2. Истечение через круглое отверстие
Степень сжатия оценивается коэффициентом сжатия.
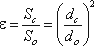
где Sс и Sо – площади поперечного сечения струи и отверстия
соответственно; dс и dо – диаметры струи и отверстия соответственно.
Скорость истечения жидкости через отверстие такое отверстие
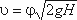
где Н – напор жидкости, определяется как
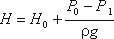
φ- коэффициент скорости
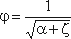
где α – коэффициент Кориолиса;
ζ- коэффициент сопротивления отверстия.
Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь
сечения:
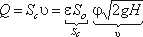
Произведение ε и φ принято обозначать буквой и называть коэффициентом
расхода, т.е. μ = εφ.
В итоге получаем расход
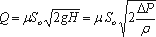
где ΔР – расчетная разность давлений, под действием которой происходит истечение.
При помощи этого выражения решается основная задача – определяется расход.
Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого
отверстия можно определить по эмпирически построенным зависимостям. На рис.5.3 показаны зависимости
коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости
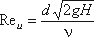
где ν – кинематическая вязкость.
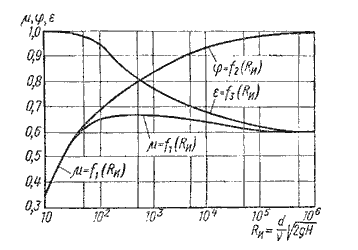
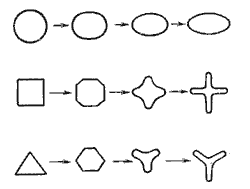
| Рис. 5.3. Зависимость ε, φ и от числа Reu | Рис. 5.4. Инверсия струй |
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее
длине, называемое инверсией струи (рис.5.4). Обуславливается это явление в основном действием сил
поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру
отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на
формирование струи оказывает влияние близость боковых стенок резервуара (рис.5.5).
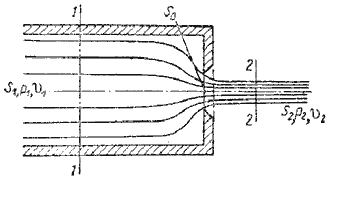
Рис. 5.5. Схема несовершенного сжатия струи
Так как боковые стенки частично направляют движение жидкости при подходе к отверстию, то струя по выходе
из отверстия сжимается в меньшей степени, чем из резервуара неограниченных размеров, как это было описано в
п.5.1.
При истечении жидкостей из цилиндрического резервуара круглого сечения через круглое отверстие,
расположенное в центре торцевой стенки, при больших числах Re коэффициент сжатия для идеальной жидкости можно
найти по формуле, представленной Н.Е. Жуковским:
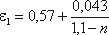
где n – отношение площади отверстия Sо к площади поперечного сечения
резервуара S1
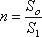
Расход жидкости при несовершенном сжатии
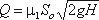
где напор Н нужно находить с учетом скоростного напора в резервуаре
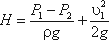
Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же
жидкостью (рис.5.6). такой случай называется истечением под уровень, или истечением через затопленное
отверстие.
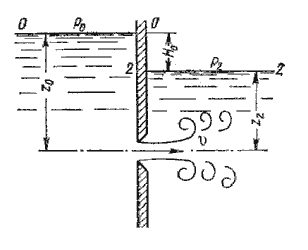
Рис. 5.6. Истечение по уровень
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Скорость истечения в сжатом сечении струи
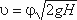
где φ – коэффициент скорости;
Н – расчетный напор,
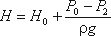
Расход жидкости равен
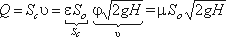
Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор
Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость
и расход жидкости в данном случае не зависят от высот расположения отверстия.
Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в
воздушную среду.
Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без
закругления входной кромки (рис. 5.7). На практике такой насадок часто получается в тех случаях, когда
выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в
газовую среду может происходить в двух режимах.
Первый режим – безотрывный режим. При истечении струя, после входа в насадок сжимается примерно
так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров
отверстия из насадка выходит полным сечением (рис.5.7).
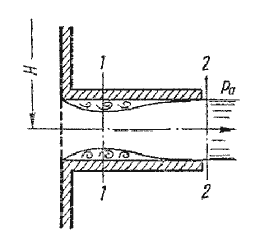
Рис. 5.7. Истечение через насадок
Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа
Рейнольдса, определяется по эмпирической формуле:
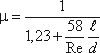
Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия
ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.
Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадком 2-2 и
преобразовать его, то можно получить падение давления внутри насадка
P2 – P1  0,75Hgρ
0,75Hgρ
При некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение
1-1) становится равным нулю (P1 = 0), и поэтому
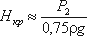
Следовательно, при Н > Нкр давление P1 должно было бы стать
отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится
невозможным. Поэтому при Н  Нкр происходит изменение режима истечения, переход от первого
Нкр происходит изменение режима истечения, переход от первого
режима ко второму (рис.5.8).
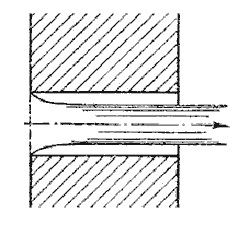
Рис. 5.8. Второй режим истечения через насадок
Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую
форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же,
как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от
первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.
При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от
описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается
кавитационный режим.
Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме – большое
сопротивление и недостаточно высокий коэффициент расхода, а на втором – очень низкий коэффициент расхода.
Недостатком также является возможность кавитации при истечении под уровень.
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или
устройства конического входа. На рис.5.9 даны различные типы насадков и указаны значения соответствующих
коэффициентов.

Рис. 5.9. Истечение жидкости через насадки а – расширяющиеся конические; б – сужающиеся
конические; в – коноидальные; г – внутренние цилиндрические
Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную
струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.).
Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором
течение является неустановившемся (рис.5.10).
Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент
времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.
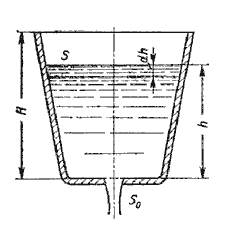
Рис. 5.10. Схема опорожнения резервуара
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом
уровне S, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt,
можно записать следующее уравнение объемов:
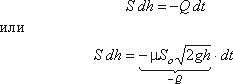
где dh – изменение уровня жидкости за время dt.
Отсюда время полного опорожнения сосуда высотой Н
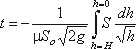
Если будет известен закон изменения площади S по высоте h, то интеграл можно
подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного
опорожнения
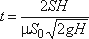
Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза
больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 5.12)
выразим зависимость переменной площади S от h:
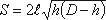
где l – длина цистерны; D – диаметр цистерны.
Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D
до h2 = 0, получится равным
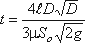
Во многих водозаборных и водопропускных гидротехнических сооружениях расходы воды проходят через отверстия,
перекрываемые затворами. Затворы поднимают на определенную высоту над дном и пропускают через отверстия
необходимые расходы. Чаще всего на гидромелиоративных сооружениях устраивают отверстия прямоугольного сечения,
истечение из которых и рассмотрим.
Отверстия могут быть незатопленными (истечение свободное) и затопленными, когда уровень воды за затвором
влияет на истечение.
Если отверстие незатопленное, то вытекающая из-под затвора струя находится под атмосферным давлением
(рис. 5.13). При истечении через затопленное отверстие струя за затвором находится под некоторым слоем воды
(рис. 5.14).
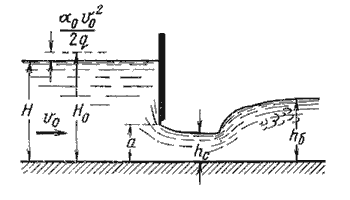
Рис. 5.13. Истечение из-под затвора через незатопленное отверстие
Когда затвор приподнят над дном, вытекающая из-под него струя испытывает сжатие в вертикальной плоскости.
На расстоянии, примерно равном высоте отверстия а (высоте поднятия затвора), наблюдается наиболее
сжатое сечение. Глубина в сжатом сечении hc связана с высотой отверстия а следующей
зависимостью:
hc = ε’a
где ε’ – коэффициент вертикального сжатия струи.
Коэффициент вертикального сжатия ε’ зависит от отношения высоты отверстия а
к напору (глубине воды перед затвором) Н. Для ориентировочных расчетов можно принимать
ε’ = 0,64.
Если составить уравнение Бернулли для сечений, проведенных перед затвором и в сжатом сечении, после
преобразований получим:
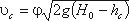
где φ – коэффициент скорости,
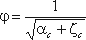
где Н0 – напор с учетом скорости подхода,
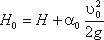
Тогда расход при истечении из-под затвора при незатопленном отверстии определится по формуле:
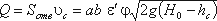
где S – площадь отверстия, S = ab.
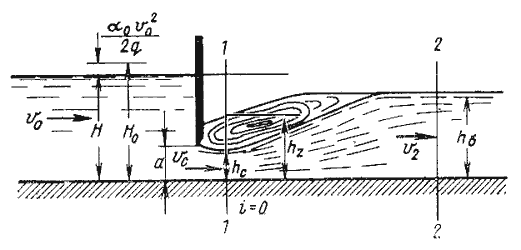
Рис. 5.14. Истечение из-под затвора при затопленном отверстии
При истечении через затопленное отверстие (рис. 5.14) расход определится по формуле:
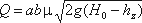
где hz – глубина в том сечении, где наблюдается максимальное сжатие истекающей из-под
затвора струи.
Глубина hz определяется из зависимости
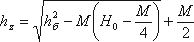
в которой
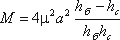
а hб – глубина в отводящем канале (бытовая глубина).
Если вытекающая из отверстия или насадка струя попадает на неподвижную стенку, то она с определенным
давлением воздействует на нее. Основное уравнение, по которому вычисляется давление струи на площадку,
имеет вид
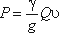
На рис. 5.15 приведены наиболее часто встречающиеся в практике ограждающие поверхности (преграды) и
уравнения, по которым вычисляется давление струи на соответствующую поверхность.
Величина давления струи, естественно, зависит от расстояния насадка до преграды. С увеличением расстояния
струя рассеивается и давление уменьшается. Соответствующие исследования показывают, что в данном случае
струя может быть разбита на три характерные части: компактную, раздробленную и распыленную (рис.5.16).
В пределах компактной части сохраняется цилиндрическая форма струи без нарушения сплошности движения.
В пределах раздробленной части сплошность потока нарушается, причем струя постепенно расширяется. Наконец,
в пределах распыленной части струи происходит окончательный распад потока на отдельные капли.
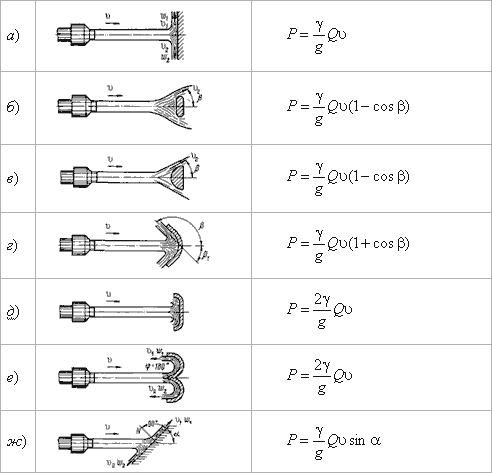
Рис. 5.15. Взаимодействие струи жидкости с неподвижной поверхностью
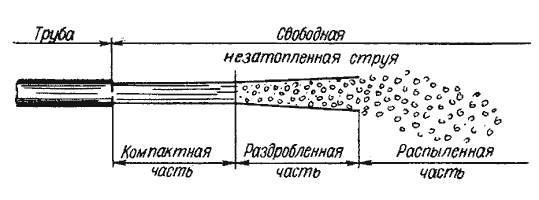
Рис. 5.16. Составные части свободной струи
Проверить себя ( Тест )
Наверх страницы
Истечние жидкости из отверстий, насадков и из-под затворов
Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же
жидкостью (рис.5.6). такой случай называется истечением под уровень, или истечением через затопленное
отверстие.
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор
Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость
и расход жидкости в данном случае не зависят от высот расположения отверстия.
Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в
воздушную среду.
5.4. Истечение через насадки при постоянном напоре
Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без
закругления входной кромки (рис.
5.7). На практике такой насадок часто получается в тех случаях, когда
выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в
газовую среду может происходить в двух режимах.
Первый режим — безотрывный режим. При истечении струя, после входа в насадок сжимается примерно
так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров
отверстия из насадка выходит полным сечением (рис.5.7).
Рис. 5.7. Истечение через насадок
Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа
Рейнольдса, определяется по эмпирической формуле:
Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия
ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.
Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадком 2-2 и
преобразовать его, то можно получить падение давления внутри насадка
P2 — P1 0,75Hgρ
При некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение
1-1) становится равным нулю (P1 = 0), и поэтому
Следовательно, при Н > Нкр давление P1 должно было бы стать
отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится
невозможным. Поэтому при Н Нкр происходит изменение режима истечения, переход от первого
Поэтому при Н Нкр происходит изменение режима истечения, переход от первого
режима ко второму (рис.5.8).
Рис. 5.8. Второй режим истечения через насадок
Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую
форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же,
как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от
первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.
При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от
описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается
кавитационный режим.
Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме — большое
сопротивление и недостаточно высокий коэффициент расхода, а на втором — очень низкий коэффициент расхода.
Недостатком также является возможность кавитации при истечении под уровень.
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или
устройства конического входа. На рис.5.9 даны различные типы насадков и указаны значения соответствующих
коэффициентов.
Рис. 5.9. Истечение жидкости через насадки а — расширяющиеся конические; б — сужающиеся
конические; в — коноидальные; г — внутренние цилиндрические
Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную
струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.).
Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.
5.5. Истечения через отверстия и насадки при переменном напоре
(опорожнение сосудов)
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором
течение является неустановившемся (рис. 5.10).
5.10).
Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент
времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.
Рис. 5.10. Схема опорожнения резервуара
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом
уровне S, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt,
можно записать следующее уравнение объемов:
где dh — изменение уровня жидкости за время dt.
Отсюда время полного опорожнения сосуда высотой Н
Если будет известен закон изменения площади S по высоте h, то интеграл можно
подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного
опорожнения
Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза
больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.
Лекции Основы гидравлики — Стр 4
-
искривлением
линий тока; -
изменением
величины скорости вследствие уменьшения
или увеличения живых сечений; -
отрывом
транзитных струй от поверхности,
вихреобразованием.
Несмотря
на многообразие местных сопротивлений,
в большинстве из них изменение скоростей
движения приводит к возникновению
вихрей, которые для своего вращения
используют энергию потока жидкости
(см. рисунок 3.21, б).
Таким
образом, основной причиной гидравлических
потерь напора в большинстве местных
сопротивлений является вихреобразование.
Практика показывает, что эти потери
пропорциональны квадрату скорости
жидкости, и для их определения используется
формула Вейсбаха
.
При
вычислении потерь напора по формуле
Вейсбаха наибольшей трудностью является
определение безразмерного коэффициента
местного сопротивления
.
Из-за сложности процессов, происходящих
в местных гидравлических сопротивлениях,
теоретически найти
удается
только в отдельных случаях, поэтому
большинство значений этого коэффициента
получено в результате экспериментальных
исследований.
Рассмотрим способы
определения коэффициента
для
наиболее распространенных местных
сопротивлений при турбулентном режиме
течения.
Для внезапного расширения
потока (см. рисунок 3.21, б)
имеется
теоретически полученная формула Борда
для коэффициента
,
который однозначно определяется
соотношением площадей до расширения
(S1)
и
после него (S2):
.
(3.35)
Следует отметить частный случай,
когда жидкость вытекает из трубы в бак,
т. е. когда площадь сечения потока в
трубе S1
значительно
меньше таковой в баке
S2.
Тогда
из формулы (3.35) следует, что для выхода
трубы в бак
=
1. Для оценки коэффициента потерь напора
при внезапном сужении
используется
эмпирическая формула, предложенная
И.Е. Идельчиком, которая также учитывает
соотношение площадей до расширения
(S1)
и
после него (S2):
.
(3.36)
Для внезапного сужения потока
тоже необходимо отметить частный случай,
когда жидкость вытекает из бака по
трубе, т. е. когда площадь сечения потока
е. когда площадь сечения потока
в трубе S2
значительно
меньше таковой в баке S1.
Тогда
из (3.36) следует, что для входа трубы в
бак
=
0,5.
В
гидравлических системах достаточно
часто встречаются плавное расширение
потока (рисунок 3.21, в)
и
плавное сужение потока (рисунок 3.21, г).
Расширяющееся русло в гидравлике принято
называть диффузором, а сужающееся —
конфузором. При этом, если конфузор
выполнен с плавными переходами в сечениях
1‘-1‘
и
2‘-2‘,
то его называют соплом. Эти местные
гидравлические сопротивления могут
иметь (особенно при малых углах α)
достаточно большой длины l.
Поэтому кроме потерь из-за вихреобразования,
вызванного изменением геометрии потока,
в этих местных сопротивлениях учитывают
потери напора на трение по длине.
Значения
коэффициентов для плавного расширения
и
плавного сужения
находят
с введением поправочных коэффициентов
в формулы (3.35) и (3.36):
и
.
Поправочные
коэффициенты kp
и
kc
имеют
численные значения меньше единицы,
зависят от углов α, а также от плавности
переходов в сечениях и 1‘-1‘
и
2‘-2‘.
Их
значения приводятся в справочниках.
Весьма
распространенными местными сопротивлениями
являются также повороты потоков. Они
могут быть с внезапным поворотом трубы
(рисунок 3.21,
д)
или
с плавным поворотом (рисунок 3.21,
е).
Внезапный
поворот трубы (или колено) вызывает
значительные вихреобразования и поэтому
приводит к существенным потерям напора.
Коэффициент сопротивления колена
определяется
в первую очередь углом поворота δ и
может быть выбран из справочника.
Плавный
поворот трубы (или отвод) существенно
снижает вихреобразование и, следовательно,
потери напора. Коэффициент
для
данного сопротивления зависит не только
от угла поворота δ, но и от относительного
радиуса поворота R/d
. Для
определения коэффициента
существуют
различные эмпирические зависимости,
например,
,
(3.37)
либо находятся в справочной
литературе.
Коэффициенты потерь
других местных сопротивлений, встречающихся
в гидравлических системах, также могут
быть определены по справочнику.
3.11 Местные сопротивления при больших
и малых числах Рейнольдса.
Метод
эквивалентной длины
Ранее
были рассмотрены местные гидравлические
сопротивления, потери напора в которых
пропорциональны квадрату скорости
или расхода. Однако квадратичный характер
зависимости потерь — наиболее
распространенный, но все же частный
случай для местного сопротивления.
В
Рисунок
3.22 — Схема жиклера
машиностроительных
гидросистемах встречаются местные
сопротивления, внутри которых имеет
место ламинарное течение. Потери
напора в таких сопротивлениях
пропорциональны скорости (или
расходу) в первой степени, т.е. носят
линейный характер. Кроме того, при
ламинарном течении жидкости в трубах
коэффициенты местных сопротивлений не
всегда остаются постоянными. Указанные
сопротивления встречаются существенно
реже, чем сопротивления с квадратичной
зависимостью потерь, и не имеют
определяющего значения, но при расчете
отдельных гидросистем их необходимо
учитывать.
В качестве примера
рассмотрим жиклер (рисунок 3. 21), в канале
21), в канале
которого существует ламинарное течение.
Потери напора в жиклере будут складываться
из потерь на трение в канале и потерь
на внезапное расширение потока при
выходе из этого канала. Причем первый
вид из указанных потерь будет пропорционален
скорости в первой степени (так как в
канале ламинарное течение), а второй —
квадрату скорости (потери на
вихреобразование).
Если принимать
во внимание оба вида потерь, то формула
для коэффициента сопротивления жиклера
будет иметь вид
.
(3.38)
Это общее выражение для
коэффициента любого местного сопротивления.
Первое слагаемое в (3.38) учитывает линейные
потери, а второе — квадратичные. Соотношение
между первым и вторым слагаемыми зависит
от геометрических размеров каждого
конкретного сопротивления.
Использование
зависимости (3.38) приводит к значительному
усложнению при расчетах гидравлических
систем. Однако практика показывает, что
в подавляющем большинстве местных
сопротивлений один из видов потерь
существенно превышает второй, поэтому
при проведении реальных расчетов одним
из слагаемых формулы (3.
4 ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И
НАСАДКИ
4.1
Истечение через отверстие в тонкой
стенке
Рассмотрим
истечение жидкости через отверстие
диаметром d0
в
стенке бака, расположенное на глубине
Н0,
в газовую среду с некоторым давлением
р1
(рисунок 4.1, a).
При этом предполагается, что если
отверстие мало по сравнению с размерами
бака и глубиной Н0,
то другие стенки бака и свободная
поверхность жидкости не влияют на приток
жидкости к отверстию.
Характер
истечения в этом случае показан на
рисунке 4.1, б.
Частицы
жидкости приближаются к отверстию из
всего близлежащего объема, двигаясь по
различным траекториям. Некоторые из
них при попадании в отверстие должны
изменить направление своего движения
на 90°. Так как каждая частица имеет
массу, то мгновенно изменить направление
своего движения она не может. Следствием
этого является сжатие струи жидкости
при истечении. Процесс сжатия струи
Процесс сжатия струи
практически завершается на расстоянии,
равном примерно одному диаметру
отверстия, и после этого струя приобретает
цилиндрическую форму с диаметром
поперечного сечения dc.
Точно
такими же будут условия истечения, если
отверстие выполнено в толстой стенке
со снятием фаски с внешней
стороны.
Рисунок
4.1 — Схемы истечения жидкости через
отверстие в тонкой стенке в газовую
среду (а)
и формирование струи (б)
Степень
сжатия струи оценивается коэффициентом
сжатия ε,
равным отношению площади поперечного
сечения струи к площади отверстия
.
(4.1)
Определим расход Q
жидкости через рассматриваемое отверстие.
Для этого запишем уравнение Бернулли
для двух сечений (см. рисунок 4.1, а):
сечения
0-0
и
сечения
1-1.
Сечение
0-0
— это
открытая поверхность жидкости в
баке, следовательно, в нем давление р0,
а скорость жидкости можно считать равной
нулю. Сечение 1-1
струи
должно быть выбрано в той ее части, где
струя уже приняла цилиндрическую форму;
тогда в этом сечении давление равно
давлению р1
окружающей
среды. Если в качестве плоскости сравнения
Если в качестве плоскости сравнения
выбрать горизонтальную плоскость,
проходящую через ось отверстия, то
получим
,
где
α — коэффициент Кориолиса, учитывающий
неравномерность распределения скорости
по сечению 1—1
струи;
—
средняя скорость жидкости в сечении
1—1;
—
коэффициент сопротивления отверстия,
учитывающий торможение частиц жидкости
о входную кромку отверстия.
Перенесем
первое слагаемое правой части уравнения
в левую часть и обозначим ее как расчетный
напор
,
тогда
;
отсюда
средняя скорость истечения жидкости
,
(4.2)
где
—
безразмерная величина, получившая
название коэффициент
скорости и
определяемая по формуле
.
(4.3)
В случае истечения идеальной
жидкости (α = 1 и
=
0) из формулы (4.3) следует, что
=
1, т.е. скорость истечения идеальной
жидкости
.
(4.4)
Таким образом, на основании
сравнения формул (4.3) и (4.4) можно
сформулировать физический смысл
коэффициента скорости
.
Это величина, равная отношению средней
скорости истечения реальной жидкости
к скорости истечения идеальной жидкости
в тех же условиях. Очевидно, что при
Очевидно, что при
истечении реальной жидкости коэффициент
всегда
меньше единицы.
Расход Q
при
истечении определим как произведение
средней скорости истечения реальной
жидкости и фактической площади живого
сечения струи. Используя формулы (4.1) и
(4.3), получим
.
Произведение
двух безразмерных коэффициентов
и
принято
называть коэффициентом
расхода и
обозначать
.
(4.5)
Тогда
.
(4.6)
Из (4.6) следует, что
Таким
образом, физический смысл коэффициента
расхода
состоит
в том, что он численно равен отношению
действительного расхода Q
при
истечении жидкости к тому расходу Qu,
который имел бы место при отсутствии
сжатия струи и сопротивления
истечению.
Следует обратить внимание
на то, что Qu
не
является расходом при истечении идеальной
жидкости, так как идеальная жидкость
отличается от реальной только отсутствием
вязкости. Эффект же сжатия струи при
истечении идеальной жидкости, связанный
с инерционными свойствами частиц
жидкости, в условиях отсутствия трения
проявляется в еще большей степени.
На
практике формула (4.6) используется
достаточно редко из-за сложностей,
возникающих при определении расчетного
напора Hр,
особенно в закрытых гидросистемах.
Поэтому сделаем следующие преобразования.
Обозначим внутри бака на уровне оси
отверстия на некотором удалении от него
(где скорость жидкости можно принять
равной нулю) давление
(см.
рисунок 4.1, а),
тогда
перепад давления Δр,
под действием которого происходит
истечение жидкости через отверстие,
запишется в виде
.
Выразив
из этой формулы напор Hp
и
подставив его в формулу (4.6), получим
.
(4.7)
При помощи формулы (6.7) решается
основная задача — определение расхода
жидкости при истечении. Она широко
применяется при расчетах элементов
машиностроительных гидросистем.
Таким
образом, нами введены в рассмотрение
три коэффициента —
,
и
,
характеризующие процесс истечения
жидкости. Все они являются функцией
числа Рейнольдса Re. Однако для маловязких
жидкостей (воды, бензина и др.), истечение
которых, как правило, происходит при
больших значениях Re, эти коэффициенты
практически постоянны:
=
0,64;
=
0,97;
=
0,62.
4.2 Истечение под уровень
При
течении жидкости в закрытых руслах
часто приходится иметь дело с истечением
жидкости не в газовую среду, а в
пространство, заполненное этой же
жидкостью (рисунок 4.2). Такое истечение
называется истечением под уровень или
истечением через затопленное
отверстие.
Здесь, так же как и в
предыдущем случае, при определении
расхода Q
следует
составить уравнение Бернулли. Запишем
его для сечений 1-1
и 2-2, в
которых скорости движения жидкости
принимаются равными нулю:
Рисунок
4.2 – Схема истечения жидкости через
отверстие в тонкой стенке под уровень
,
где
—
потери напора при движении жидкости
между сечениями 1-1
и 2-2.
При
определении потерь напора в этом случае
необходимо учитывать, что они складываются
из двух составляющих:
,
где
ho
— потери напора на торможение частиц
жидкости о входную кромку отверстия;
hв.р
— потери напора на внезапное расширение
в баке после прохождения жидкости
через отверстие.
Потери ho
практически равны потерям при истечении
через отверстие в газовую среду:
.
Следует
иметь в виду, что при истечении под
уровень вся кинетическая энергия струи,
приобретенная частицами жидкости в
отверстии, при попадании в покоящуюся
жидкость теряется на вихреобразование
так же, как при внезапном расширении.
Поэтому потери hв.р
численно равны соответствующему
скоростному напору, посчитанному по
средней скорости жидкости в струе с
учетом коэффициента Кориолиса
α:
.
Таким
образом, суммарные потери напора
.
Подставив
полученное выражение в уравнение
Бернулли, получим
.
Если
в этом уравнении за расчетный напор
принять выражение
,
то после преобразований можно получить
формулу, определяющую значение средней
скорости жидкости в сжатом сечении
струи:
,
которая
совпадает с формулой (4.2). Это значит,
что, проводя дальнейшие преобразования,
необходимые для получения формулы,
определяющей расход Q
при
истечении, можно получить формулы (4.
Внешним цилиндрическим насадком
называется
короткая трубка или сверление в толстой
стенке без обработки входной кромки
(рисунок 4.3). Его длина l
= (3…5)
d,
где
d
—
диаметр отверстия.
На практике при
истечении в газовую среду можно наблюдать
два режима истечения жидкости через
цилиндрический насадок: безотрывный
(см. рисунок 4.3, а)
и
с отрывом потока от стенок (см. рис. 4.3,
б).
Безотрывный
режим истечения характеризуется тем,
что внутри насадка поток жидкости
вначале сжимается до некоторого
минимального поперечного сечения,
площадь которого можно определить
по значению коэффициента сжатия струи
,
взятого для случая истечения жидкости
через отверстие в тонкой стенке, а затем
расширяется до размеров отверстия в
насадке. В итоге при таком режиме
истечения из насадка на его выходе
сжатие струи отсутствует (
= 1) и площадь сечения струи равна площади
проходного сечения отверстия в насадке.
Поэтому в данном случае при определении
расхода Q
по
формуле (4. 7) коэффициент расхода
7) коэффициент расхода
=
.
Для
этого случая при турбулентном режиме
течения жидкости внутри насадка (α = 1)
и коэффициенте потерь
=
0,5 (потери напора определяются как потери
при внезапном сужении) коэффициент
расхода
.
Сравнение
полученных коэффициентов скорости
и
расхода
со
значениями этих коэффициентов при
истечении жидкости через отверстие в
тонкой стенке (
= 0,97,
=
0,62) показывает, что при безотрывном
истечении через цилиндрический насадок
расход Q
получается
больше, чем при истечении через такое
же отверстие в тонкой стенке. Средняя
скорость
жидкости
в потоке на выходе из насадка при этом
получается меньше. Уменьшение скорости
вызвано большими потерями напора в
насадке по сравнению с потерями, которые
возникают на входной кромке отверстия
в тонкой стенке.
У
Рисунок
4.3 – Схемы истечения жидкости через
внешний цилиндрический насадок:
а
– безотрывный режим истечения; б – с
отрывом потока от стенок
величение
расхода Q
при
этом является следствием отсутствия
сжатия струи на выходе из насадка. Кроме
Кроме
того, при безотрывном истечении на входе
в насадок поток сжимается, а значит, в
соответствии с законом Бернулли скорость
движения жидкости увеличивается, а
давление в этом месте уменьшается по
сравнению с давлением среды, куда
происходит истечение. Причем степень
сжатия потока, а следовательно, и степень
уменьшения давления в узком сечении
потока тем больше, чем больше расчетный
напор Hр.
При этом на входной кромке отверстия
создается больший перепад давления,
чем при истечении жидкости через
отверстие в тонкой стенке при одном и
том же Hр.
В результате этого обеспечиваются
дополнительный приток жидкости из бака
в насадок и увеличение расхода Q.
Со сжатием потока на входе в насадок,
а также с зависимостью степени сжатия
от расчетного напора Нр
связано
внезапное изменение режима истечения
через насадок. Это происходит при
определенном критическом расчетном
напоре Hкр,
который при истечении воды в атмосферу
составляет около 14 м водяного столба.
Внешне эта смена режима истечения
заключается в том, что поток жидкости
отрывается от стенок насадка и жидкость
истекает в атмосферу, не касаясь их.
Этот режим истечения получил название
истечение с отрывом потока от стенок
насадка (см. рисунок 4.3, б).
При
истечении до отрыва потока от стенок
давление в узком сечении потока
приближается к давлению насыщенных
паров. Как известно, в потоке при таком
давлении следует ожидать возникновения
кавитации. Однако кавитационный режим
течения при истечении в газовую среду
не успевает сформироваться. Возникающая
начальная стадия кавитации способствует
проникновению газовой среды внутрь
насадка. Начиная с этого момента струя
жидкости после сжатия теряет взаимодействие
со стенками насадка и уже не расширяется,
а перемещается внутри насадка, не
соприкасаясь с его стенками. Истечение
становится таким же, как и при истечении
через отверстие в тонкой стенке (см.
подраздел 4.1), с теми же значениями
коэффициентов
,
и
.
Таким образом, при смене режима истечения
происходит скачкообразное уменьшение
расхода приблизительно на 20 % за счет
существенного сокращения площади
сечения потока.
Следует также
отметить, что если после отрыва потока
от стенок напор Hр
начать снижать, то режим истечения с
отрывом сохраняется вплоть до самых
малых значений напора, пока не произойдет
самопроизвольное смачивание внутренней
поверхности насадка. Это значит, что
режим истечения с отрывом через
цилиндрический насадок возможен и при
Hр
< Hкр.
Следовательно, при Hр
< Hкр
возможны оба режима истечения.
Если
жидкость истекает через цилиндрический
насадок под уровень, то отрыва потока
от стенок не происходит. Начиная с
момента, когда в узком сечении потока
внутри насадка давление становится
близким к давлению насыщенных паров
жидкости, на входе в насадок возникает
кавитация и происходит связанное с ней
увеличение сопротивления насадка.
Итак,
использование внешнего цилиндрического
насадка вместо отверстия в тонкой стенке
обеспечивает в режиме безотрывного
истечения при тех же значениях расчетного
напора и поперечных размеров отверстия
увеличение расхода через насадок.
Однако
внешний цилиндрический насадок имеет
и недостатки:
— в режиме безотрывного
истечения — большое сопротивление и
недостаточно высокий коэффициент
расхода;
— в режиме истечения с
отрывом — низкий коэффициент расхода;
—
двойственность режима истечения в
газовую среду при Hр
< Hкр;
—
возможность возникновения кавитации
при истечении под уровень.
Это
необходимо учитывать при использовании
цилиндрического насадка в качестве
жиклера, дросселя или форсунки. Улучшить
внешний цилиндрический насадок можно
за счет скругления входной кромки
насадка. Для жиклеров рекомендуется
снятие фаски на входе в отверстие с
углом конусности около 60°.
Чем больше
радиус закругления входной кромки
насадка, тем ниже его коэффициент
сопротивления и тем выше коэффициент
расхода. В пределе при радиусе кривизны,
равном толщине стенки, цилиндрический
насадок приближается к коноидальному
насадку, или соплу.
Рисунок
4.4 – Примеры улучшенных насадков:
а
– коноидальный насадок, или сопло; б –
диффузорный насадок
^
Коноидалъный насадок (сопло) (рисунок
4.
4.4 Истечение жидкости через проходные
сечения в гидравлических устройствах
При
определении расхода Q
через
проходные сечения, образованные
взаимным расположением деталей в
гидравлических устройствах, кроме
оценки коэффициента расхода
необходимо,
как правило, определять площадь S
проходного
сечения отверстия в функции смещения
х
одной
из деталей относительно другой. Обычно
величина х
и
определяет степень открытия проходного
сечения.
Для расчетов рекомендуется
использовать формулу
,
где
S(x)
— расчетная
площадь проходного сечения, определяемая
по значению смещения х
перекрывающей
детали;—
перепад
давления на проходном сечении.
— Истечение жидкости через отверстие
4 ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
4.1 Истечение через отверстие в тонкой стенке
Рассмотрим истечение жидкости через отверстие диаметром d0 в стенке бака, расположенное на глубине Н0, в газовую среду с некоторым давлением р1 (рисунок 4.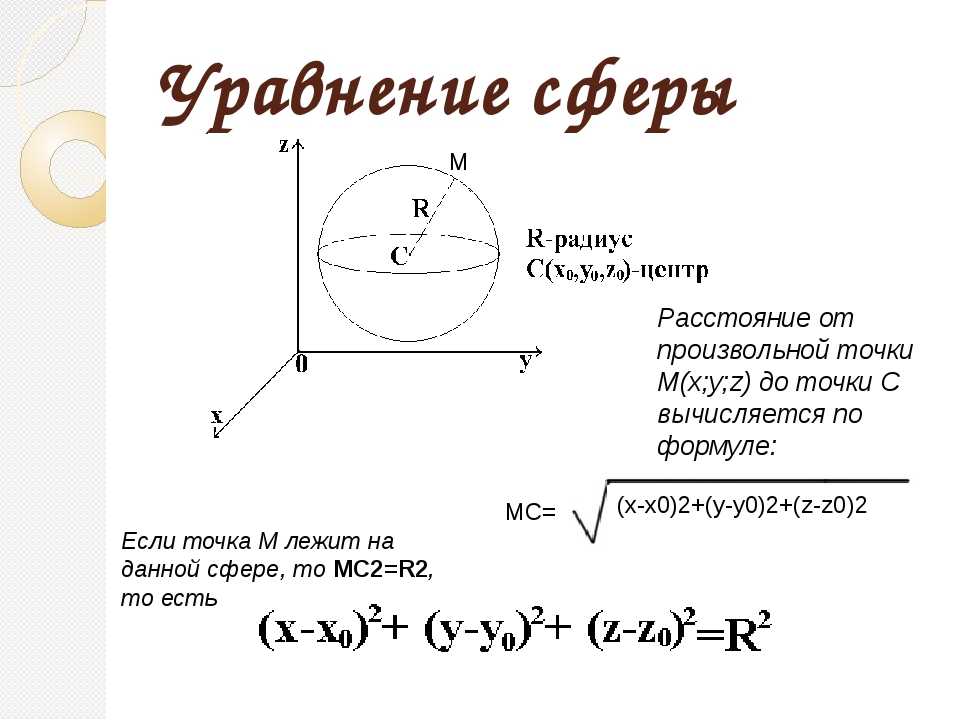 1, a). При этом предполагается, что если отверстие мало по сравнению с размерами бака и глубиной Н0, то другие стенки бака и свободная поверхность жидкости не влияют на приток жидкости к отверстию.
1, a). При этом предполагается, что если отверстие мало по сравнению с размерами бака и глубиной Н0, то другие стенки бака и свободная поверхность жидкости не влияют на приток жидкости к отверстию.
Характер истечения в этом случае показан на рисунке 4.1, б. Частицы жидкости приближаются к отверстию из всего близлежащего объема, двигаясь по различным траекториям. Некоторые из них при попадании в отверстие должны изменить направление своего движения на 90°. Так как каждая частица имеет массу, то мгновенно изменить направление своего движения она не может. Следствием этого является сжатие струи жидкости при истечении. Процесс сжатия струи практически завершается на расстоянии, равном примерно одному диаметру отверстия, и после этого струя приобретает цилиндрическую форму с диаметром поперечного сечения dc. Точно такими же будут условия истечения, если отверстие выполнено в толстой стенке со снятием фаски с внешней стороны.
Степень сжатия струи оценивается коэффициентом сжатия ε, равным отношению площади поперечного сечения струи к площади отверстия
. (4.1)
(4.1)
Определим расход Q жидкости через рассматриваемое отверстие. Для этого запишем уравнение Бернулли для двух сечений (см. рисунок 4.1, а): сечения 0-0 и сечения 1-1. Сечение 0-0 — это открытая поверхность жидкости в баке, следовательно, в нем давление р0, а скорость жидкости можно считать равной нулю. Сечение 1-1 струи должно быть выбрано в той ее части, где струя уже приняла цилиндрическую форму; тогда в этом сечении давление равно давлению р1 окружающей среды. Если в качестве плоскости сравнения выбрать горизонтальную плоскость, проходящую через ось отверстия, то получим
,
где α — коэффициент Кориолиса, учитывающий неравномерность распределения скорости по сечению 1—1 струи;
— средняя скорость жидкости в сечении 1—1;
— коэффициент сопротивления отверстия, учитывающий торможение частиц жидкости о входную кромку отверстия.
Перенесем первое слагаемое правой части уравнения в левую часть и обозначим ее как расчетный напор , тогда
;
отсюда средняя скорость истечения жидкости
, (4.2)
где — безразмерная величина, получившая название коэффициент скорости и определяемая по формуле
. (4.3)
В случае истечения идеальной жидкости (α = 1 и = 0) из формулы (4.3) следует, что = 1, т.е. скорость истечения идеальной жидкости
. (4.4)
Таким образом, на основании сравнения формул (4.3) и (4.4) можно сформулировать физический смысл коэффициента скорости . Это величина, равная отношению средней скорости истечения реальной жидкости к скорости истечения идеальной жидкости в тех же условиях. Очевидно, что при истечении реальной жидкости коэффициент всегда меньше единицы.
Расход Q при истечении определим как произведение средней скорости истечения реальной жидкости и фактической площади живого сечения струи. Используя формулы (4.1) и (4.3), получим
.
Произведение двух безразмерных коэффициентов и принято называть коэффициентом расхода и обозначать
. (4.5)
Тогда
. (4.6)
Из (4.6) следует, что
Таким образом, физический смысл коэффициента расхода состоит в том, что он численно равен отношению действительного расхода Q при истечении жидкости к тому расходу Qu, который имел бы место при отсутствии сжатия струи и сопротивления истечению.
Следует обратить внимание на то, что Qu не является расходом при истечении идеальной жидкости, так как идеальная жидкость отличается от реальной только отсутствием вязкости. Эффект же сжатия струи при истечении идеальной жидкости, связанный с инерционными свойствами частиц жидкости, в условиях отсутствия трения проявляется в еще большей степени.
Эффект же сжатия струи при истечении идеальной жидкости, связанный с инерционными свойствами частиц жидкости, в условиях отсутствия трения проявляется в еще большей степени.
На практике формула (4.6) используется достаточно редко из-за сложностей, возникающих при определении расчетного напора Hр, особенно в закрытых гидросистемах. Поэтому сделаем следующие преобразования. Обозначим внутри бака на уровне оси отверстия на некотором удалении от него (где скорость жидкости можно принять равной нулю) давление (см. рисунок 4.1, а), тогда перепад давления Δр, под действием которого происходит истечение жидкости через отверстие, запишется в виде
.
Выразив из этой формулы напор Hp и подставив его в формулу (4.6), получим
. (4.7)
При помощи формулы (6.7) решается основная задача — определение расхода жидкости при истечении. Она широко применяется при расчетах элементов машиностроительных гидросистем.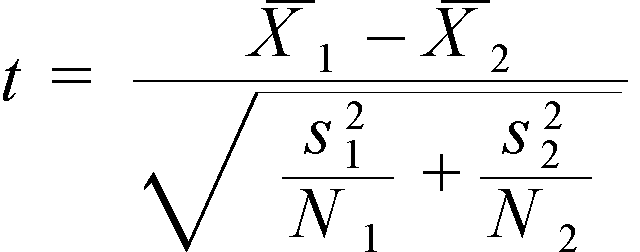
Таким образом, нами введены в рассмотрение три коэффициента — , и , характеризующие процесс истечения жидкости. Все они являются функцией числа Рейнольдса Re. Однако для маловязких жидкостей (воды, бензина и др.), истечение которых, как правило, происходит при больших значениях Re, эти коэффициенты практически постоянны: = 0,64; = 0,97; = 0,62. При истечении минеральных масел через круглые отверстия в области квадратичного сопротивления можно принять = 0,65.
4.2 Истечение под уровень
При течении жидкости в закрытых руслах часто приходится иметь дело с истечением жидкости не в газовую среду, а в пространство, заполненное этой же жидкостью (рисунок 4.2). Такое истечение называется истечением под уровень или истечением через затопленное отверстие.
Здесь, так же как и в предыдущем случае, при определении расхода Q следует составить уравнение Бернулли. Запишем его для сечений 1-1 и 2-2, в которых скорости движения жидкости принимаются равными нулю:
,
где — потери напора при движении жидкости между сечениями 1-1 и 2-2.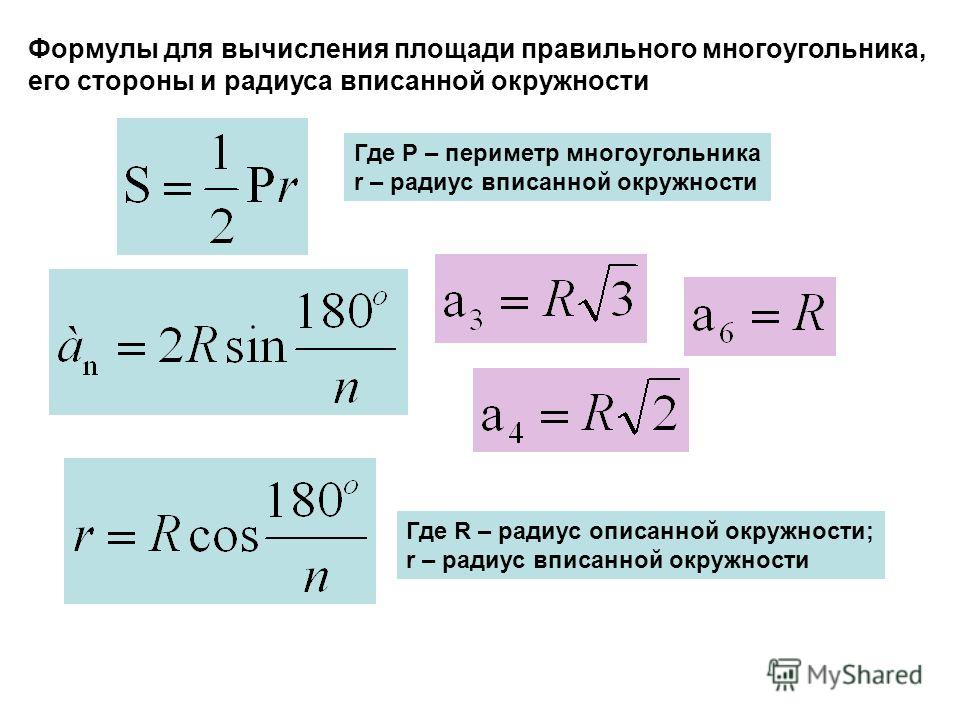
При определении потерь напора в этом случае необходимо учитывать, что они складываются из двух составляющих:
,
где ho — потери напора на торможение частиц жидкости о входную кромку отверстия;
hв.р — потери напора на внезапное расширение в баке после прохождения жидкости через отверстие.
Потери ho практически равны потерям при истечении через отверстие в газовую среду:
.
Следует иметь в виду, что при истечении под уровень вся кинетическая энергия струи, приобретенная частицами жидкости в отверстии, при попадании в покоящуюся жидкость теряется на вихреобразование так же, как при внезапном расширении. Поэтому потери hв.р численно равны соответствующему скоростному напору, посчитанному по средней скорости жидкости в струе с учетом коэффициента Кориолиса α:
.
Таким образом, суммарные потери напора
.
Подставив полученное выражение в уравнение Бернулли, получим
.
Если в этом уравнении за расчетный напор принять выражение , то после преобразований можно получить формулу, определяющую значение средней скорости жидкости в сжатом сечении струи:
,
которая совпадает с формулой (4.2). Это значит, что, проводя дальнейшие преобразования, необходимые для получения формулы, определяющей расход Q при истечении, можно получить формулы (4.6) и (4.7).
Таким образом, как при истечении в газовую среду, так и при истечении под уровень расчетные формулы, определяющие расход Q, имеют один и тот же вид. Кроме того, как показала практика, коэффициенты , и , использующиеся в этих формулах, в обоих случаях истечения имеют одинаковые значения при равенстве соответствующих чисел Рейнольдса.
4.3 Истечение через насадки
Анализ полученных формул (4.6) и (4.7) позволяет заключить, что увеличение расхода Q при истечении через отверстие с неизменными So и Hр, возможно при увеличении коэффициента расхода . Решению этой задачи служат насадки различной конструкции. Различают следующие типы насадков: цилиндрические (внешний и внутренний), конические (сходящийся и расходящийся), коноидальные и комбинированные.
Решению этой задачи служат насадки различной конструкции. Различают следующие типы насадков: цилиндрические (внешний и внутренний), конические (сходящийся и расходящийся), коноидальные и комбинированные.
Внешним цилиндрическим насадком называется короткая трубка или сверление в толстой стенке без обработки входной кромки (рисунок 4.3). Его длина l = (3…5) d, где d — диаметр отверстия.
На практике при истечении в газовую среду можно наблюдать два режима истечения жидкости через цилиндрический насадок: безотрывный (см. рисунок 4.3, а) и с отрывом потока от стенок (см. рис. 4.3, б).
Безотрывный режим истечения характеризуется тем, что внутри насадка поток жидкости вначале сжимается до некоторого минимального поперечного сечения, площадь которого можно определить по значению коэффициента сжатия струи , взятого для случая истечения жидкости через отверстие в тонкой стенке, а затем расширяется до размеров отверстия в насадке. В итоге при таком режиме истечения из насадка на его выходе сжатие струи отсутствует ( = 1) и площадь сечения струи равна площади проходного сечения отверстия в насадке. Поэтому в данном случае при определении расхода Q по формуле (4.7) коэффициент расхода = .
В итоге при таком режиме истечения из насадка на его выходе сжатие струи отсутствует ( = 1) и площадь сечения струи равна площади проходного сечения отверстия в насадке. Поэтому в данном случае при определении расхода Q по формуле (4.7) коэффициент расхода = .
Для этого случая при турбулентном режиме течения жидкости внутри насадка (α = 1) и коэффициенте потерь = 0,5 (потери напора определяются как потери при внезапном сужении) коэффициент расхода
.
Сравнение полученных коэффициентов скорости и расхода со значениями этих коэффициентов при истечении жидкости через отверстие в тонкой стенке ( = 0,97, = 0,62) показывает, что при безотрывном истечении через цилиндрический насадок расход Q получается больше, чем при истечении через такое же отверстие в тонкой стенке. Средняя скорость жидкости в потоке на выходе из насадка при этом получается меньше. Уменьшение скорости вызвано большими потерями напора в насадке по сравнению с потерями, которые возникают на входной кромке отверстия в тонкой стенке.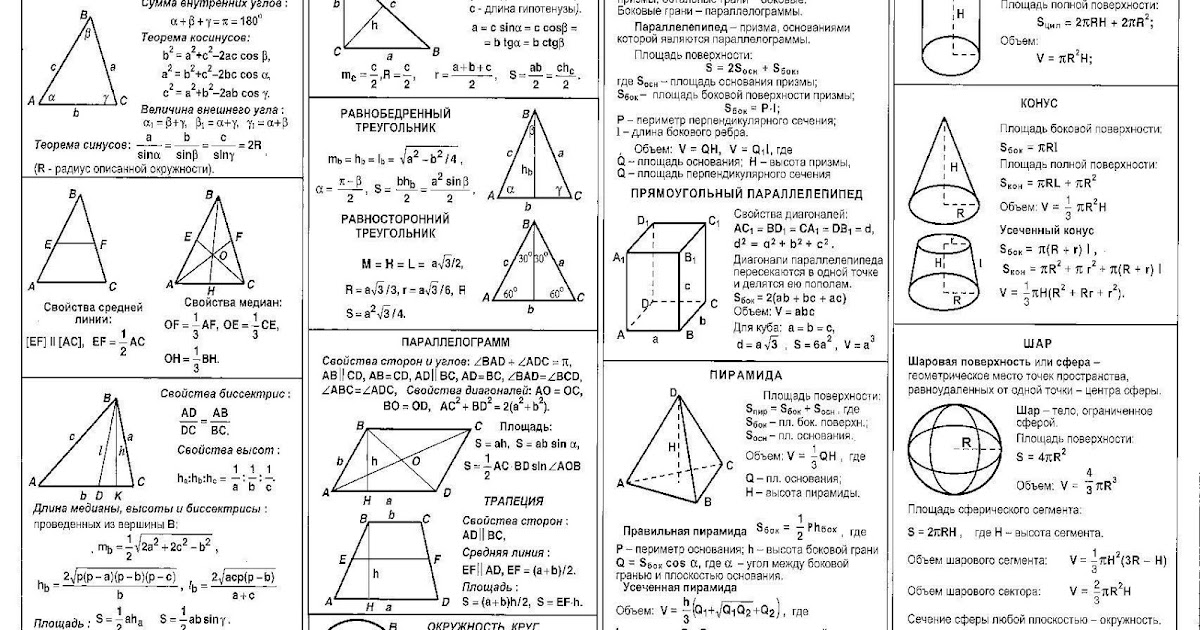
Увеличение расхода Q при этом является следствием отсутствия сжатия струи на выходе из насадка. Кроме того, при безотрывном истечении на входе в насадок поток сжимается, а значит, в соответствии с законом Бернулли скорость движения жидкости увеличивается, а давление в этом месте уменьшается по сравнению с давлением среды, куда происходит истечение. Причем степень сжатия потока, а следовательно, и степень уменьшения давления в узком сечении потока тем больше, чем больше расчетный напор Hр. При этом на входной кромке отверстия создается больший перепад давления, чем при истечении жидкости через отверстие в тонкой стенке при одном и том же Hр. В результате этого обеспечиваются дополнительный приток жидкости из бака в насадок и увеличение расхода Q.
Со сжатием потока на входе в насадок, а также с зависимостью степени сжатия от расчетного напора Нрсвязано внезапное изменение режима истечения через насадок. Это происходит при определенном критическом расчетном напоре Hкр, который при истечении воды в атмосферу составляет около 14 м водяного столба. Внешне эта смена режима истечения заключается в том, что поток жидкости отрывается от стенок насадка и жидкость истекает в атмосферу, не касаясь их. Этот режим истечения получил название истечение с отрывом потока от стенок насадка (см. рисунок 4.3, б).
Это происходит при определенном критическом расчетном напоре Hкр, который при истечении воды в атмосферу составляет около 14 м водяного столба. Внешне эта смена режима истечения заключается в том, что поток жидкости отрывается от стенок насадка и жидкость истекает в атмосферу, не касаясь их. Этот режим истечения получил название истечение с отрывом потока от стенок насадка (см. рисунок 4.3, б).
При истечении до отрыва потока от стенок давление в узком сечении потока приближается к давлению насыщенных паров. Как известно, в потоке при таком давлении следует ожидать возникновения кавитации. Однако кавитационный режим течения при истечении в газовую среду не успевает сформироваться. Возникающая начальная стадия кавитации способствует проникновению газовой среды внутрь насадка. Начиная с этого момента струя жидкости после сжатия теряет взаимодействие со стенками насадка и уже не расширяется, а перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится таким же, как и при истечении через отверстие в тонкой стенке (см. подраздел 4.1), с теми же значениями коэффициентов , и . Таким образом, при смене режима истечения происходит скачкообразное уменьшение расхода приблизительно на 20 % за счет существенного сокращения площади сечения потока.
Истечение становится таким же, как и при истечении через отверстие в тонкой стенке (см. подраздел 4.1), с теми же значениями коэффициентов , и . Таким образом, при смене режима истечения происходит скачкообразное уменьшение расхода приблизительно на 20 % за счет существенного сокращения площади сечения потока.
Следует также отметить, что если после отрыва потока от стенок напор Hр начать снижать, то режим истечения с отрывом сохраняется вплоть до самых малых значений напора, пока не произойдет самопроизвольное смачивание внутренней поверхности насадка. Это значит, что режим истечения с отрывом через цилиндрический насадок возможен и при Hр < Hкр. Следовательно, при Hр < Hкр возможны оба режима истечения.
Если жидкость истекает через цилиндрический насадок под уровень, то отрыва потока от стенок не происходит. Начиная с момента, когда в узком сечении потока внутри насадка давление становится близким к давлению насыщенных паров жидкости, на входе в насадок возникает кавитация и происходит связанное с ней увеличение сопротивления насадка.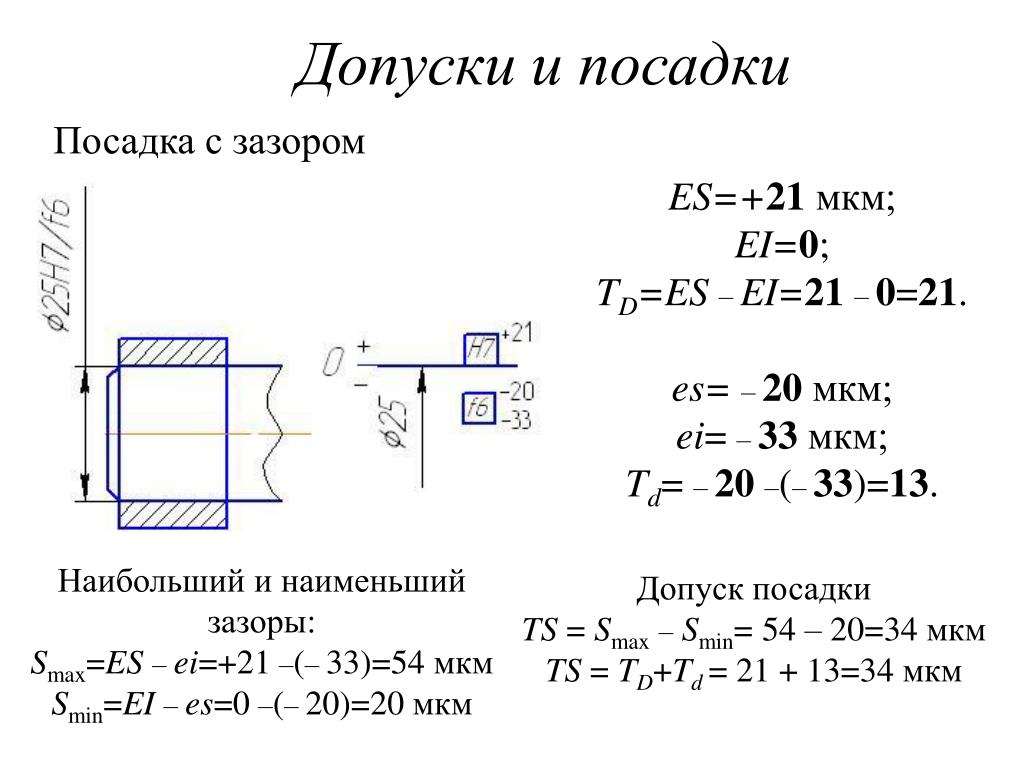
Итак, использование внешнего цилиндрического насадка вместо отверстия в тонкой стенке обеспечивает в режиме безотрывного истечения при тех же значениях расчетного напора и поперечных размеров отверстия увеличение расхода через насадок.
Однако внешний цилиндрический насадок имеет и недостатки:
— в режиме безотрывного истечения — большое сопротивление и недостаточно высокий коэффициент расхода;
— в режиме истечения с отрывом — низкий коэффициент расхода;
— двойственность режима истечения в газовую среду при Hр < Hкр;
— возможность возникновения кавитации при истечении под уровень.
Это необходимо учитывать при использовании цилиндрического насадка в качестве жиклера, дросселя или форсунки. Улучшить внешний цилиндрический насадок можно за счет скругления входной кромки насадка. Для жиклеров рекомендуется снятие фаски на входе в отверстие с углом конусности около 60°.
Чем больше радиус закругления входной кромки насадка, тем ниже его коэффициент сопротивления и тем выше коэффициент расхода.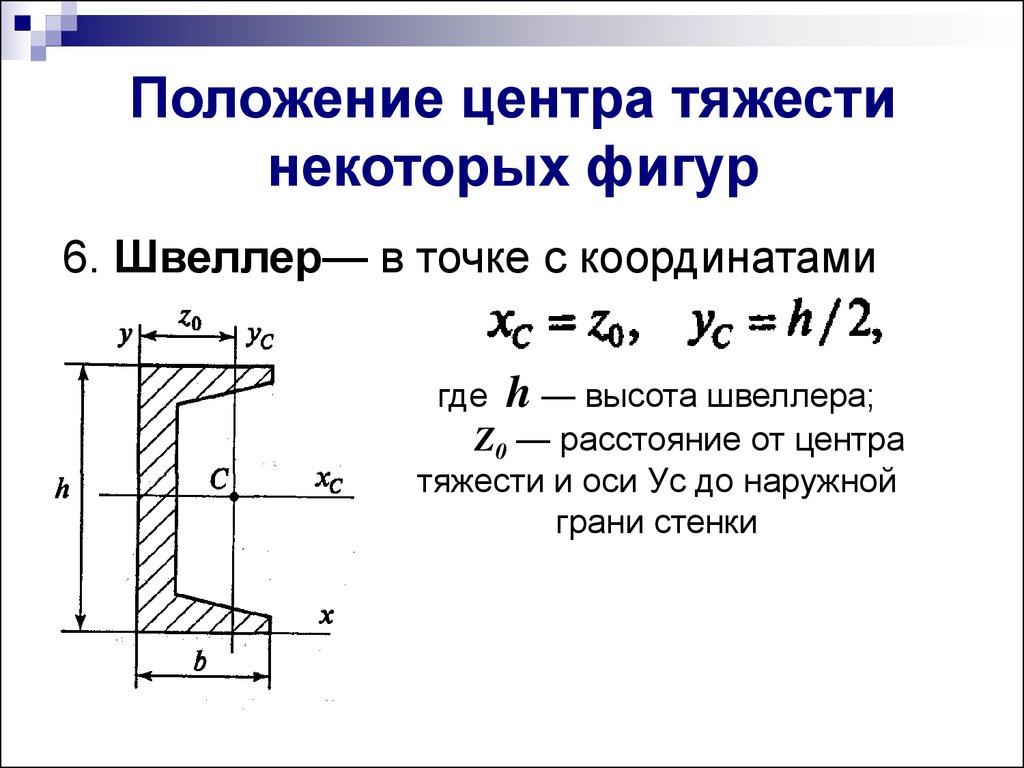 В пределе при радиусе кривизны, равном толщине стенки, цилиндрический насадок приближается к коноидальному насадку, или соплу.
В пределе при радиусе кривизны, равном толщине стенки, цилиндрический насадок приближается к коноидальному насадку, или соплу.
Коноидалъный насадок (сопло) (рисунок 4.4, а) очерчивается по форме естественно сжимающейся струи, поэтому поток жидкости на выходе насадка получается безотрывным, параллельно-струйным и устойчивым к возникновению кавитации. Для этого насадка коэффициент сжатия струи = 1, а коэффициент = = 0,96…0,99.
Диффузорный насадок (рисунок 4.4, б) представляет собой комбинацию сопла и диффузора. Установка диффузора с оптимальным углом на выходе позволяет, не меняя проходного сечения отверстия (сечение 1-1) и расчетного напора, повысить расход жидкости почти в 2,5 раза по сравнению с расходом через сопло. Недостатком диффузорного насадка является склонность его к возникновению кавитации в узком сечении 1-1.
4.4 Истечение жидкости через проходные сечения в гидравлических устройствах
При определении расхода Q через проходные сечения, образованные взаимным расположением деталей в гидравлических устройствах, кроме оценки коэффициента расхода необходимо, как правило, определять площадь S проходного сечения отверстия в функции смещения х одной из деталей относительно другой. Обычно величина х и определяет степень открытия проходного сечения.
Обычно величина х и определяет степень открытия проходного сечения.
Для расчетов рекомендуется использовать формулу
,
где S(x) — расчетная площадь проходного сечения, определяемая по значению смещения х перекрывающей детали; — перепад давления на проходном сечении.
Таблица 4.1 — Основные величины, характеризующие истечения
В таблице 4.1 и на рисунке 4.5 приведены основные варианты расчетных схем, полученные в результате анализа наиболее часто встречающихся случаев при решении задач определения расхода. В основном эти варианты отличаются формой детали, перекрывающей круглое проходное сечение диаметром d, и соотношением поперечных размеров отверстия и перекрывающей детали. Для каждого из них даются рекомендуемые значения коэффициента расхода в области квадратичного сопротивления и формула, позволяющая оценить площадь S(x) соответствующего проходного сечения.
11-я лекция
12-я лекция, 2010
8. ИСТЕЧЕНИЕ ЖИДКОСТИ
ИСТЕЧЕНИЕ ЖИДКОСТИ
ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
8.1 Истечение через отверстия в тонкой стенке и насадки (короткие трубки)
при постоянном напоре.
8.2. Истечение при совершенном сжатии.
8.3 Скорость истечения при совершенном сжатии. Коэффициенты:ε, ξ, φ, μ
8.4 Истечение при несовершенном сжатии
8.5. Истечение под уровень
8.6. Истечение через насадки при постоянном напоре.
8.7 Первый режим течения.
8.8 Второй режим истечения
8.1. Истечение через
отверстия и насадки (короткие трубки)
при постоянном напоре.
Рассматривается
процесс истечение жидкости из резервуаров через отверстия и насадки в атмосферу
и в пространство, заполненное жидкостью.
При истечении запас
потенциальной энергии жидкости в
резервуаре, переходит в кинетическую энергию свободной струи, при переходе есть
потери энергии на трение и завихрение
частиц жидкости.
Задачей изучения
процесса истечения является определение скорости истечения и расхода жидкости.
Истечение
производится из резервуара с жидкостью под давлением Р0 на
свободной поверхности через круглое отверстие в тонкой стенке на глубине (во
много раз большей диаметра отверстия) Н0 >> dот (рис. 12.1).
Через отверстие
жидкость вытекает в воздушное пространство с давлением Р1.
Отверстие в стенке
имеет острую кромку. Частицы жидкости приближаются к отверстию из всего
прилежащего объема, двигаясь ускоренно по различным плавным траекториям (см.
рис.12.1б). Струя отрывается от стенки у кромки отверстия и затем сжимается. Формирование
сжатого сечения струи происходит на расстоянии
примерно одного диаметра отверстия.
Сжатие струи происходит
при плавном переходе от различных направлений движения жидкости в резервуаре.
12. 2. Истечение при
2. Истечение при
совершенном сжатии.
Совершенным сжатием называется наибольшее
сжатие струи, когда диаметр отверстия во
много раз меньше напора Н0.
Н0 >> dот
В этом случае боковые
стенки и свободная поверхность жидкости не влияют на поток жидкости к отверстию.
Сжатие струи оценивается
коэффициентом сжатия ε, равным отношению площади
поперечного сечения струи к площади отверстия
ε = Sc/S0 = (dc/d0)2. (12.1)
Для определения
скорости истечения и расхода из отверстия запишем уравнение Бернулли для движения
жидкости от свободной поверхности «0 – 0» в резервуаре и сечением
струи «1 – 1» (на рис.12.1а).
В рассматриваемом
случае уравнение Бернулли записывается для установившейся скорости, истечение происходит под постоянным напором,
над свободной поверхностью «0 – 0» давление
равно Р0, скорость
также равна нулю.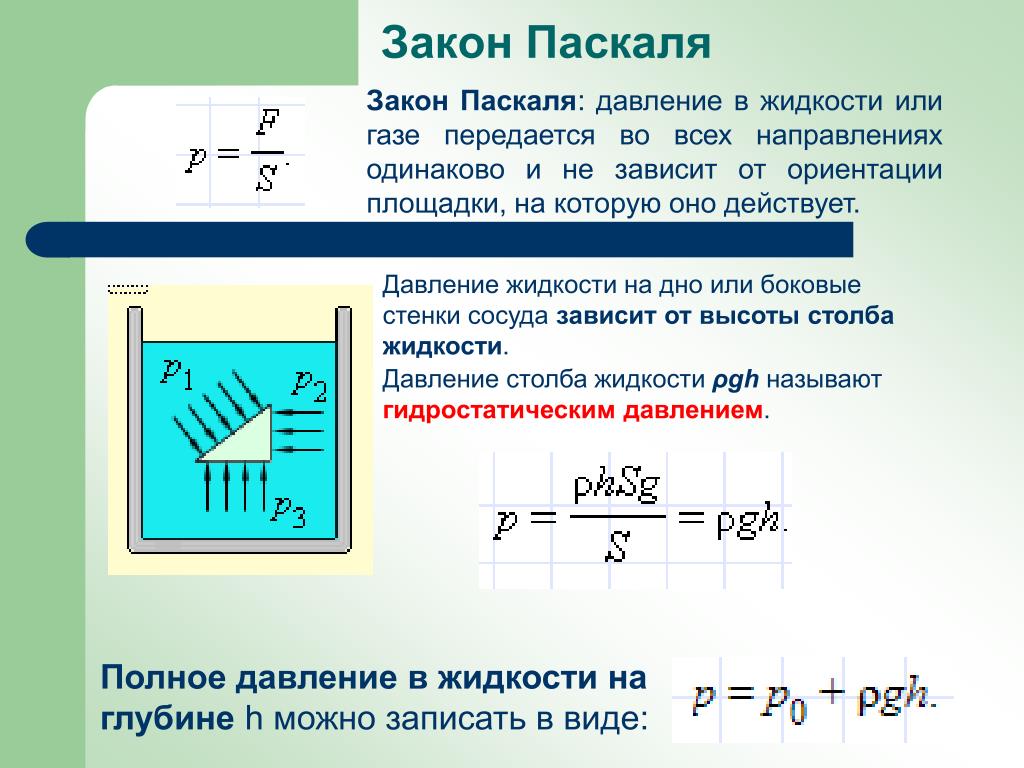
В сечении «1 – 1», струя примет цилиндрическую форму, давление Р1, скорость V1 предстоит определить из уравнения Бернулли для
потока реальной жидкости.
где ξ—
коэффициент, характеризующий сопротивление отверстия, -коэффициент Кориолиса из уравнения Бернулли
для потока вязкой жидкости, характеризующий неравномерность распределения
скоростей в потоке.
Если умножить
числитель и знаменатель выражения для α на ρ/2, можно убедиться, что α
является отношением действительной кинетической энергии потока в данном сечении
к кинетической энергии этого потока в этом сечения при равномерном распределении скоростей.
Выделив сумму
геометрического и пьезометрического напора Н = Н0 + (Р0 — Р1)/(ρg), получаем выражение,
связывающее скорость истечения и скоростной напор.
12.3 Скорость истечения
реальной жидкости при совершенном сжатии.
Коэффициенты:ε, ξ, φ, μ
Из выражения для
гидростатического напора, получим формулу для определения скорости истечения из
отверстия с острой кромкой для реальной жидкости
, (12.2)
где φ —
коэффициент скорости
. (12.3)
Для идеальной
жидкости, так как у нее отсутствует вязкость, трения и потерь на трение
нет ξ = 0, α = 1, следовательно,
φ
= 1.
Скорость
истечения идеальной жидкости из отверстия с острой кромкой
(12.4)
Из формулы (12.2) можно заключить, что коэффициент
скорости φ есть отношение скорости истечения реальной жидкости к скорости истечения
идеальной жидкости.
, (12.5)
Скорость
истечения реальной жидкости меньше идеальной
из-за вязкости и трения, поэтому коэффициент скорости φ всегда меньше единицы.
Измерения
показывают, что в средней части сечения струи эпюра скоростей является
равномерной, поэтому скорость в средней части струи близка к идеальной , наружный слой жидкости притормаживается при трении о края
стенки отверстия. Коэффициент φ
рассматривается, как коэффициент по средней скорости.
Умножив скорость истечения на площадь сечения струи, получим
выражение для расхода жидкости через отверстие с острой кромкой при совершенном
сжатии
. (12.6)
Коэффициентом
расхода μ называют произведение
значений коэффициентов сжатия ε и скорости
φ
μ = ε * φ.
Формула для
расхода через отверстие с острой кромкой с учетом выражения для μ
(12. 7) или
7) или
(12.8)
где ΔР
— расчетная разность давлений, под действием которой происходит истечение.
По этим формулам
определяется расход для всех случаев связанных с истечением из отверстия с острой кромкой и через насадки различных
форм.
Из уравнения (12.7)
следует, что
(12.9)
Коэффициент
расхода есть отношение действительного
расхода Q к расходу идеальной
жидкости Qи,
определенному по ее скорости . Действительный
расход всегда меньше расхода идеальной жидкости, следовательно, коэффициент
расхода всегда меньше единицы из-за сжатия струи и трения.
Коэффициенты
сжатия струи ε, сопротивления ξ, скорости φ, расхода μ = ε * φ зависят от
типа отверстия и насадка и от числа Рейнольдса.
На рис. 12.2
показаны составленные Альтшулем зависимости
для коэффициентов ε, φ и μ
для круглого отверстия в функции
числа Rеи, подсчитанного по
скорости истечения идеальной жидкости
Rеи=Vиd/ν = .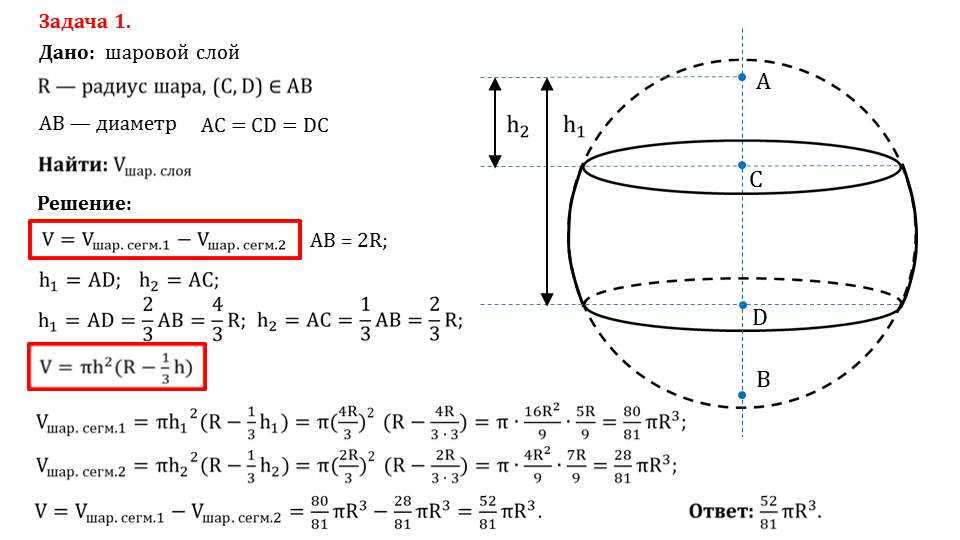
Увеличение числа Re означает
уменьшение сил вязкости, поэтому коэффициент φ возрастает в связи
с уменьшением коэффициента сопротивления ξ
(влияние трения становится меньше), коэффициент ε уменьшается из-за уменьшения торможения жидкости
у кромки отверстия и увеличения радиусов кривизны струи на входе в цилиндрическую
часть. При Rеи
→∞ значения коэффициентов приближаются к φ→1
и ε→0,6
и соответствуют истечению идеальной жидкости.
Коэффициент
расхода μ, определяемый
произведением ε на φ с увеличением Re сначала растет, что связано с сростом
φ,
а затем уменьшается в связи со
значительным падением ε
и при больших Rеи
равен μ = 0,60÷061.
В области малых Re (Rеи < 25) роль
вязкости велика, торможение жидкости у кромки значительно так, что сжатие струи отсутствует ε
= 1, φ = μ. В этом
В этом
случае можно пользоваться формулой:
(12.10)
12.3. Истечение при
несовершенном сжатии
Несовершенным
сжатием струи тогда, когда на формирование струи оказывает влияние близость боковых
стенок резервуара.
Боковые стенки успевают
направлять жидкость при подходе к отверстию, и струя сжимается в меньшей степени, чем при истечении
из резервуара неограниченных размеров при совершенном сжатии. Увеличивается коэффициент сжатия и коэффициент расхода.
При истечении из
цилиндрического резервуара через круглое отверстие, расположенное в центре торцевой
стенки при больших числах Re, коэффициент сжатия ε1можно
находить по формуле Жуковского для идеальной жидкости
ε1= 0,57 +0,043/(1,1 — n)
(12.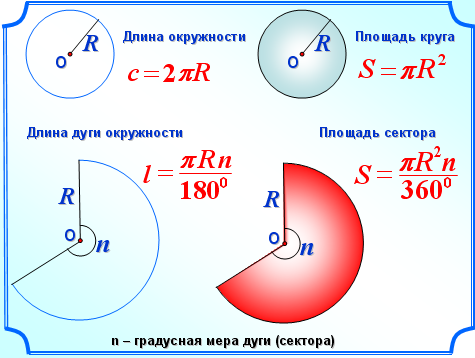 11)
11)
где n = S0/S1 отношение площади
отверстия S0 к
площади S1 поперечного
сечения резервуара.
Коэффициент
скорости φ при несовершенном сжатии мало зависит от отношения n и его
находят по графику на рис.12.2, коэффициент сопротивления отверстия ξ можно найти из формулы, связывающей
Коэффициент
расхода μ1 = ε1 φ
, уравнение Бернулли записывается для сечения «1-1» в резервуаре и сечения в
наиболее сжатой части струи, где давление равно Р0 –атмосферному.
Выразим V1 через V2 V1S1=V2 ε1S0;
V1=V2 ε1S0/S1;
V1=V2 ε1n
.
(12.12)
Откуда получаем:
скорость для несовершенного
сжатия струи
; (12. 13)
13)
расход для несовершенного
сжатия струи
(12.14)
12.5. Истечение под
уровень
Истечением под
уровень называется истечение жидкости в пространство, заполненное этой же жидкостью
(рис. 12.12).
Вся кинетическая
энергия струи теряется на вихреобразование, как при внезапном расширении.
Составляя уравнение
Бернулли относительно свободных поверхностей «0 – 0» и «2 –
2» скорости считаем равными нулю, а приравнивая к
первой и второй части члены уранения для сжатого сечения получим с учетом
коффициента α :
или
1-я сумма, 2-я сумма, 3- сжатое сечение
где Н – обозначен
расчетный напор, ξ – коэффициент сопротивления отверстия, имеющий примерно
то же значение, что и при истечении в атмосферу, V – скорость истечения в сжатом сечении
струи.
Скорость в этом
случае
(12.15)
Расход
, (12.16)
где Sc – площадь
сжатого сечения струи, S0
– площадь отверстия.
Получились такие же расчетные формулы, что и при истечении в
воздух, только расчетный напор Н в данном
случае представляет собой разность
гидростатических напоров по обе стороны стенки, т.е. скорость и расход
не зависят от высоты расположения
отверстия.
Коэффициенты
сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
12.6.
Истечение через насадки при постоянном напоре.
Внешним
цилиндрическим насадком называется короткая трубка длиной, равной l = (2÷6)d без
закругления входной кромки (рис.12.4а). Истечение через такой насадок в атмосферу может
происходить в двух режимах.
12.5.1.Первый режим течения- безотрывный:
струя после входа в насадок сжимается
примерно как при истечении через
отверстие в тонкой стенке.
Затем сжатая часть
струи расширяется до размеров отверстия, и из насадка выходит полным сечением. Такой
режим истечения называют безотрывным. На выходе диаметр струи равен диаметру отверстия.
Для маловязких
жидкостей средние значения коэффициентов
для этого режима при больших числах Re равны: μ=φ = 0,8, ξ = 0,5-0,63.
Коэффициент μ
расхода такого насадка при этом режиме истечения жидкости зависит от относительной
длины насадка l/d и числа Re. Однако и при достаточном значении
l/d не всегда возможен
этот режим.
Пусть
истечение жидкости происходит под действием давления Р0 в среду
газа с давлением Р2. Расчетный напор в этом случае
H = (P0 – Р2)/(ρg)
В
струе на выходе из насадка давление равно Р2, в суженном месте
струи внутри насадка, где скорость увеличена, давление Р1 меньше, чем
Р2.
Чем больше напор, под которым происходит истечение и расход через насадок, тем
меньше абсолютное давление Р1.
Разность давлений Р2 — Р1
растет пропорционально напору Н.
Покажем
это, составив уравнение Бернулли для сечений 1 — 1 и 2 – 2,α = 1 (см. рис.12.4а):
Последний
член уравнения представляет собой потерю напора на расширение потока, которое в
данном случае происходит примерно так же, как и при внезапном расширении трубы (формула
Борда). Сжатие струи внутри насадка можно оценить коэффициентом сжатия ε,
как и в случае отверстия, поэтому на основании уравнения расхода
ε=S1/S2; V1S1=V2S2;
V1/V2=S2/S1=1/ ε;
V1=V2/ε. (12.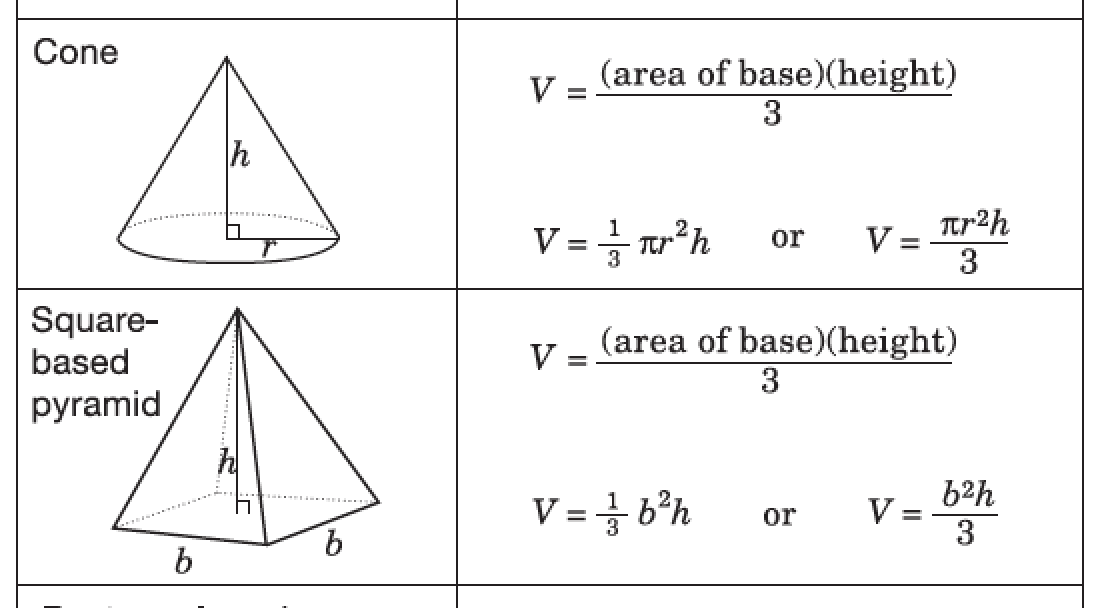 17)
17)
Заменив
с помощью этого соотношения скорость V1 в уравнении
Бернулли на скорость V2, а ее скорость V2 выражением через , найдем падение давления внутри насадка:
(12.18)
Подставляя сюда φ = 0,8 и
ε=0.63, получаем
(Р2 — Р1 ) ≈ 0,75ρgH (12.19)
Если
истечение происходит в среду, где Р2 равно постоянному ,
например, атмосферному давлению, увеличение
напора до критической величины Нкр приводит
к уменьшению Р1 — абсолютное давление в сжатом сечение «1 – 1» внутри насадка может уменьшиться до давления насыщенных паров. Поэтому существует
величина напора, называемая критическим
напором
Hкр ≈ Р2 /(0,75ρg). (12.20)
Следовательно,
при Н
> Hкр
давление Р1 должно
стать отрицательным, но отрицательных давлений в жидкости не бывает, поэтому
первый режим истечения при
Н
> Hкр
делается невозможным. При Н ≈ Hкр происходит внезапное
При Н ≈ Hкр происходит внезапное
изменение режима истечения, переход от первого режима ко второму (см. рис.12.4в).
12.5.2. Второй режим истечения
характеризуется тем, что струя после сжатия уже не расширяется, сохраня
цилиндрическую форму, и перемещается внутри насадка, не соприкасаясь с его
стенками. Течение становится таким же, как из отверстия в тонкой стенке, с теми
же значениями коэффициентов. Следовательно, при переходе от первого режима ко
второму скорость возрастает, расход
уменьшается, благодаря сжатию струи.
Если
через насадок происходит истечение воды в атмосферу, то
Hкр ≈ Ра /(0,75ρg) = 10,33/0,75 ≈ 14 м.
Когда
давление Рн.п.
насыщенных паров истекающей жидкости соизмеримо с давлением Р2
среды, в которую происходит истечение,
пренебречь величиной Рн.п. нельзя, в формуле (12.19) следует принять Р1
= Рн. п.
п.
Hкр = (Ра –Рн.п.)/(0,75ρg) (12.21)
Если
после перехода от первого режима истечения ко второму уменьшить напор Н,
то второй режим будет сохраняться вплоть до самых малых Н. Это значит, что второй
режим истечения возможен при любых напорах, следовательно, при Н < Нкр возможны оба
режима.
При
истечении через цилиндрический насадок под уровень первый режим истечения не
будет отличаться от описанного выше. Но когда абсолютное давление внутри
насадка благодаря увеличению Н падает до давления насыщенных
паров перехода ко второму режиму не происходит, а начинается кавитационный
режим, при котором расход перестает зависеть от противодавления Р2,
получается эффект стабилизации расхода. При этом чем меньше относительное противодавление
Р2/Р0
=Рвых/Рвх =, которое является критерием кавитации, тем шире
область кавитации внутри насадка и тем меньше коэффициент расхода μ.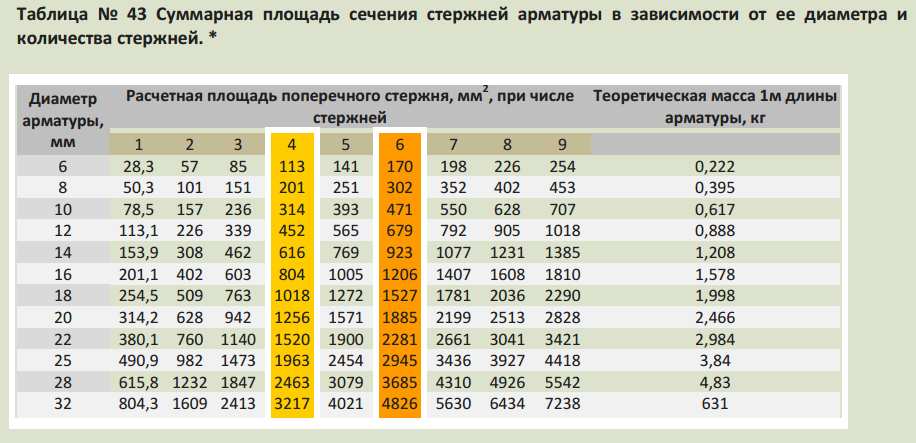
Таким
образом, при истечении жидкости через внешний цилиндрический насадок под
уровень коэффициент является функцией трех безразмерных критериев, а именно
μ = f (l/d, Re, ).
Результаты
новых экспериментальных исследований этого случаи истечения представлены в
безразмерных координатах на рис. 1.85. На рис.1.85а даны зависимости от Re при l/d = 3
для ряда значений , начиная от = 0 и до > , где — критическое
значение , соответствующее началу кавитации и, следовательно,
критерию ηкр(см. п. 1.23). На рис. 1.85б показаны области кавитационных и
безкавитационных режимов истечения через насадки с l/d = 3; 5 и 10. Увеличениепри возрастании Re объясняется уменьшением коэффициента ε сжатия струи
внутри насадка, т. е. увеличением степени сжатия, а уменьшение при увеличении l/d происходит из-за возрастания давления в сжатом сечении вследствие
е. увеличением степени сжатия, а уменьшение при увеличении l/d происходит из-за возрастания давления в сжатом сечении вследствие
увеличения потерь на трение по длине насадка.
Таким
образом, внешний цилиндрический насадок имеет существенные недостатки: на
первом режиме — большое сопротивление и недостаточно высокий коэффициент расхода,
а на втором — очень низкий коэффициент расхода. Недостатком является также двойст-венность
режима истечения в газовую среду при Н < Нкр, а следовательно двузначность
расхода при данном Н и возможность кавитации при истечении под уровень.
При
использовании цилиндрического насадка (сверления в толстой стенке), например в
качество жиклеров, дросселей или форсунок эти недостатки следует учитывать или
улучшать насадок.
Внешний
цилиндрический насадок может быть значительно улучшен путем закругления входной
кромки (см. штриховые линии на рис. 1.83) или устройства конического входа с
углом конусности около 60° (см.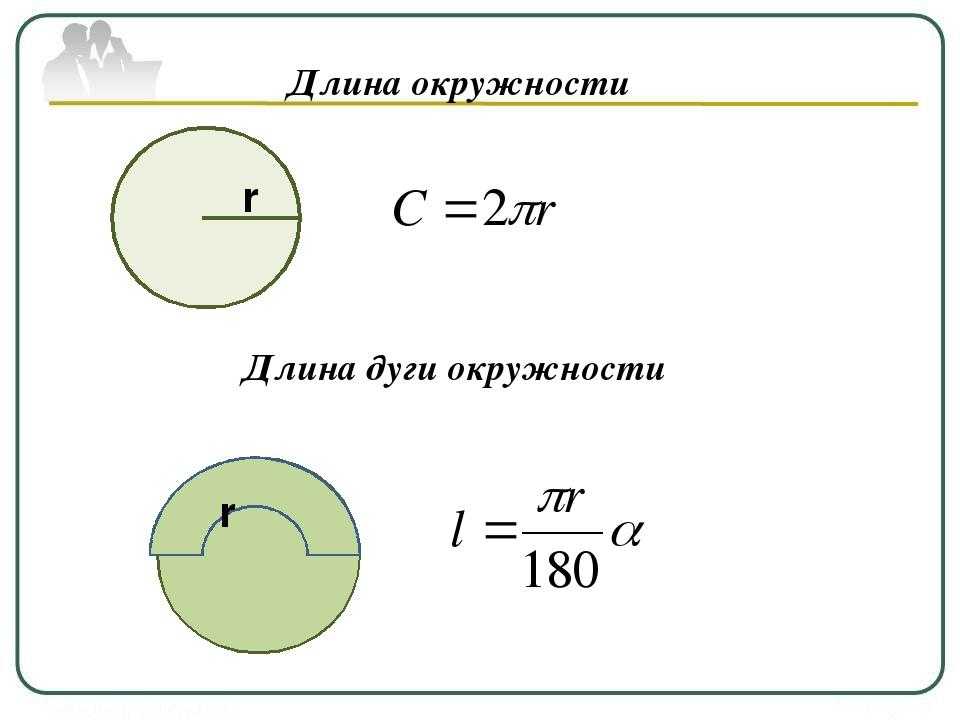 жиклер на рис. 1.75).
жиклер на рис. 1.75).
Чем
больше радиус закругления, тем выше коэффициент расхода и ниже коэффициент
сопротивления. В пределе при радиусе кривизны, равном толщине стенки, цилиндрический
насадок приближается к коноидальному насадку, или соплу.
Коноидальный
насадок (рис. 1.86) очерчивается приблизительно по форме естественно сжимающейся
струи и, благодаря этому, обеспечивает безотрывность течения внутри насадка в
параллельноструйность в выходном сечении. Это весьма распространеный насадок, так
как он имеет коэффициент расхода, близкий к единице, и очень малые потери
(коэффициент сжатия ε = 1), а также устойчивый режим течения без кавитации.
Значения
коэффициента сопротивления те же, что и при плавном сужении (см. п. 1.32), т.
е. ξ= 0,03 ÷ 0,1 (большим Re соответствуют малые ξ ‚ и наоборот). В соответствии с этим
μ =φ= 0,99÷0,96.
Диффузорный
насадок представляет собой комбинацию сопла и диффузора (рис. 1.87).
Приставка
диффузора к соплу влечет за собой снижение давления в узком месте насадка, а
следовательно, увеличение скорости и расхода жидкости через него. При том жедиаметре
При том жедиаметре
узкого сечения, что и у сопла, и том же напоре диффузорный насадок может дать
значительно больший расход (увеличение до 2,5 раза), чем сопло.
Такие насадки
применяют в том случае, когда заданы диаметр узкого сечения и напор и требуется
получить возможно больший расход. Однако, использовать диффузорных насадков
можно лишь при небольших напорах Н = 1 ÷4
м, так как иначе в узком месте насадка возникает кавитация. Следствием кавитации являются увеличение
сопротивления и уменьшение пропускной способности насадка.
На рис.1.88
показано падение коэффициента расхода диффузорного насадка с увеличением напора
вследствие кавитации, возникающей в узком месте насадка при истечении воды в атмосферу.
Коэффициент
расхода отнесен к площади узкого сечения, т. е. . Приведенная кривая получена в результате испытания диффузорного
насадка, обладающего наивыгоднейшим углом и степенью расширения, которые
обеспечивают наибольший коэффициент расхода.
Внутренний
цилиндрический насадок или насадок Борда, изображен на рис. 1.89. Там же
1.89. Там же
схематически показаны два режима истечения , аналогичные режимам истечения
через внешний цилиндрический насадок. Очертания струи при первом режиме
показаны сплошными линиями, а при втором – штриховыми. Так как частицы жидкости
приближаются к входному отверстию
насадка из всего прилежащего объема, а некоторые из них, попадающие на
периферию струи, изменяют направление своего движения на 180°, то степень
сжатия струи в данном насадке больше, а коэффициент ε меньше, чем во внешнем
цилиндрическом насадке. Значение ε в этом случае при истечении идеальной
жидкости может быть получено на основании
теоремы Эйлера об изменения количества движения (см. п. 1.15). Применим эту
теорему к фиксированному объему в виде кругового цилиндра ABCD соосного с насадком, и с основанием
CD, достаточно удаленным от насадка, где V=0. Пренебрегая толщиной стенки
насадка на основании указанной теоремы при втором режиме истечения получим
PS0 = ρSс*V2,
где
P— давление в центре
основания CD, S0и Sс —
площади отверстия насадка и сечения струи (силы давления жидкости на кольцевые
площади оснований цилиндра ABCD уравновешиваются, а избыточное
давление по площади S0в
плоскости АВ равно нулю.
С
другой стороны, для скорости истечения имеем
1 .
IIосле
подстановки второго уравнения в первое и сокращения на Р и ρ получим
ε = Sс / S0 = ½.
Этому
значению ε соответствуют значения коэффициентов расхода μ = 0,71 и потерь
ξ =1, что подтверждается опытами при первом режиме истечения и больших
числах Рейнольдса.
Истечение жидкости через малые отверстия и насадки при постоянном напоре
На практике часто приходится встречаться с истечением жидкости через различные отверстия и насадки. При этом характер истечения существенно зависит от условий истечения.
Задача об истечении сводится к определению скорости истечения и расхода вытекающей жидкости. Наиболее просто и точно эта задача решается в случае, когда напор одинаков по всему поперечному сечению отверстия. Это условие выполняется при истечении жидкости из малых отверстий.
«Малым отверстием» называется такое отверстие, линейный размер которого не превышает 0,1Н, где Н – напор жидкости над центром тяжести отверстия, Рн = Рк (рис. 8.1).
Если линейный размер d отверстия значительно больше толщиныстенки d, в которой оно сделано (d > 3d), то такое отверстие называется отверстием в тонкой стенке. При этом считается, что края отверстияимеют острую кромку и при прохождении жидкости через такие отверстия практически отсутствуют потери напора на трение.
При образовании струи, вытекающей из отверстия, имеет место ее сжатие на расстоянии (0,5¸1,0)d от дна стенки или сосуда (рис. 8.1, а, б).
Рис. 8.1. Истечение жидкости из отверстий
Отношение площади сжатого сечения струи wс к площади отверстия w0 называется коэффициентом сжатия струи e.
e = wс/w0, (8.1)
Применив уравнение Бернулли к двум сечениям Н-Н (свободная поверхность жидкости в сосуде)и С-С (сжатое сечение), получим формулу для определения скорости движения жидкости при Н = const
, (8.2)
где Н — напор жидкости над отверстием;
– коэффициент скорости для отверстия;
z – коэффициент сопротивления отверстия, учитывающий потери напора от сечения Н-Н до сечения С-С.
Расход жидкости, вытекающей из отверстия, определяется по формуле
Q = wc×Vc. (8.3)
Подставляя в (8.3) значения wc и Vc, определенный из (8.1) и (8.2), получим:
, (8.4)
где m = ej, m — коэффициент расхода.
Величины коэффициентов e, j, z, m зависят от формы отверстия и режима движения жидкости, определяемого числом Rе.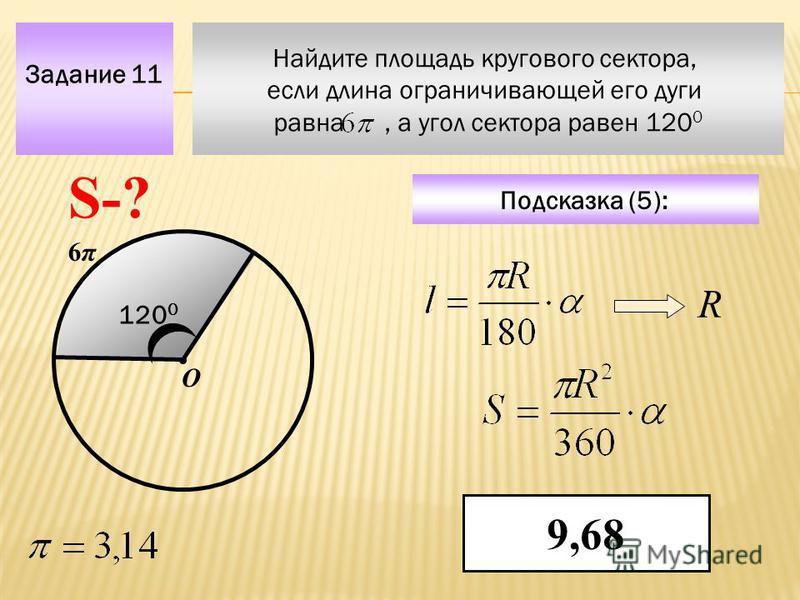
Рассмотрим процесс истечения жидкости через насадок.
Насадком называется короткий патрубок, присоединенный к отверстию, длина которого составляет l = (8¸4)d, где d – диаметр выходного отверстия в стенке.
В технике применяются следующие типы насадков (рис.8.2): цилиндрические, конические, коноидальные.
Рис. 8.2. Типы насадков:
1 – цилиндрический внешний; 2 – цилиндрический внутренний; 3 – конический сходящийся; 4 – конический расходящийся; 5 – коноидальный
Цилиндрические, конические сходящиеся и коноидальные насадки способствуют увеличению расхода вытекающей жидкости, по сравнению с истечением из отверстия. Это объясняется тем, что при входе в насадок происходит сжатие струи, а затем постепенное ее расширение с заполнением всего сечения насадка. Вследствие сжатия струи в насадке образуется вакуум, при этом возрастает действующий напор, т. к. истечение происходит не в атмосферу, а в область вакуума (рис.8.3).
к. истечение происходит не в атмосферу, а в область вакуума (рис.8.3).
Скорость вытекающей из насадка жидкости определяется по формуле
, (8.5)
где — коэффициент скорости для насадка; xн — коэффициентсопротивления насадка.
Рис. 8.3. Истечение жидкости через насадок
Формула для определения расхода Q при истечении жидкости из насадка имеет вид
, (8.6)
где w0 — площадь сечения выходного отверстия насадка; m— коэффициент расхода, величина которого зависит отвида насадка или его конфигурации;
– приведенный напор.
Коэффициенты j, e, z, m определяются опытным путем, их средние значения приведены в справочной литературе по гидравлике.
Литература
Основная:
1. Гукасов Н.А. Механика жидкости и газа. — М.: Недра, 1993.—416c.
Гукасов Н.А. Механика жидкости и газа. — М.: Недра, 1993.—416c.
2. Гейер В.Г, и др. Гидравлика и гидропривод. — М.: Недра, 1991.—331с.
3. Басниев К.С. и др. Подземная гидромеханика. — М.: Недра, 1993.—416с.
4. Арустамова Ц.Т., Иванникова В.Г., Гидравлика. — М.: Недра, 1995.—198с.
5. Альтшуль А.Д., Животовский А.С., Иванов И.П. Гидравлика и аэродинамика. — М.: Стройиздат, 1987.—414с.
6. Рабинович Е,3., Евгеньев А.Е. Гидравлика. — М.: Недра, 1987.—227c.
7. Сборник задач по гидравлике и газодинамике для нефтяных вузов./ Под ред. Г.Д. Розенберга. — М.: Недра, 1990.—238с.
8. Башта Т. М. и др. Гидравлика, гидромашины и гидроприводы. — М.: Машиностроение, 1982.—423с.
9. Чугаев Р.Р. Гидравлика (техническая механика жидкости). — Л.: Энергоиздат, 1982. —587с.
Дополнительная:
1. Розенберг Г.Д., Иванникова В.Г. Техническая гидромеханика. — М.: ЦИНГ, 1989.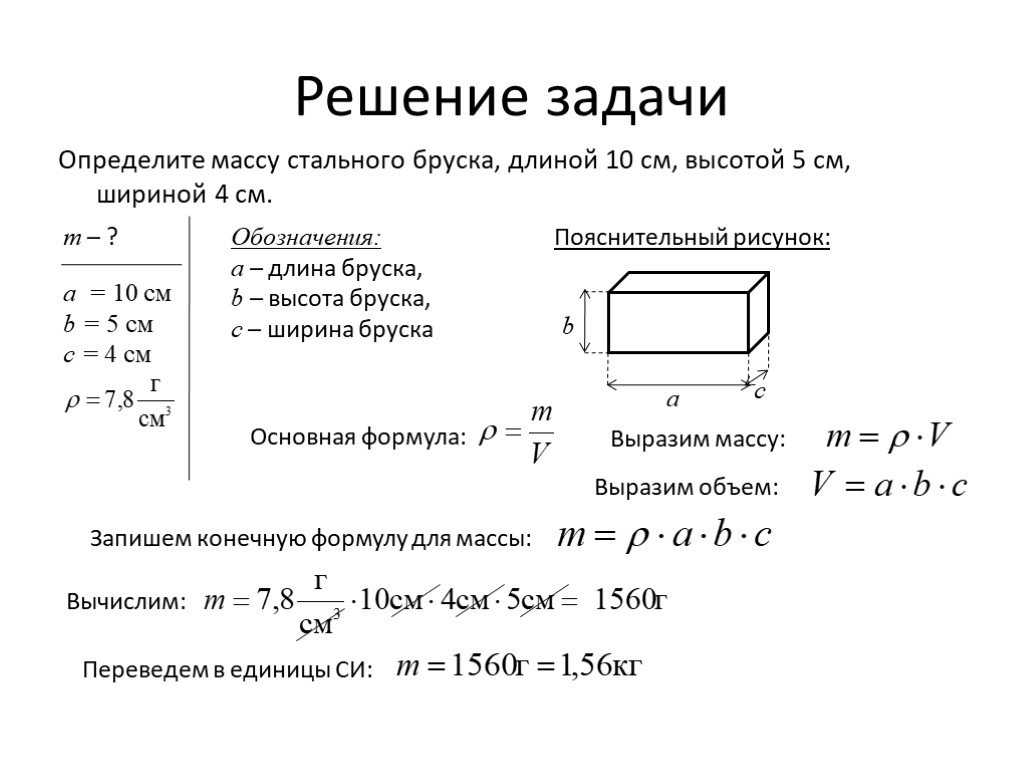 —132с.
—132с.
2. Сборник задач по машиностроительной гидравлике./ Под ред. И.И. Куколевского. — М.: Машиностроение, 1981.—464с.
3. Ибатулов К.А. Гидравлические машины и механизмы нефтяной промышленности. — М.: 1972.—208с.
4. Шищенко Р.И., Есьман Б.И. Практичекая гидравлика в бурении. — M.: Недра, 1969.—319c.
5. Лабораторный курс гидравлики, и гидропередач./ Под ред. С.С. Руднева и Л.Г. Подвидза. — М.: Машиностроение, 1984.—416c.
6. Гидравлика: Методические указания и контрольные задания для студентов — заочников инженерно-технических специальностей вузов./ И.А. Гилинский. — 4-е изд. — М.: Высш. шк., 1990.—62с.
7. Гидравлика, гидравлические машины и гидроприводы: Методические указания и контрольные задания для студентов заочников инженерно-технических специальностей вузов./ В.П. Норкус и др. — 5-е изд. — М.: Высш. шк., 1989.—56с.
8. Потёмина Т.П. Методические указания к курсовой работе по дисциплине «Гидрамеханика» для специальности 0906 — НГР и 0907 — НТХ очной и заочной формы обучения.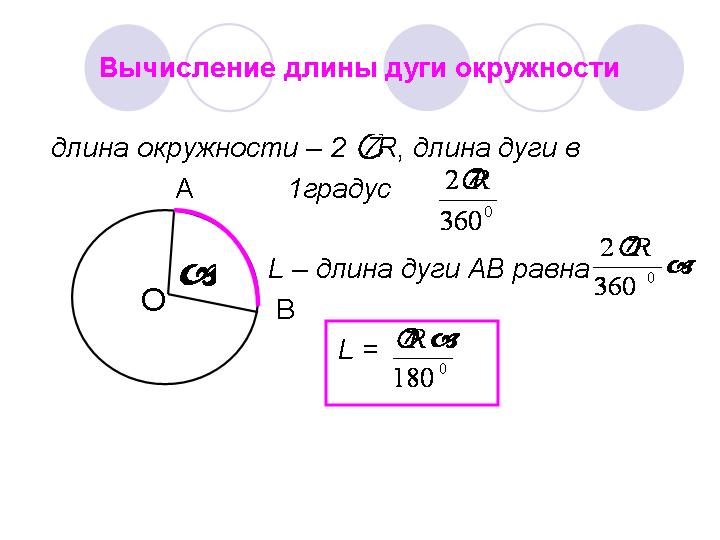 Тюмень. — 2000г.
Тюмень. — 2000г.
9. Потёмина Т.П. Методические указания к курсовому проекту на тему «Совместная работа пласта и скважины». Тюмень. — 1995г.
10. Методические указания к лабораторным работам по гидромеханике. /Под ред. Антипьева В.Н. — ТюмГНГУ, 1997.—58с.
11. Двинина И.С., Кудрявцева Н.А. Методические указания «Гидравлический расчёт простых гидропроводов». — Тюмень 1989.—46с.
12. Аэродинамика в вопросах и задачах /Под ред. Н.Ф. Краснова. — М.: Высшая школа, 1985.
13. Дейч М.Е. Техническая газодинамика. М.: Энергия, 1974.
14. Емцев Б.Т. Техническая гидромеханика. М.: Машиностроение, 1987.
15. Сборник задач по машиностроительной гидравлике /Под ред. И.И. Куколевского и Л.Г. Подвидза. -М.: Машиностроение, 1981.
16. Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1987.
17. Тугунов П.И., Новоселов В.Ф. Типовые расчеты при проектировании и эксплуатации нефтебаз и нефтепроводов. М.: Недра, 1981.
М.: Недра, 1981.
18. Чарный И.А. Основы газовой динамики. М.: Гостоптехиздат, 1961.
19.Яблонский B.C., Исаев ИА. Сборник задач и упражнений по технической гидромеханике. М.: Физматгиз, 1963.
20.Калицун В.И., Дроздов Е.в. и др. Основы гидравлики и аэродинамики. М.: Стройиздат, 2002. – 296с.
Содержание
Введение…………………………………………………………..……….……..3
I. Курс лекций………………………………………………….………………..5
1. Основные свойства жидкости и газа. Гидростатика ……………….…….……5
1.1. Основные свойства жидкости ………………………………..……….5
1.2 Физические свойства газа ………………………………….……..….10
1.3 Давление в покоящейся жидкости ……………………………….…..15
1.4 Сила статического давления жидкости на плоскую стенку ……….17
1.5 Сила статического давления жидкости на криволинейные
стенки. Закон Архимеда ……………………………………. ..…………………19
..…………………19
1.6 Относительный покой жидкости ………………………..……..……22
1.6.1 Прямолинейное равноускоренное движение сосуда …………….22
1.6.2 Равномерное вращение сосуда вокруг вертикальной оси ………24
2. Основные понятия кинематики и динамики жидкости ……………..……26
3. Режимы движения жидкости и основы гидродинамического подобия ….29
4. Основные законы движения газа …………………………………..…..…..32
5. Гидравлические сопротивления …………………………………..……..…35
6. Гидравлический расчет простых напорных трубопроводов ………………38
7. Гидравлический расчет сложных трубопроводов …………………..……..42
8. Истечение жидкости через отверстия и насадки ………………………….43
9. Гидравлический удар в трубопроводах ……………………………..…..…49
10. Движение неньютоновских жидкостей в трубах …………………………51
Приложения……………………………………………………….….…..…55
II.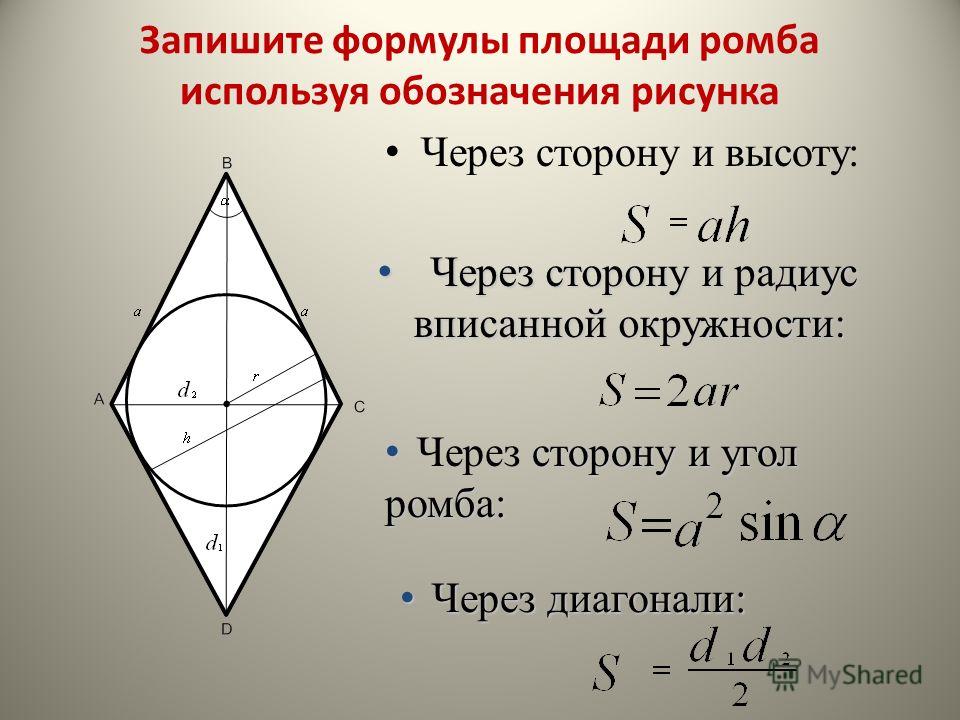 Задания для выполнения контрольных работ
Задания для выполнения контрольных работ
студентами – заочниками ………………………………………..……..….….57
Вариант 1…………………………………………………………….…….……57
Задачи ………………………………………………………………….…..……57
Приложения к задачам варианта 1 ………….……………….…………….… 71
Вариант 2 …………………………………………………………….….………73
Задачи………………………………………………………………….…..…….73
Приложения к задачам варианта 2………………………………………..…..85
Дата добавления: 2016-11-26; просмотров: 3287; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Площадь отверстия
Насыщенные пары и жидкости. В сосуд налита ртуть. Какая масса т ртути останется в сосуде? Под действием поверхностного натяжения свободная поверхность капель жидкости стремится принять шарообразную форму, соответствующую наименьшей поверхностной энергии и наименьшей площади свободной поверхности. Их форма тем ближе к шаровой, чем меньше вес капель, поскольку для малых капель сила поверхностного натяжения превосходит силу тяжести.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Стеноз митрального клапана (левого атриовентрикулярного отверстия)
- Стеноз митрального клапана (левого атриовентрикулярного отверстия)
- Площадь круга
- Площадь круга, онлайн расчет
- Вы точно человек?
- Площадь выходного отверстия
- Расчёт площади перфорации и количества отверстий на м2
- МИТРАЛЬНЫЙ КЛАПАН
- 9,5 мм деревообработка площадь отверстие увидел сверло площадь долото долото долото сверло
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Удивительные примеры логики
Состояние отпатрулирована. Негладкая замкнутая кривая , ограничивающая эту фигуру, также называется треугольником Рёло. Треугольник Рёло является простейшей после круга фигурой постоянной ширины [1]. Это расстояние называется шириной треугольника Рёло. Среди прочих фигур постоянной ширины треугольник Рёло выделяется рядом экстремальных свойств: наименьшей площадью [1] , наименьшим возможным углом при вершине [4] , наименьшей симметричностью относительно центра [5]. Название фигуры происходит от фамилии немецкого механика Франца Рёло.
Круг окружность — геометрическая фигура на плоскости, все точки которой равноудалены от данной точки центр круга. Формула площади круга: , где r — радиус круга, d — диаметр.
9,5 мм деревообработка площадь отверстие увидел сверло площадь долото долото долото сверло
Используя этот онлайн калькулятор, вы сможете найти площадь круга зная его радиус, диаметр или длину окружности.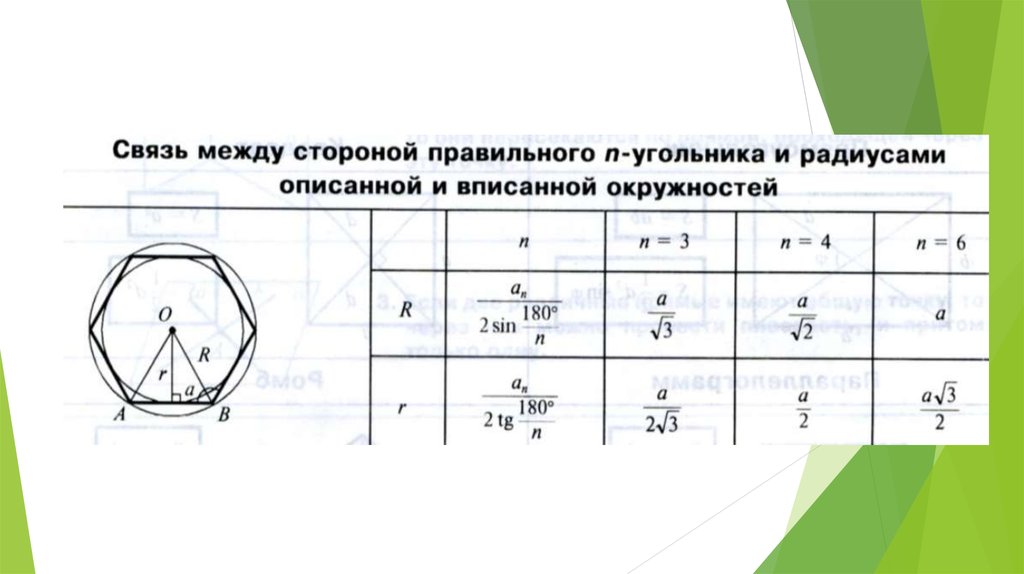 Воспользовавшись онлайн калькулятором для вычисления площади круга, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал. В онлайн калькулятор вводить можно числа или дроби 3, 0. Более подробно читайте в правилах ввода чисел. Если у вас возникли трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади. Вводить можно числа или дроби
Воспользовавшись онлайн калькулятором для вычисления площади круга, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал. В онлайн калькулятор вводить можно числа или дроби 3, 0. Более подробно читайте в правилах ввода чисел. Если у вас возникли трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади. Вводить можно числа или дроби
Строительство дома начинается с фундамента, который, как известно, должен быть надежным и крепким. Но многие забывают о таком важном моменте как вентиляционные отверстия. Особенно это актуально для ленточных сплошных фундаментов. В этой статье мы расскажем для чего нужны вентиляционные отверстия в фундаменте, как их сделать, какого размера они должны быть и стоит ли закрывать их на зиму.
Расчет количества шпурового заряда на основе трехмерной твердотельной модели взрываемой горной массы
Введение
Интеллектуальная буровая установка может точно получить литологические данные зоны взрывных работ. Насущная проблема, которую необходимо исследовать, разработать и решить, заключается в том, как в полной мере использовать литологические данные района взрывных работ, точно рассчитать объем различных горных массивов и усовершенствовать метод расчета заряда шпуров для повышения производительности. взрывной эффект и снизить стоимость взрывных работ. В настоящее время многие ученые провели много исследований по интеллектуальному распознаванию литологии. Гохэ Ли и др. предложил новый метод идентификации литологии, который использует несколько точек отбора проб геологических данных в качестве входных данных. Из сравнения эксперимента видно, что алгоритм SGAN-G может эффективно использовать неразмеченные данные для достижения более высокой точности предсказания литологии 1 . Саху и др. установил и предложил традиционную искусственную нейронную сеть (ANN-GDM), основанную на обучении по импульсу градиентного спуска, и традиционный генетический алгоритм (GA), основанный на методе генетического алгоритма искусственной нейронной сети (ANN-GA) 2 .
Насущная проблема, которую необходимо исследовать, разработать и решить, заключается в том, как в полной мере использовать литологические данные района взрывных работ, точно рассчитать объем различных горных массивов и усовершенствовать метод расчета заряда шпуров для повышения производительности. взрывной эффект и снизить стоимость взрывных работ. В настоящее время многие ученые провели много исследований по интеллектуальному распознаванию литологии. Гохэ Ли и др. предложил новый метод идентификации литологии, который использует несколько точек отбора проб геологических данных в качестве входных данных. Из сравнения эксперимента видно, что алгоритм SGAN-G может эффективно использовать неразмеченные данные для достижения более высокой точности предсказания литологии 1 . Саху и др. установил и предложил традиционную искусственную нейронную сеть (ANN-GDM), основанную на обучении по импульсу градиентного спуска, и традиционный генетический алгоритм (GA), основанный на методе генетического алгоритма искусственной нейронной сети (ANN-GA) 2 .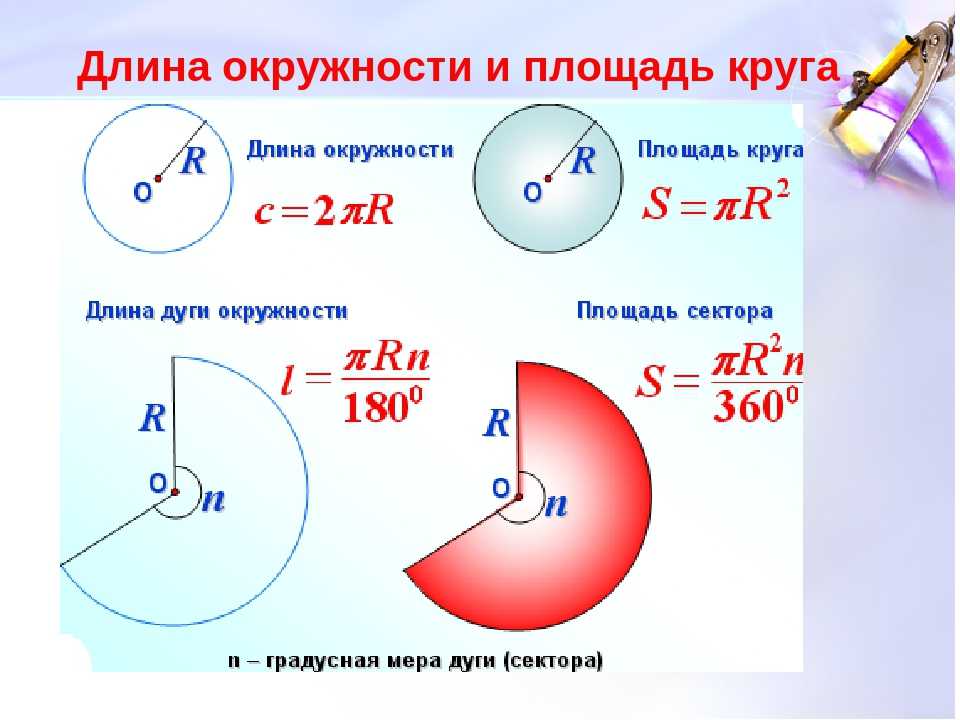 Сантос и др. оценили преимущества методов, основанных на ансамблях классификаторов нейронных сетей — наборах нейронных сетей, работающих совместно для достижения консенсуса в решении задачи распознавания литологии 3 . Шао и др. предположил, что алгоритм нейронной сети BP обладает характеристиками высокой точности идентификации и высокой скорости идентификации, что подходит для идентификации геологических исследований, таких как петрология, прогнозирование месторождений, идентификация горных пород и минералов и т. д. 4 . Чжан и др. предложил метод идентификации литологии для вулканического резервуара, который работает с каротажными данными путем объединения анализа основных компонентов и метода нейронной сети SOM для эффективного улучшения производительности нейронной сети 5 .
Сантос и др. оценили преимущества методов, основанных на ансамблях классификаторов нейронных сетей — наборах нейронных сетей, работающих совместно для достижения консенсуса в решении задачи распознавания литологии 3 . Шао и др. предположил, что алгоритм нейронной сети BP обладает характеристиками высокой точности идентификации и высокой скорости идентификации, что подходит для идентификации геологических исследований, таких как петрология, прогнозирование месторождений, идентификация горных пород и минералов и т. д. 4 . Чжан и др. предложил метод идентификации литологии для вулканического резервуара, который работает с каротажными данными путем объединения анализа основных компонентов и метода нейронной сети SOM для эффективного улучшения производительности нейронной сети 5 .
Многие ученые провели много исследований по трехмерному твердотельному моделированию. Sun представляет быстрый самоадаптирующийся и усовершенствованный метод интерполяции, взвешенной по расстоянию, в зависимости от характеристик данных скважинных проб 6 . Сонг и др. создал метод полуавтоматического 3D-моделирования и визуализации сложных геологических тел, объединив типичные системы ГИС с программным обеспечением для 3D-моделирования, таким как ArcGIS и SketchUp 7 . Лю ввел понятие «корреляционное расстояние» для анализа корреляций между значениями геологической высоты скважины и рассчитал корреляционные расстояния для каждой отметки пласта 8 . Джиа и др. предложил усовершенствованный многомасштабный метод интерполяции на основе анизотропии, применяемый для эффективного моделирования поверхности угольного пласта 9 . Че предложил Трехмерное геологическое моделирование угольных пластов с использованием взвешенного метода Кригинга и данных из нескольких источников 10 . Чтобы преодолеть существующий в настоящее время разрыв между твердотельными моделями AutoCAD и областью моделирования сетки, Маршаллингер создал программу Visual LISP, которая преобразует твердотельные модели AutoCAD в массивы вокселей 9.
Сонг и др. создал метод полуавтоматического 3D-моделирования и визуализации сложных геологических тел, объединив типичные системы ГИС с программным обеспечением для 3D-моделирования, таким как ArcGIS и SketchUp 7 . Лю ввел понятие «корреляционное расстояние» для анализа корреляций между значениями геологической высоты скважины и рассчитал корреляционные расстояния для каждой отметки пласта 8 . Джиа и др. предложил усовершенствованный многомасштабный метод интерполяции на основе анизотропии, применяемый для эффективного моделирования поверхности угольного пласта 9 . Че предложил Трехмерное геологическое моделирование угольных пластов с использованием взвешенного метода Кригинга и данных из нескольких источников 10 . Чтобы преодолеть существующий в настоящее время разрыв между твердотельными моделями AutoCAD и областью моделирования сетки, Маршаллингер создал программу Visual LISP, которая преобразует твердотельные модели AutoCAD в массивы вокселей 9. 0005 11 . Однако из-за незрелого развития интеллектуальных буровых установок ни один специалист не занимается трехмерным твердотельным моделированием взрывных работ горной массы.
0005 11 . Однако из-за незрелого развития интеллектуальных буровых установок ни один специалист не занимается трехмерным твердотельным моделированием взрывных работ горной массы.
Чтобы снизить стоимость взрывных работ при одновременном улучшении эффекта взрыва, многие ученые и инженеры провели множество исследований по вспомогательному методу расчета заряда шпуров. Ли в соответствии с теорией эквивалентного сопротивления разрушению породы для столбчатого заряда, теорией Ливингстона о воронке от взрыва и линейной плотностью была применена для вывода теоретической формулы расчета глубины взрывной скважины в прогрессивной спиральной выемке 12 . Ван взял в качестве примера строительство золотого рудника Пайшаньлоу в Ляонине, провел анализ и расчет методов определения и практических данных различных параметров буровзрывных работ в сочетании с общими инженерными условиями, такими как линия сопротивления ходовой части, шаг, расстояние между рядами, сверхглубокие стоимость бурения и количество заряда взрывной скважины 13 .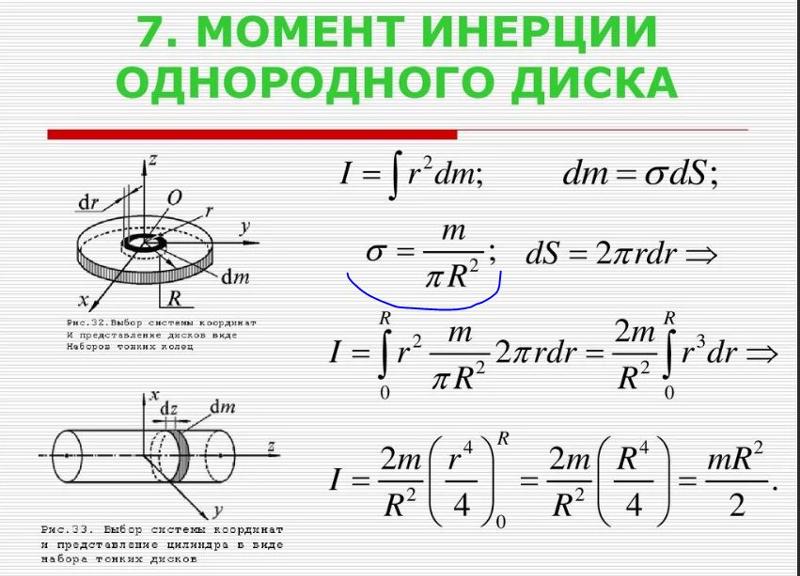 Адхикари и др. обобщив опыт и методику расчета удельного заряда при проектировании карьерных взрывных работ, установили, что на удельный заряд существенное влияние оказывает требуемая степень дробления, распределения, передачи и использования энергии взрывчатого вещества 14 . Шим оценил скальный фактор по геологическим данным, а метод последовательного индикаторного моделирования предсказал его трехмерное пространственное распределение. Весь рассматриваемый карьер был классифицирован по трем типам горной массы, и для каждого типа была предложена оптимальная схема взрывных работ на основе трехмерного пространственного распределения горного фактора. Можно сделать вывод, что можно спроектировать схему взрывных работ для достижения минимальных производственных затрат при крупномасштабных разработках карьеров путем прогнозирования фрагментации породы на основе трехмерного пространственного распределения коэффициента породы 9.0005 15 . В настоящее время большинство широко используемых методов расчета заряда взрывных скважин основаны на литологических данных или опыте разведочных скважин для получения литологического распределения.
Адхикари и др. обобщив опыт и методику расчета удельного заряда при проектировании карьерных взрывных работ, установили, что на удельный заряд существенное влияние оказывает требуемая степень дробления, распределения, передачи и использования энергии взрывчатого вещества 14 . Шим оценил скальный фактор по геологическим данным, а метод последовательного индикаторного моделирования предсказал его трехмерное пространственное распределение. Весь рассматриваемый карьер был классифицирован по трем типам горной массы, и для каждого типа была предложена оптимальная схема взрывных работ на основе трехмерного пространственного распределения горного фактора. Можно сделать вывод, что можно спроектировать схему взрывных работ для достижения минимальных производственных затрат при крупномасштабных разработках карьеров путем прогнозирования фрагментации породы на основе трехмерного пространственного распределения коэффициента породы 9.0005 15 . В настоящее время большинство широко используемых методов расчета заряда взрывных скважин основаны на литологических данных или опыте разведочных скважин для получения литологического распределения.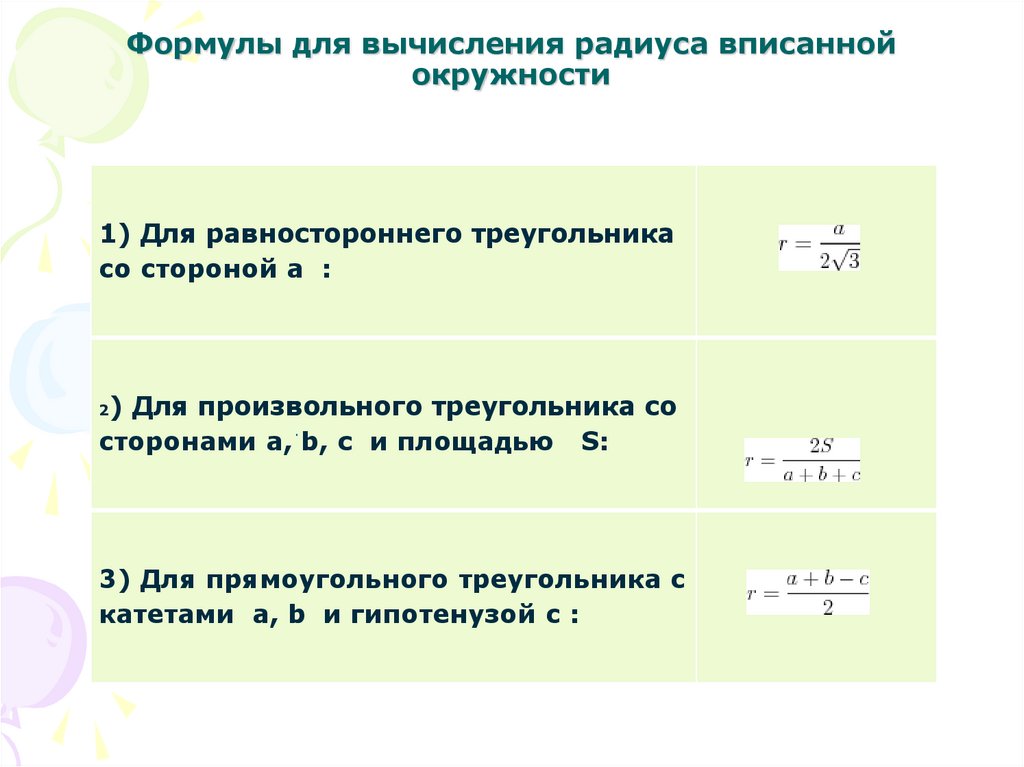 Из-за высокой плотности размещения разведочных скважин распределение литологии в районе взрывных работ является неточным, что часто приводит к значительным отклонениям от схемы взрывных работ. Способ расчета заряда шпура на основе трехмерной твердотельной модели взорванной горной массы заключается в полном использовании литологических данных взорванной горной массы для создания точной трехмерной твердотельной модели взорванной горной массы и расчета взрывной скважины. заряд на основе точной трехмерной твердотельной модели, улучшающий эффект взрывных работ и снижающий стоимость взрывных работ.
Из-за высокой плотности размещения разведочных скважин распределение литологии в районе взрывных работ является неточным, что часто приводит к значительным отклонениям от схемы взрывных работ. Способ расчета заряда шпура на основе трехмерной твердотельной модели взорванной горной массы заключается в полном использовании литологических данных взорванной горной массы для создания точной трехмерной твердотельной модели взорванной горной массы и расчета взрывной скважины. заряд на основе точной трехмерной твердотельной модели, улучшающий эффект взрывных работ и снижающий стоимость взрывных работ.
Этот документ состоит из четырех частей: первая часть в основном представляет идентификацию литологии и создание базы данных взрывных скважин, вторая часть в основном представляет метод расчета количества заряда взрывных скважин, а третья часть в основном представляет метод расчета, основанный на трехмерная твердотельная модель взрыва горного массива. Наконец, метод расчета количества шихты применяется в качестве примера на угольном разрезе Xilinhot Shengli в автономном районе Внутренняя Монголия, Китай.
Идентификация литологии и создание базы данных взрывных скважин
Данные о взрывных скважинах горной породы, собранные с интеллектуальной буровой установки, хранятся в файлах, и создается база данных для хранения, дальнейшего управления и применения данных о взрывных скважинах.
Структура данных взрывной скважины
Первые семь строк данных, собранных с интеллектуальной буровой установки, записывают номер бурения, статус буровой установки, номер буровой установки, время загрузки, долготу, широту и высоту соответственно. Строки с 8 по 16 представляют собой записи секции каменной колонны. Эти данные включают номер бурения, глубину бурения, скорость вращения, перепад давления вращения, давление наддува 1, давление наддува 2, скорость бурения, давление ветра и идентифицированную литологию. Впоследствии эти данные записи будут распространяться для каждого скального столба до тех пор, пока взрывная скважина не будет завершена. Данные, приведенные в таблице 1, являются данными разреза скального целика с номером взрывной скважины 0620171118170059.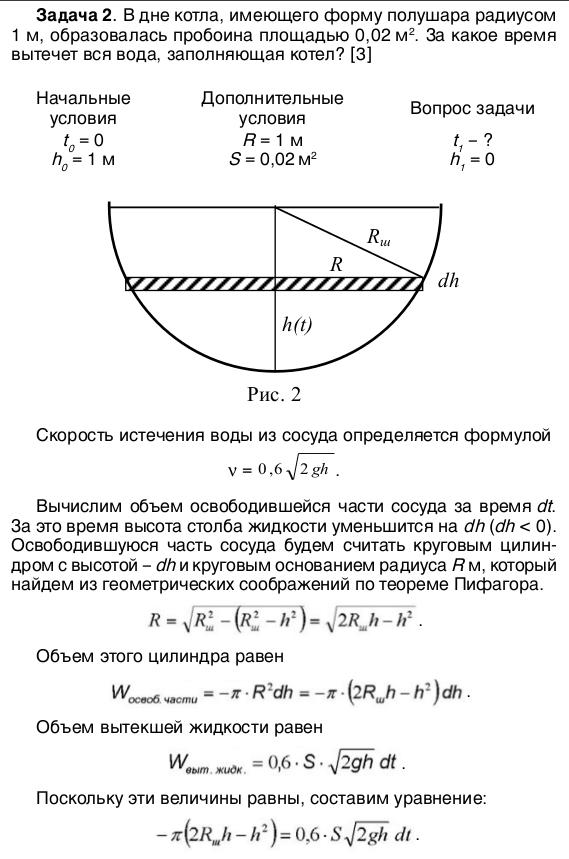 собранные интеллектуальной дрелью. Эти данные составляют файлы данных взрывных скважин, но эти файлы данных не удобны для управления и дальнейшего применения. Необходимо создать базу данных для хранения и управления этими данными.
собранные интеллектуальной дрелью. Эти данные составляют файлы данных взрывных скважин, но эти файлы данных не удобны для управления и дальнейшего применения. Необходимо создать базу данных для хранения и управления этими данными.
Таблица 1 Данные взрывных скважин.
Полноразмерная таблица
Проектирование базы данных взрывных скважин
Использование Microsoft Access для создания базы данных взрывных скважин и создание трех таблиц данных в базе данных: таблица взрывных скважин (отверстие), таблица данных взрывных скважин (данные) и таблица литологии (рок), используемый для хранения данных, собранных с интеллектуальных буровых установок. Взаимосвязь между этими тремя таблицами данных показана на рис. 1. Таблица взрывных скважин (отверстие) связана с таблицей данных взрывных скважин (данные) черезhole_id, а таблица литологии (порода) связана с данными взрывных работ. -таблица данных отверстия (данные) через rock_id.
Рисунок 1
Связь между таблицами данных.
Изображение в полный размер
Извлечение данных о взрывных скважинах
При извлечении данных о взрывных скважинах из файлов данных в базу данных о взрывных скважинах необходимо преобразовать координаты взрывных скважин, выраженные долготой и широтой взрывной скважины, в x , у координаты. Полученная таблица взрывных скважин, таблица данных взрывных скважин и таблица литологии показаны в таблицах 2, 3 и 4 соответственно.
Таблица 2 Таблица взрывных скважин.
Полноразмерный стол
Таблица 3 Паспорт взрывных скважин.
Полноразмерная таблица
Таблица 4 Литологические данные.
Полноразмерная таблица
Метод расчета количества шпурового заряда
В настоящее время взрывные работы широко используются в гражданском, водном хозяйстве, гидроэнергетике, на транспорте и в других областях строительства 16,17,18 . При открытых горных работах взрывные работы являются одним из важнейших бизнес-процессов технологии открытых горных работ 19,20,21,22,23 , что связано с производственными мощностями и экономическими преимуществами добычи открытым способом. Следовательно, при проектировании производства взрывных работ необходимо быть максимально точным и эффективным, чтобы добиться лучшего эффекта взрывных работ для удовлетворения требований высокоэффективного производства на месте. Поэтому расчет количества шпурового заряда является основополагающим, а общепринятая формула для расчета конструкции взрывных работ выглядит следующим образом: 24 :
Следовательно, при проектировании производства взрывных работ необходимо быть максимально точным и эффективным, чтобы добиться лучшего эффекта взрывных работ для удовлетворения требований высокоэффективного производства на месте. Поэтому расчет количества шпурового заряда является основополагающим, а общепринятая формула для расчета конструкции взрывных работ выглядит следующим образом: 24 :
$$Q = qawh,$$
(1)
где Q — количество шпурового заряда, кг; q – пороховой фактор, кг/м 3 ; а – шаг, м; w – нагрузка, м; h — высота уступа, м.
Исходя из приведенной выше формулы расчета количества взрывчатых веществ, чтобы приблизить рассчитанное общее количество зарядов взрывчатых веществ к фактическому количеству заряда, необходимому для высокоэффективного взрывания, выбор удельного расхода взрывчатых веществ q должен быть очень строгим. Это очень сложно для компаний, у которых нет данных о долгосрочном производственном опыте в качестве параметров. Неправильное значение удельного расхода ВВ q часто приводит к неточному расчету количества заряда, что приводит к недостаточному заряду или остаточному заряду при взрывных работах, что сказывается на эффективности взрывных работ.
Неправильное значение удельного расхода ВВ q часто приводит к неточному расчету количества заряда, что приводит к недостаточному заряду или остаточному заряду при взрывных работах, что сказывается на эффективности взрывных работ.
Трехмерная твердотельная модель шпурового заряда
Создание трехмерной твердотельной модели зоны взрывных работ
Интерполировать для создания трехмерной твердотельной модели горного массива
Сегодня многие ученые занимаются трехмерным твердотельным моделированием 25,26,27,28,29,30,31,32 . Метод интерполяции обратного квадрата расстояния имеет хорошую универсальность и доступен в случае отсутствия пластов и крайне неравномерного распределения ствола скважины, а ошибка интерполяции относительно мала, поэтому используется метод интерполяции обратного квадрата расстояния 33 . Метод обратного квадрата расстояния является своего рода методом интерполяции, связанным с пространственным расстоянием. При расчете значения точек интерполяции по принципу, что чем ближе расстояние, тем больше значение веса, для подбора значения оцениваемых баллов используется линейное взвешивание нескольких соседних точек 9{p} }}}},$$
При расчете значения точек интерполяции по принципу, что чем ближе расстояние, тем больше значение веса, для подбора значения оцениваемых баллов используется линейное взвешивание нескольких соседних точек 9{p} }}}},$$
(2)
где г — расчетная стоимость; г i — i-я проба; d i — расстояние; p — степень расстояния, ее значение существенно влияет на результат оценочной величины.
Зона дробеструйной обработки делится на множество твердых блоков в соответствии с заданной длиной, шириной и высотой твердого блока, получая набор твердых элементов (E_{0} = { e_{1} , e_{2} ,ldots , e_{i} , ldots e_{n} }) всей площади взрыва. При этом (e_{i}) — i-я твердая единица, (i in [1,;n]), n — общее количество твердых единиц. Взяв данные распределения литологии взрывной скважины в качестве образца, используйте метод обратных квадратов расстояния для выполнения литологической интерполяции для каждой твердотельной единицы в наборе твердых единиц (E{}_{0}) и назначьте литологию каждой твердотельной единице для создания трехмерная модель массива горных пород.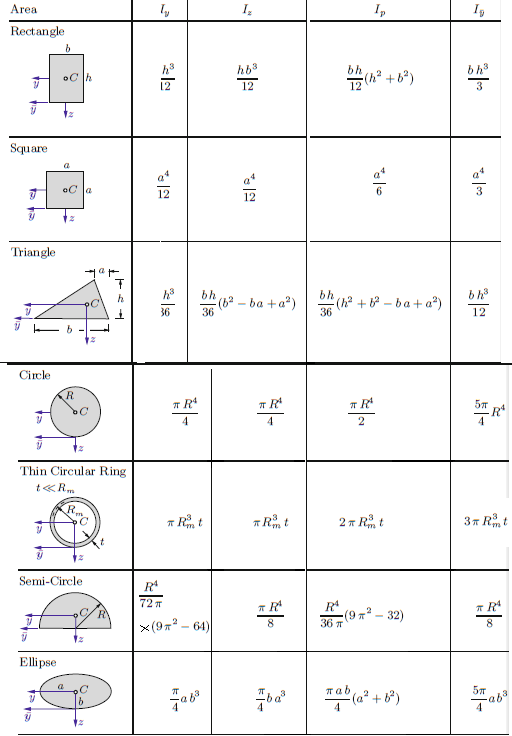 {prime}}}) это 9{prime} in left[ {1,;l} right]), l — общее количество треугольников полигона полигона; набор треугольников области взрывных работ (T_{b}) используется для вырезания набора единиц объектов (E_{0}) зоны взрывных работ, а трехмерный объект горной массы в зоне взрывных работ сохраняется, записывается как (E_{1}).
{prime}}}) это 9{prime} in left[ {1,;l} right]), l — общее количество треугольников полигона полигона; набор треугольников области взрывных работ (T_{b}) используется для вырезания набора единиц объектов (E_{0}) зоны взрывных работ, а трехмерный объект горной массы в зоне взрывных работ сохраняется, записывается как (E_{1}).
Треугольная резка твердотельной модели в ступени забоя
Триангуляция линии ступени забоя 38,39,40 для получения набора треугольников (T_{c} = { t_{1} , t_{2} , ldots , t_{j} , ldots t_{m} }). При этом (t_{j}) — j-й треугольник шага захода, (j in [1,;m]), (m) — общее количество треугольников для шагов захода; использовать набор треугольников забоя (T_{c}) для вырезания набора трехмерных объектов горной массы (E_{1}) в пределах диапазона взрывных работ и сохранить трехмерный объект горной массы ниже ступенчатого треугольника забоя, а именно трехмерная твердотельная модель массива горных пород в зоне взрывных работ, записанная как (E = left{ {e_{1} ,;e_{2} , ldots ,e_{{j^{prime}} } , ldots e_{k} } right}). {prime} in [1,;k], ; k) — общее количество единиц объекта в зоне взрыва после резки.
{prime} in [1,;k], ; k) — общее количество единиц объекта в зоне взрыва после резки.
Рассчитать диапазон влияния взрывной скважины
Установить треугольную сетку точек взрывной скважины
Триангулировать набор точек положения взрывной скважины (P = { p_{1} , p_{2} , ldots , p_{f} , ldots p_{F} }) и вершины многоугольника области взрывания, то получаем набор треугольников взрывных скважин (T_{r} = left{ {t_{r1} , t_{r2} , ldots , t_{rh} , ldots t_{rH} } right}), среди них (p_{f}) — положение f-й взрывной скважины, (f in [1 ,F]), F – общее количество позиций шпуров в полигоне зоны взрывных работ, (t_{rh}) – h -й разделенный треугольник, (h in [1,H]), H — общее количество треугольников, полученных путем триангуляции точки положения взрывной скважины и вершин многоугольника зоны взрывных работ.
Получение полигона влияния взрывных скважин
Для каждой взрывной скважины из набора треугольников взрывных скважин (T_{r}) получаются все треугольники, связанные с точками положения взрывных скважин. Многоугольник влияния шпуров образуется путем последовательного соединения центральных точек, середин сторон или вершин связанных с ним треугольников. Набор всех полигонов влияния взрывных скважин обозначается как (PL = left{ {pl_{1} , pl_{2} , ldots , pl_{m} , ldots , pl_{F} } right} ), где (pl_{m}) — полигон влияния m-й взрывной скважины, (m in left[ {1,;F} right]). Метод получения полигона влияния взрывных скважин следующий:
Многоугольник влияния шпуров образуется путем последовательного соединения центральных точек, середин сторон или вершин связанных с ним треугольников. Набор всех полигонов влияния взрывных скважин обозначается как (PL = left{ {pl_{1} , pl_{2} , ldots , pl_{m} , ldots , pl_{F} } right} ), где (pl_{m}) — полигон влияния m-й взрывной скважины, (m in left[ {1,;F} right]). Метод получения полигона влияния взрывных скважин следующий:
-
1.
Если все три вершины треугольника, соединяющего взрывную скважину, являются точками взрывной скважины, центр треугольника считается вершиной многоугольника влияния взрывной скважины;
-
2.
Если только две из трех вершин треугольника, соединяющего шпуры, являются точками шпуров, то за вершину многоугольника влияния шпуров принимается средняя точка двух шпуров;
-
3.

Если только одна из трех вершин треугольника, соединяющего скважину, является точкой шпура, то две другие нескважинные точки треугольника принимаются за вершины многоугольника влияния шпура.
Соедините эти вершины, чтобы сформировать многоугольник влияния взрывной скважины. Как показано на рис. 2, полигон влияния, образующий взрывную скважину J взят в качестве примера для пояснения метода получения полигона влияния взрывной скважины. К шпуру J подключены точки A, B, C, D и E . Среди них A, B и C являются шпуровыми точками, а D и E не шурфовыми точками. Треугольники, соединенные этими вершинами: ∆ ABJ, ∆ JBC, ∆ JCD, ∆ JAE и ∆ JDE 9.0096 . Три вершины ∆ ABJ и ∆ JBC являются точками взрывных скважин, поэтому возьмем центральные точки G и H ∆ ABJ и ∆ JBC полигона взрывных скважин, влияющие на полигоны взрывных скважин. ; поскольку только две вершины ∆ JCD являются точками взрывных скважин, средняя точка I соединительной линии взрывных скважин JC используется в качестве вершины многоугольника влияния взрывных скважин. Аналогично возьмем среднюю точку F линии соединения двух взрывных скважин JA ∆ JAE в качестве вершины полигона влияния взрывных скважин; ∆ JDE имеет только одну вершину в качестве точки взрывной скважины, поэтому возьмите две другие точки треугольника без взрывных скважин D и E в качестве вершин многоугольника влияния взрывной скважины. Вершины полигона влияния взрывной скважины соединяются в полигон влияния взрывной скважины J , а набор его вершин равен (left{ {E,;D,;I,;H,;G, ;F,;E} right}).
; поскольку только две вершины ∆ JCD являются точками взрывных скважин, средняя точка I соединительной линии взрывных скважин JC используется в качестве вершины многоугольника влияния взрывных скважин. Аналогично возьмем среднюю точку F линии соединения двух взрывных скважин JA ∆ JAE в качестве вершины полигона влияния взрывных скважин; ∆ JDE имеет только одну вершину в качестве точки взрывной скважины, поэтому возьмите две другие точки треугольника без взрывных скважин D и E в качестве вершин многоугольника влияния взрывной скважины. Вершины полигона влияния взрывной скважины соединяются в полигон влияния взрывной скважины J , а набор его вершин равен (left{ {E,;D,;I,;H,;G, ;F,;E} right}).
Рисунок 2
Полигон влияния взрывной скважины.
Изображение в полный размер
Получение блока объекта, влияющего на взрывную скважину
Пересечение полигона влияния каждой скважины и трехмерной твердотельной модели горной массы в зоне выемки взрывных работ используется для получения твердотельного элемента влияния каждого взрыва отверстие.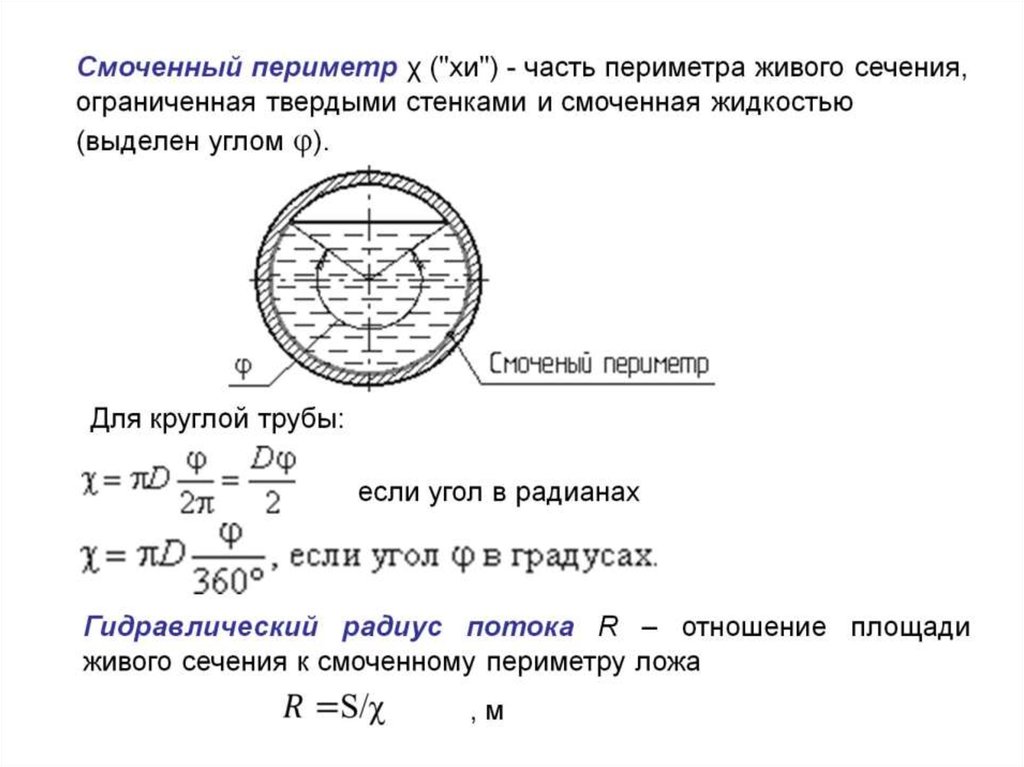 Предположим, что полигон влияния (pl_{m}) шпура м — -й скважины пересекается с трехмерной твердотельной моделью E массива горных пород в районе взрывных работ после резки, а множество влияющих объектов (C_ {m} = {c_{m1}, c_{m2}, ldots,c_{my}, ldots,c_{mr} }) из м -й взрывной скважины, где (c_{my}) — y- -я влияющая единица объекта м- -й взрывной скважины, (y in [1,;r] ), r — общее количество единиц воздействующего объекта м -й взрывной скважины.
Предположим, что полигон влияния (pl_{m}) шпура м — -й скважины пересекается с трехмерной твердотельной моделью E массива горных пород в районе взрывных работ после резки, а множество влияющих объектов (C_ {m} = {c_{m1}, c_{m2}, ldots,c_{my}, ldots,c_{mr} }) из м -й взрывной скважины, где (c_{my}) — y- -я влияющая единица объекта м- -й взрывной скважины, (y in [1,;r] ), r — общее количество единиц воздействующего объекта м -й взрывной скважины.
Рассчитайте количество заряда шпура
В соответствии с удельным расходом взрывчатого вещества (q_{x}), требуемым для различных литологий, рассчитайте количество взрывчатого вещества, необходимое для каждой единицы воздействующего объекта взрывной скважины, и просуммируйте требуемое количество взрывчатого вещества всеми влияющими единицами объекта взрывной скважины для получения количества заряда взрывной скважины, как показано в следующей формуле: 9{r} q_{x} v_{y} . $$
$$
(3)
Среди них (Q_{m}) — количество взрывчатого вещества, необходимое для бурения м -й взрывной скважины, ( v_{y}) — объем взрыва y-й единицы воздействующего объекта, а (q_{x}) — удельный расход взрывчатых веществ в x-й породе.
Практическое применение
На основе данных о распределении литологии зоны взрывных работ на угольном карьере Шэнли, Силиньхот, автономный район Внутренняя Монголия, Китай (как показано на рис. 3), в этой статье создается трехмерная модель области взрывных работ и осуществляет расчет количества шпурового заряда с помощью метода расчета количества шпурового заряда на основе трехмерной твердотельной модели взрываемой горной массы. Данное исследование усовершенствовано на базе гидравлической буровой установки LWD-200B (рис. 4а). Учитывая, что она имеет хороший уровень автоматизации в начале проектирования, остается избыточное пространство для трансформации интеллектуальной буровой установки, что значительно облегчает интеллектуальную трансформацию. Экран дисплея системы идентификации литологии связывается с контроллером через шину CAN, который может отображать рабочее состояние, информацию о неисправностях и страницу идентификации литологии буровой установки в режиме реального времени. Ручной ввод идентификационного номера литологии на этапе тестирования сбора данных также осуществляется через экран дисплея, как показано на рис. 4b.
Экран дисплея системы идентификации литологии связывается с контроллером через шину CAN, который может отображать рабочее состояние, информацию о неисправностях и страницу идентификации литологии буровой установки в режиме реального времени. Ручной ввод идентификационного номера литологии на этапе тестирования сбора данных также осуществляется через экран дисплея, как показано на рис. 4b.
Рисунок 3
Угольный разрез Шэнли, Силиньхот, Автономный район Внутренняя Монголия, Китай. Этот рисунок синтезирован Visio 2013 (https://www.microsoft.com/zh-cn/microsoft-365/previous-versions/microsoft-visio-2013), а также ( a ) и ( b ) в этот рисунок загружается картами Google (https://www.google.com/maps).
Увеличить
Рисунок 4
Система идентификации литологии интеллектуальной буровой установки: ( a ) Гидравлическая буровая установка LWD-200B; ( b ) система идентификации литологии.
Увеличить
Данные взрывных работ
Объем взрывных работ
Полигон взрывных работ расположен на уступе № 918 угольного разреза Шэнли в г. Силиньхот автономного района Внутренняя Монголия. Рабочий диапазон составляет 125 м в длину и 65 м в ширину, имеется 165 взрывных скважин.
Начертить положение взрывных скважин
Выберите диапазон на графике и нарисуйте на графике взрывные скважины выбранного диапазона. Точка на графике — это место взрывной скважины, и взрывные скважины отмечены. Результат показан на рис. 5. Шпуры, показанные на рисунке, относятся к №9.18 стендовых буровзрывных работ на угольном карьере Шэнли в Силиньхоте.
Изображение в полный размер
Начертить гистограмму взрывной скважины
Трехмерная гистограмма отображается в трехмерном виде, и отчетливо видны структурное распределение и удельная мощность пластов руды и породы внутри взрывной скважины, как показано на рис. 6. Трехмерная гистограмма всех взрывных скважин на скважине № 918 уступ угольного разреза в Силиньхоте показан на рис. 6а; трехмерная гистограмма одиночной взрывной скважины показана на рис. 6b. Породы разной литологии заполнены трехмерным телом разных цветов. Мощность горной породы и название литологии отмечены рядом с трехмерной каменной колонной. На рисунке представлена трехмерная гистограмма взрывной скважины ZK2032 с шестью слоями породы. От устья до забоя скважины название и мощность породы: аргиллит 4,8 м, углеродистый аргиллит 0,36 м, песчаный аргиллит 2,65 м, углеродистый аргиллит 1,61 м, песчаный аргиллит 1,36 м и углеродистый аргиллит 2,08 м.
6а; трехмерная гистограмма одиночной взрывной скважины показана на рис. 6b. Породы разной литологии заполнены трехмерным телом разных цветов. Мощность горной породы и название литологии отмечены рядом с трехмерной каменной колонной. На рисунке представлена трехмерная гистограмма взрывной скважины ZK2032 с шестью слоями породы. От устья до забоя скважины название и мощность породы: аргиллит 4,8 м, углеродистый аргиллит 0,36 м, песчаный аргиллит 2,65 м, углеродистый аргиллит 1,61 м, песчаный аргиллит 1,36 м и углеродистый аргиллит 2,08 м.
Рисунок 6
Трехмерная гистограмма взрывных скважин: ( a ) трехмерная гистограмма всех взрывных скважин; ( b ) Гистограмма скважины ZK2032.
Изображение в натуральную величину
Построение трехмерной твердотельной модели массива горных пород в зоне взрывных работ
Интерполирование твердотельной трехмерной модели
В пределах зоны взрывных работ она делится на множество кубических объектов на расстоянии 2 м (2 м в длину, ширина и высота), и каждый объект-куб используется как элемент твердотельной 3D-модели. За образец берутся литологические данные взрывной скважины. Метод обратного квадрата расстояния используется для интерполяции литологических данных каждого кубического элемента. Перед интерполяцией следует определить интерполированные скважины по положению элементов, которые можно разделить на два этапа: во-первых, найти все взрывные скважины в диапазоне по дальности поиска 40 м; во-вторых, определить интерполированные шпуры среди шпуров, полученных на первом этапе, по расстоянию от положения элемента от ближнего до дальнего и величине угла экранирования. Метод обратного квадрата расстояния используется для окончательного завершения создания трехмерной твердотельной модели, включая в общей сложности 51,975 объектов, как показано на рис. 7. Красный многоугольник — это полигон взрывных работ, а литология объектов на рисунке представлена цветом.
За образец берутся литологические данные взрывной скважины. Метод обратного квадрата расстояния используется для интерполяции литологических данных каждого кубического элемента. Перед интерполяцией следует определить интерполированные скважины по положению элементов, которые можно разделить на два этапа: во-первых, найти все взрывные скважины в диапазоне по дальности поиска 40 м; во-вторых, определить интерполированные шпуры среди шпуров, полученных на первом этапе, по расстоянию от положения элемента от ближнего до дальнего и величине угла экранирования. Метод обратного квадрата расстояния используется для окончательного завершения создания трехмерной твердотельной модели, включая в общей сложности 51,975 объектов, как показано на рис. 7. Красный многоугольник — это полигон взрывных работ, а литология объектов на рисунке представлена цветом.
Рисунок 7
Интерполированная трехмерная твердотельная модель.
Полноразмерное изображение
Вырезка полигона полигона взрывных работ
Возьмите полигон полигона взрывных работ для создания сетки полигона взрывных работ (рис. 8a), а трехмерная твердотельная модель интерполируется путем разрезания сетки полигона взрывных работ. Отрежьте внешние объекты сетки области видимости и сохраните внутренние объекты. Результат резки показан на рис. 8b.
8a), а трехмерная твердотельная модель интерполируется путем разрезания сетки полигона взрывных работ. Отрежьте внешние объекты сетки области видимости и сохраните внутренние объекты. Результат резки показан на рис. 8b.
Рисунок 8
Процесс резки решетки взрывного полигона: ( a ) Решетка взрывного полигона; ( b ) Твердая 3D-модель после резки.
Изображение в натуральную величину
Триангуляция сетки на поверхности забоя
Триангуляция сетки выполняется на линии уступа и измерительных точках забоя для построения треугольной сетки поверхности забоя (рис. 9а). Вырежьте трехмерную твердотельную модель взрывных работ с сеткой треугольника забоя, отрежьте объекты над сеткой треугольника забоя и сохраните объекты ниже (рис. 9).б). Процесс резки показан на рис. 9. Трехмерная модель дробеструйной обработки после резки состоит из 17 006 объектов.
Рисунок 9
Процесс резки забоя: ( a ) треугольная сетка забоя; ( b ) пескоструйная 3D-модель после резки.
Изображение полного размера
Рассчитать радиус действия взрывной скважины в зоне взрывных работ
В данном примере имеется 165 эффективных взрывных скважин. Согласно методу 3.2, данные, образованные эффективным положением устья взрывной скважины и многоугольником дальности взрывных работ, триангулируются для получения треугольной сетки дальности взрывных работ с общим числом 39.0 треугольных поверхностей, как показано на рис. 10. Диапазон влияния шпуров, определяемый каждой шпуром и связанным с ним треугольником, показан на рис. 11.
Изображение полного размера
Рисунок 11
Диапазон воздействия взрывной скважины.
Изображение в натуральную величину
Расчет влияющего объекта шпура в зоне взрыва
Пересечение полигона влияния каждой шпура и трехмерного массива горной породы в зоне взрыва используется для получения столба породы влияния твердое тело каждой взрывной скважины, как показано на рис.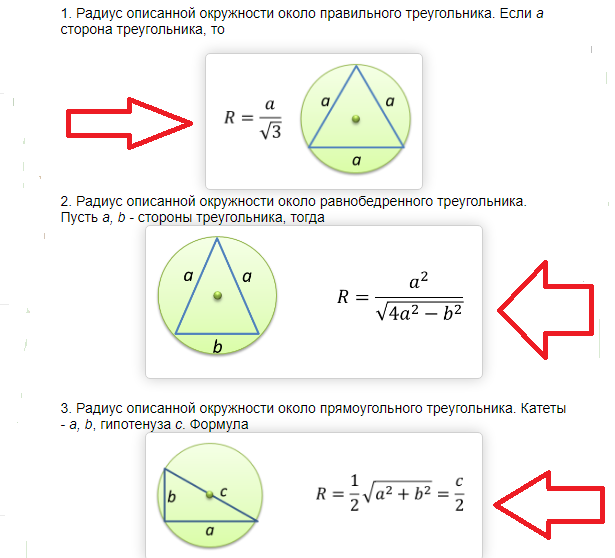 12a,b, представляет собой влияние твердого тела столба породы взрывной скважины ZK2032, размер которого был увеличен пропорционально.
12a,b, представляет собой влияние твердого тела столба породы взрывной скважины ZK2032, размер которого был увеличен пропорционально.
Рисунок 12
Объект скального массива, затронутый взрывной скважиной: ( a ) объект скального массива, влияющий на все взрывные скважины; ( b ) влияние каменной колонны взрывной скважины ZK2032.
Увеличить
Рассчитать количество шпурового заряда зоны взрыва
При расчете количества взрывчатого вещества, необходимого для каждого твердого взрыва, согласно формуле (3), количество взрывчатого вещества, необходимое для каждой пораженной твердой единицы шпура, равно рассчитано с учетом расхода взрывчатого вещества, необходимого для различной литологии. Сумма взрывчатого вещества, необходимого для каждого твердого тела, представляет собой количество взрывчатого вещества, необходимое для каждой трехмерной твердотельной модели взрывной скважины.
Возьмите скважину ZK2032 в качестве примера для расчета количества заряда скважины. Количество заряда рассчитывается в соответствии с объемом каждой единицы объекта и расходом взрывчатого вещества на единицу, требуемым различной литологией. Объем и литология комплексных единиц скважины ZK2032 представлены в таблице 5. Всего имеется 260 твердых единиц, общим объемом 1244,521 м 3 , таким образом, итоговое количество заряда ZK2032 составляет 214,275 кг.
Количество заряда рассчитывается в соответствии с объемом каждой единицы объекта и расходом взрывчатого вещества на единицу, требуемым различной литологией. Объем и литология комплексных единиц скважины ZK2032 представлены в таблице 5. Всего имеется 260 твердых единиц, общим объемом 1244,521 м 3 , таким образом, итоговое количество заряда ZK2032 составляет 214,275 кг.
Таблица 5 Расчет количества заряда шпура ZK2032.
Полноразмерная таблица
Путем расчета количества взрывчатого вещества, необходимого для каждой единицы затронутого объекта в трехмерной модели массива горных пород каждой скважины, получается количество взрывчатого вещества, необходимое для каждой скважины, как показано в Таблице 6. После расчета общий заряд буровой скважины составляет 22 849,147 кг, что на 4,59 % ниже расчетного по петрологии одиночной скважины. Результаты показывают, что заряд шпура, рассчитанный по трехмерной твердотельной модели взрывания горной массы, позволяет эффективно снизить стоимость взрывных работ и повысить эффективность взрывных работ.
Таблица 6 Объем взрывных работ Расчет 3D модели.
Полноразмерная таблица
Приведенный выше пример создания трехмерной твердотельной модели взрываемой горной массы реализован Visual C++ 2012 в деталях следующим образом:
-
1.
Операция доступа к базе данных.
Режим ADO используется для подключения базы данных доступа для реализации операции базы данных взрывных скважин.
-
2.
Создание и визуализация трехмерной твердотельной модели взрываемой горной массы.
Программирование на C++ используется для реализации литологической интерполяции кубического примитива, а многоугольник зоны взрывных работ и треугольная сетка поверхности забоя последовательно используются для разрезания взрываемой горной массы в трехмерную твердотельную модель. AutoCAD 2016 переработан на основе ObjectARX 2016, а класс AcDbSolid используется для визуализации трехмерной твердотельной модели взрываемого горного массива.
AutoCAD 2016 переработан на основе ObjectARX 2016, а класс AcDbSolid используется для визуализации трехмерной твердотельной модели взрываемого горного массива.
При использовании трехмерной твердотельной модели взрываемой горной массы при расчете количества заряда взрывной скважины литология трехмерного твердого тела может быть принята для расчета более точного количества заряда взрывной скважины. Таким образом, точность количества заряда взрывной скважины и эффект взрыва улучшаются.
Обсуждение
В настоящее время литология карьерных перфорационных взрывов в основном получается на основе разведочных скважин. Из-за большой плотности распределения и большого расстояния между разведочными скважинами литология участка взрываемой горной массы не может быть получена точно. Литология одиночной скважины обычно используется для расчета заряда шпура.
Путем сравнения заряда шпура, рассчитанного с помощью петрологии одиночной скважины, с зарядом, рассчитанным с помощью трехмерной модели горной массы шпура, получены результаты, показанные в Таблице 7. Из сравнения видно, что заряд, рассчитанный на основе трехмерной твердотельной модели взрыва горной массы, на 4,59% ниже, чем рассчитанный на основе свойств породы с одной скважиной.
Из сравнения видно, что заряд, рассчитанный на основе трехмерной твердотельной модели взрыва горной массы, на 4,59% ниже, чем рассчитанный на основе свойств породы с одной скважиной.
Таблица 7 Сравнение взрывных зарядов.
Полноразмерный стол
Вывод
На основе данных распознавания горных пород интеллектуальной буровой установки реализован расчет и применение объема заряда шпура на основе трехмерной твердотельной модели взрываемой горной массы, и сделаны следующие выводы:
-
1.
Создать базу данных взрывных скважин для хранения и управления данными интеллектуальной идентификации литологии;
-
2.
Возьмите данные литологии взрывной скважины в качестве образца, примените метод обратных квадратов расстояния для интерполяции твердых элементов в зоне взрывных работ, а затем используйте многоугольник диапазона взрывных работ и сетку треугольника забоя для вырезания трехмерной твердотельной модели взрывных работ.
 горная масса;
горная масса; -
3.
В соответствии с установленной трехмерной твердотельной моделью, с помощью метода расчета заряда шпура, описанного в этой статье, получают диапазон влияния шпура и твердые элементы влияния шпура, а также рассчитывают заряд шпура. Результат заряда сравнивается с зарядом, рассчитанным методом одной скважины, и стоимость уменьшается на 4,59.%;
Все процессы расчета количества шпурового заряда на основе трехмерной твердотельной модели взрываемой горной массы реализованы с помощью программирования на языке C++. Расчет фактического количества горной массы при взрывных работах выполнен на примере угольной шахты Xilinhot Shengli во Внутренней Монголии, что указывает на то, что это полезно для предприятия в повышении эффективности взрывных работ и снижении производственных затрат на взрывные работы.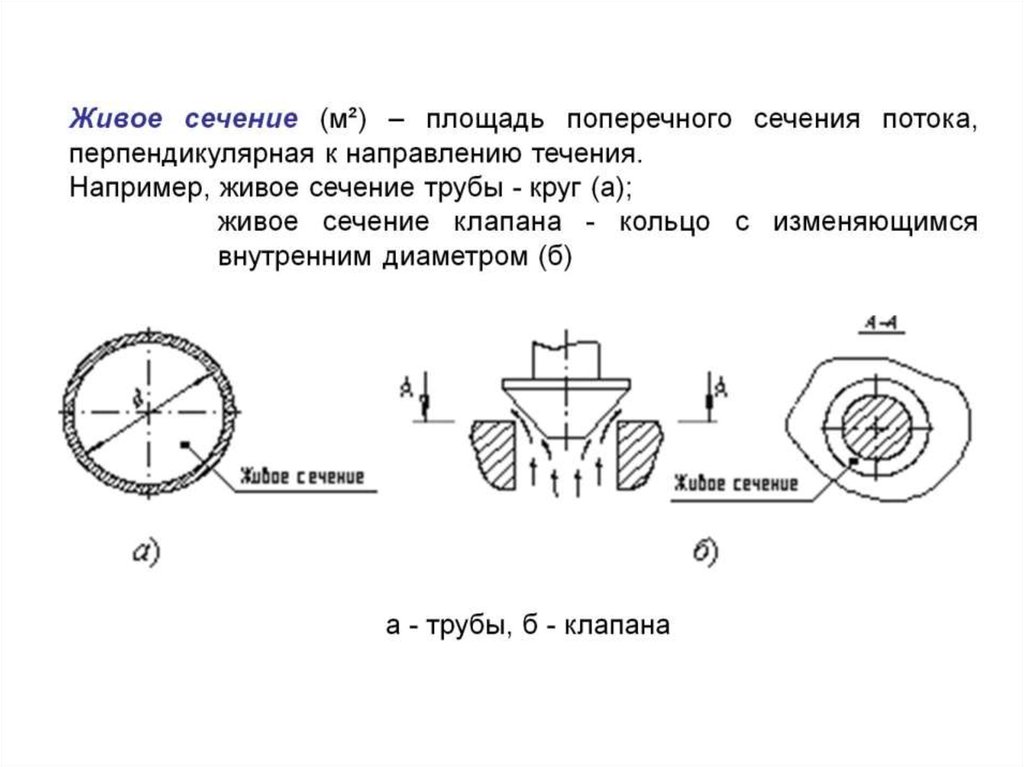 В данной статье рассматривается только расчет шпурового заряда. На следующем этапе трехмерная твердотельная модель взрываемой горной массы может быть использована для оптимизации расчета других параметров взрывных работ.
В данной статье рассматривается только расчет шпурового заряда. На следующем этапе трехмерная твердотельная модель взрываемой горной массы может быть использована для оптимизации расчета других параметров взрывных работ.
Ссылки
-
Li, G., Qiao, Y., Zheng, Y., Li, Y. & Wu, W. Полуконтролируемое обучение на основе генеративной состязательной сети и ее применение для распознавания литологии. IEEE Access 7 , 67428–67437 (2019 г.).
Артикул
Google ученый -
Саху, С. и Джха, М. К. Распознавание образов в литологической классификации: моделирование с использованием нейронных сетей, самоорганизующихся карт и генетических алгоритмов. Гидрогеол. J. 25 (2), 311–330 (2017).
ОБЪЯВЛЕНИЕ
Статья
Google ученый -
Сантос, Р.
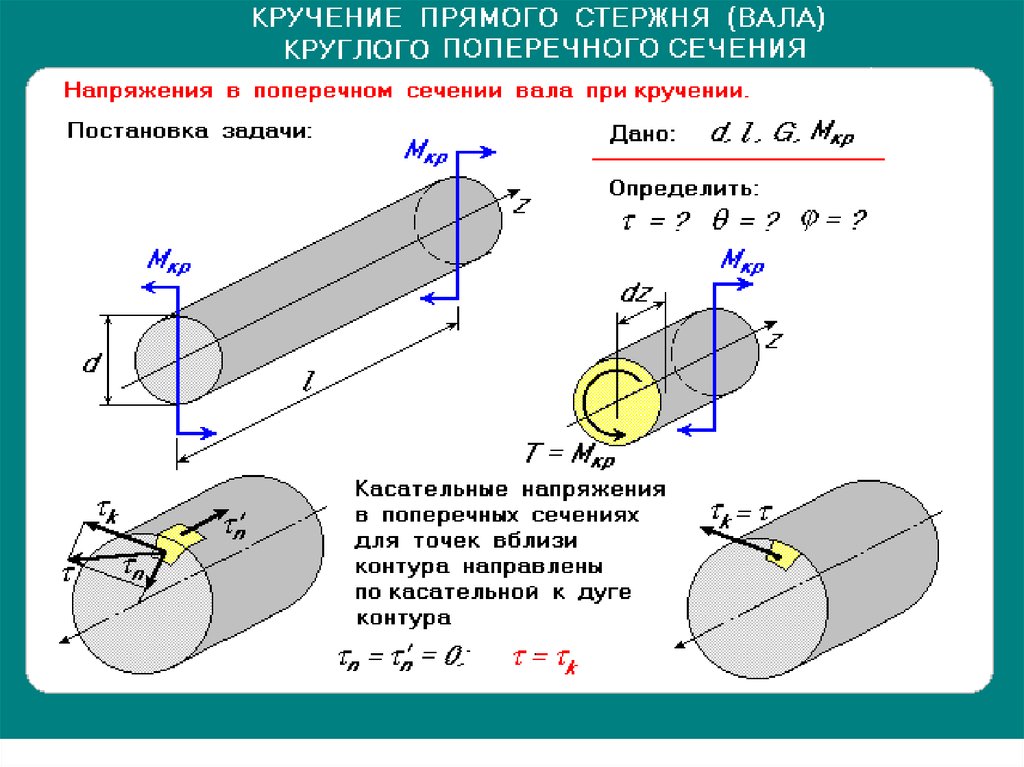 В. Д., Артола, Ф., Фонтура, С. Д. и Велласко, М. Распознавание литологии ансамблями нейронных сетей. Конспект лекций по информатике (2002).
В. Д., Артола, Ф., Фонтура, С. Д. и Велласко, М. Распознавание литологии ансамблями нейронных сетей. Конспект лекций по информатике (2002). -
Чен, К. и Шао, Ю. Применение усовершенствованного алгоритма нейронной сети bp для прогнозирования качества воздуха в городах: данные из Китая. Документ, представленный на семинаре по вычислительному интеллекту и промышленному применению (2008 г.).
-
Чжан Ю. и Пан Б. З. Применение метода нейронной сети SOM для распознавания вулканической литологии на основе анализа основных компонентов. Технология ГИС (2009).
-
Сунь, Л., Вэй, Ю., Цай, Х., Ян, Дж. и Сяо, Дж. Усовершенствованный алгоритм быстрой адаптивной интерполяции IDW, основанный на характеристике выборки скважинных данных и ее применении. J. Phys. конф. сер. 1284 , 012074 (2019).
Артикул
Google ученый -
Лю, Х., Чен, С., Хоу, М. и Хе, Л. Усовершенствованное применение метода обратного взвешивания по расстоянию с учетом пространственной автокорреляции в трехмерном геологическом моделировании. Науки о Земле. Инф. https://doi.org/10.1007/s12145-019-00436-6 (2019).
Артикул
Google ученый -
Цзя, К., Че, Д. и Ли, В. Моделирование эффективной поверхности угольного пласта с помощью усовершенствованного многомасштабного метода интерполяции на основе анизотропии. Вычисл. Geosci. 124 , 72–84 (2019).
ОБЪЯВЛЕНИЕ
Статья
Google ученый -
Marshallinger, R., Jandrisevits, C. & Zobl, F. Визуальная программа LISP для вокселизации твердотельных моделей AutoCAD. Вычисл. Geosci. 74 , 110–120 (2015).
ОБЪЯВЛЕНИЕ
Статья
Google ученый -
Пинг, Л. И., Ван, Ю. Дж. и Бо, К. Э. Теоретический расчет глубины взрывной скважины и длины под нагрузкой при прогрессивной спиральной резке. Взрывные работы (2012 г.).
-
Ван Ю. Ф. Расчет параметров буровзрывных работ на поверхности золотого рудника Пайшаньлоу в Ляонине. Архитектура Шаньси (2007 г.).
-
Шим, Х.-Дж., Рю, Д.-В., Чанг, С.-К., Синн, Дж.-Х. и Сонг, Ж.-Ж. Оптимизированный дизайн взрывных работ для крупномасштабных карьеров на основе трехмерного пространственного распределения фактора породы. Междунар. Дж. Рок Мех. Мин. науч. 46 (2), 326–332 (2009).
Артикул
Google ученый -
Перссон, П.А. Взрывные работы и взрывчатые вещества. Междунар. Дж. Рок Мех. Мин. науч. геомех. Абстр. 6 , 278А (1994).
Google ученый
-
Ву К., Чжушань Шао Су., Цинь Н.З. и Хункунь Ху. Аналитическая оценка влияния высокодеформируемых элементов на обделку тоннеля в вязкоупругих горных породах.
 Междунар. Дж. Заявл. мех. 12 (03), 2050030 (2020).
Междунар. Дж. Заявл. мех. 12 (03), 2050030 (2020). Артикул
Google ученый -
Ву, К., Шао, З., Цинь, С., Вэй, В. и Чу, З. Критический обзор характеристик податливых опор в продавливаемых туннелях. Тунн. Подгр. Космическая техника. 115 , 103815 (2021).
Артикул
Google ученый -
Алтити, А. Х., Альравашде, Р. О. и Альнавафлех, Х. М. Открытые горные работы: методы добычи — прошлое, настоящее и будущее (2021 г.).
-
Лак, М., Фатехи Марджи, М., Ярахамди Бафги, А. Р. и Абдоллахипур, А. Дискретно-элементное моделирование расширения трещин, вызванных взрывом, в сочлененных массивах горных пород. Дж Мин. Окружающая среда. 10 (1), 125–138 (2019).
Google ученый
-
Лак, М.
 , Фатехи Марджи, М., Ярахмади Бафги, А. и Абдоллахипур, А. Аналитическое и численное моделирование горно-взрывных работ с использованием двумерной упруго-динамической функции Грина. Междунар. Дж. Рок Мех. Мин. науч. 114 , 208–217 (2019).
, Фатехи Марджи, М., Ярахмади Бафги, А. и Абдоллахипур, А. Аналитическое и численное моделирование горно-взрывных работ с использованием двумерной упруго-динамической функции Грина. Междунар. Дж. Рок Мех. Мин. науч. 114 , 208–217 (2019). Артикул
Google ученый -
Калбусси, Н., Рапапорт, А., Байен, Т., Амар, Н. и Бен, Э. Связанный метод конечных разностей и граничных элементов для моделирования распространения вызванных взрывом радиальных трещин вокруг ствола скважины. IEEE Trans. автомат. Контроль 5 (2019).
-
Марджи, М.Ф. Моделирование трещин в фрагментации горных пород с помощью метода разрыва смещения более высокого порядка (1996).
-
Цуй, К., Чжан, З. и Сяо, X. Технология САПР при производстве взрывных работ на карьере — чертеж профиля взрывной скважины и расчет заряда. Взрыв 03 , 18–19 (1987).

Google ученый
-
Арнольд Д. Н., Мукерджи А. и Пули Л. Адаптированные к местным условиям тетраэдрические сетки с использованием деления пополам. SIAM J. Sci. вычисл. 22 (2), 431–448 (2000).
MathSciNet
Статья
Google ученый -
Li, X., Shephard, M.S. & Beall, M.W. Адаптация трехмерной анизотропной сетки путем модификации сетки. Вычисл. Методы Прил. мех. англ. 194 (48), 4915–4950 (2005).
ОБЪЯВЛЕНИЕ
MathSciNet
Статья
Google ученый -
Нго, Л. К. и Чой, Х. Г. Многоуровневый адаптивный метод уточнения сетки для моделирования многофазного потока на неструктурированных сетках. Междунар. Дж. Нумер. Методы инж. 110 (10), 947–971 (2017).
-
Окереке, М.
 и Китс, С. Генерация сетки конечных элементов. Springer Tracts in Machine Engineering (CRC, Париж, 2018 г.).
и Китс, С. Генерация сетки конечных элементов. Springer Tracts in Machine Engineering (CRC, Париж, 2018 г.). МАТЕМАТИКА
Google ученый -
Сунь, Лу., Чжао, Г. и Ма, X. Методы адаптивной генерации и локального уточнения трехмерной шестигранной сетки элементов. Конечный элемент. Анальный. Дес. 50 , 184–200 (2012).
MathSciNet
Статья
Google ученый -
Ван, Б., Мэй, Г. и Сюй, Н. Метод создания высококачественных тетраэдрических сеток геологических моделей с использованием Cgal. MethodsX 7 , 101061 (2020).
Артикул
Google ученый -
Ю, Ю. Х., Коу, X. Ю. и Тан, С. Т. Создание адаптивной тетраэдрической сетки трехмерных гетерогенных объектов. Вычисл. Приложение для автоматизированного проектирования.
 12 (5), 580–588 (2015).
12 (5), 580–588 (2015). Артикул
Google ученый -
Зенер, Б., Бернер, Дж. Х., Гёрц, И. и Спитцер, К. Рабочие процессы для создания тетраэдрических сеток для конечно-элементного моделирования сложных геологических структур. Вычисл. Geosci. 79 , 105–117 (2015).
ОБЪЯВЛЕНИЕ
Статья
Google ученый -
Бо, Ф. и др. Сравнение трехмерного геологического моделирования на основе двух алгоритмов интерполяции. J. Jilin Univ. (Науки о Земле. Ред.) 49 (04), 120008 (2019).
Google ученый
-
Модис, К., Ставру, С., Терезопулос, Н. и Ваттис, Д. Геостатистика по сравнению с обратными квадратами расстояний в оценке рудных запасов: Сравнительный пример медного рудного тела на Кипре. Мин. Технол.
 117 (1), 48–52 (2008).
117 (1), 48–52 (2008). Артикул
Google ученый -
Циммерман Д., Павлик К., Рагглс А. и Армстронг М.П. Экспериментальное сравнение обычного и универсального кригинга и взвешивания методом обратного расстояния. Матем. геол. 31 (4), 375–390 (1999).
Артикул
Google ученый -
Лу, Г.Ю. и Вонг, Д.В. Адаптивный метод пространственной интерполяции с взвешиванием по обратному расстоянию. Вычисл. Geosci. 34 (9), 1044–1055 (2008).
ОБЪЯВЛЕНИЕ
Статья
Google ученый -
Gotway, C. A., Ferguson, R. B., Hergert, G. W. & Peterson, T. A. Сравнение кригинга и методов обратного расстояния для картирования параметров почвы. Почвоведение. соц. Являюсь. J. 60 (4), 1237–1247 (1996).
ОБЪЯВЛЕНИЕ
КАС
Статья
Google ученый -
Чжоу, Л., Ван, Х., Лу, X., Чжан, В. и Чжан, X. Алгоритм создания сетки криволинейной поверхности на основе уточнения Делоне. Междунар. J. Распознавание образов. Артиф. Интел. 34 , 2050007 (2019).
Артикул
Google ученый -
Si, H. Анализ алгоритма уточнения Делоне Шевчука. В Материалы 18-го Международного круглого стола по созданию сетки , 499–518 (Springer, 2009).
Ссылки для скачивания
Анализ наконечников | MechaniCalc
Калькулятор
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Пожалуйста, включите JavaScript.
Проушина, также известная как подъемная проушина или проушина, представляет собой пластину с отверстием, размер которого соответствует размеру штифта с плоской головкой. Наконечники используются в сочетании со шпильками для передачи нагрузки между различными механическими компонентами. Общие области применения, в которых используются наконечники, включают:
- укрепленные спинки с проушинами, поднимаемые скобами и другим такелажем
- соединения между приводами и другими конструкциями (например, цапфовое соединение, шарнирное соединение)
- дверные петли
Преимущества наконечников перед другими типами соединений, которые используются для передачи нагрузки, включают:
- возможно вращение между компонентами
- быстрая и простая установка
Содержание
Обзор анализа выступов
Анализ выступа обманчиво сложен, поскольку существует несколько одновременных взаимодействующих режимов отказа.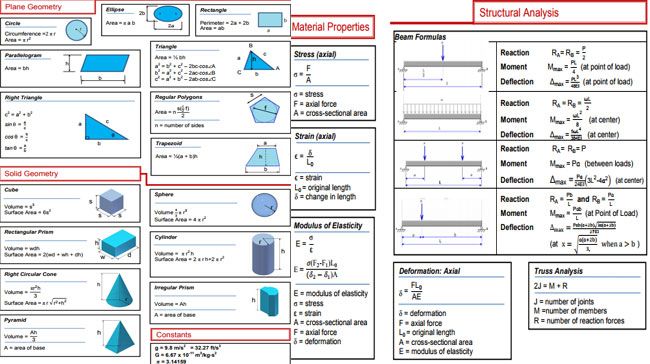 Эти виды отказов связаны с различными областями выступа, как показано на рисунке ниже (Примечание: рисунок не в масштабе):
Эти виды отказов связаны с различными областями выступа, как показано на рисунке ниже (Примечание: рисунок не в масштабе):
Виды отказов наконечника перечислены ниже. Номера соответствуют помеченным участкам на рисунке выше:
- Разрушение натяжения в сетке
- Разрушение при сдвиге по двум плоскостям
- Выход из строя подшипника
- Разрушение кольцевого натяжения / перелом в одной плоскости
- Выпучивание вне плоскости («выпуклость») — (на рисунке не показано)
Существует несколько распространенных методов анализа ушка:
- Упрощенный анализ. Этот метод основан на первых принципах и включает в себя упрощение предположений о характере отказа и расчет коэффициентов безопасности. Преимущество этого заключается в том, что он относительно прост, но дает лишь приблизительное определение адекватности проушины.
-
Метод ВВС. Этот метод учитывает большинство описанных выше видов отказов и использует эмпирические кривые для более точного определения допустимых нагрузок.
 Этот метод позволяет использовать проушины при осевой нагрузке, поперечной нагрузке или наклонной нагрузке. Этот метод также учитывает взаимодействие между выступом и штифтом.
Этот метод позволяет использовать проушины при осевой нагрузке, поперечной нагрузке или наклонной нагрузке. Этот метод также учитывает взаимодействие между выступом и штифтом.
- ASME BTH — этот метод учитывает большинство описанных выше режимов отказа и использует упрощенные уравнения с поправочными коэффициентами, основанными на эмпирических данных, для более точного определения допустимых нагрузок. Этот метод проще, чем метод Air Force, но он позволяет использовать проушины только при осевой нагрузке и не учитывает взаимодействие между проушиной и штифтом с плоской головкой.
Все эти методы описаны в следующих разделах.
Упрощенный анализ
Этот метод основан на первых принципах (а также на упрощенном методе, изложенном Брюном) и включает в себя упрощающие предположения о характере отказа. Хотя его относительно легко выполнить, он дает лишь приблизительное определение адекватности выступа и не должен использоваться для критических конструкций.
В упрощенном анализе рассматриваются следующие виды отказов:
- Разрыв натяжения в секции сетки
- Разрушение при сдвиге по двум плоскостям
- Выход из строя подшипника
Коэффициент безопасности рассчитывается для каждого из режимов отказа, и, если каждый фактор безопасности является приемлемым, можно считать, что проушина прошла успешно. На рисунке ниже выступ показан синим цветом, а штифт зеленым.
Размеры на рисунке такие:
- D h = диаметр отверстия
- D p = диаметр штифта
- R = краевое расстояние (расстояние от центра отверстия до края выступа в направлении приложенной нагрузки)
- r = радиус кривизны кромки выступа (больше или равен R)
- a = расстояние от края отверстия до края выступа = R − 0,5 D h
- ш = ширина
- t = толщина (на рисунке не показана — толщина указана на странице)
- Z = потеря длины плоскости сдвига из-за кривизны на конце выступа
- ϕ = угол установки плоскости сдвига = 40°
Нужен калькулятор люфта?
Попробуйте наш калькулятор тяги, основанный на методологии, описанной здесь.
- Допускает осевую, поперечную или наклонную нагрузку
- Выполнение расчетов прочности выступов, прочности штифтов и прочности соединения при двойном сдвиге
Ошибка натяжения в секции сетки
Разрушение натяжения в секции сетки происходит в поперечном сечении, выделенном красным на рисунке ниже:
Площадь сечения сетки определяется по формуле:
A t = (w − D h ) t
Предельная растягивающая нагрузка — это нагрузка, которая может привести к разрушению при растяжении по всей сетке, и определяется по формуле:
P ту = S ту А т
где S tu — предел прочности при растяжении материала наконечника. В приведенном выше уравнении предполагается равномерное растягивающее напряжение по поперечному сечению. В действительности будет концентрация напряжения из-за потока напряжения вокруг отверстия.
Коэффициент безопасности определяется:
Срез-вырыв вдоль двух плоскостей
Вырыв при сдвиге происходит по двум плоскостям сдвига, выделенным красным цветом на рисунке ниже:
Общая площадь плоскости сдвига определяется по формуле:
A s = 2 л sp t
где L sp — длина плоскости сдвига, t — толщина выступа. Простой и консервативный подход состоит в том, чтобы рассчитать длину одной плоскости сдвига как:
Простой и консервативный подход состоит в том, чтобы рассчитать длину одной плоскости сдвига как:
L sp = а
где a = R − 0,5 D h , как показано на рисунке выше. Если желательно учесть немного более длинную плоскость сдвига, обычно рассматривают линию под углом 40 градусов, проходящую от центра срезного штифта. В точке, где эта линия под углом 40 градусов пересекает отверстие для штифта, продлите плоскость сдвига горизонтально до внешнего края выступа. В этом случае L sp рассчитывается как:
где ϕ представляет собой угол расположения плоскости сдвига, равный 40°, а Z представляет собой потерю длины плоскости сдвига из-за кривизны на конце выступа. Эта потеря рассчитывается как:
Обратите внимание, что если конец выступа плоский, то r равно бесконечности, а Z равно нулю.
Предельная сдвигающая нагрузка — это нагрузка, которая может привести к разрыву при сдвиге в двух плоскостях, и определяется по формуле:
P вс = S вс А с
где S su — предел прочности на сдвиг материала проушины.
Коэффициент безопасности определяется:
Выход из строя подшипника
Подшипник возникает между поверхностью штифта и внутренней поверхностью отверстия в выступе, как показано на рисунке ниже:
Площадь опоры определяется по формуле:
А бр = Д р т
Обратите внимание, что поскольку длина опорной поверхности равна диаметру штифта, а длина окружности определяется как C = πD, то:
- длина опорной поверхности также равна 1/π, умноженной на длину окружности штифта.
- угол наклона опорной поверхности равен 2 радианам &приблизительно; 115°
Предельная нагрузка на подшипник — это нагрузка, которая может привести к выходу из строя подшипника, и определяется по формуле:
P Брю = S Брю A Брю
где S bru — минимум предела прочности на смятие материала проушины и предела прочности на смятие материала штифта. Предел прочности на смятие можно приблизительно оценить как 1,5·S вт .
Коэффициент безопасности определяется:
Если в проушину запрессована втулка, то подшипник необходимо рассчитывать для обеих групп контакта:
- Штифт на втулке
- Втулка на выступе
Подпишитесь, чтобы время от времени получать обновления о последних улучшениях:
Метод ВВС
Метод анализа выступов ВВС широко используется в промышленности и задокументирован в Руководстве по анализу напряжений Лаборатории динамики полета ВВС (FDL). Этот метод тесно связан с методами, представленными в Melcon & Hoblit и Bruhn, и в значительной степени опирается на кривые, полученные на основе эмпирических данных. Хотя этот метод несколько более сложен, чем другие методы анализа проушины, он невероятно полезен, поскольку позволяет учитывать проушины при осевой, поперечной или наклонной нагрузке, а также потому, что он учитывает взаимодействие между проушиной и штифтом.
Ознакомьтесь с нашим калькулятором выступов, основанным на методе Air Force, описанном здесь.
В этом разделе осевая нагрузка, поперечная нагрузка и наклонная нагрузка обсуждаются отдельно. В этих разделах не учитывается влияние штифта на прочность выступа. Обсуждение взаимодействия штифта и выступа дано в конце.
Осевая нагрузка
Для проушин с осевой нагрузкой метод Air Force оценивает проушину на предмет разрушения подшипника, разрушения при сдвиге, разрушения при кольцевом натяжении и разрушения по сетке. Три режима отказа фактически объединены в один режим отказа — «несущая способность» учитывает несущую способность, срез и кольцевое растяжение. Это согласуется с Bruhn и Melcon & Hoblit.
Интересующие размеры проушины с осевой нагрузкой показаны на рисунке ниже:
Размеры на рисунке включают:
- D = диаметр отверстия
- D p = диаметр штифта
- e = краевое расстояние
- a = расстояние от края отверстия до края выступа = e − 0,5 D
- ш = ширина
- т = толщина
Несущая способность при осевой нагрузке
Предельная нагрузка на подшипник, учитывающая подшипник, срез и кольцевое натяжение, определяется по формуле:
где D — диаметр отверстия, t — толщина проушины, а S tu и S ty — предел прочности материала проушины и предел текучести при растяжении соответственно. F bru.L и F bry.L представляют собой предельные напряжения при проушинах и предел текучести при смятии, соответственно, и определяются следующими уравнениями:
F bru.L и F bry.L представляют собой предельные напряжения при проушинах и предел текучести при смятии, соответственно, и определяются следующими уравнениями:
| e/D < 1,5 | e/D ≥ 1,5 | |
|---|---|---|
| Предельная нагрузка на подшипник, F br.L : | К С ту | |
| Предел текучести, F bry.L : | К С ти |
Уравнение для предельной нагрузки на подшипник можно свести к следующему:
При отношении e/D менее 1,5 отверстие расположено близко к краю выступа, поэтому срез и кольцевое растяжение, вероятно, будут наиболее критическими видами разрушения. При больших значениях e/D отверстие расположено дальше от края, и поэтому подшипник, вероятно, будет критическим видом отказа.
Коэффициент K в приведенных выше уравнениях представляет собой допустимый коэффициент осевой нагрузки , который учитывает эффекты взаимодействия между различными видами разрушения (подшипник, срез и кольцевое растяжение). Значение K считывается с одного из следующих двух графиков. Первый график используется для D/t ≤ 5, что является наиболее распространенным случаем. Если D/t > 5, то выступ тонкий, и в этом случае значение K считывается со второго графика ниже. (Примечание 2)
Значение K считывается с одного из следующих двух графиков. Первый график используется для D/t ≤ 5, что является наиболее распространенным случаем. Если D/t > 5, то выступ тонкий, и в этом случае значение K считывается со второго графика ниже. (Примечание 2)
Прочность подшипника втулки при осевой нагрузке
Если в проушине имеется втулка, то необходимо рассчитать несущую способность втулки. Предельная нагрузка на втулку определяется по формуле:
P u.B = 1.304 S cy.B D p t
где D p — диаметр штифта, t — толщина втулки (принимается равной толщине выступа), а S cy.B — предел текучести материала втулки при сжатии. В руководстве ВВС предполагается, что предел прочности при сжатии материала втулки S 9.0139 cu.B , равным 1,304·S cy.B .
Если втулки в проушине нет, то расчет все равно следует выполнять, принимая, что материалом проушины является материал втулки.
Прочность сечения сетки при осевой нагрузке
Предельная нагрузка на секцию нетто учитывает отказ от растяжения по секции сетки и рассчитывается по формуле:
где w — ширина, а D — диаметр отверстия. Ф nu.L и F ny.L представляют собой предельное напряжение и напряжение текучести в поперечном сечении, соответственно, и определяются следующими уравнениями:
| Предельное напряжение сечения сетки: | F ну.L = K n S ту |
| Предел текучести Напряжение нетто-сечения: | F ny.L = K n S ty |
Уравнение для расчетной предельной нагрузки сечения можно свести к следующему:
P nu.L = K n · min(S tu , 1.304 S ty ) · (w − D) · t
Коэффициент K n в уравнениях, приведенных выше, представляет собой чистый коэффициент напряжения растяжения , который представляет собой предельное значение допустимых напряжений.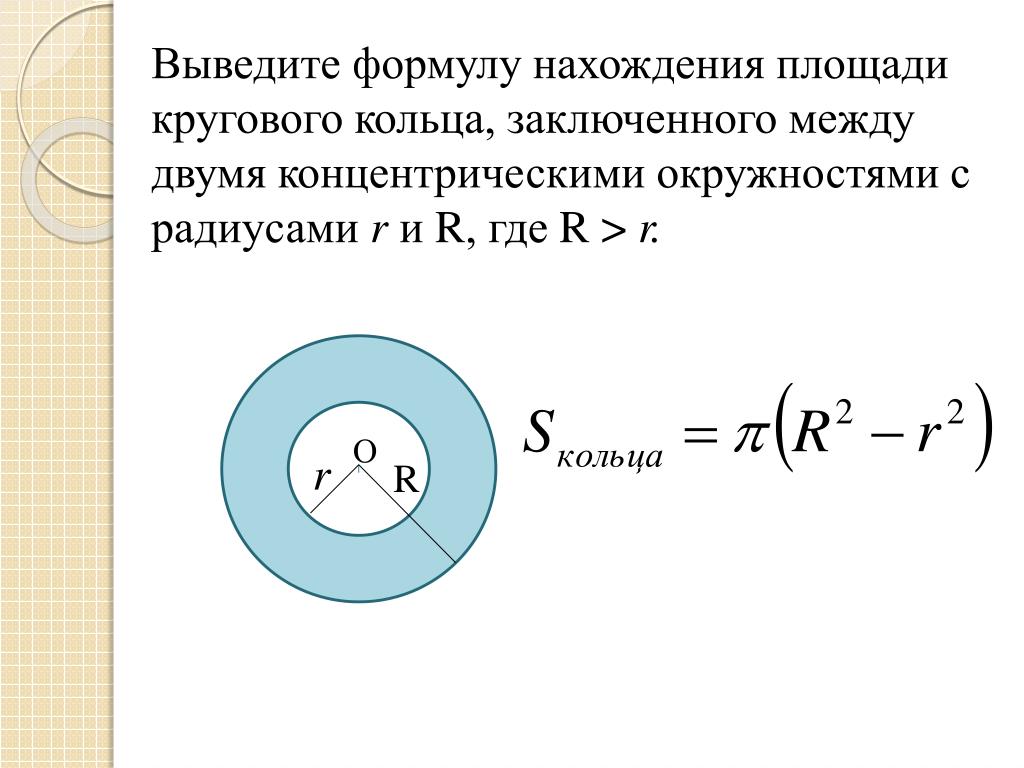 Значение K n определяется путем интерполяции между следующими графиками:
Значение K n определяется путем интерполяции между следующими графиками:
На приведенных выше кривых F ty и F tu — предел текучести и предел прочности материала соответственно, E — модуль упругости, а ε u — предельная деформация (т. е. полная деформация при разрушении).
Расчетная прочность при осевой нагрузке
Расчетная предельная нагрузка для проушины, нагруженной в осевом направлении, представляет собой минимум предельной нагрузки на подшипник, предельной нагрузки на втулку и предельной нагрузки на сечение нетто:
P u.L.B = min( P bru.L , P u.B , P nu.L )
Поперечная нагрузка
Расчет поперечной нагрузки аналогичен анализу осевой нагрузки. Однако вид разрушения при поперечной нагрузке более сложен, чем при осевой нагрузке, и разные размеры имеют решающее значение для определения прочности проушин. Интересующие размеры проушины с поперечной нагрузкой показаны на рисунке ниже:
где h 1 , h 2 , h 3 и h 4 представляют интересующие плоскости отказа.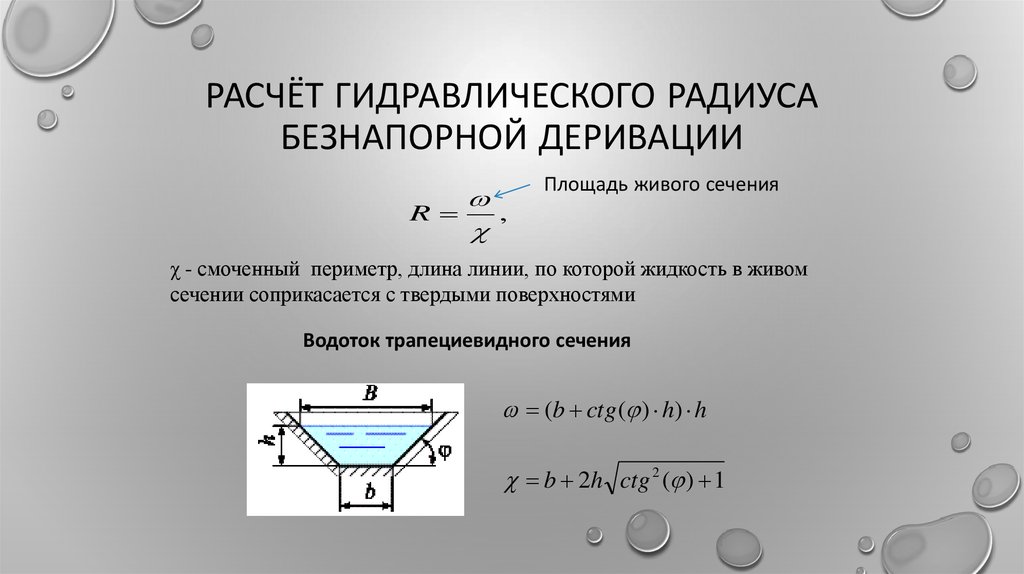 Если проушина симметрична, то значения этих размеров можно легко получить из размеров проушины, нагруженной в осевом направлении:
Если проушина симметрична, то значения этих размеров можно легко получить из размеров проушины, нагруженной в осевом направлении:
| h 2 = 0,5 (w − D) |
| h 1 = h 4 = h 2 + плюс; 0,5 D (1 − cos 45°) |
| h 3 = a |
Следует отметить, что h 3 определяется как наименьший размер на любом радиальном сечении вокруг отверстия, но обычно он равен a. Из приведенных выше размеров рассчитывается эффективное краевое расстояние :
Приведенное выше уравнение представляет собой просто «обратное среднее», которое придает больший вес размеру h 1 , поскольку на эту секцию приходится большая часть нагрузки. (Примечание 3)
Прочность проушин при поперечной нагрузке
Предельная поперечная нагрузка определяется по формуле:
где D — диаметр отверстия, t — толщина выступа. F bru. L и F bry.L представляют собой предельные напряжения при проушинах и предел текучести при смятии, соответственно, и определяются следующими уравнениями:
L и F bry.L представляют собой предельные напряжения при проушинах и предел текучести при смятии, соответственно, и определяются следующими уравнениями:
| Предельное напряжение подшипника: | F брю.L = K правда S ту |
| Предел текучести Напряжение подшипника: | F бр.L = K попроб. S ty |
где K tru и K try — коэффициенты поперечной предельной и текучей нагрузки, определяемые по следующему графику:
Несущая способность втулки при поперечной нагрузке
Несущая способность втулки в проушине с поперечной нагрузкой такая же, как и у проушины с осевой нагрузкой:
Р тру.Б = Р у.Б
где P u.B — прочность на смятие втулки при осевой нагрузке проушины.
Расчетная прочность при поперечной нагрузке
Расчетная предельная нагрузка для проушины с поперечной нагрузкой равна минимальной предельной нагрузке на проушину и предельной нагрузке на втулку:
P tr. L.B = min( P tr.L , P tr.B )
L.B = min( P tr.L , P tr.B )
Нужен калькулятор люфта?
Попробуйте наш калькулятор тяги, основанный на методологии, описанной здесь.
- Допускает осевую, поперечную или наклонную нагрузку
- Выполнение расчетов прочности выступов, прочности штифтов и прочности соединения при двойном сдвиге
Наклонная нагрузка
В проушине с наклонной нагрузкой приложенная нагрузка имеет как осевую, так и поперечную составляющие, как показано на рисунке ниже:
Для проушины с наклонной нагрузкой приложенная нагрузка должна быть разбита на осевую и поперечную составляющие, P x и P tr , а силы в осевом и поперечном направлениях должны быть рассчитаны, как обсуждалось в предыдущих разделах. Затем можно определить допустимую кривую нагрузки, которая принимает форму уравнения взаимодействия и представлена ниже:
Кривая допустимой нагрузки определяет пределы, при которых проушина, как ожидается, выйдет из строя — она определяет предельную нагрузку для данного сочетания приложенной осевой и поперечной нагрузки. В приведенном выше уравнении P ax.ult — осевая составляющая предельной нагрузки, P tr.ult — поперечная составляющая предельной нагрузки, P u.L.B — расчетная прочность при осевой нагрузке, а P tru.L.B — расчетная прочность при поперечной нагрузке. Кривая допустимой нагрузки показана ниже:
В приведенном выше уравнении P ax.ult — осевая составляющая предельной нагрузки, P tr.ult — поперечная составляющая предельной нагрузки, P u.L.B — расчетная прочность при осевой нагрузке, а P tru.L.B — расчетная прочность при поперечной нагрузке. Кривая допустимой нагрузки показана ниже:
На рисунке выше значения по оси y представляют собой отношения поперечной приложенной нагрузки к поперечной прочности, а значения по оси x представляют собой отношения осевой приложенной нагрузки к осевой прочности.
| Коэффициент осевой нагрузки | Коэффициент поперечной нагрузки |
|---|---|
Должна быть нанесена точка для приложенной нагрузки с координатами (R x , R tr ). Любая точка, попадающая в пределы кривой допустимой нагрузки, имеет коэффициент безопасности ≥ 1 по отношению к предельной нагрузке. Обратите внимание, что если приложенная нагрузка является полностью осевой, то значение для R tr равно 0, а точка (R ax , R tr ) лежит вдоль оси x, поэтому предельная нагрузка представляет собой просто расчетную осевую прочность. То же самое для полностью поперечной приложенной нагрузки; в этом случае точка лежит вдоль оси Y, поэтому предельная нагрузка представляет собой поперечную расчетную прочность.
То же самое для полностью поперечной приложенной нагрузки; в этом случае точка лежит вдоль оси Y, поэтому предельная нагрузка представляет собой поперечную расчетную прочность.
Для приложенной нагрузки как с осевой, так и с поперечной составляющей предельная нагрузка рассчитывается путем проведения линии от начала координат через точку (R ax , R tr ), а затем через кривую допустимой нагрузки. это нагрузочная линия , и она имеет наклон:
Коэффициенты предельной нагрузки определяются пересечением линии нагрузки с кривой допустимой нагрузки. Затем эти предельные отношения можно использовать для расчета значений предельной нагрузки в осевом и поперечном направлениях.
| Коэффициент предельной осевой нагрузки | Коэффициент предельной поперечной нагрузки |
|---|---|
Следует отметить, что уравнение для наклона, приведенное выше, не согласуется с наклоном, указанным в Руководстве ВВС. Обсуждение приведено в приложении.
Обсуждение приведено в приложении.
Вместо того, чтобы определять предельные значения на графике, их можно рассчитать напрямую, отметив, что компоненты предельной нагрузки P ax.ult и P tr.ult связаны соотношением:
P tr.ult = P ax.ult · tan(α)
где α — угол приложенной нагрузки по отношению к осевому направлению. (Примечание 4) Уравнение, определяющее кривую допустимой нагрузки, можно затем решить для предельной осевой нагрузки, заменив приведенное выше соотношение для предельной поперечной нагрузки:
Тогда предельная приложенная нагрузка может быть определена по формуле:
Коэффициент запаса рассчитывается по: (Примечание 5)
Прочность на двойной сдвиг
Важно, чтобы штифт в соединении был достаточно прочным, чтобы равномерно распределять нагрузку по проушинам. Несмотря на то, что слабый штифт на практике обычно не ломается, чрезмерный изгиб штифта приведет к тому, что нагрузка будет «максимально возрастать» вблизи плоскостей сдвига, так что внешние края выступов воспринимают большие нагрузки, а внутренние части выступов относительно выгружен. Это может привести к тому, что материал вокруг отверстий на внешних поверхностях выступов деформируется достаточно сильно, чтобы вызвать разрушение, и выступ выйдет из строя при более низкой нагрузке, чем предполагалось.
Это может привести к тому, что материал вокруг отверстий на внешних поверхностях выступов деформируется достаточно сильно, чтобы вызвать разрушение, и выступ выйдет из строя при более низкой нагрузке, чем предполагалось.
Один эффект, который помогает в этой ситуации, заключается в том, что по мере того, как нагрузка концентрируется вблизи плоскостей сдвига, изгибающее плечо уменьшается, и, следовательно, уменьшается изгибающий момент в штифте. Однако исследование, процитированное Молконом и Хоблитом, показало, что это снижение изгибающего момента «редко превышает 25 процентов, а обычно намного меньше».
Поскольку изгиб штифта влияет на прочность проушины, очень важно учитывать прочность штифта при анализе соединения. В этом разделе представлен метод расчета допустимой нагрузки для соединения с двойным сдвигом. Пример соединения с двойным сдвигом показан ниже:
В соединении с двойным сдвигом есть два внешних (охватывающих) выступа, один внутренний (охватываемый) выступ и штифт.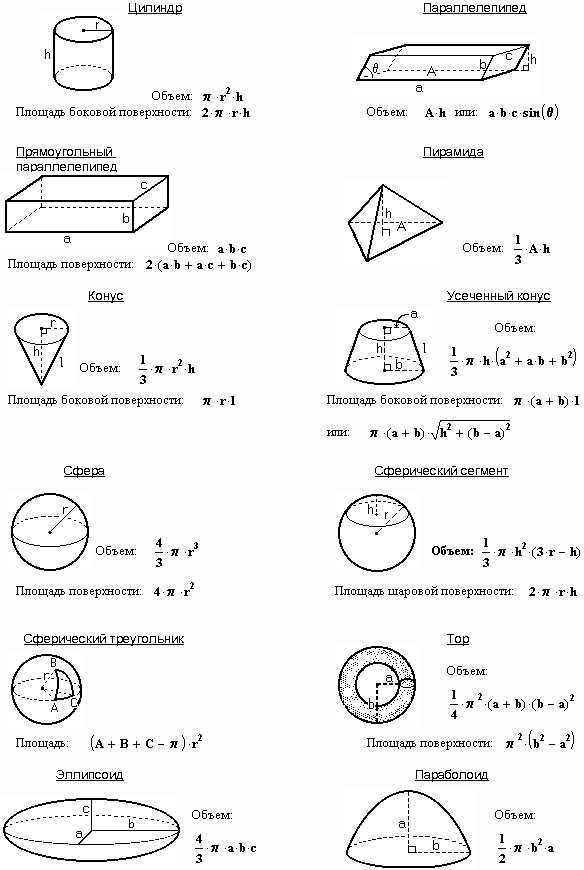
Общий процесс определения допустимой нагрузки показан на диаграмме ниже:
Расчет прочности соединения без учета влияния штифтов
Первоначально игнорируя влияние изгиба штифта, рассчитайте предельную нагрузку каждой проушины в соединении, используя методы, описанные в предыдущих разделах. Затем рассчитайте номинальную предельную нагрузку на соединение (без учета прочности штифта):
P u.J.nom = min( 2·P ульт.F , P ульт.M )
где P ult.M — предельная нагрузка для охватываемой проушины, а P ult.F — предельная нагрузка для одиночной охватывающей проушины. Так как нагрузку поддерживают 2 проушины с внутренней резьбой, предельная нагрузка по отношению к проушинам с внутренней резьбой составляет 2·P ult.F .
Расчет прочности штифта на сдвиг и изгиб
Необходимо рассчитать прочность на сдвиг и прочность на изгиб штифта.
Прочность на сдвиг штифта
Предельная сдвигающая нагрузка рассчитывается по формуле:
где D p — диаметр штифта, а S su.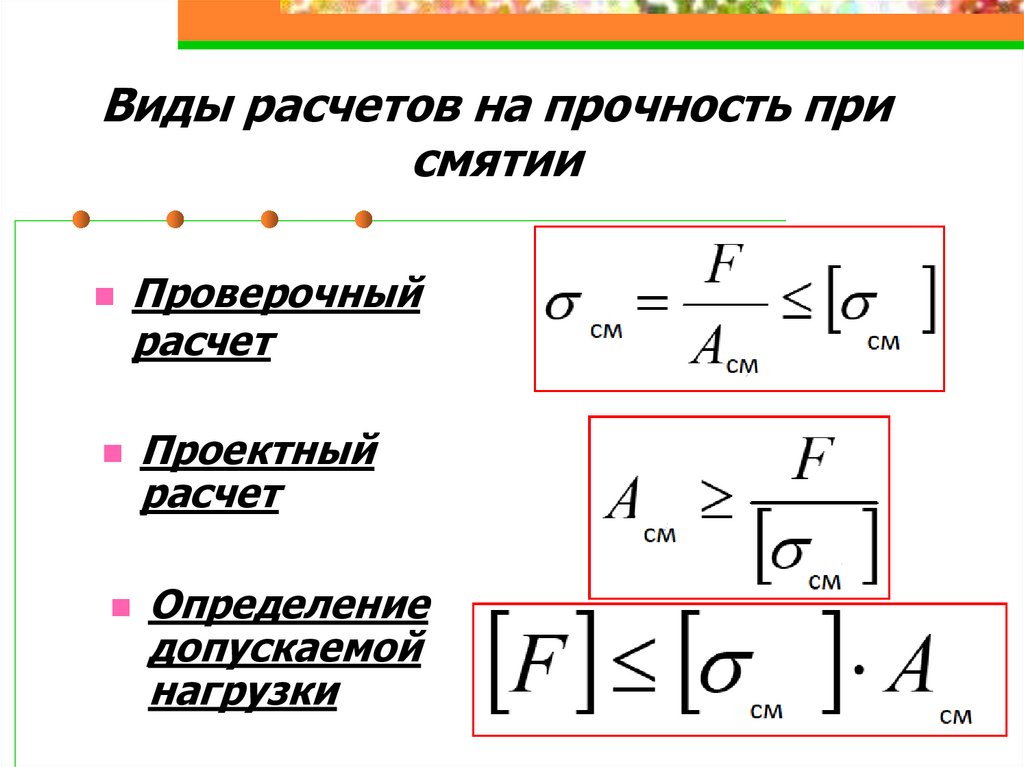 P — предел прочности на сдвиг материала штифта. Обратите внимание, что при расчете прочности штифта на сдвиг используется удвоенная площадь, поскольку существует две плоскости сдвига.
P — предел прочности на сдвиг материала штифта. Обратите внимание, что при расчете прочности штифта на сдвиг используется удвоенная площадь, поскольку существует две плоскости сдвига.
Прочность на изгиб штифта
Предельная изгибающая нагрузка — это приложенная нагрузка, которая может привести к разрушению штифта при изгибе, и рассчитывается по формуле:
где L плечо — плечо момента, а M u.P — предельный разрушающий момент для штифта. Если нагрузка распределяется равномерно по всей ширине проушин, то плечо момента рассчитывается по формуле:
где t 1 — толщина одиночной проушины с внутренней резьбой, t 2 — толщина проушины с охватываемой частью, а g — зазор между выступающей и охватывающей проушиной, когда проушина с наружной резьбой находится по центру между проушинами с внутренней резьбой.
Предельный разрушающий момент для штифта рассчитывается по формуле:
где S tu. P – предел прочности при растяжении материала штифта и k b.P – коэффициент пластического изгиба. Согласно Руководству ВВС, «значение k b.P варьируется от 1,0 для абсолютно эластичного штифта до 1,7 для идеально пластичного штифта со значением 1,56 для штифтов, изготовленных из достаточно пластичных материалов (удлинение более 5%). .»
P – предел прочности при растяжении материала штифта и k b.P – коэффициент пластического изгиба. Согласно Руководству ВВС, «значение k b.P варьируется от 1,0 для абсолютно эластичного штифта до 1,7 для идеально пластичного штифта со значением 1,56 для штифтов, изготовленных из достаточно пластичных материалов (удлинение более 5%). .»
Штифт Сильный или слабый на изгиб?
После расчета прочности штифта определите, является ли штифт сильным или слабым при изгибе. Если предельная нагрузка на изгиб штифта (P уб.Р ) больше либо предельной нагрузки на сдвиг штифта (Р ус.Р ), либо номинальной предельной нагрузки на соединение (Р у.Дж.ном ), то штифт относительно прочен и не критичен на изгиб. В противном случае штифт слаб и критичен на изгиб.
| P ub.P ≥ P u.J.nom или P ub.P ≥ P us.P ? | Да → прочный штифт |
| Нет → Слабый штифт |
Крепкий штифт
Если штифт прочный, прочность соединения будет ограничена либо прочностью штифта на сдвиг, либо номинальной прочностью соединения.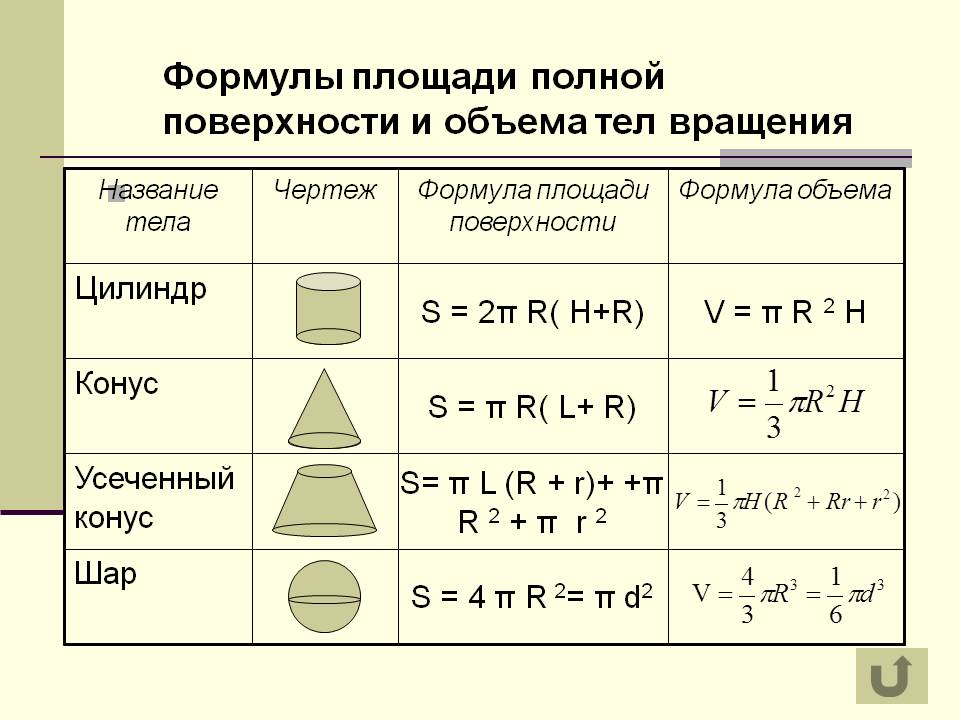 В случае прочного штифта предельная нагрузка на изгиб штифта рассчитывается при условии, что нагрузка распределяется равномерно по всей ширине выступов:
В случае прочного штифта предельная нагрузка на изгиб штифта рассчитывается при условии, что нагрузка распределяется равномерно по всей ширине выступов:
Уравнение, приведенное выше, такое же, как уравнение, представленное ранее для предельной нагрузки на изгиб штифта, но с членами, объединенными в одно уравнение.
Для прочного штифта изгиб штифта не влияет на прочность соединения, и предельная нагрузка на соединение равна номинальной предельной нагрузке на соединение:
P u.J. = P u.J.nom
Слабый штифт
Если штифт слаб на изгиб, то нагрузка не будет распределяться равномерно по ширине выступа. Вместо этого нагрузка будет концентрироваться в направлении плоскостей сдвига, а внутренние части выступов будут относительно разгружены. Из-за этого проушины выйдут из строя при более низкой нагрузке, чем предполагалось.
Чтобы учесть низкую прочность штифта на изгиб, рассчитывается предельная нагрузка «сбалансированной конструкции». Цель состоит в том, чтобы определить фактическую ширину опоры, на которой проушины воспринимают нагрузку. Вместо того, чтобы воспринимать нагрузку по всей толщине проушин, t 1 и t 2 , вместо этого нагрузка будет распределяться по некоторым меньшим ширинам, b 1 и b 2 , как показано на рисунке ниже. Предполагается, что нагрузка равномерно распределена по этим ширинам.
Цель состоит в том, чтобы определить фактическую ширину опоры, на которой проушины воспринимают нагрузку. Вместо того, чтобы воспринимать нагрузку по всей толщине проушин, t 1 и t 2 , вместо этого нагрузка будет распределяться по некоторым меньшим ширинам, b 1 и b 2 , как показано на рисунке ниже. Предполагается, что нагрузка равномерно распределена по этим ширинам.
Уменьшение ширины подшипника имеет два эффекта:
- Предельная нагрузка на проушины снижается (проушины выходят из строя при меньшей нагрузке).
- Плечо момента для штифта уменьшается, что увеличивает предельную нагрузку на изгиб штифта (штифт выходит из строя при более высокой нагрузке).
Новое, увеличенное значение предельной изгибающей нагрузки на штифт рассчитывается по формуле:
где в приведенном выше уравнении b 1 и 2·b 2 были заменены на t 1 и t 2 из предыдущего уравнения изгиба штифта.
Хитрость заключается в том, чтобы найти значения b 1 и b 2 , которые приводят к предельной нагрузке «сбалансированной конструкции». Чтобы определить предельную нагрузку сбалансированной конструкции, уменьшите ширину опоры каждой из проушин до тех пор, пока предельная нагрузка для проушин не станет равной друг другу, а также равной предельной нагрузке на изгиб штифта. Это требует итеративного процесса.
Как только будет найдена предельная нагрузка сбалансированной конструкции, предельная нагрузка на соединение и предельная нагрузка на изгиб штифта будут равны сбалансированной нагрузке:
P уб.J = P уб.P = P сбалансированный
Расчет допустимой нагрузки на соединение
Предельная нагрузка на сустав (P u.J ) должна была быть рассчитана в одном из двух предыдущих разделов, в зависимости от того, был ли штифт сильным или слабым при изгибе:
| Прочный штифт: | P u.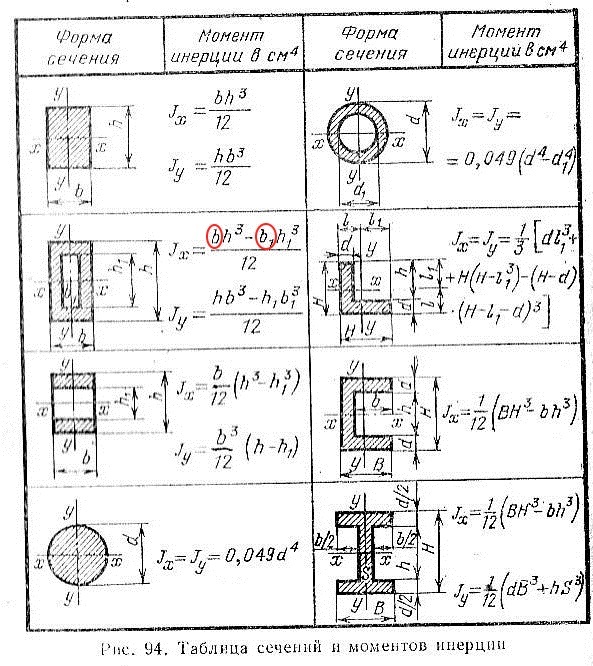 J. = P u.J.nom J. = P u.J.nom |
| Слабый штифт: | P u.J = P сбалансированный |
Общая предельная нагрузка, учитывающая как предельную нагрузку на соединение, так и предельную нагрузку на сдвиг штифта, рассчитывается по формуле:
P ult = min( P u.J , P us.P )
Коэффициент безопасности рассчитывается по формуле:
Нужен калькулятор люфта?
Попробуйте наш калькулятор тяги, основанный на методологии, описанной здесь.
- Допускает осевую, поперечную или наклонную нагрузку
- Выполнение расчетов прочности выступов, прочности штифтов и прочности соединения при двойном сдвиге
Метод ASME BTH
Метод ASME анализа проушин описан в ASME BTH-1, «Проектирование подъемных устройств под крюком». Этот метод рассматривает следующие виды отказов, где цифры соответствуют рисунку:
- Разрыв натяжения в секции сетки
- Разрушение при сдвиге по двум плоскостям
- Выход из строя подшипника
- Перелом в одной плоскости
Несмотря на то, что коэффициент запаса прочности при выпучивании (выпучивание вне плоскости) явно не рассчитывается, при расчете эффективной ширины учитывается толщина выступа в попытке защитить от разрушения выпуклости.
Размеры, представляющие интерес для анализа проушин, показаны на рисунке ниже:
Размеры на рисунке включают:
- D h = диаметр отверстия
- D p = диаметр штифта
- b e = ширина нетто (расстояние между краем отверстия и краем выступа в поперечном направлении)
- R = краевое расстояние (расстояние от центра отверстия до края выступа в направлении приложенной нагрузки)
- r = радиус кривизны края выступа (больше или равен R)
- a = расстояние от края отверстия до края выступа = R − 0,5 D h
- t = толщина (на рисунке не показано — толщина указана на странице)
- Z = потеря длины плоскости сдвига из-за кривизны на конце выступа
- ϕ = угол установки плоскости сдвига
Поправочные коэффициенты
Анализ в ASME BTH очень похож на упрощенный анализ, за исключением нескольких поправочных коэффициентов, которые рассчитываются на основе результатов испытаний. Эти поправочные коэффициенты обсуждаются ниже.
Эти поправочные коэффициенты обсуждаются ниже.
Понижающий коэффициент прочности
Прочность выступа уменьшается по мере ослабления посадки между штифтом и отверстием. Прочность выступа не сильно пострадает, если штифт и отверстие плотно прилегают друг к другу. ASME определяет коэффициент снижения прочности, который можно использовать для учета зазора между штифтом и отверстием, как:
где D p – диаметр штифта, а D h – диаметр отверстия.
Установочный угол плоскости сдвига
Угол расположения плоскости сдвига, ϕ, используется для определения положения двух плоскостей, вдоль которых происходит разрыв при сдвиге, как показано на рисунке:
Большее значение ϕ приводит к большей площади плоскости сдвига. Другие методологии обычно используют ϕ как постоянное значение (обычно 40 °), но ASME связывает его с отношением диаметра штифта к диаметру отверстия, так что штифт со свободной посадкой имеет меньшую площадь плоскости сдвига, чем штифт с плотной посадкой:
Эффективная ширина
Член b e обозначает ширину нетто и представляет собой расстояние между краем отверстия и краем выступа в поперечном направлении, как показано на рисунке:
При расчетах натяжения рассчитывается эффективная ширина , которая является наименьшей из следующих величин:
| • | b эфф.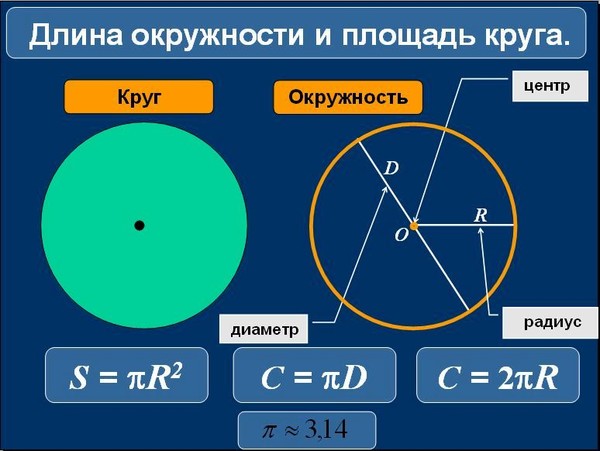 1 = b e 1 = b e |
Эффективная ширина не должна превышать фактическую чистую ширину. |
| • | б эфф.2 = 4 т | Этот предел предназначен для защиты от разрушения выпуклости (как только толщина выступа падает ниже 1/4 ширины нетто b e , эффективная ширина уменьшается). Этим ограничением можно пренебречь, если проушина усилена или стеснена против коробления. |
| • | Это уравнение является эмпирическим и адаптировано к результатам испытаний. |
Эффективная ширина рассчитывается как:
b эфф. = min( b эфф.1 , b эфф.2 , b эфф.3 )
Фактор конструкции и класс обслуживания
Расчетный коэффициент (т. е. требуемый запас прочности), N d , используется в расчетах прочности. Значение для N d можно найти в таблице ниже:
| Расчетный коэффициент | Состояние |
|---|---|
| N d = 2,00 | Подъемники категории A (предсказуемые нагрузки, точно определенные или нестрогие условия окружающей среды, не более 20 000 циклов нагрузки) |
| N d = 3,00 | Подъемники категории B (непредсказуемые нагрузки, неопределенные или тяжелые условия окружающей среды) |
Класс обслуживания используется для учета усталостной долговечности и определяется на основе приведенной ниже таблицы:
| Класс обслуживания | Циклы нагрузки |
|---|---|
| 0 | 0 — 20 000 |
| 1 | 20 001 — 100 000 |
| 2 | 100 001 — 500 000 |
| 3 | 500 001 — 2 000 000 |
| 4 | Более 2 000 000 |
Расчет прочности проушин
Эти расчеты прочности применимы только для осевых нагрузок, как показано стрелкой прилагаемой силы на рисунке ниже:
Чтобы определить, имеет ли проушина достаточную прочность, рассчитайте запас прочности для каждого из режимов отказа, описанных ниже. Пока приложенная сила находится в пределах допустимой нагрузки и пока каждый фактор безопасности является приемлемым, можно считать, что проушина пройдена.
Пока приложенная сила находится в пределах допустимой нагрузки и пока каждый фактор безопасности является приемлемым, можно считать, что проушина пройдена.
Прочность на растяжение
Предельная растягивающая нагрузка — это нагрузка, которая может привести к разрушению при растяжении по всей сетке, и определяется по формуле:
P в.у. = C r S в.у. A t
где C r — коэффициент снижения прочности, а S tu — предел прочности при растяжении проушины. A t представляет собой площадь сечения нетто и рассчитывается по формуле:
А т = 2 т б эфф
где b eff — эффективная ширина, t — толщина выступа.
Допустимая растягивающая нагрузка основана на расчетном коэффициенте N d , и выдается:
Обратите внимание, что допустимая растягивающая нагрузка основана на расчетном коэффициенте, умноженном на 1,20. ASME требует, чтобы расчетный коэффициент для некоторых расчетов прочности был выше номинального значения. Коэффициент безопасности определяется:
ASME требует, чтобы расчетный коэффициент для некоторых расчетов прочности был выше номинального значения. Коэффициент безопасности определяется:
Для соответствия ASME BTH коэффициент запаса прочности должен быть не менее 1,20·N d , но требуемый коэффициент запаса прочности может быть больше в зависимости от требований заказчика или инженерной оценки.
Прочность на излом в одной плоскости
Предельная нагрузка на разрушение в одной плоскости — это нагрузка, которая может привести к разрушению вдоль плоскости, коллинеарной приложенной нагрузке, и определяется как:
Р б.у = С р С ту А б
где C r — коэффициент снижения прочности, а S tu — предел прочности при растяжении проушины. A b — это эффективная площадь, которая рассчитывается как:
где R — расстояние до края, D h — диаметр отверстия, b e — ширина нетто, t — толщина выступа.
Допустимая нагрузка на разрушение в одной плоскости основана на расчетном коэффициенте N d и определяется по формуле:
Коэффициент безопасности определяется:
Прочность на излом в двух плоскостях
Предельная сдвигающая нагрузка в двух плоскостях — это нагрузка, которая может привести к разрыву при сдвиге вдоль двух плоскостей, и определяется по формуле:
Р в.у = 0,70 S вт А в
где C r — коэффициент снижения прочности, а S tu — предел прочности при растяжении проушины. v — это общая площадь двух плоскостей сдвига, которая определяется по формуле:
где ϕ — угол расположения плоскости сдвига, а Z — потеря длины плоскости сдвига из-за кривизны на конце выступа. Эта потеря рассчитывается как:
Обратите внимание, что если конец выступа плоский, то r равно бесконечности, а Z равно нулю.
Допустимая сдвигающая нагрузка в двойной плоскости основана на расчетном коэффициенте N d и определяется по формуле:
Коэффициент безопасности определяется:
Несущая способность
Предельная нагрузка на подшипник — это нагрузка, которая может привести к выходу из строя подшипника либо выступа, либо пальца. Эта предельная нагрузка зависит от количества циклов нагрузки, которым будет подвергаться соединение, и определяется как:
Эта предельная нагрузка зависит от количества циклов нагрузки, которым будет подвергаться соединение, и определяется как:
где S ty.min — минимальный предел текучести между ушком и пальцем (т.е. S ty.min = min(S ty.min , S ty.min )). Значение A p представляет собой площадь опоры пальца и рассчитывается по формуле:
А р = Д р т
Допустимая нагрузка на подшипник основана на расчетном коэффициенте N d и определяется по формуле:
Коэффициент безопасности определяется:
PDH Classroom предлагает курс повышения квалификации на основе этой справочной страницы по анализу наконечников. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.
Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!
Просмотреть курс сейчас:
Просмотреть курс
Приложение
Несоответствие с руководством ВВС — наклонная нагрузка
В Руководстве ВВС указывается, что коэффициент запаса прочности для проушины с наклонной нагрузкой необходимо вычислять путем проведения линии от начала координат, которая пересекает кривую допустимой нагрузки, где наклон линии определяется как:
где P u. L — предельная нагрузка для проушины с осевой нагрузкой, а P tru.L — предельная нагрузка для проушины с поперечной нагрузкой.
L — предельная нагрузка для проушины с осевой нагрузкой, а P tru.L — предельная нагрузка для проушины с поперечной нагрузкой.
Проблема с использованием приведенного выше уравнения для наклона заключается в том, что линия пересечения остается одной и той же независимо от угла приложенной силы. Эта проблема проиллюстрирована на рисунке ниже:
Если приложенная сила находится под углом 5°, так что она почти полностью аксиальна, то точка приложенной нагрузки будет лежать вдоль синей линии, как показано на рисунке, а точка пересечения должна отражать коэффициент безопасности, равный очень близко к таковому у проушин с аксиальной нагрузкой. Аналогичным образом, если приложенная сила находится под углом 85°, так что она почти полностью поперечна, то точка приложенной нагрузки будет располагаться вдоль красной линии, как показано на рисунке, а точка пересечения должна отражать коэффициент безопасности. это очень близко к чистому поперечно нагруженному выступу.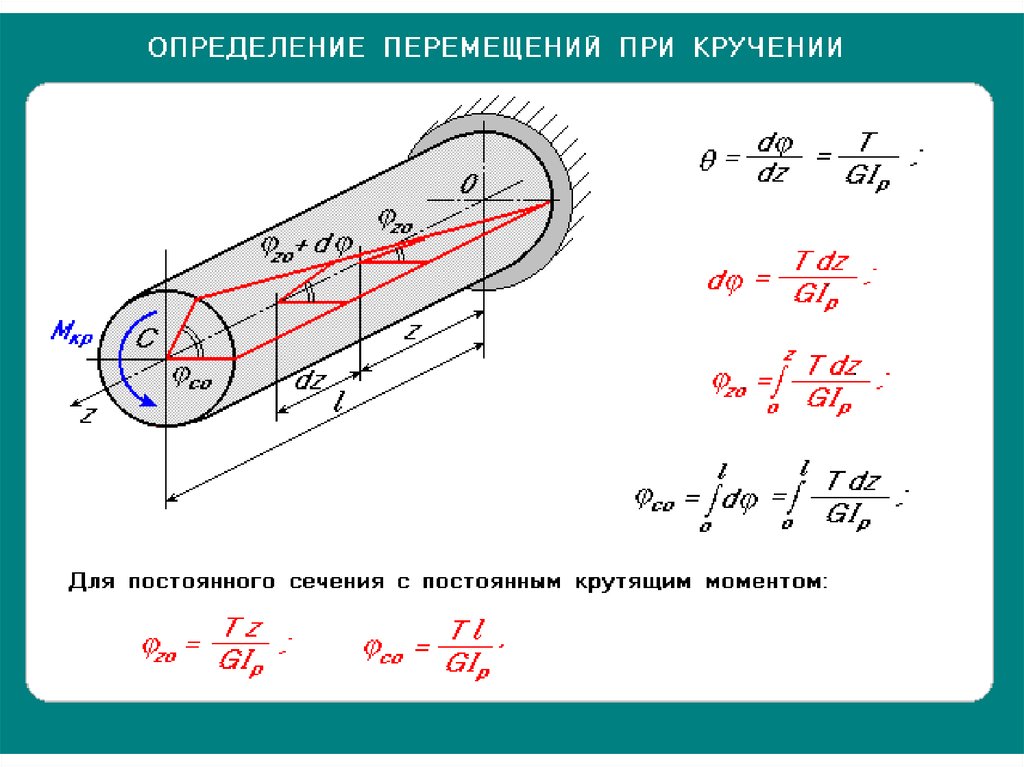 На основании этого рассуждения наклон линии должен отражать приложенное условие нагрузки:
На основании этого рассуждения наклон линии должен отражать приложенное условие нагрузки:
Примечания
Примечание 1. Относительный размер выступа и вилки
Следует отметить, что рисунок, показывающий проушину со штифтом, не точно отображает относительный размер. Штифт с плоской головкой должен относительно плотно входить в проушину. В соответствии с ASME диаметр штифта должен составлять не менее 90 % диаметра отверстия для проушины, чтобы избежать снижения прочности соединения.
Примечание 2. График коэффициента осевой нагрузки
Имена переменных, используемые на графике коэффициента осевой нагрузки из Руководства ВВС, несовместимы с остальными именами переменных в этом руководстве. Этот график был создан в Melcon & Hoblit, и имена переменных на графике не были обновлены для соответствия. В Руководстве ВВС используется переменная e для расстояния до края (от центра отверстия до края выступа) и a для расстояния между краем отверстия и краем выступа.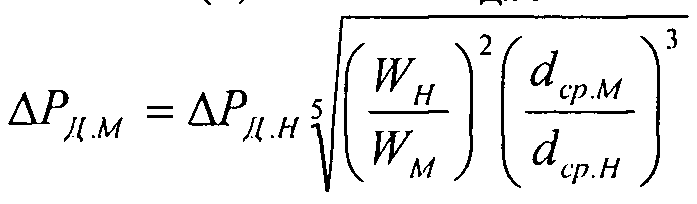 Однако на графике для расстояния до края (от центра отверстия до края выступа) используется a.
Однако на графике для расстояния до края (от центра отверстия до края выступа) используется a.
Примечание 3. Обратное среднее для размеров поперечных выступов
Эффективное краевое расстояние для проушин с поперечной нагрузкой рассчитывается с использованием обратного среднего значения. Эффект обратного среднего заключается в том, что в результате преобладают меньшие члены, так что непропорционально большое значение не приведет к значительному увеличению среднего, но непропорционально маленькое значение значительно снизит среднее (т.е. слабое звено — это тот же эффект наблюдается при последовательном размещении пружин). Использование этого уравнения для расчета эффективного краевого расстояния для проушины с поперечной нагрузкой было предложено Melcon и Hoblit. Они заявили, что причина коэффициента 3 на h 9Термин 0139 1 предназначался для уменьшения разброса их данных испытаний, но это имело смысл, поскольку в проушине с поперечной нагрузкой секция h 1 будет воспринимать большую часть нагрузки.
Примечание 4. Взаимосвязь между компонентами предельной нагрузки для наклонной нагрузки
Для расчета предельных составляющих нагрузки для наклонно нагруженного грунтозацепа необходимо определить взаимосвязь между предельными составляющими. Известно, что коэффициенты фактической нагрузки пропорциональны коэффициентам предельной нагрузки, поскольку эти коэффициенты лежат на одной линии нагрузки:
Выразите соотношения через составляющие нагрузки и упростите:
Компоненты нагрузки связаны углом приложения нагрузки:
Примечание 5: Коэффициент запаса прочности для наклонной нагрузки
Следует отметить, что коэффициент безопасности для проушины с наклонной нагрузкой может быть включен в саму кривую допустимой нагрузки следующим образом:
Тогда коэффициент запаса можно рассчитать непосредственно по формуле:
Подпишитесь, чтобы время от времени получать обновления о последних улучшениях:
Каталожные номера
- ASME BTH-1, «Проектирование подъемных устройств под крюком», Американское общество инженеров-механиков, 2014 г.

- Брюн, Э.Ф., «Анализ и проектирование конструкций летательных аппаратов», июнь 1973 г.
- Мелкон, М.А. и Ф.М. Hoblit, «Развитие анализа проушин и срезных штифтов», Product Engineering, 19 июня.53.
- Ниу, Майкл С., «Анализ напряжений и размеры планера», октябрь 2011 г.
- «Руководство по анализу напряжений», Лаборатория динамики полета ВВС, октябрь 1986 г.
Выбор и размеры тарелки дистилляционной колонны – 1
Введение:
После завершения этапа проектирования процесса начинается проектирование оборудования. На этом этапе проектирования требования процесса преобразуются в фактическое оборудование.
Одним из наиболее известных аппаратных средств, используемых для массообмена, является лоток. Тарельчатые колонны широко используются в различных видах массообменных операций. Все результаты моделирования, которые предсказывают определенное количество теоретических стадий, могут быть преобразованы в фактические лотки в зависимости от эффективности лотков для конкретной услуги.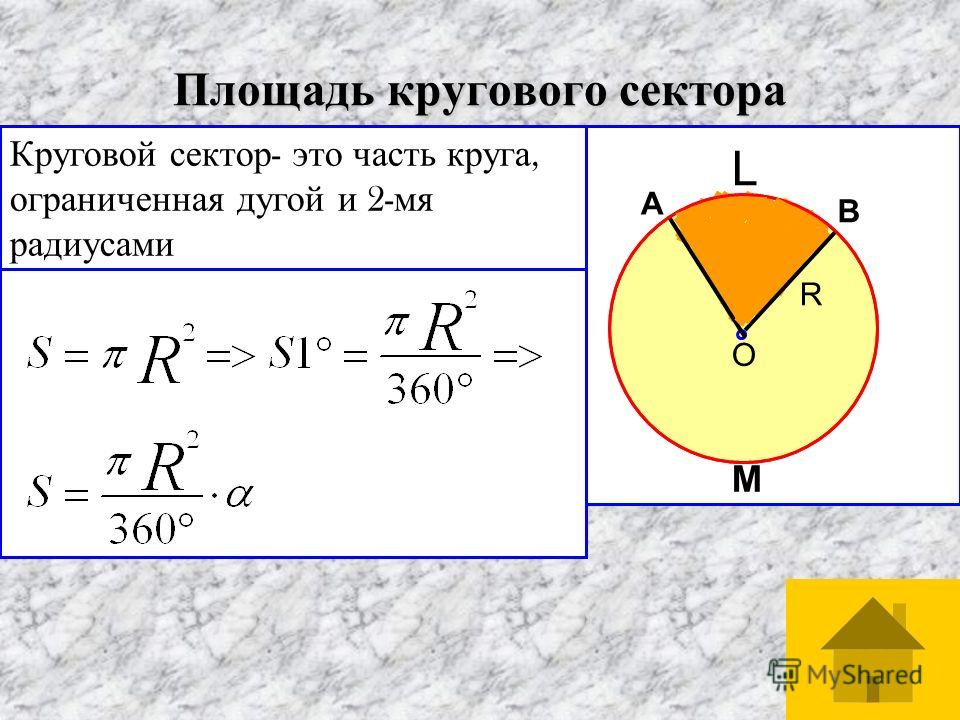
В любой обычной тарелке пар поднимается через бассейн жидкости на платформе тарелки, а затем отделяется от жидкости в пространстве над платформой. Жидкость поступает в тарелку из стояка сверху и выходит через слив снизу.
Обычный лоток имеет три функциональные зоны:
- Активная зона для смешивания пара и жидкости: это зона, в которой происходит массоперенос.
- Паровое пространство над активной зоной: это зона, в которой жидкость отделяется от пара.
- Перелив между тарелками. Эта зона выполняет две функции: во-первых, перемещение жидкости с одной контактной тарелки на другую, а во-вторых, отделение пара от жидкости.
Каждая из этих зон занимает вертикальное и горизонтальное пространство в башне.
Руководство по выбору колонны лотков:
Рассмотренные ниже факторы влияют на выбор между лотками и насадками. Поскольку это рекомендации по выбору тарелок или упаковок для конкретной услуги, при выборе рекомендуется проанализировать каждый проект отдельно.
|
Старший № |
Колонка для поддонов для системы | Система в пользу набивной колонки | ||||||||||
|
1 |
Твердое обращение | Вакуумная система | ||||||||||
|
2 |
Высокая дебит жидкости | Применение с низким перепадом давления | ||||||||||
| Подача | композиция и |
температура |
Модернизация — | давление | падение |
сокращение |
||||||
|
3 |
может быть | переведено в емкость | усиление, |
и |
||||||||
| переменная | ||||||||||||
прирост энергии или улучшение разделения. |
||||||||||||
|
4 |
Колонны большого диаметра | Колонны малого диаметра < 900 мм | ||||||||||
|
5 |
Легко прогнозировать производительность | Коррозионная система | ||||||||||
|
6 |
Меньше | вес | экономия | в | стоимость |
из |
Система пенообразования | |||||
| фундаменты и опоры | ||||||||||||
|
7 |
Интеркотлы, интерконденсаторы, охлаждение | Низкий | жидкость | ограбление | для |
уменьшение |
||||||
| цанги и боковая тяга | полимеризация и деградация.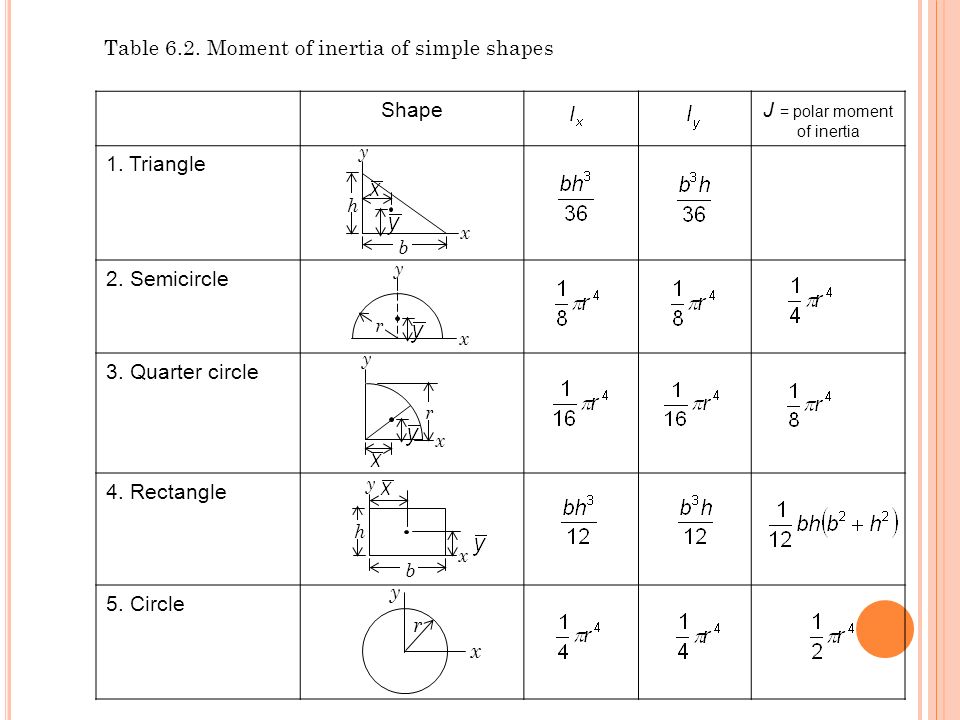 |
|||||||||||
|
8 |
Высокие требования к отказоустойчивости | Периодическая дистилляция | ||||||||||
|
9 |
Химические реакции |
Промышленность, основываясь на своем опыте, стандартизировала тип для использования в определенных услугах.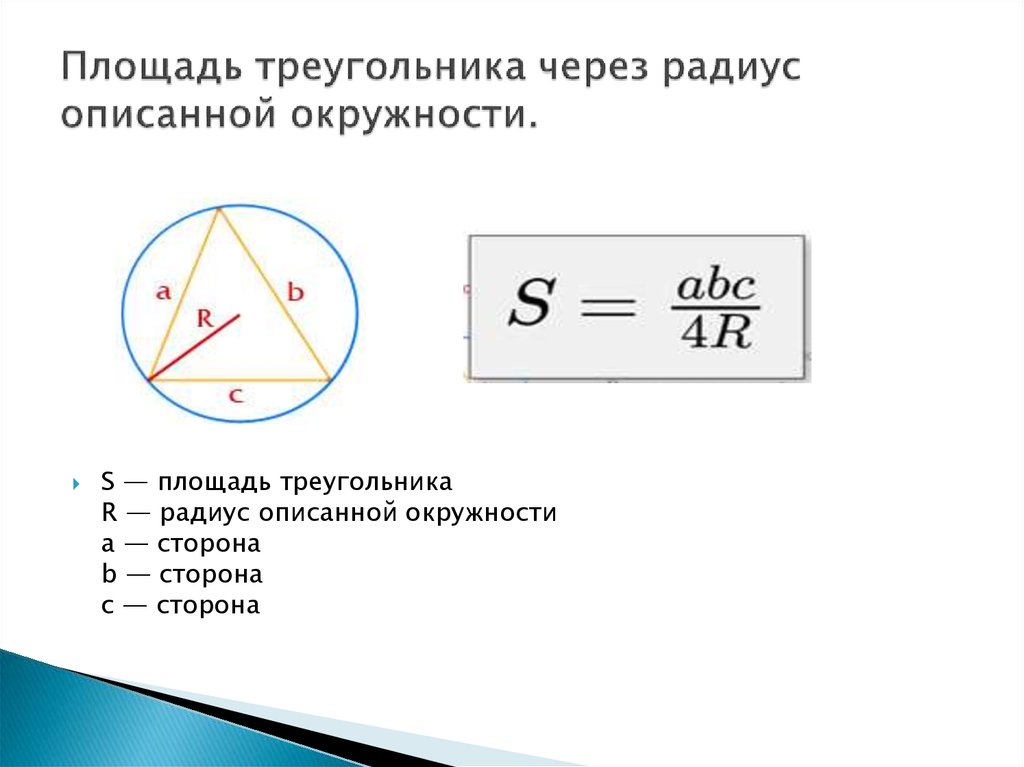 Если эта ссылка недоступна, следует использовать руководство согласно Приложению 1
Если эта ссылка недоступна, следует использовать руководство согласно Приложению 1
Типы тарелок
Выбор конкретной тарелки и ее конструкция могут существенно повлиять на производительность данной дистилляционной, абсорбционной или отпарной системы. Каждая тарелка должна быть сконструирована таким образом, чтобы обеспечить как можно более эффективный контакт между паром и жидкостью в разумных экономических пределах.
Клапанная тарелка:
Клапанная тарелка представляет собой платформу из перфорированного листового металла, на которой установлены круглые подъемные клапаны. Пар проходит через клапаны, установленные параллельно выходному водосливу. Клапанные тарелки сочетают в себе высокую производительность и превосходную эффективность с широким рабочим диапазоном.
Преимущества:
Превосходный контакт между жидкостью и паром.
Более высокая емкость.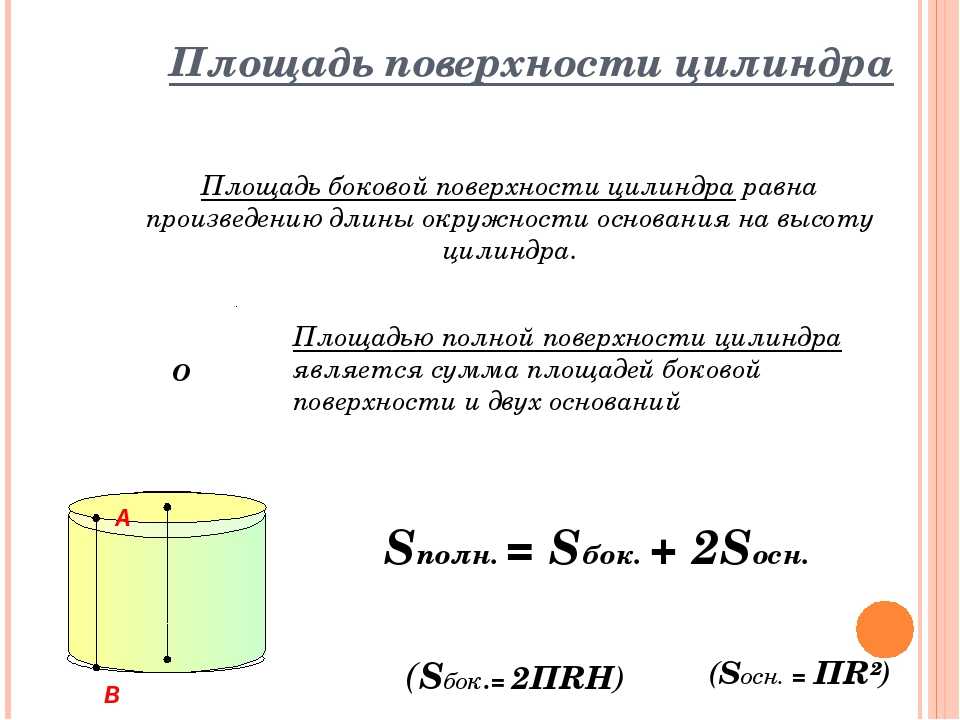
Более высокая гибкость, чем у ситчатых тарелок.
Может выдерживать более высокие нагрузки.
Низкий перепад давления по сравнению с колпачком.
Ситчатая тарелка:
Ситчатая тарелка представляет собой плоскую перфорированную пластину, в которой пар поднимается через небольшие отверстия в дне тарелки и образует пузырьки через жидкость довольно равномерно. Они имеют сравнимую емкость с клапанными тарелками.
Преимущества:
Простой строительство Низкое увлечение,
Низкая стоимость низкой стоимости технического обслуживания
Низкая тендента
Лоток для колпачков:
Пар поднимается по стоякам или всасывается в колпачок, выходит через прорези в виде пузырьков в окружающую жидкость на тарелке. Он в основном используется в специальных приложениях.
Преимущества:
Умеренная производительность
Самая гибкая (высокая и низкая скорость испарения и жидкости)
Может обеспечить отличный динамический диапазон.
Недостатки:
Высокий увлечение, склонность высокого загрязнения
Высокая стоимость,
Высокий перепад давления
Двухпоточные тарелки:
Двухпоточные тарелки представляют собой ситчатые тарелки без сливных стаканов. Этот лоток работает с жидкостью, непрерывно просачивающейся через отверстия. Благодаря отсутствию сливных стаканов двухпоточная тарелка имеет большую площадь тарелки и, следовательно, большую производительность, чем любой из обычных типов тарелки. Они идеально подходят для модернизации, когда можно пожертвовать некоторой эффективностью ради большей емкости. Они наименее дороги в изготовлении и просты в установке и обслуживании.
Пефлярный лоток с двойным потоком
Перегородные лотки:
Для столбца лотка с перегородкой. Газ течет вверх через перегородки и при этом контактирует с душами жидкости от одной печи к следующей. Колонны с разделительной тарелкой имеют почти такую же пропускную способность, что и тарелки с поперечным потоком. Используемые типы перегородок: дисковые и кольцевые, а также сегментные перегородки для колонн различного диаметра.
Колонны с разделительной тарелкой имеют почти такую же пропускную способность, что и тарелки с поперечным потоком. Используемые типы перегородок: дисковые и кольцевые, а также сегментные перегородки для колонн различного диаметра.
Лотки с двойным потоком и перегородкой используются для удаления отложений, работы с твердыми частицами/шламами, коррозионно-активных сред.
Собственные типы лотков:
Лотки MD – Linde / UOP,
Лотки Ripple – Stone & Webster Engg. Corp.
Прямоугольный клапан (BDH),
ValveGrid (MVG/SVG),
SHELL HIFI, лотки ConSep — лоток SulzerBallast,
Flexitray, тарелки Bi-FRAC, SUPERFRAC и ULTRAFRAC — Koch-Glitsch Engg.Co. , Туннельные лотки — Монц,
Поддоны Nye- Nye Engg Co,
Сравнение стандартных подносов .
| Старший | Факторы | Ситчатый лоток | Клапанная тарелка | Лоток для колпачков | Двухпоточный лоток | |
| № | ||||||
| 1 | Емкость | Высокий | Высокий |
Умеренно высокий |
Очень высокий |
|
| 2 | Эффективность | Высокий | Высокий |
Умеренно высокий |
Минимум |
|
| 3 | Диапазон регулировки | ~50% | ~25-30% |
10% |
Минимум |
|
| 4 | Унос | Умеренный | Умеренный |
Высокий |
От низкого до умеренного | |
| 5 | Падение давления | Умеренный | Умеренный |
Высокий |
От низкого до среднего | |
| 6 | Стоимость | Низкий | ~1,2 раза |
~ 2-3-кратное сито |
Минимум |
|
| ситчатые тарелки |
лотков |
|||||
| 7 | Техническое обслуживание | Низкий | Низкий до |
Относительно высокий |
Низкий |
|
| Умеренная | ||||||
| 8 | Загрязнение | Низкий | Низкий до | Высокий: имеет тенденцию собирать | Чрезвычайно низкий уровень | |
| Тенденция | Умеренный | Твердые вещества | ||||
| 9 | Эффекты | Низкий | Низкий до | Высокий | Очень низкий | |
| Коррозия | умеренный | |||||
| Собственность, | Немного информации | |||||
| Дизайн | Доступно. Нестабильность Нестабильность |
|||||
| 10 | Хорошо известно | но легко | Хорошо известно | |||
| информация | может встречаться в большом | |||||
| в наличии | ||||||
| диам. (>8 футов) | ||||||
| Часто используется | Где высокий | Чрезвычайно низкая жидкость | Модернизация мощностей, | |||
| Главный | поток и где | |||||
| 11 | при отказе | динамический диапазон равен | Сильно загрязняется и | |||
| Заявка | утечка должна быть | |||||
| не критично | требуется | коррозионные услуги | ||||
| свернут | ||||||
Параметры лотка
a) Количество проходов (N p 5):2206
Количество путей потока жидкости на тарелке: 1, 2, 3 или 4 в соответствии с требованиями по емкости колонны.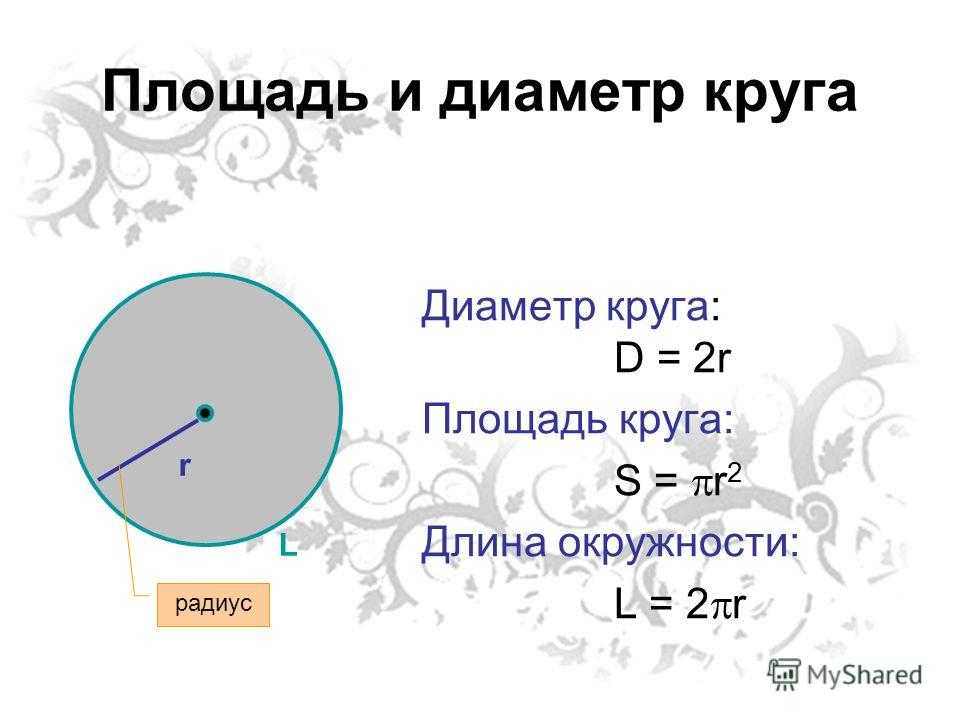 С точки зрения пропускной способности, расход жидкости выше 6 галлонов в минуту на дюйм водослива (нагрузка на водослив) является расходом, при котором следует учитывать большее количество путей потока. Максимально допустимая нагрузка на водослив составляет 13 галлонов в минуту на дюйм длины водослива. Если нагрузка на водослив превышает это значение, необходимо изменить конструкцию лотка с увеличением количества проходов.
С точки зрения пропускной способности, расход жидкости выше 6 галлонов в минуту на дюйм водослива (нагрузка на водослив) является расходом, при котором следует учитывать большее количество путей потока. Максимально допустимая нагрузка на водослив составляет 13 галлонов в минуту на дюйм длины водослива. Если нагрузка на водослив превышает это значение, необходимо изменить конструкцию лотка с увеличением количества проходов.
б) Расстояние между лотками (S):
Расстояние между лотками — это расстояние между двумя лотками. Обычно расстояние между лотками составляет от 8 до 36 дюймов (от 200 до 900 мм). Основным фактором при выборе расстояния между тарелками является экономический компромисс между высотой колонки и ее диаметром. Большинство колонн имеют расстояние между лотками 600 мм. Криогенные колонны имеют шаг тарелок 200-300 мм.
c) Водосливы на выходе (hw):
Водослив на выходе поддерживает желаемый уровень жидкости на тарелке. По мере того как жидкость покидает контактную зону тарелки, она течет по водосливу тарелки и попадает в сливной стакан.
По мере того как жидкость покидает контактную зону тарелки, она течет по водосливу тарелки и попадает в сливной стакан.
D) Зазор вниз (H CL ):
Это версическое расстояние между носом лотка и нижним краем вниз. Обычная практика заключается в использовании зазора сливного стакана на 1/2 дюйма меньше высоты переливного водослива для обеспечения статического жидкостного уплотнения
e) Впускные водосливы и утопленные уплотнительные поддоны:
Впускные водосливы и утопленные уплотняющие поддоны в основном используются для обеспечения герметичности сливного стакана в случаях, когда существует потенциальная проблема с принудительной герметизацией, а зазор под сливным стаканом ограничен
f) с верхней тарелки на нижнюю тарелку осуществляется через сливные трубы. Сливные трубы представляют собой каналы с круглым, сегментным или прямоугольным поперечным сечением, по которым жидкость переносится с верхней тарелки на нижнюю тарелку дистилляционной колонны.
Сливные трубы представляют собой каналы с круглым, сегментным или прямоугольным поперечным сечением, по которым жидкость переносится с верхней тарелки на нижнюю тарелку дистилляционной колонны.
g) Ширина сливного стакана (высота хорды, W DC ):
90 139 максимальное расстояние между стеной и водосливом.
h) Длина пути потока (FPL):
Длина пути потока – это расстояние между входным и выходным сливными стаканами. Минимальное ограничение длины пути потока составляет 400 мм, чтобы обеспечить хороший контакт между паром и жидкостью. Это также необходимо по механической причине обеспечения люка для поддона.
i) Толщина настила лотка (т):
Лотки, обычно используемые в коммерческих целях, должны иметь минимальную толщину материала, чтобы обеспечить структурную прочность (персонал ходит по ним) и допуск на коррозию. Толщина от 10 до 12 (от 2,5 до 3,5 мм) является обычной для углеродистой стали, а от 12 до 14 (от 1,9 до 2,5 мм) используется для лотков из нержавеющей стали (как правило, нет C.A. для SS)
Толщина от 10 до 12 (от 2,5 до 3,5 мм) является обычной для углеродистой стали, а от 12 до 14 (от 1,9 до 2,5 мм) используется для лотков из нержавеющей стали (как правило, нет C.A. для SS)
j) Шаг отверстий (P):
Расстояние между центрами отверстий называется шагом. Обычной практикой является использование отношения шага отверстия к диаметру от 2,2 до 3,8.
k) Факторы снижения номинальных характеристик системы:
Факторы снижения номинальных характеристик часто тесно связаны со склонностью системы к пенообразованию. Чем выше склонность к пенообразованию, тем ниже коэффициент снижения характеристик. Системные факторы используются в трех рейтинговых корреляциях (струйный паводок, резервный паводок в нижнем углу, штуцер в нижнем углу) для учета влияния системы на пределы гидравлической мощности.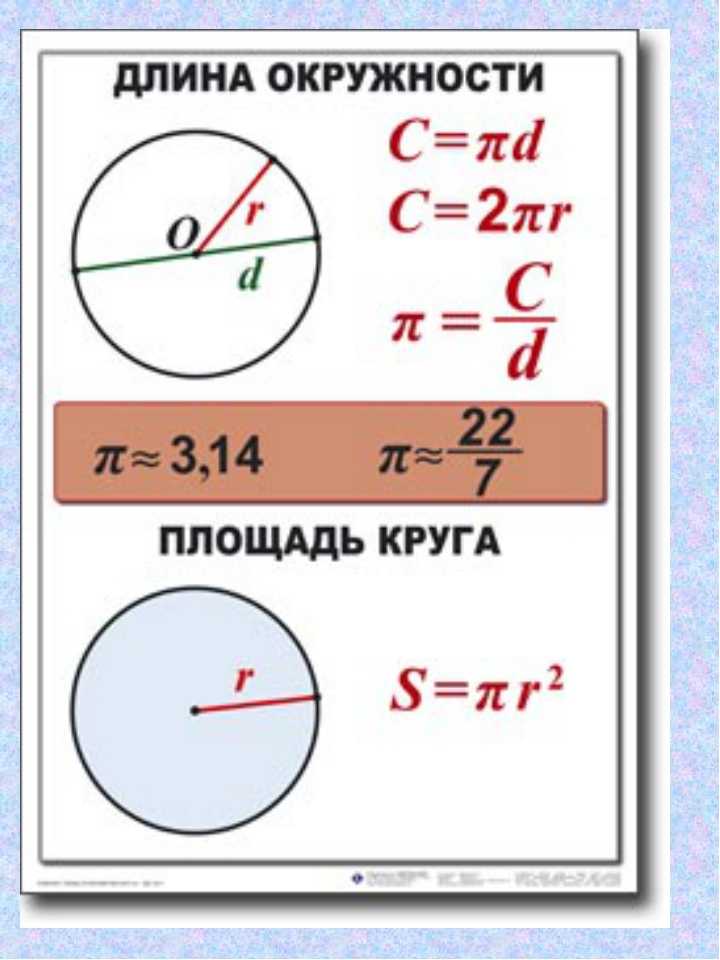 Он включает в себя как эффект пенообразования, так и высокую плотность пара.
Он включает в себя как эффект пенообразования, так и высокую плотность пара.
л) БУБЛИНА (АКТИВНАЯ) Зона (A B ):
. Его можно определить как площадь колонны за вычетом площадей стояка, уплотнения стояка и больших зон успокоения.
м) % Площадь отверстия:
Это отношение площади отверстия к площади пузырьков. Практика по умолчанию заключается в том, чтобы ориентироваться на площадь отверстия от 8 до 10 % площади пузырьков для работы под давлением. Приемлемый диапазон процентной площади отверстия составляет от 5 % до 15 %. Однако для некоторых критических сервисов мы можем довести % площади дыры до 17-17,5% при условии, что плач находится под контролем. Площади отверстий менее 5 % не используются.
n) Перегородки против прыжков:
Пластины перегородок против прыжков, подвешенные вертикально над центральными или смещенными от центра сливными стаканами, предотвращающие перетекание жидкости с одной деки на противоположную, гидравлический канал
2 Параметр 2 Лоток 92
Ниже приведены некоторые важные выходные параметры гидравлики лотка.
a) Затопление:
Струйное затопление:
В режиме распыления захлебывание вызывается избыточным потоком пара, что приводит к захвату избыточного количества жидкости паром вверх по колонне. В пенном и эмульсионном режимах работы избыточный унос пены с паром вверх по колонне вызывает захлебывание струи.
Резервный перелив в сливной стакан:
Происходит, когда давление, доступное для данной высоты жидкости и пены в сливном стакане, не может преодолеть общий перепад давления на тарелке. до тех пор, пока не достигнет верхнего лотка, вызывая повышенное скопление жидкости на нем. Он требует высокой нагрузки жидкости и пара.
Затопление штуцера сливного стакана:
Механизм возникновения этого типа затопления связан с чрезмерными потерями давления на трение в сливном стакане. Кроме того, пар, поступающий в сливной стакан, должен отделяться от жидкости и затем течь в противотоке к жидкости, поступающей в сливной стакан. Когда сочетание выходящего пара и поступающей жидкости становится чрезмерным, вход сливного стакана забивается, в результате чего жидкость скапливается на тарелке. Это требует относительно высоких дебитов жидкости, превышающих ограничение скорости сливного стакана.
Когда сочетание выходящего пара и поступающей жидкости становится чрезмерным, вход сливного стакана забивается, в результате чего жидкость скапливается на тарелке. Это требует относительно высоких дебитов жидкости, превышающих ограничение скорости сливного стакана.
b) Плач/слив
Давление пара недостаточно для удержания жидкости на лотке. Поэтому жидкость начинает просачиваться через перфорации.
c) Падение давления:
Падение давления является важным фактором при проектировании тарелки. Для вакуумных систем это становится более критичным, чем для систем высокого давления. Падение давления на тарелке рассматривается как сумма перепада давления на клапанах или ситах и падения давления на аэрируемой жидкости на платформе тарелки.
d) Диапазон регулирования:
Диапазон регулирования определяет диапазон паровой нагрузки, в пределах которого колонна может работать без существенного влияния на ее основную цель разделения (т. е. эффективность фракционирования) или при котором достигается приемлемая производительность тарелки. Эффективность тарелки остается на уровне проектного значения или превышает его во всем диапазоне регулирования.
е. эффективность фракционирования) или при котором достигается приемлемая производительность тарелки. Эффективность тарелки остается на уровне проектного значения или превышает его во всем диапазоне регулирования.
Размер лотка
Процедура определения размера представляет собой итеративный расчет. Устанавливается предварительный проект, который затем уточняется путем сверки с корреляциями производительности до тех пор, пока не будет достигнут адекватный проект. Расчеты размера выполняются в точке, где ожидается, что нагрузка на колонну будет самой высокой и самой низкой для каждой секции, т. е.
i) Верхний лоток
ii) Над каждой подачей, раздачей продукта или точкой добавления или удаления тепла.
iii) Под каждой подачей, отбором продукта или точкой подвода или отвода тепла.
iv) Нижний лоток.
v) В любой точке колонны, где расчетная нагрузка пара или жидкости достигает максимума
Калибровка выполняется во всех вышеуказанных точках нагрузки, а также проверяется детальная калибровка во всех вышеуказанных точках нагрузки.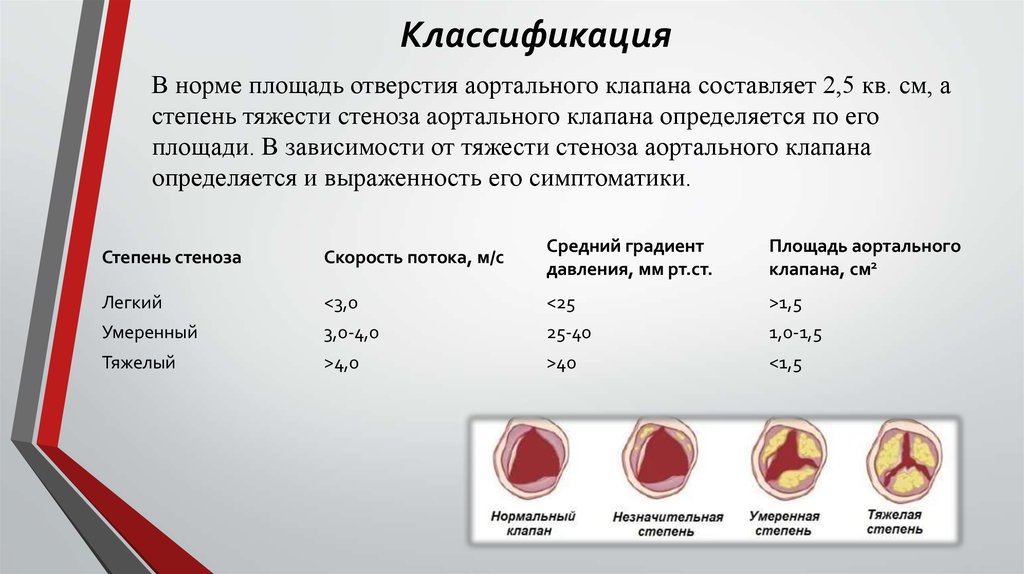 Все расчетные параметры, приведенные в приведенной ниже процедуре расчета, рассчитываются для всех указанных выше точек нагрузки при перегрузке и перегрузке таким образом, чтобы проверить осуществимость расчета при различных нагрузках.
Все расчетные параметры, приведенные в приведенной ниже процедуре расчета, рассчитываются для всех указанных выше точек нагрузки при перегрузке и перегрузке таким образом, чтобы проверить осуществимость расчета при различных нагрузках.
а) Предварительное определение площади башни:
Методы, используемые для определения диаметра башни:
- Метод коэффициента «С»
- Номографический метод
- Руководство по проектированию лотков FRI
Однако в этом техническом руководстве мы описываем метод с использованием метода С-фактора.
Метод C-фактора:
Следующие расчеты выполняются для всех точек нагрузки, упомянутых выше, и диаметры определяются отдельно. Если разница в расчетном диаметре на разных участках превышает 20 процентов, разные диаметры участков, вероятно, будут экономичными. Секция с другим диаметром должна быть не менее 20 футов в длину, в противном случае можно сохранить тот же диаметр.
и. Площадь лотка
Примите соответствующие значения для следующих параметров (исходя из требований системы) для предварительного расчета диаметра.
d H = Диаметр отверстий, дюймы (от ¼ до ½ дюйма) S = Расстояние между тарелками, дюймы (18 – 24″) жидкости.
Допущение: начальные значения для них могут быть d H =1/4″, S=24″, h ct =2″
Рассчитайте C-фактор (C SB ), используя следующую корреляцию Кистера и Хааса:
ii. Flood Velocity Calculation
Это скорость восходящего пара, при которой капли жидкости находятся во взвешенном состоянии. Рассчитайте скорость наводнения ( u N ) , используя следующую формулу:
iii. Расчет площади нетто
Площадь нетто представляет собой наименьшую площадь, доступную для потока пара в пространстве между тарелками.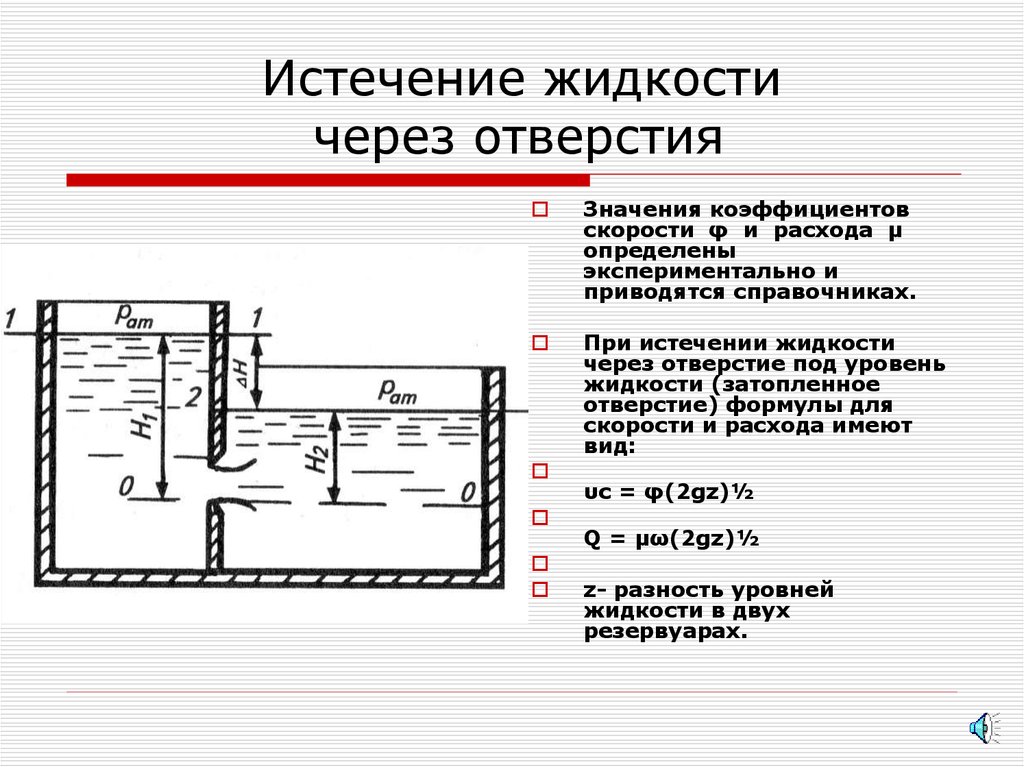 Вычислить площадь нетто (A N ) из скорости потока с использованием следующего уравнения: Предположим, что колонна должна быть рассчитана на 80% потока.
Вычислить площадь нетто (A N ) из скорости потока с использованием следующего уравнения: Предположим, что колонна должна быть рассчитана на 80% потока.
iv. Расчет области площади нижнего приема Расчет области вниз (A D ) из прозрачной скорости жидкости в добыче с использованием следующей формулы:
, где
Q L
,
Q L = Liquid,
Q L = Liquid,
. /с
В CL = Скорость чистой жидкости в сливном стакане
Значение V CL получено из таблицы ниже. Для этого расчета не требуется коэффициент снижения характеристик, так как значения V CL учитывают пенообразование
Пример
V CL в сливном стакане, фут/с
18-дюймовый
24 дюйма
30-в
Тенденция
Интервал
Интервал
Интервал
Низкий
Легкий углеводород низкого давления (<100 фунтов на кв. дюйм),
дюйм),
0,4-0,5
0,5-0,6
0,5-0,6
стабилизаторы, тренажеры воздух-вода
Средний
Масляные системы, перегонка сырой нефти, абсорберы,
0,3-0,4
0,4-0,5
0,4-0,5
мед. давление (100-300 фунтов на квадратный дюйм) углеводородное
Высокий
Амин, глицерин, гликоли, высокого давления
0,2-0,25
0,2-
0,2-0,3
(>300 psi) легкие углеводороды
0,25
v. Tower Diameter Calculation
Tower Diameter Calculation
TotalTowerArea (A T ) = A D + A N
b) Preliminary расположение лотков:
A Необходим предварительный макет, так как макет влияет на размер столбца.
Схема стояка:
Проверьте % площади стояка по отношению к площади башни:
Дробная площадь должна составлять около 10%, но при нормальных обстоятельствах следует избегать менее 8%. Обратите внимание, что A D ни при каких обстоятельствах не должен быть меньше 5% от A T
Чистая площадь (A N ):
Общая площадь поперечного сечения градирни A T за вычетом площади в верхней части сливного стакана (иногда называемой свободной площадью, термином свободная площадь).
Чистая площадь представляет собой наименьшую площадь, доступную для потока пара в межлотковое расстояние.
A N = A T – A D
Bubbling (Active) area (A B ):
Общая площадь поперечного сечения A T за вычетом площади на входе и выходе сливного стакана называется барботажной площадью.
A B = A T – A DT – A DB
Below figure shows the Typical Схема лотка.
Длина водослива и ширина сливного стакана: Лоток SinglePass:
Расчет длины водослива и ширины сливного стакана включает геометрическое соотношение между площадью сливного стакана, шириной сливного стакана и длиной сливного стакана.
На следующем рисунке показана геометрия сливного стакана:
Рассчитайте ширину сливного стакана и длину водослива, используя следующий метод
? = sin -1 (h/R)
w = 2*R COS ( ? ) или w = 2*(R 2 – h 2 ) 0,5
? /2 = ? /2 – ?
Площадь сектора = A SECT = ? Р 2 * ? / (2 * ? )
Площадь треугольника (ABC) = A TRI. = w*h/2
Где,
L w = Длина водослива = w* (1 частное засорение водослива)
w dc = Ширина сливного стакана = R-h A =1 A dc = Площадь сливного стакана
Частичное засорение водослива — это часть общей длины водослива, доступная для потока жидкости при использовании водослива типа пикет и забор.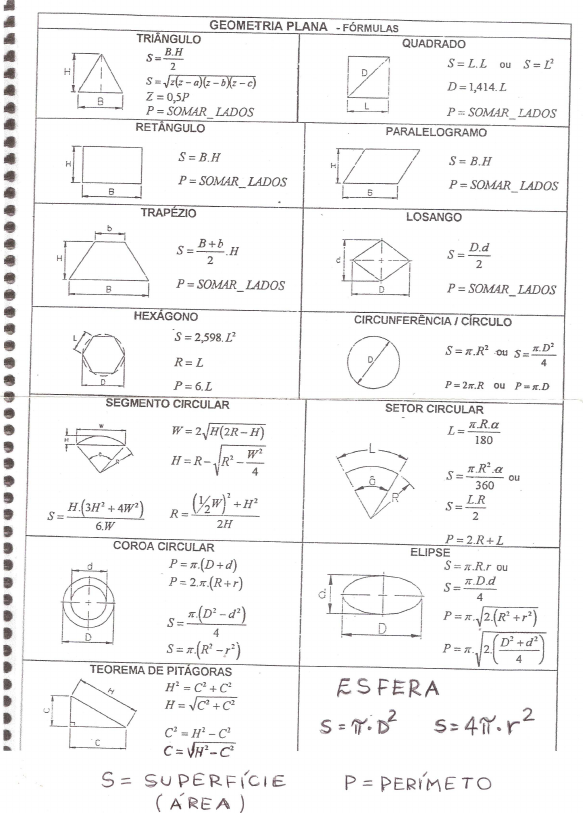 Заблокированные (штакетник) водосливы используются для работы с низкой нагрузкой жидкости.
Заблокированные (штакетник) водосливы используются для работы с низкой нагрузкой жидкости.
Зона нижнего стакана
A D = A SECT – A TRI
Двухпроходной лоток:
Два проходных лотка имеют чередующееся расположение одного стока в центре и двух боковых стоков.
Площадь бокового сливного стакана можно рассчитать как для однопроходного лотка. Следует отметить, что боковые сливы есть с обеих сторон.
Расчеты для центрального сливного стакана можно выполнить следующим образом аналогично боковому сливному стакану:
? = SIN -1 (H/R)
W = 2*R COS (? 1) или W = 2*(R 2 -H 2 ) 0,5
? = 2*( ? /2- ? )
Площадь сектора = ASECT = ? Р 2 * ? / (2 * ? )
Площадь центрального сливного стакана = Площадь круга -2*площадь сектора + 2*Площадь треугольника Площадь сливного стакана = ? *R 2 – 2* ASECT + h2*w1
В случае более чем двух проходных лотков мы должны определить еще один параметр, т. е. расположение сливного стакана не по центру от осевой линии. Это необходимо делать в каждом конкретном случае.
е. расположение сливного стакана не по центру от осевой линии. Это необходимо делать в каждом конкретном случае.
Длина пути потока жидкости (FPL):
ForSinglePassTray:
FPL= (диаметр лотка) минус (боковая ширина лотка DC) минус (ширина дна DC лотка вверху)
5
Где,
| w1 dc |
= |
Ширина сливного стакана (центральный сливной стакан, низ сливного стакана) |
| w2 постоянный ток |
= |
Ширина сливного стакана (боковой сливной стакан, верхняя часть сливного стакана) |
| w3 постоянный ток |
= |
Ширина сливного стакана (центральный сливной стакан, верхняя часть сливного стакана) |
| w4 постоянный ток |
= |
Ширина сливного стакана (боковой сливной стакан, нижняя часть сливного стакана) |
C) Рабочий проект
Проверка на затопление:
Проверка на затопление выполняется с использованием следующих соотношений:
- Корреляция Кистера и Хааса.
- Корреляция дросселя сливного стакана-Коха
- Корреляция ярмарки
- Смит и др. корреляция
1. Струйное заводнение: корреляция Кистера и Хааса
Эта корреляция обладает следующим преимуществом:
– Она дает близкое приближение к влиянию физических свойств, рабочей переменной и геометрии тарелки на точку затопления.
– Описывает унос режима распыления.
– Он был получен из гораздо более широкой базы данных коммерческих и пилотных столбцов данных.
— Он может прогнозировать затопление сита и тарелки клапана в пределах ± 15 и ± 20 процентов соответственно.
Данная корреляция имеет следующие ограничения:
| Sr.no. | Факторы | Применимость |
| 1 | Заливной механизм | Унос (струйный) только затопление |
| 2 | Тип лотка | Только ситчатые или клапанные тарелки |
| 3 | Давление | 1,5–500 фунт/кв. дюйм абс. дюйм абс. |
| 4 | Скорость газа | 1,5–13 фут/с |
| 5 | Жидкая загрузка | 0,5-12 гал/мин/дюйм водослива |
| 6 | Плотность газа | 0,03–10 фунт/фут3 |
| 7 | Плотность жидкости | 20-75 фунтов/фут3 |
| 8 | Поверхностное натяжение | 5-80 дин/см |
| 9 | Вязкость жидкости | 0,05-2,0 сП |
| 10 | Расстояние между лотками | 14-36 в |
| 11 | Диаметр отверстия | 1/8-1 дюйма |
| 12 | Дробная площадь отверстия | 0,06-0,20 |
| 13 | Высота плотины | 0-3 в |
Шаги для расчета % затопления с использованием корреляции Кистера и Хааса:
i. Расчет водосливной нагрузки (Q L ):
Расчет водосливной нагрузки (Q L ):
Жидкостная нагрузка описывает поток жидкости через тарелку.
ii. Прозрачная Высота жидкости при переходе от пены к брызгам ((h ct )
2. Jet Flood: Корреляция Fair
Корреляция Fair является стандартом в отрасли для прогнозирования паводков. Корреляция Fair имеет тенденцию быть консервативной, особенно при высоком давлении и дебите жидкости.
Это соотношение имеет следующие ограничения:
|
Старший № |
Факторы | Применимость | |
|
1 |
Заливной механизм | Унос (струйный) только затопление | |
|
2 |
Тип лотка | Лоток с ситом, клапаном и лотком с колпачком | |
|
3 |
Размер отверстия | Отверстие £ ½ дюйма (сетчатый лоток) | |
| Высота водослива | Расстояние между лотками < 15 % |
Шаги для расчета % наводнения с использованием корреляции Фэйра:
i. Рассчитать параметр расхода
Рассчитать параметр расхода
3. Корреляция дросселя нижнего стакана-Коха:
Это более консервативная корреляция для проверки конструкции нижнего стакана. Steps to calculate % Load Utilization using Kister and Haas correlation:
4. Hydraulic checks
Hydraulic check involves checking following parameters:
– Flow Regime
– Entrainment
– Downcomer residence time
– Падение давления
– Резервный стояк
ii. Определение режима потока
Пенный режим
Это наиболее часто встречающийся режим потока в действующих колоннах. Пена, образующаяся при этом режиме, описывается как пена, в которой размер и форма пузырьков неоднородны и имеют довольно большое распределение по размерам, а также перемещаются с различными скоростями. Поверхность жидкости либо волнистая, либо совершает колебания. Это режим непрерывного течения жидкости.
Это режим непрерывного течения жидкости.
Режим опрыскивания
Этот режим имеет место при относительно высоких скоростях пара (т.е. при больших скоростях потока пара) и низких жидкостных нагрузках, характерных для вакуумных систем. Скорость пара настолько велика, что жидкая фаза полностью разрушается и больше не является непрерывной фазой на поверхности тарелки; жидкость — это дисперсная фаза, присутствующая только в виде капель, поэтому сплошная фаза — это пар.
Эмульсионный режим
Этот режим потока обычно встречается в системах с высоким давлением и относительно высокими жидкостными нагрузками. Сдвигающее действие высокоскоростной жидкости «срывает» пузырьки пара, выходящие из отверстий на тарелке. Большая часть газа эмульгируется в виде мелких пузырьков внутри жидкости, при этом смесь ведет себя как однородная двухфазная жидкость, подчиняясь формуле Фрэнсиса Вейра. Это режим непрерывного течения жидкости.
Определение режима на лотке, приведенное ниже, носит информационный характер и не используется для определения размеров.
ii. Проверка перехода пена-эмульсия
Эта корреляция применима только для ситчатых тарелок.
Значение фактического параметра потока рассчитывается, как показано ниже:
, если значение фактического параметра.
III. Проверка перехода от пены к распылению:
Корреляция Портера и Дженкинса для перехода от пены к распылению.
, где,
LW — Длина водорослей в дюймах, B — активная площадь FT 2
P -PAGHT в дюймах
H . C9015
P -PANGE в дюймах
H . C 9014. C9015
P -PIGHT. дюймы
5. Унос:
Если унос чрезмерный, диаметр колонки или расстояние между тарелками обычно увеличивают. В качестве рекомендуемого значения унос из тарелки не должен превышать примерно 0,10 фунта жидкости, уносимой на фунт потока жидкости.
Методы определения уноса:
Корреляция уноса по ярмарке
Этот метод применим для пенного и эмульсионного режимов. Однако он менее точен для режима распыления. Для тарелок, работающих при высоком соотношении жидкости и пара, 0,1 фунта уносимой жидкости на фунт жидкости является избыточным количеством уносимой жидкости.
Однако он менее точен для режима распыления. Для тарелок, работающих при высоком соотношении жидкости и пара, 0,1 фунта уносимой жидкости на фунт жидкости является избыточным количеством уносимой жидкости.
Kister and Haas Correlation
Этот метод используется для режима распыления; Es — уносимый фунт жидкости/фунт пара.
7 мая 2012 г. в
Design Distillation System
Истинное положение – Допуск положения
Обозначение GD&T:
Определение:
Истинное положение, или просто положение, как его называет стандарт ASME Y14.5, определяется как общее допустимое отклонение, которое может иметь от своего «истинного» положения. « Истинное положение» — это точная координата или местоположение , определяемое базовыми размерами или другими способами, которые представляют номинальное значение. Другими словами, GD&T «Положение» Допуск — это то, насколько далеко местоположение вашего объекта может отличаться от его «Истинного положения» .
Позиция — один из самых полезных и сложных символов в GD&T. Два метода использования позиции, обсуждаемые на этой странице, будут RFS или независимо от размера элемента и в зависимости от существенного условия (максимальное материальное состояние или наименьшее существенное состояние). Однако, поскольку это такой полезный символ, мы продолжим добавлять контент и примеры для других применений этого изящного маленького символа в ближайшие месяцы.
Применение:
Несмотря на то, что это неверно, мы озаглавили эту страницу и иногда ссылаемся на символ как «Истинное положение», поскольку это обычно термин, на который ссылаются люди, когда ищут допуск положения. Однако в стандарте ASME Y14.5 это правильно называется просто «Позиция». Для ясности в отношении этих двух терминов ознакомьтесь с нашей статьей и видео здесь.
Позиция может быть применена к любому элементу размера (элементу с физическими размерами, например, отверстием, прорезью, бобышкой, выступом или сферой) и управлять центральными элементами этих элементов размера. См. приведенные выше центральные элементы отверстия, прорези и сферы. Расположение поверхностей должно контролироваться через профиль. Положение можно использовать с максимальным условием материала (MMC), минимальным состоянием материала (LMC), проекционными допусками и касательными плоскостями.
См. приведенные выше центральные элементы отверстия, прорези и сферы. Расположение поверхностей должно контролироваться через профиль. Положение можно использовать с максимальным условием материала (MMC), минимальным состоянием материала (LMC), проекционными допусками и касательными плоскостями.
На изображении ниже вы можете видеть, как отверстие обозначается с помощью символа допуска положения. Тем не менее, это также может быть применено к любому элементу размера, требующему допуска местоположения, например штифту, бобышке или даже шпоночному пазу. При наличии отверстия в детали, например в массиве болтов, обычно вызывается истинное положение. Его можно использовать практически везде, чтобы представляли объекты любого размера.
Положение относительно оси, точки или плоскости определяет, насколько объект может отличаться от заданного точного истинного положения. Опять же, True Position — это точное идеальное местоположение функции, расположена и ориентирована относительно базовой системы отсчета с помощью основных размеров .
Зона допуска положения
Допуск представляет собой трехмерную зону допуска, окружающую истинное положение. При указании допуска положения базовые элементы ссылаются на фрейм управления элементом. Это означает, что у вас будет точная точка, где положение должно быть относительно системы отсчета, и ваш допуск указывает, насколько далеко вы можете быть от нее. Положение чаще всего определяется двумя или тремя опорными элементами, чтобы точно определить и сориентировать истинное положение. Если элемент размера является цилиндрическим элементом, таким как отверстие в детали, значению размера в рамке управления элементом предшествует символ диаметра, представляющий круглую или цилиндрическую зону допуска.
Цилиндрическая зона допуска будет проходить через толщину детали, если это отверстие. Вся ось элементов, средняя плоскость или точка должны быть расположены в пределах этой зоны допуска.
Для измерения или проверки элемента, относящегося к управлению положением, можно выполнить измерения по осям X и Y элемента относительно опорных элементов, вызываемых в кадре управления элементом. Эти измерения можно быстро преобразовать в общее диаметральное отклонение. Если ваше диаметральное отклонение меньше указанного допуска, функция проходит. Помните, что для того, чтобы зафиксировать отклонения ориентации, необходимо будет выполнить несколько измерений по «глубине» отверстия или элемента.
Эти измерения можно быстро преобразовать в общее диаметральное отклонение. Если ваше диаметральное отклонение меньше указанного допуска, функция проходит. Помните, что для того, чтобы зафиксировать отклонения ориентации, необходимо будет выполнить несколько измерений по «глубине» отверстия или элемента.
В приведенном выше примере измеренное отклонение отверстия составляет 0,003 дюйма по оси X и 0,002 дюйма по оси Y. Используя приведенную формулу, расчетное отклонение диаметра составляет 0,007 дюйма. Заявленный позиционный допуск составляет 0,008 дюйма, поэтому деталь соответствует спецификации и может быть принята.
Положение с использованием модификатора состояния материала (MMC/LMC)
Положение элемента размера с MMC используется, когда функциональный датчик идеально подходит для проверки детали, обычно это используется, когда используется посадка с зазором с некоторыми своего рода застежка.
Если вы задаете элемент управления с помощью MMC, это позволяет допуску местоположения зависеть от размера элемента. Вы увидите положение, называемое MMC, очень часто в шаблонах болтов с зазором, где расположение всех болтов зависит от размера отверстия с зазором. LMC с положением немного менее распространен, но часто используется, когда требуется контролировать минимальную толщину стенки.
Вы увидите положение, называемое MMC, очень часто в шаблонах болтов с зазором, где расположение всех болтов зависит от размера отверстия с зазором. LMC с положением немного менее распространен, но часто используется, когда требуется контролировать минимальную толщину стенки.
Позиция, используемая с максимальным состоянием материала, становится очень полезным элементом управления. Положение в сочетании с допуском размера этого элемента может одновременно управлять положением, ориентацией, формой и размером элемента. Положение MMC полезно для создания функциональных датчиков, которые можно использовать для быстрой вставки в деталь, чтобы увидеть, все ли в пределах спецификации. В то время как допуск положения сам по себе определяет, насколько далеко от истинного положения может находиться элемент , независимо от размера элемента , position в сочетании с MMC задает минимальный размер и позиционное расположение отверстия для сохранения функционального контроля. Это позволяет позиции детали зависеть от фактического размера элемента. Это достигается путем добавления к детали бонусного допуска. По мере приближения детали к MMC ограничения становятся более жесткими, и отверстие должно быть ближе к ее положению. Но, если отверстие немного больше (но все еще соответствует спецификации), оно может еще больше отклониться от своего истинного положения и по-прежнему обеспечивать правильную работу (например, прохождение болта).
Это позволяет позиции детали зависеть от фактического размера элемента. Это достигается путем добавления к детали бонусного допуска. По мере приближения детали к MMC ограничения становятся более жесткими, и отверстие должно быть ближе к ее положению. Но, если отверстие немного больше (но все еще соответствует спецификации), оно может еще больше отклониться от своего истинного положения и по-прежнему обеспечивать правильную работу (например, прохождение болта).
Зона допуска такая же, как и выше, трехмерный цилиндр с центром в истинном положении, на которое ссылаются базовые поверхности. Цилиндрическая зона допуска будет проходить через толщину детали и будет различаться по диаметру в зависимости от допустимого дополнительного допуска по отношению к фактическому размеру элемента.
Бонусный раунд
Когда функциональный датчик используется для Позиции, любое отличие фактического размера элемента от максимального состояния материала будет дополнительным допуском. Бонусный допуск для положения затем увеличивается по мере приближения детали к LMC.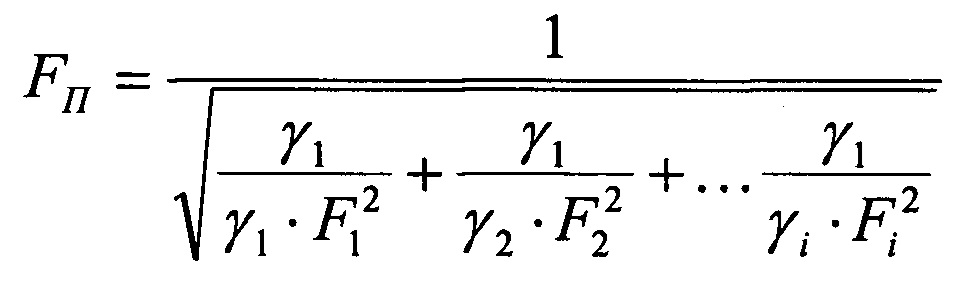 Цель выноски о максимальном состоянии материала состоит в том, чтобы гарантировать, что, когда деталь находится в наихудших допусках, Позиция и Размер отверстия/штифта всегда будет соответствовать. Например, если у вас был большой размер отверстия, но все еще был в допуске (ближе к LMC), вы увеличиваете бонусный допуск для себя, увеличивая допуск положения. Теперь центр отверстия может больше смещаться из-за дополнительного допуска.
Цель выноски о максимальном состоянии материала состоит в том, чтобы гарантировать, что, когда деталь находится в наихудших допусках, Позиция и Размер отверстия/штифта всегда будет соответствовать. Например, если у вас был большой размер отверстия, но все еще был в допуске (ближе к LMC), вы увеличиваете бонусный допуск для себя, увеличивая допуск положения. Теперь центр отверстия может больше смещаться из-за дополнительного допуска.
Бонусный допуск = (измеренный размер отверстия – размер отверстия MMC)
Примечание. Имейте в виду, что обратное верно для положительного элемента, такого как штифт, где меньше булавка означает, что у вас больше бонусной терпимости.
Когда деталь проверяется на предмет положения под элементом спецификации размера, обычно используется функциональный датчик, чтобы убедиться, что вся область функции находится в пределах спецификации. По сути, это моделирование наихудшего сценария границы сопрягаемых частей. Если у вас есть спецификация для максимального состояния материала, желаемое состояние заключается в том, что поверхность элемента не будет пересекать функциональную оболочку, известную как виртуальное состояние. Для MMC на отверстии это обычно означает границу «наихудшего сценария», при которой сборка еще возможна. Следующие формулы используются для создания датчика положения в MMC.
Если у вас есть спецификация для максимального состояния материала, желаемое состояние заключается в том, что поверхность элемента не будет пересекать функциональную оболочку, известную как виртуальное состояние. Для MMC на отверстии это обычно означает границу «наихудшего сценария», при которой сборка еще возможна. Следующие формулы используются для создания датчика положения в MMC.
Фиксированное измерение внутреннего элемента
Для истинного положения под MMC отверстия :
Калибр Ø (штифт) = Мин. Ø отверстия (MMC) — Допуск истинного положения
Фиксированный калибр
Для положения под MMC штифта :
Калибр Ø (калибр отверстия) = Макс. Ø штифта (MMC) + Допуск истинного положения даны на чертеже в качестве основных размеров. Все элементы датчика должны быть расположены в истинных позициях, но размеры должны соответствовать приведенным выше формулам.
Помните, что чем дальше вы находитесь от MMC, когда на нее ссылаются в рамке управления функцией, тем больше бонусных допусков вам разрешено. Для отверстия, чем больше диаметр (ближе к LMC), тем больше дополнительный допуск для вашего истинного положения.
Для отверстия, чем больше диаметр (ближе к LMC), тем больше дополнительный допуск для вашего истинного положения.
Вызывается с символом Ø или без него.
Позиция может быть вызвана двумя способами: либо как расстояние, по осям X и Y, либо, чаще всего, как диаметр. Когда положение вызывается как расстояние, вам разрешается отойти от допуска в направлении X или Y на разрешенный допуск. Однако в этом случае зона допуска образует квадрат. Это обычно нежелательно, так как углы квадрата дальше от центра, чем стороны. Это также удалило более 57% вашей зоны толерантности! Чаще всего положение относительно местоположения обозначается символом диаметра (Ø), который называется цилиндрической или круглой зоной допуска.
Запутались? Без проблем! Для получения более подробной информации о том, как бонусные допуски влияют на эти выноски, см. разделы Максимальное состояние материала . Или ознакомьтесь с нашим курсом GD&T , где мы подробно рассмотрим символ позиции!
Связь с другими символами GD&T:
Символ положения является позиционным символом для GD&T. Он находит особенности размера, а также контролирует ориентацию. В сочетании с допуском размера этого элемента они управляют размером, местоположением, ориентацией и формой. Однако он не может управлять расположением поверхностей, где вступает в действие профиль поверхности. Он действует так же, как и положение, однако он может управлять расположением, ориентацией и формой элементов поверхности.
Он находит особенности размера, а также контролирует ориентацию. В сочетании с допуском размера этого элемента они управляют размером, местоположением, ориентацией и формой. Однако он не может управлять расположением поверхностей, где вступает в действие профиль поверхности. Он действует так же, как и положение, однако он может управлять расположением, ориентацией и формой элементов поверхности.
Истинное положение управляет ориентацией, что означает, что оно уже управляет элементом так же, как Перпендикулярность, Параллелизм и Угловатость. Допуск как положения, так и этих элементов управления ориентацией относится к цилиндрической оболочке центральной оси. Однако с истинным положением вы можете сделать допуск привязанным к нескольким базам, а не только к одной с перпендикулярностью оси, таким образом, также контролируя местоположение. Когда вы указываете истинное положение с помощью баз на грани и сторонах детали, также контролируется перпендикулярность.
Специальные примечания:
Вот пример урока из нашего курса «Основы GD&T». Мы объясняем, почему гораздо лучше использовать допуск положения и базовые размеры, а не размещать объект с помощью системы координатных размеров.
Мы объясняем, почему гораздо лучше использовать допуск положения и базовые размеры, а не размещать объект с помощью системы координатных размеров.
Позиция, вероятно, является наиболее широко используемым символом в GD&T. Если вам нужна дополнительная информация о позиции или любых других символах, вам следует ознакомиться с нашим курсом по основам GD&T. Если вам нравится упрощенный подход к GD&T на этом веб-сайте и в видео выше, обязательно свяжитесь с нами, чтобы узнать больше о курсе!
Станьте ведущим инженером в своей компании
Изучайте GD&T в удобном для вас темпе и уверенно применяйте их в реальном мире.
Пройти обучение GD&T
Все символы
Физики впервые экспериментально подтвердили теорему Хокинга о черной дыре | MIT News
Существуют определенные правила, которым должны подчиняться даже самые экстремальные объекты во Вселенной. Центральный закон для черных дыр предсказывает, что площадь их горизонта событий — граница, за которую ничто не может выйти — никогда не должна уменьшаться. Этот закон — теорема площадей Хокинга, названная в честь физика Стивена Хокинга, который вывел теорему в 1971.
Центральный закон для черных дыр предсказывает, что площадь их горизонта событий — граница, за которую ничто не может выйти — никогда не должна уменьшаться. Этот закон — теорема площадей Хокинга, названная в честь физика Стивена Хокинга, который вывел теорему в 1971.
Пятьдесят лет спустя физики из Массачусетского технологического института и других организаций впервые подтвердили теорему Хокинга о площади, используя наблюдения гравитационных волн. Их результаты опубликованы сегодня в Physical Review Letters .
В ходе исследования исследователи более внимательно изучили GW150914, первый сигнал гравитационных волн, обнаруженный Лазерной интерферометрической гравитационно-волновой обсерваторией (LIGO) в 2015 году. черная дыра вместе с огромным количеством энергии, которая пульсирует в пространстве-времени в виде гравитационных волн.
Если теорема Хокинга о площади верна, то площадь горизонта новой черной дыры не должна быть меньше общей площади горизонта ее родительских черных дыр. В новом исследовании физики повторно проанализировали сигнал от GW150914 до и после космического столкновения и обнаружили, что действительно общая площадь горизонта событий не уменьшилась после слияния — результат, о котором они сообщают с 95-процентной достоверностью.
В новом исследовании физики повторно проанализировали сигнал от GW150914 до и после космического столкновения и обнаружили, что действительно общая площадь горизонта событий не уменьшилась после слияния — результат, о котором они сообщают с 95-процентной достоверностью.
Их результаты знаменуют собой первое прямое наблюдательное подтверждение теоремы Хокинга о площади, которая была доказана математически, но до сих пор никогда не наблюдалась в природе. Команда планирует протестировать будущие сигналы гравитационных волн, чтобы увидеть, могут ли они еще больше подтвердить теорему Хокинга или стать признаком новой, законопослушной физики.
«Возможно, что существует целый зоопарк различных компактных объектов, и хотя некоторые из них являются черными дырами, которые следуют законам Эйнштейна и Хокинга, другие могут быть немного другими существами», — говорит ведущий автор Максимилиано Иси, научный сотрудник NASA Einstein Postdoctoral Fellow. в Институте астрофизики и космических исследований им. Кавли Массачусетского технологического института. «Итак, это не значит, что вы делаете этот тест один раз, и он закончен. Вы делаете это один раз, и это начало».
Кавли Массачусетского технологического института. «Итак, это не значит, что вы делаете этот тест один раз, и он закончен. Вы делаете это один раз, и это начало».
Соавторами Иси по статье являются Уилл Фарр из Университета Стоуни-Брук и Центра вычислительной астрофизики Института Флэтайрон, Мэтью Гислер из Корнельского университета, Марк Шил из Калифорнийского технологического института и Сол Теукольски из Корнельского университета и Калифорнийского технологического института.
Эпоха прозрений
В 1971 году Стивен Хокинг предложил теорему площадей, которая положила начало серии фундаментальных открытий о механике черных дыр. Теорема предсказывает, что общая площадь горизонта событий черной дыры — и всех черных дыр во Вселенной, если уж на то пошло — никогда не должна уменьшаться. Это утверждение было любопытной параллелью второму закону термодинамики, утверждающему, что энтропия, или степень беспорядка внутри объекта, также никогда не должна уменьшаться.
Сходство между двумя теориями предполагало, что черные дыры могут вести себя как термальные, излучающие тепло объекты — сбивающее с толку предположение, поскольку считалось, что черные дыры по самой своей природе никогда не пропускают энергию или излучают. В конце концов Хокинг сопоставил две идеи в 1974 году, показав, что черные дыры могут иметь энтропию и излучать излучение в течение очень длительного времени, если принять во внимание их квантовые эффекты. Это явление получило название «излучение Хокинга» и остается одним из самых фундаментальных открытий о черных дырах.
«Все началось с осознания Хокингом того, что общая площадь горизонта черных дыр никогда не может уменьшиться, — говорит Иси. «Закон о зонах воплощает в себе золотой век 70-х годов, когда все эти идеи были получены».
Хокинг и другие с тех пор показали, что теорема площади работает математически, но не было никакого способа проверить ее на природе до первого обнаружения LIGO гравитационных волн.
Хокинг, узнав о результате, быстро связался с соучредителем LIGO Кипом Торном, профессором теоретической физики Фейнмана в Калифорнийском технологическом институте. Его вопрос: может ли обнаружение подтвердить теорему площадей?
В то время у исследователей не было возможности выделить в сигнале необходимую информацию до и после слияния, чтобы определить, не уменьшилась ли конечная площадь горизонта, как предполагала теорема Хокинга. Только несколько лет спустя Иси и его коллеги разработали методику, когда проверка закона площадей стала возможной.
До и после
В 2019 году Иси и его коллеги разработали метод извлечения реверберации сразу после GW1509Пик 14 — момент, когда две родительские черные дыры столкнулись, образовав новую черную дыру. Команда использовала эту технику, чтобы выбрать определенные частоты или тона шумных последствий, которые они могли использовать для расчета окончательной массы и вращения черной дыры.
Масса и вращение черной дыры напрямую связаны с площадью ее горизонта событий, и Торн, вспомнив вопрос Хокинга, обратился к ним с вопросом: могут ли они использовать один и тот же метод для сравнения сигнала до и после слияния? и подтвердить теорему площади?
Исследователи приняли вызов и снова разделили сигнал GW150914 на его пике.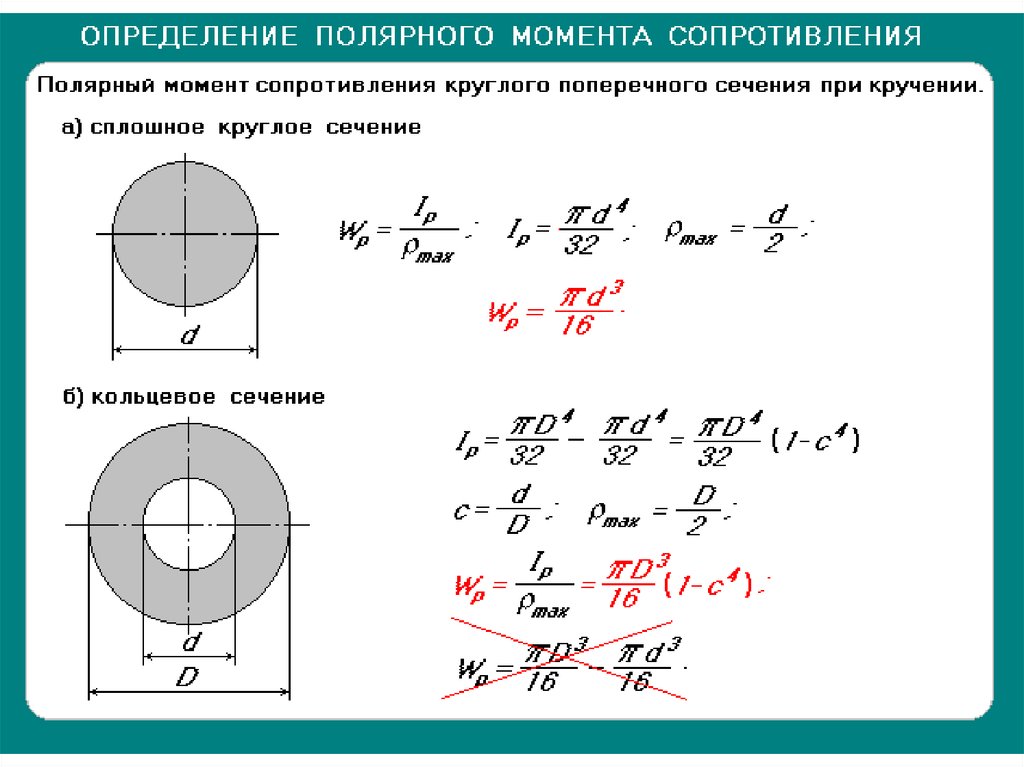 Они разработали модель для анализа сигнала до пика, соответствующего двум вдохновляющим черным дырам, и для определения массы и вращения обеих черных дыр до их слияния. Исходя из этих оценок, они рассчитали общую площадь горизонта — примерно 235 000 квадратных километров, или примерно в девять раз больше площади Массачусетса.
Они разработали модель для анализа сигнала до пика, соответствующего двум вдохновляющим черным дырам, и для определения массы и вращения обеих черных дыр до их слияния. Исходя из этих оценок, они рассчитали общую площадь горизонта — примерно 235 000 квадратных километров, или примерно в девять раз больше площади Массачусетса.
Затем они использовали свою предыдущую технику для извлечения «кольца» или реверберации вновь образованной черной дыры, на основании чего они рассчитали ее массу и вращение, а в конечном итоге площадь ее горизонта, которая, как они обнаружили, была эквивалентна 367 000 квадратных километров (приблизительно в 13 раз больше площади штата Бэй).
«Данные с подавляющей уверенностью показывают, что площадь горизонта увеличилась после слияния и что закон площадей выполняется с очень высокой вероятностью», — говорит Иси. «Было облегчением то, что наш результат действительно согласуется с парадигмой, которую мы ожидаем, и подтверждает наше понимание этих сложных слияний черных дыр».
Команда планирует продолжить проверку теоремы Хокинга о площади и других давних теорий механики черных дыр, используя данные LIGO и Virgo, ее аналога в Италии.
«Обнадеживает то, что мы можем по-новому, творчески подойти к анализу данных о гравитационных волнах и ответить на вопросы, на которые раньше не могли ответить, — говорит Иси. «Мы можем продолжать дразнить фрагменты информации, которые напрямую связаны с основами того, что, как мы думаем, мы понимаем. Однажды эти данные могут раскрыть то, чего мы не ожидали».
Это исследование было частично поддержано НАСА, Фондом Саймонса и Национальным научным фондом.
Поделиться этой новостной статьей:
Бумага
Документ: «Проверка закона площади черной дыры с помощью GW150914»
Упоминания в прессе
Popular Mechanics
Исследователи из Массачусетского технологического института и других учреждений смогли экспериментально подтвердить одну из теорем Стивена Хокинга о черных дырах, измеряя гравитационные волны до и после слияния черных дыр, чтобы предоставить доказательства того, что горизонт событий черной дыры никогда не может сузиться, сообщает Кэролайн Делберт для Popular Mechanics . «Этот классный анализ не просто показывает пример теоремы Хокинга, лежащей в основе одного из центральных законов, влияющих на черные дыры, — пишет Делберт, — он показывает, как анализ моделей гравитационных волн может подтверждать статистические результаты».
«Этот классный анализ не просто показывает пример теоремы Хокинга, лежащей в основе одного из центральных законов, влияющих на черные дыры, — пишет Делберт, — он показывает, как анализ моделей гравитационных волн может подтверждать статистические результаты».
Full story via Popular Mechanics →
- Maximiliano Isi
- MIT Kavli Institute for Astrophysics and Space Research
- LIGO Laboratory
- Department of Physics
- School of Science
What’s the Difference Between Bearing, Напряжение сдвига и отрыва?
Загрузить эту статью в формате .PDF
Соединение является основной функцией проектирования. Например, при соединении двух деталей болтами могут учитываться свойства материала и силы нагрузки. Здесь мы сосредоточимся на предварительном натяге, сдвиге и отрыве болтового соединения. Тем не менее, проектировщики должны учитывать несколько инженерных принципов, включая внутренние и внешние нагрузки, которые обсуждались в ряде статей по 9Веб-сайт компании 3599 Machine Design.
Инженеры, возможно, узнали об этих напряжениях в школе, но одним из факторов, усложняющих то, что может показаться простым болтовым соединением, является усилие зажима или предварительная нагрузка. Для расчета соединений без предварительного натяга можно использовать стандартные формулы сдвига и подшипников, описанные далее в этой статье. Однако предварительная нагрузка часто является фактором усталостной долговечности сустава; он создает растягивающие усилия и может способствовать ползучести.
Важно рассчитать правильную площадь. В зависимости от конструкции штифтовое или болтовое соединение может распределять нагрузку по нескольким поверхностям. На втором изображении нагрузка будет распределяться по удвоенной площади.
В жесткой сборке предварительная нагрузка выше, чем рабочая нагрузка, поэтому рабочая нагрузка будет или должна оказывать незначительное влияние на силы натяжения крепежа. Это уменьшает усталостное разрушение, даже когда применяется динамическая переменная нагрузка. Это применимо только в том случае, если проектировщик учел разницу прочности на растяжение и предела выносливости крепежного изделия. Циклическая нагрузка на соединение будет рассчитана на предел выносливости, а не на предел прочности крепежного элемента. Например, если крепеж имеет минимальную прочность на растяжение около 150 тысяч фунтов, а предел выносливости составляет 15 тысяч фунтов, соединение при циклической нагрузке не сможет превысить 15 тысяч фунтов или может преждевременно выйти из строя из-за усталости.
Это применимо только в том случае, если проектировщик учел разницу прочности на растяжение и предела выносливости крепежного изделия. Циклическая нагрузка на соединение будет рассчитана на предел выносливости, а не на предел прочности крепежного элемента. Например, если крепеж имеет минимальную прочность на растяжение около 150 тысяч фунтов, а предел выносливости составляет 15 тысяч фунтов, соединение при циклической нагрузке не сможет превысить 15 тысяч фунтов или может преждевременно выйти из строя из-за усталости.
Согласно техническому меморандуму по определению нагрузки на болты, опубликованному НАСА, болты обычно должны создавать зажимное усилие, которое при правильном расчете будет воспринимать менее 20% внешних нагрузок на болты. Большая часть работы выполняется за счет энергии сжатия, возникающей на фланцах при затягивании болтов.
На предварительную нагрузку влияют многие переменные, в том числе предел прочности при растяжении, отделка, форма головки и смазка. Смазочные материалы снижают крутящий момент, необходимый для создания зажимного усилия. Покрытия могут уменьшить или увеличить требуемый крутящий момент. Умножение стандартного крутящего момента всухую на целых 0,45–1,70 может компенсировать смазку и покрытие. Например, молибденовая смазка, пленка и паста могут снизить крутящий момент, необходимый для создания надлежащего усилия зажима, на 30%, 40% или 45% соответственно. К сожалению, не существует простого и абсолютно надежного способа рассчитать точную предварительную нагрузку, необходимую для каждого применения (дополнительную информацию см. в разделе «Расчет правильной предварительной нагрузки для резьбовых креплений»). Такие факторы, как головка болта, тип резьбы, шайба и крепежные пластины, также помогают увеличить площадь поверхности, чтобы предотвратить проскальзывание, которое приведет к уменьшению предварительного натяга и потенциально может вызвать проскальзывание или привести к другому виду отказа. Существуют стандарты, которые также могут помочь вам в предварительном натягивании креплений.
Смазочные материалы снижают крутящий момент, необходимый для создания зажимного усилия. Покрытия могут уменьшить или увеличить требуемый крутящий момент. Умножение стандартного крутящего момента всухую на целых 0,45–1,70 может компенсировать смазку и покрытие. Например, молибденовая смазка, пленка и паста могут снизить крутящий момент, необходимый для создания надлежащего усилия зажима, на 30%, 40% или 45% соответственно. К сожалению, не существует простого и абсолютно надежного способа рассчитать точную предварительную нагрузку, необходимую для каждого применения (дополнительную информацию см. в разделе «Расчет правильной предварительной нагрузки для резьбовых креплений»). Такие факторы, как головка болта, тип резьбы, шайба и крепежные пластины, также помогают увеличить площадь поверхности, чтобы предотвратить проскальзывание, которое приведет к уменьшению предварительного натяга и потенциально может вызвать проскальзывание или привести к другому виду отказа. Существуют стандарты, которые также могут помочь вам в предварительном натягивании креплений. Однако это не быстрое решение, поскольку каждый стандарт фокусируется на отдельном приложении или технологии. ASTM, ANIS, ASME, IOS и другие могут перекрываться, в то время как другие могут иметь пробелы между ними.
Однако это не быстрое решение, поскольку каждый стандарт фокусируется на отдельном приложении или технологии. ASTM, ANIS, ASME, IOS и другие могут перекрываться, в то время как другие могут иметь пробелы между ними.
Спецификации ASTM для высокопрочных болтов A325 и A490 должны быть натянуты до 70% от минимального предела прочности на растяжение. В приведенной выше таблице показано это минимальное предварительное натяжение болтов для эмпирических размеров болтов. Процент может варьироваться, но это корректировка в зависимости от предела текучести смещения материала. Для жестких стальных деталей основное указание, данное в Справочнике механика, заключается в том, чтобы затянуть крепежные детали до 75% смещения предела текучести или условного предела текучести. Меньшие крутящие моменты следует учитывать для гибких соединений — соединений с прокладками или узлов, подверженных воздействию высоких температур.
Федеральное авиационное управление предлагает следующий пример: «Усилие зажима, создаваемое правильно натянутым крепежным элементом, обычно составляет около 75 % испытательной нагрузки. Испытательная нагрузка болта SAE J429 Grade 2 составляет 4250 фунтов. Результирующее усилие зажима:
Испытательная нагрузка болта SAE J429 Grade 2 составляет 4250 фунтов. Результирующее усилие зажима:
4250 * 0,75 = 3187,5 фунта.
Величина крутящего момента, необходимая для достижения этой нагрузки, приблизительно равна:
T = K*D*Fp
где:
T = крутящий момент болта в дюйм-фунтах
K = коэффициент трения (безразмерный)
D = номинальный диаметр болта (дюймы)
Fp = осевое усилие зажима (фунты)
Подстановка чисел в уравнение:
T = 0,2 * 0,375 * 3188 = 239,1 дюйма фунтов или примерно 20 фут-фунтов.
Таким образом, сухой болт SAE Grade 2 должен быть затянут примерно с усилием 20 футо-фунтов. для достижения силы зажима 3188 фунтов. Однако в Техническом меморандуме НАСА упоминается, что болты могут составлять от 65% до 90% предела текучести материала. Опять же, это показывает, что диапазон болтового соединения может варьироваться в зависимости от применения, коэффициента безопасности, стандартов и того, насколько вы консервативны в расчетах. По данным НАСА, в целом также можно с уверенностью предположить, что погрешность для ручных динамометрических ключей на смазанных крепежных элементах составляет +/- 25%. Однако при использовании прибора для измерения нагрузки фактор неопределенности предварительной нагрузки может быть уменьшен до +/- 5 %.
По данным НАСА, в целом также можно с уверенностью предположить, что погрешность для ручных динамометрических ключей на смазанных крепежных элементах составляет +/- 25%. Однако при использовании прибора для измерения нагрузки фактор неопределенности предварительной нагрузки может быть уменьшен до +/- 5 %.
Напряжение подшипника
Свойства подшипника — это силы, действующие на отверстие, через которое проходит болт. Испытание на подшипник должно определить, может ли быть какая-либо деформация отверстия. Предварительное нагружение снижает усилия смятия, но не все болтовые соединения предварительно нагружены. Чтобы рассчитать напряжение смятия, разделите усилие на площадь контакта между крепежным элементом и отверстием. Теоретически часто это простая площадь опорной поверхности.
δ б =P/A б
Где …
δ b = опорная сила
P = осевые силы, действующие на крепеж или пластину
A b = опорная поверхность длина контактной площадки, умноженная на диаметр отверстия. Если есть зазор, то более точным будет умножение ответа на число Пи, деленное на четыре. Ни одно из этих уравнений не учитывает, что напряжение не распределяется равномерно по диаметру отверстия. Распределение напряжения ближе к эллипсу с большей силой в направлении осевой силы. Добавление большего количества креплений снижает нагрузку на опору за счет увеличения площади нескольких отверстий.
Если есть зазор, то более точным будет умножение ответа на число Пи, деленное на четыре. Ни одно из этих уравнений не учитывает, что напряжение не распределяется равномерно по диаметру отверстия. Распределение напряжения ближе к эллипсу с большей силой в направлении осевой силы. Добавление большего количества креплений снижает нагрузку на опору за счет увеличения площади нескольких отверстий.
Расчет отрыва аналогичен другим уравнениям напряжения (сила, деленная на площадь). Однако, в отличие от некоторых других, вы можете выбрать, в какой точке рассчитывать площадь. Область отрыва иногда берут от центра отверстия под болт к внешней стороне материала, увеличивая площадь на радиус отверстия. Более консервативный подход состоит в том, чтобы взять область от края отверстия под болт до края материала.
Напряжение сдвига
Для болтовых соединений без предварительного напряжения сдвига напряжение рассчитывается как напряжение смятия: сила по площади. Как и напряжение подшипника, это также среднее напряжение, и максимальный сдвиг будет выше. Если болтовое соединение не имеет разделения или зазора, может возникнуть ситуация прямого сдвига — сдвига без изгиба.
Как и напряжение подшипника, это также среднее напряжение, и максимальный сдвиг будет выше. Если болтовое соединение не имеет разделения или зазора, может возникнуть ситуация прямого сдвига — сдвига без изгиба.
τ = V/A сдвиг
где:
τ = напряжение сдвига
V = усилие
A сдвиг = площадь сдвига
прямое напряжение сдвига устраняет идеалы, так как они уменьшают внешние напряжения и уменьшают их. проскальзывание. Однако даже предварительно нагруженные соединения могут подвергаться чрезмерным нагрузкам, ударным нагрузкам или ползучести, которые уменьшают предварительную нагрузку и могут вызвать сдвиг при изгибе. Иногда называемая поперечной нагрузкой, она определяется, как правило, заранее полученным уравнением:
Это все еще упрощенный способ проектирования болтового соединения. Имейте в виду, что важно понимать все потенциальные нагрузки и то, как они будут действовать на суставы. Изгибающее напряжение на балке может увеличить растягивающие и сдвигающие напряжения на болтах. (Способ визуализировать изгиб балки см. в разделе «В чем разница между диаграммами балки?».) срезать материал, окружающий отверстие.Для предотвращения отрыва рекомендуется, чтобы расстояние от края материала до края отверстия было равно, по крайней мере, диаметру отверстия.Соотношение диаметра края к диаметру отверстия находится в диапазоне от 1,5 до 2,0 являются общими.
(Способ визуализировать изгиб балки см. в разделе «В чем разница между диаграммами балки?».) срезать материал, окружающий отверстие.Для предотвращения отрыва рекомендуется, чтобы расстояние от края материала до края отверстия было равно, по крайней мере, диаметру отверстия.Соотношение диаметра края к диаметру отверстия находится в диапазоне от 1,5 до 2,0 являются общими.
AISC J3.4 примерно следует коэффициенту 1,5, где AISC J3.5 указывает, что расстояние от отверстия под болт до края материала должно быть в 12 раз больше толщины соединяемой детали, но не более 6 дюймов. Для расстояние между болтовыми отверстиями равно 24-кратной толщине более тонкого корпуса/детали, но не более 12 дюймов.
Концентрации напряжений могут рассеяться относительно быстро, но расстояние до края материала или другая концентрация напряжений могут вызвать напряжения отрыва. То же самое отношение края к отверстию также может дать представление о расстоянии между отверстиями для болтов. Для компании важно определить, каким стандартам и уравнениям должны следовать инженеры, чтобы соединения проектировались единообразно и сводились к минимуму вариации. В Интернете есть ресурсы, такие как калькуляторы расстояний. В идеале они должны показывать, как они рассчитываются или каким стандартам они следуют. Если нет, просто используйте их в качестве оценок или чего-то, с чем можно сверить свою работу.
Для компании важно определить, каким стандартам и уравнениям должны следовать инженеры, чтобы соединения проектировались единообразно и сводились к минимуму вариации. В Интернете есть ресурсы, такие как калькуляторы расстояний. В идеале они должны показывать, как они рассчитываются или каким стандартам они следуют. Если нет, просто используйте их в качестве оценок или чего-то, с чем можно сверить свою работу.
Запас прочности
Коэффициент безопасности будет изменяться в зависимости от натяжения крепежных деталей, прочности материала и т. д. Использование предварительной нагрузки уменьшит усилия сдвига и опоры, поскольку движение в соединении уменьшается за счет сил трения или сжатия. (Чтобы узнать больше о том, как внешние нагрузки влияют на упругий центр крепежа, см. раздел «Как группы болтов реагируют на внешние нагрузки».)
Коэффициент безопасности и запас прочности можно изменить, чтобы обеспечить предварительную нагрузку. Обратите внимание, что эта нормальная сила изменит запас прочности. Существует множество уравнений для коэффициентов безопасности и запасов прочности. Ниже показано, что допустимые напряжения обычно делятся на фактические напряжения. Если вы проектируете что-то легкое, а запас прочности близок к нулю, но вы не учли предварительную нагрузку, в стыке может не хватать запаса прочности.
Существует множество уравнений для коэффициентов безопасности и запасов прочности. Ниже показано, что допустимые напряжения обычно делятся на фактические напряжения. Если вы проектируете что-то легкое, а запас прочности близок к нулю, но вы не учли предварительную нагрузку, в стыке может не хватать запаса прочности.
мс = ( T A /P B ) -1
Где:
MS = Маржинал
T A 2 = TINSABLE
T 00 A 2 = TINSABLE
T 00 A 2 = TINSABLE
T 00 A 2 = TIENBLEABLE
= Суммарная осевая нагрузка на болт
Для обеспечения запаса прочности на сдвиг просто поменяйте местами растягивающую и осевую нагрузку на сдвиг. Для комбинированного изгиба и сдвига можно оставить:
где:
R b = Суммарная допустимая осевая нагрузка на болт/изгиб
R τ = (Коэффициент запаса прочности*сила)/допустимый сдвиг
Некоторые расчеты будут включать значение предварительного натяга, где сила растяжения болтов умножается на сумму квадратного корня из силы сдвига и силы изгиба.
