Решение.
Обозначим квадраты буквами так, как показано на рисунке. Перенесём мысленно часть озера, находящуюся в квадрате D, в квадрат А. Сумма этих площадей меньше половины площади квадрата. Площадь части озера в квадрате С примерно половина площади квадрата, другая половина пустая — перенесем в неё части озера из А и D вместе взятые. Этим квадрат С будет заполнен. Теперь перенесём часть озера, лежащую ниже диагонали квадрата Е, на незанятую часть в квадрате F. Теперь квадрат F заполнен почти полностью, а квадрат Е заполнен наполовину. Итак, озеро покрывает приблизительно два полных квадрата С и F, почти полный квадрат В и половину квадрата Е. Значит, площадь озера больше 3 кв. км, но меньше 3,5 кв. км. Округляя, получаем 3 кв. км.
Ответ: 3.
Примечание редакции Решу ЕГЭ.
Понимая необходимость умений проводить подобные оценки и прикидки в прикладных науках, все же отметим, что приведённые выше рассуждения не имеют никакого отношения к математике. Почему? Потому, что нет доказательств. Например, того, часть из Е действительно поместится в F. Доказательство можно было бы провести так: наложить карту на миллиметровку, найти количество квадратиков, в которые попала фигура, и точно установить границы, в которых лежит площадь: отбросив частично заполненные квадратики, получим площадь с недостатком, учитывая все частично заполненные квадратики, найдем площадь с избытком. Но это путь не для экзамена.
Примечание Д. Д. Гущина о применении палетки для определения площади.
Читательница Ольга Кулешова рассказала нам, что в начальных классах изучают способ нахождения площади фигуры с помощью палетки (квадратной сетки). Площадь фигуры считается равной количеству полностью заполненных клеток сетки плюс половина количества не полностью заполненных клеток. Решая данную задачу таким способом, найдем, что количество полностью заполненных клеток равно 0, количество частично заполненных клеток равно 6, следовательно, площадь фигуры равна 0 + 6 : 2 = 3.
Об этом необходимо сказать следующее.
Для фигур случайной формы, покрытых большим количеством клеток, указанное приближение площади нередко дает удовлетворительную точность. Однако в ряде случаев погрешность становится неприемлемой.
Найдем, к примеру, указанным методом площадь изображенных на рисунке круга и пятиугольника. Для круга сложим 5 целых клеток и половину от 16 частично заполненных, вместе 13 клеток. Как нетрудно проверить, используя формулу для площади круга найденная по клеточкам площадь круга мало отличается от расчетной. Но найдем теперь площадь пятиугольника: к 6 целым клеткам прибавим половину от 9, получим 10,5 или, округленно, 11 клеток. Однако в действительности площадь пятиугольника не 11 и даже не 10, а меньше 9 клеток. Ошибка превосходит 17%, а после округления — даже 22%.
По всей вероятности, точной формулы для оценки погрешности использования квадратной палетки при оценке площади не существует. Но ясно, что погрешность может быть достаточно велика, если все частично заполненные клетки заполнены более (либо менее), чем наполовину, или если покрывающих фигуру клеток слишком мало.
В приведенном выше задании ЕГЭ площадь покрыта всего шестью клетками. В таких случаях найденный ответ может получиться верным, но может оказаться и ошибочным. Поэтому на экзамене пользоваться указанным методом нельзя. Однако метод можно усовершенствовать. Об этом ниже.
Подробнее прочитать о приближенном определении площадей можно, например, в учебном пособии для высших учебных заведений Инженерная геодезия.pdf.
Примечание Т. Н. Кравченко о последовательных приближениях при применении палетки.
Укажем путь, которым можно находить все более точное значение площади, применяя палетки с уменьшающимся шагом сетки. Истинная площадь фигуры не меньше площади полностью закрашенных клеток. Добавляя к ней половину площади частично закрашенных клеток, мы можем получить избыток или недостаток. Если все частично заполненные клетки «почти пустые», мы получим избыток, равный половине их суммарной площади. Если же все эти клетки «почти полные», площадь будет определена с недостатком, равным половине их суммарной площади. В обоих случаях погрешность площади не больше где n — количество частично закрашенных клеток, S — площадь одной клетки. Теперь ясно, что можно попытаться уменьшить погрешность, последовательно уменьшая шаг сетки. Продемонстрируем это на примере нашей задачи.
Рис. 1.
Рис. 2.
Рис. 3.
Рис. 4.
Изначально площадь одной клетки равна 1. По первому рисунку видно, что озеро Великое расположено в 6 клетках, и ни одна из них не заполнена полностью. В первом приближении площадь озера равна Погрешность в этом случае также равна 3. Поэтому необходимо уменьшить погрешность.
Разделим каждую клетку пополам по вертикали и горизонтали (см. рис. 2), то есть на 4 части. Площадь каждой получившейся клетки теперь равна Озеро Великое занимает 5 клеток целиком, и 14 клеток заполнены не полностью. Следовательно, во втором приближении площадь озера составляет
при этом погрешность равна
что нас также не устраивает.
На третьем шаге снова разделим все клетки пополам по вертикали и горизонтали, то есть на 4 части (см. рис. 3). Площадь каждой получившейся клетки будет равна Теперь озеро Великое занимает 36 клеток полностью, и еще 28 клеток заполнены не полностью. Площадь озера составляет
при этом погрешность равна Сделаем еще одно разбиение.
Снова разделим все клетки пополам по вертикали и горизонтали. Площадь каждой получившейся клетки будет равна Теперь озеро Великое занимает 172 клетки полностью, и еще 52 клетки заполнены частично. Площадь озера составляет
при этом погрешность равна Таким образом, площадь озера больше 2,5. Наибольшее значение площади равно
Это значение достигается, если все частично заполненные клетки заполнены полностью. Но это не так, а потому площадь меньше 3,5. Тем самым строго доказано, что округленное до целых значение площади равно 3.
Подсчитывать количество полностью и не полностью заполненных клеток может быть утомительно. Для облегчения работы можно делить на части только те клетки, которые заполнены не полностью. Покажем это ниже.
По пятому рисунку 5 видно, что озеро не занимает целиком ни одной клетки. Разделим каждую из частично заполненных клеток на четыре части (см. рис. 6). Среди получившихся маленьких клеток полностью заполнено 5 клеток (выделено синим), а еще несколько клеток заполнены не полностью.
Еще раз разделим каждую из частично заполненных клеток на четыре части (см. рис. 7). Среди получившихся маленьких клеток полностью заполнено 16 (выделено желтым), и еще 30 клеток заполнены не полностью. Таким образом, на третьем шаге озеро занимает: 5 целых клеток площадью каждая; 16 3целых клеток площадью
каждая и 30 частично заполненных клеток площадью
каждая. Найдем площадь озера на этом шаге:
Погрешность определяется последним слагаемым, равным 0,9375, то есть площадь озера может оказаться и меньше 2,5, и больше 3,5, а тогда округление до целых даст 2 или 4 соответственно. Необходим дальше уменьшать шаг сетки.
Еще раз разделим каждую из частично заполненных клеток на четыре части (см. последний рисунок). Теперь озеро занимает: 5 целых клеток площадью 16 целых клеток площадью
29 целых клеток площадью
и 62 частично заполненные клетки площадью
Находим площадь озера:
Погрешность определяется последним слагаемым, равным 0,484375. Следовательно, площадь озера больше 2,5, и округление до 2 невозможно. Оценка сверху дает 3,671875, то есть площадь может оказаться больше 3,5, а тогда понадобится округление до 4. Так случилось бы, если бы все 62 частично заполненные на последнем шаге клетки были бы заполнены почти полностью. Но это не так. Поэтому на данном шаге можно предположить, что площадь не превзойдет 3,5, а потому должна быть округлена до 3.
Вычисление площади по формуле для ряда фигур дает сильно завышенную погрешность, поэтому для большинства экзаменационных задач, в отличие от этой, нахождение площади применением палеток с уменьшающимся шагом сетки обычно дает хороший результат при однократном делении исходных клеток на 4 части по вертикали и горизонтали, то есть всего на 16 частей.
Такой способ расчета может оказаться более трудоемким, чем предложенный выше основной способ решения, однако он является полностью формализованным и не требует творческих усилий.
Содержание
- О перспективном варианте ЕГЭ 2022 по математике. Базовый уровень.
- Задания, которых не было в прошлом году
- Задание 5.
- Задание 20.
- Как найти площадь озера на плане местности егэ
- Как найти площадь озера на плане местности егэ
О перспективном варианте ЕГЭ 2022 по математике. Базовый уровень.
С вопросами, комментариями, мнением об экзаменах обращайтесь через форму для письма, рисунок конверта кликабелен.

И, пожалуйста, напишите об ошибке, если обнаружите таковую в моих решениях.
Узнайте, как можно поддержать сайт и помочь его развитию.
Предполаганмый вариант базового ЕГЭ по мпиематике в следующем году мало отличается от вариантов прошлых лет. Основные отличия:
- Изменён порядок следования нескольких заданий. При этом содержание задания осталось прежним.
- Добавлена текстовая задача на составление уравнения или систем уравнений.
- Задача «на клеточках» изменена так, что теперь требуется не вычислить некоторое значение, а произвести его оценку.
На последнем пункте остановлюсь особо.
Обновляться интерактивная Демо-версия для экзамена 2022 будет осенью, когда утвердят контрольно-измерительные материалы ЕГЭ.
Задания, которых не было в прошлом году
Задание 5.

Задача.
На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображённого на плане. Ответ округлите до целого числа.

Поскольку шаг сетки равен 1 км, а ответ требуется дать как раз в квадратных километрах, то достаточно определить площадь озера в клеточках.
Правильным решением является следующее — ограничить исследуемый объект, в данном случае озеро, отрезками прямых линий (в других заданиях, может быть, дугами окружностей) так, чтобы приблизить его форму к простой геометрической фигуре, площадь которой легко определяется по клеткам.
В данном случае вертикальная линия в левой клетке проведена в середине квадрата, наклонные линии по диагоналям квадратов. Получаем примерно 0,5 + 1 + 0,5 + 0,5 + 0,5 = 3.
Выступающий за построенную границу участок озера и включенные внутрь береговые участки оцениваем «на глаз». Очевидно, что они приблизительно компенсируют друг друга и в совокупности создают погрешность не более полуклетки. Таким образом, округленный до целого числа ответ и есть 3.
Ответ: 3
Однако мне очень не нравится присутствие такого задания в варианте письменного экзамена, проверяемого с использованием специальных аппаратно- программных средств формально только по ответам, каковым является ЕГЭ по математике базового уровня.
Сколько раз я говорила ребятам, что этот экзамен не проверяет ваши физические возможности — остроту зрения, цветовосприятие, глазомер. Оказвается проверяет?
Сколько уговаривала ориентироваться на узлы сетки, решая задачи «на клеточках», а если какой-то элемент чертежа не попадает в узел, то использовать для вычислений геометрические формулы. Ведь задания ЕГЭ требуют однозначного ответа. Но и тогда зачастую ребята получали неточные ответы, используя методику определения длины или площади на глаз.

Полагаю, что добрая половина выпускников на реальном экзамене в этом задании смогла бы получить ответ 4. Для этого достаточно мысленно подвигать клетки с озером, получить воображаемую структуру, например, такую как на этом рисунке. Оценить площадь «нового озера» в 3,5 клетки и по правилам округления чисел в ответ записать 4.
Вывод: по моему мнению, это задача не для ЕГЭ. Она была бы очень хороша для устного экзамена, для собеседования, для практических занятий, для письменного экзамена с возможностью обоснования ответа.
Задание 20.
Следующие задания, в самом деле, нельзя назвать новыми, поскольку нынешним выпускникам они или им подобные текстовые задачи встречались на ОГЭ в 9-ом классе. Это было задание 21 во второй части варианта.
Задача.
Моторная лодка в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 30 минут, лодка отправилась назад и вернулась в пункт А в 18:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки 1 км/ч.
Для решения задач на движение важны три параметра – расстояние, время в пути и скорость движения, которые обычно обозначаются символами (S,t) и (v) соответственно. Особенность задач на движение по реке состоит в том, что движение по течению и против течения надо рассматривать отдельно.
Итак, пусть собственная скорость лодки равна (x) км/ч, тогда
- по течению: (S = 30;(км),;v = x+1;(км/ч),;t = S/v = 30/(x+1) (час));
- против течения: (S = 30;(км),;v = x-1;(км/ч),;t = S/v = 30/(x-1) (час)).
Путешествие от А до В и обратно включает движение по течению и против. Можем определить суммарное время в пути. Оно составит [frac<30>+frac<30>.] С другой стороны, лодка отсутствовала в пункте А 18−10 = 8 (часов) , из которых 2 часа 30 минут, то есть 2,5 часа находилась в пункте В. Следовательно, в пути она находилась 8−2,5 = 5,5 (часов) . Определив одну и ту же величину двумя независимыми, способами можем составмит уравнение [frac<30>+frac<30>= 5,5.] Решаем уравнение [frac<^30>+frac<^30>= ^<(x-1)(x+1)/>5,5; \ 30(x-1)+30(x+1) =5,5(x^2-1); \5,5x^2-60x -5,5 = 0; \11x^2 -120x -11 = 0, \D = 14400 + 484 = 14884, sqrt = 122,\ x_1 =frac<120 -122><22>=-frac<1><11>; ;x_2 =frac<120+122><22>= 11. ] Так как собственная скорость лодки не может быть величиной отрицательной, то для ответа подходит только второй корень уравнения 11 (км/ч).
Ответ: 11
Замечение: Об оптимизации решения квадратных уравнений см. в статье «4,5 способа решения одного квадратного уравнения».
Задача.
В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Пусть акции компании стоили А рублей и в понедельник подорожали на k%, тогда они стали стоить (100 + k)% от А, что составляет [frac<Аcdot(100+k)> <100>= Аcdotleft(1+frac<100>right) (рублей).] Полученная формула означает, что стоимость авций увеличилась в (1+k/100) раз.
Рассуждая аналогично, мы выясним, что во вторник стоимость акций по отношению к понедельнику изменилась в (1−k/100) раз, а по отношению к первоначальной стоимости в (1−4/100) раз.
Можно составить уравнение [Aleft(1+frac<100>right)left(1-frac<100>right) = Acdotleft(1-frac<4><100>right);\ 1-left(frac<100>right)^2 = 1-left(frac<2><10>right)^2\ frac <100>= frac<2><10>; ; k = 20.]
Ответ: 20.
Для решения подобных задач наиболее удобен способ вычисления процентов, описанный здесь.
Источник
Как найти площадь озера на плане местности егэ
На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображённого на плане. Ответ округлите до целого числа.
Обозначим квадраты буквами так, как показано на рисунке. Перенесём мысленно часть озера, находящуюся в квадрате D, в квадрат А. Сумма этих площадей меньше половины площади квадрата. Площадь части озера в квадрате С примерно половина площади квадрата, другая половина пустая — перенесем в неё части озера из А и D вместе взятые. Этим квадрат С будет заполнен. Теперь перенесём часть озера, лежащую ниже диагонали квадрата Е, на незанятую часть в квадрате F. Теперь квадрат F заполнен почти полностью, а квадрат Е заполнен наполовину. Итак, озеро покрывает приблизительно два полных квадрата С и F, почти полный квадрат В и половину квадрата Е. Значит, площадь озера больше 3 кв. км, но меньше 3,5 кв. км. Округляя, получаем 3 кв. км.
Примечание редакции Решу ЕГЭ.
Понимая необходимость умений проводить подобные оценки и прикидки в прикладных науках, все же отметим, что приведённые выше рассуждения не имеют никакого отношения к математике. Почему? Потому, что нет доказательств. Например, того, часть из Е действительно поместится в F. Доказательство можно было бы провести так: наложить карту на миллиметровку, найти количество квадратиков, в которые попала фигура, и точно установить границы, в которых лежит площадь: отбросив частично заполненные квадратики, получим площадь с недостатком, учитывая все частично заполненные квадратики, найдем площадь с избытком. Но это путь не для экзамена.
Примечание Д. Д. Гущина о применении палетки для определения площади.
Читательница Ольга Кулешова рассказала нам, что в начальных классах изучают способ нахождения площади фигуры с помощью палетки (квадратной сетки). Площадь фигуры считается равной количеству полностью заполненных клеток сетки плюс половина количества не полностью заполненных клеток. Решая данную задачу таким способом, найдем, что количество полностью заполненных клеток равно 0, количество частично заполненных клеток равно 6, следовательно, площадь фигуры равна 0 + 6 : 2 = 3.
Об этом необходимо сказать следующее.
Для фигур случайной формы, покрытых большим количеством клеток, указанное приближение площади нередко дает удовлетворительную точность. Однако в ряде случаев погрешность становится неприемлемой.
Найдем, к примеру, указанным методом площадь изображенных на рисунке круга и пятиугольника. Для круга сложим 5 целых клеток и половину от 16 частично заполненных, вместе 13 клеток. Как нетрудно проверить, используя формулу для площади круга найденная по клеточкам площадь круга мало отличается от расчетной. Но найдем теперь площадь пятиугольника: к 6 целым клеткам прибавим половину от 9, получим 10,5 или, округленно, 11 клеток. Однако в действительности площадь пятиугольника не 11 и даже не 10, а меньше 9 клеток. Ошибка превосходит 17%, а после округления — даже 22%.
По всей вероятности, точной формулы для оценки погрешности использования квадратной палетки при оценке площади не существует. Но ясно, что погрешность может быть достаточно велика, если все частично заполненные клетки заполнены более (либо менее), чем наполовину, или если покрывающих фигуру клеток слишком мало.
В приведенном выше задании ЕГЭ площадь покрыта всего шестью клетками. В таких случаях найденный ответ может получиться верным, но может оказаться и ошибочным. Поэтому на экзамене пользоваться указанным методом нельзя.
Подробнее прочитать о приближенном определении площадей можно, например, в учебном пособии для высших учебных заведений Инженерная геодезия.pdf.
Источник
Как найти площадь озера на плане местности егэ
На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображённого на плане. Ответ округлите до целого числа.
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
Обозначим квадраты буквами так, как показано на рисунке. Перенесём мысленно часть озера, находящуюся в квадрате D, в квадрат А. Сумма этих площадей меньше половины площади квадрата. Площадь части озера в квадрате С примерно половина площади квадрата, другая половина пустая — перенесем в неё части озера из А и D вместе взятые. Этим квадрат С будет заполнен. Теперь перенесём часть озера, лежащую ниже диагонали квадрата Е, на незанятую часть в квадрате F. Теперь квадрат F заполнен почти полностью, а квадрат Е заполнен наполовину. Итак, озеро покрывает приблизительно два полных квадрата С и F, почти полный квадрат В и половину квадрата Е. Значит, площадь озера больше 3 кв. км, но меньше 3,5 кв. км. Округляя, получаем 3 кв. км.
Примечание редакции Решу ЕГЭ.
Понимая необходимость умений проводить подобные оценки и прикидки в прикладных науках, все же отметим, что приведённые выше рассуждения не имеют никакого отношения к математике. Почему? Потому, что нет доказательств. Например, того, часть из Е действительно поместится в F. Доказательство можно было бы провести так: наложить карту на миллиметровку, найти количество квадратиков, в которые попала фигура, и точно установить границы, в которых лежит площадь: отбросив частично заполненные квадратики, получим площадь с недостатком, учитывая все частично заполненные квадратики, найдем площадь с избытком. Но это путь не для экзамена.
Примечание Д. Д. Гущина о применении палетки для определения площади.
Читательница Ольга Кулешова рассказала нам, что в начальных классах изучают способ нахождения площади фигуры с помощью палетки (квадратной сетки). Площадь фигуры считается равной количеству полностью заполненных клеток сетки плюс половина количества не полностью заполненных клеток. Решая данную задачу таким способом, найдем, что количество полностью заполненных клеток равно 0, количество частично заполненных клеток равно 6, следовательно, площадь фигуры равна 0 + 6 : 2 = 3.
Об этом необходимо сказать следующее.
Для фигур случайной формы, покрытых большим количеством клеток, указанное приближение площади нередко дает удовлетворительную точность. Однако в ряде случаев погрешность становится неприемлемой.
Найдем, к примеру, указанным методом площадь изображенных на рисунке круга и пятиугольника. Для круга сложим 5 целых клеток и половину от 16 частично заполненных, вместе 13 клеток. Как нетрудно проверить, используя формулу для площади круга найденная по клеточкам площадь круга мало отличается от расчетной. Но найдем теперь площадь пятиугольника: к 6 целым клеткам прибавим половину от 9, получим 10,5 или, округленно, 11 клеток. Однако в действительности площадь пятиугольника не 11 и даже не 10, а меньше 9 клеток. Ошибка превосходит 17%, а после округления — даже 22%.
По всей вероятности, точной формулы для оценки погрешности использования квадратной палетки при оценке площади не существует. Но ясно, что погрешность может быть достаточно велика, если все частично заполненные клетки заполнены более (либо менее), чем наполовину, или если покрывающих фигуру клеток слишком мало.
В приведенном выше задании ЕГЭ площадь покрыта всего шестью клетками. В таких случаях найденный ответ может получиться верным, но может оказаться и ошибочным. Поэтому на экзамене пользоваться указанным методом нельзя.
Подробнее прочитать о приближенном определении площадей можно, например, в учебном пособии для высших учебных заведений Инженерная геодезия.pdf.
Участок, изображенный на плане, представляет собой трапецию, площадь которой равна произведению полусуммы оснований на высоту. Таким образом, площадь участка:
Источник
На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображённого на плане. Ответ округлите до целого числа.
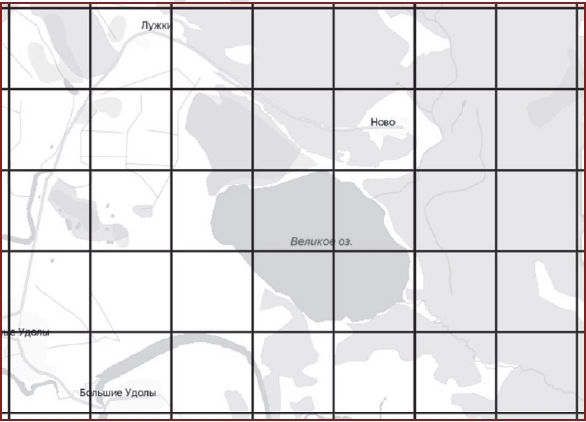
Источник: Демо (база) 2022
Решение:
1 клетка = 1 км2. Пронумеруем клетки в которых присутствует озеро от 1 до 5:
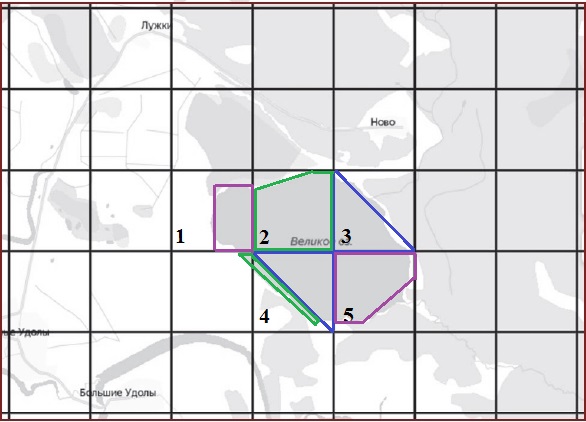
Объединим озеро в клетках 3 и 4 получим примерно 1 км2.
Объединим озеро в клетках 5 и 1 получим примерно 1 км2.
Объединим озеро в клетке 2 и остаток озера в 4й клетке получим примерно 1 км2.
Получаем площадь озера:
1 + 1 + 1 = 3 км2
Ответ: 3.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.1 / 5. Количество оценок: 29
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
как узнать площадь озера?
Ученик
(97),
закрыт
12 лет назад
Лара
Гений
(56353)
12 лет назад
Чтобы приблизительно найти, можно взять карту, на котором изображено озеро. Только на карте должен быть указан масштаб, чтобы знать, сколько в 1 см километров. Расчертить озеро на клеточки и посчитать полные клеточки и неполные. Площадь одной клеточки 1 кв. см, площадь неполных клеточек = количество клеточек / 2. Ну, и сложить, и перевести в км с учетом масштаба.
