- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какие предметы дают представление о прямоугольном параллелепипеде?
Коробка, кирпич, спичечный коробок, ящик, пакет молока или сока, платяной шкаф и т.д.
2. Из каких фигур состоит поверхность прямоугольного параллелепипеда?
Из шести прямоугольников.
3. Сколько граней имеет прямоугольный параллелепипед?
Шесть граней.
4. Сколько пар противолежащих граней имеет прямоугольный параллелепипед?
У прямоугольного параллелепипеда три паны противолежащих граней.
5. Каким свойством обладают противолежащие грани прямоугольного параллелепипеда?
Противолежащие грани прямоугольного параллелепипеда равны.
6. Как называют стороны граней прямоугольного параллелепипеда?
Стороны граней прямоугольного параллелепипеда называют рёбрами.
7. Как называют вершины граней прямоугольного параллелепипеда?
Вершины граней прямоугольного параллелепипеда называют вершинами.
8. Сколько вершин имеет прямоугольный параллелепипед?
Прямоугольный параллелепипед имеет 8 вершин.
9. Сколько рёбер имеет прямоугольный параллелепипед?
Прямоугольный параллелепипед имеет 12 рёбер.
10. Какое общее название имеют длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину?
Измерения.
11. Какие названия измерений прямоугольного параллелепипеда используют для их различия?
Длина, ширина, высота.
12. Какую фигуру называют кубом?
Куб — это прямоугольный параллелепипед, у которого все измерения равны.
13. Из каких фигур состоит поверхность куба?
Из шести равных квадратов.
14. Из каких фигур состоит поверхность пирамиды?
Поверхность пирамиды состоит из боковых граней — треугольников, имеющих общую вершину, и основания.
15. Какую пирамиду называют треугольной? Четырёхугольной?
Треугольной пирамидой называют пирамиду, у основания которой три стороны, то есть основание является треугольником.
Четырехугольной пирамидой называют пирамиду, у основания которой четыре стороны, то есть основание является четырёхугольником.
16. Что называют вершиной пирамиды?
Вершиной пирамиды называют общую вершину боковых граней.
17. Что называют рёбрами основания пирамиды?
Стороны основания пирамиды называют рёбрами основания пирамиды.
18. Что называют боковыми рёбрами пирамиды?
Боковыми рёбрами пирамиды называют стороны боковых граней, не принадлежащие основанию.
Решаем устно
1. Вычислите:
- 13 • 4 • 25 = 13 • (4 • 25) = 13 • 100 = 1 300
- 4 • 5 • 78 • 5 = (4 • 5) • 78 • 5 = (20 • 5) • 78 = 100 • 78 = 7 800
- 125 • 943 • 8 = (125 • 8) • 943 = 1 000 • 943 = 943 000
2. Упростите выражение:
- 3a • 16b = 48 ab
- 4m •9n •5k = 180 mnk
- 7a •2b •50c •8d = 5600 abcd
3. Раскройте скобки:
- 2(a + b) = 2a + 2b
- (3 — b) • 5 = 3 • 5 — b • 5 = 15 — 5b
- 6m(7n + 8p) = 6m • 7n + 6m • 8p = 42 mn + 48 mp
4. Найдите периметр прямоугольника, площадь которого равна 28 см², а одна из его сторон — 7 см.
1) 28 : 7 = 4 (см) — длина второй стороны прямоугольника.
2) (4 + 7) • 2 = 11 • 2 = 22 (см) — периметр прямоугольника.
Ответ: периметр равен 22 см.
5. В магазине разложили 6 ц яблок в ящики так, что в каждом ящике оказалось по 12 кг яблок. Сколько ящиков заполнили яблоками?
6ц = 600 кг.
600 : 12 = 50 (ящиков) — заполнили яблоками.
Ответ: 50 ящиков.
6. Во сколько раз площадь квадрата, сторона которого равна 6 см, больше площади квадрата со стороной 2 см?
1) 6 • 6 = 36 (см²) — площадь квадрата со стороной 6 см.
2) 2 • 2 = 4 (см²) — площадь квадрата со стороной 2 см.
3) 36 : 2 = 18 (раз) — площадь квадрата со стороной 6 см больше площади квадрата со стороной 2 см.
Ответ: в 18 раз.
Упражнения
598. На рисунке 169 изображён прямоугольный параллелепипед ABCDMNKP. Назовите:
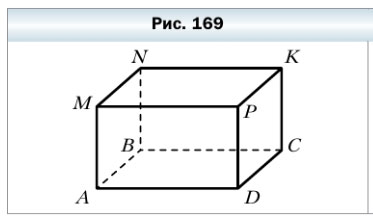
1) грани, которым принадлежит вершина С — ABCD, NKCB, PKCD
2) рёбра, равные ребру ВС — AD, MP, NK
3) верхнюю грань — MNKP
4) вершины, принадлежащие нижней грани — A, B, C, D
5) грани, имеющие общее ребро AM — AMNB, AMPD
6) грань, равную грани DPKC — AMNB
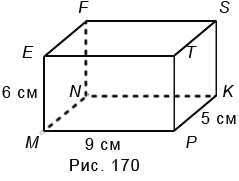
599. Измерения прямоугольного параллелепипеда MNKPEFST (рис. 170) равны 9 см, 5 см и 6 см. Вычислите сумму длин всех его рёбер и площадь его поверхности.
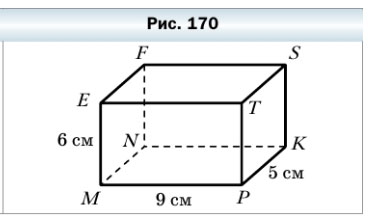
В прямоугольном параллелепипеде MNKPEFST всего 12 рёбер:
- рёбро EM = FN = SK = TP = 6 см
- рёбро MP = ET = FS = NK = 9 см
- рёбро PK = MN = EF = TS = 5 см
6 • 4 + 9 • 4 + 5 • 4 = 24 + 36 + 20 = 80 (см) — длина всех рёбер прямоугольного параллелепипеда MNKPEFST.
Поверхность прямоугольного параллелепипеда состоит из 6 граней:
- площадь грани EFST = MNKP = 5 • 9 = 45 см²
- площадь грани EFNM = TSKP = 6 • 5 = 30 см²
- площадь грани ETPM = FSKN = 9 • 6 = 54 см²
45 • 2 + 30 • 2 + 54 • 2 = 90 + 60 + 108 = 258 (см²) — площадь поверхности прямоугольного параллелепипеда MNKPEFST.
Ответ: длина всех рёбер 80 см, площадь поверхности 258 см².
600. Найдите сумму длин всех рёбер прямоугольного параллелепипеда, измерения которого равны 13 см, 16 см, 21 см.
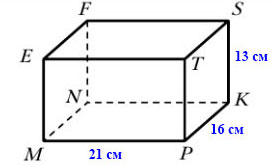
В прямоугольном параллелепипеде MNKPEFST всего 12 рёбер:
- рёбро EM = FN = SK = TP = 13 см
- рёбро MP = ET = FS = NK = 21 см
- рёбро PK = MN = EF = TS = 16 см
13 • 4 + 16 • 4 + 21 • 4 = 52 + 64 + 84 = 200 (см) — длина всех рёбер прямоугольного параллелепипеда MNKPEFST.
Ответ: длина всех рёбер 200 см.
601. Найдите площадь поверхности прямоугольного параллелепипеда, измерения которого равны 9 м, 24 м, 11 м.
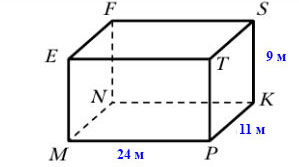
Поверхность прямоугольного параллелепипеда состоит из 6 граней:
- площадь грани EFST = MNKP = 24 • 11 = 264 м²
- площадь грани EFNM = TSKP = 9 • 11 = 99 м²
- площадь грани ETPM = FSKN = 24 • 9 = 216 м²
264 • 2 + 99 • 2 + 216 • 2 = 528 + 198 + 432 = 1 158 (м²) — площадь поверхности прямоугольного параллелепипеда MNKPEFST.

Ответ: площадь поверхности 1 158 м².
602. Вычислите площадь поверхности и сумму длин всех рёбер куба (рис. 171), ребро которого равно 5 см.
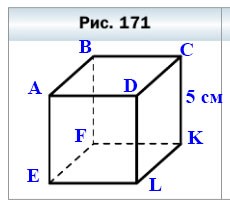
В кубе ABCDEFKL всего 12 рёбер и они все равны 5 см.
5 • 12 = 60 (см) — длина всех рёбер куба ABCDEFKL.
Поверхность куба состоит из 6 граней и они все равны 5 • 5 = 25 см²
25 • 6 = 150 (см²) — площадь поверхности куба ABCDEFKL.
Ответ: длина всех рёбер 60 см, площадь поверхности 150 см².
603. Найдите сумму длин всех рёбер и площадь поверхности куба, если его ребро равно 7 см.

В кубе ABCDEFKL всего 12 рёбер и они все равны 7 см.
7 • 12 = 84 (см) — длина всех рёбер куба ABCDEFKL.
Поверхность куба состоит из 6 граней и они все равны 7 • 7 = 49 см²
49 • 6 = 294 (см²) — площадь поверхности куба ABCDEFKL.
Ответ: длина всех рёбер 84 см, площадь поверхности 294 см².
604. На рисунке 172 изображена пирамида МАВС. Укажите:
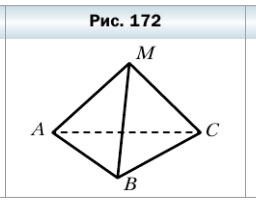
1) основание пирамиды — ABC
2) вершину пирамиды — M
3) боковые грани пирамиды — AMB, AMC, BMC
4) боковые рёбра пирамиды — AM, BM, CM
5) рёбра основания пирамиды — AB, BC, AC
605. На рисунке 173 изображена пирамида SABCD. Укажите:

1) основание пирамиды — ABCD
2) вершину пирамиды — S
3) боковые грани пирамиды — ADS, DCS, CBS, ABS
4) боковые рёбра пирамиды — AS, BS, CS, DS
5) рёбра основания пирамиды — AB, BC, CD, DA
606. На рисунке 174 изображена развёртка прямоугольного параллелепипеда.
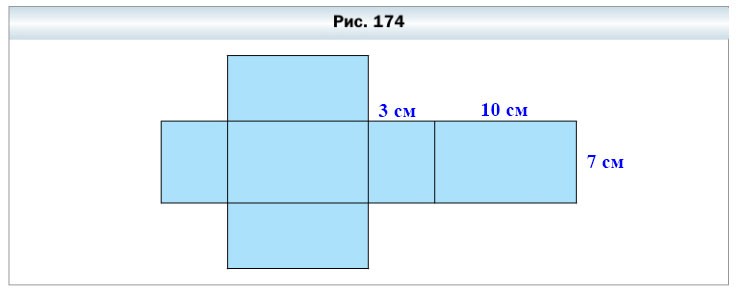
1) Из скольких прямоугольников состоит развёртка? — из 6 прямоугольников.
2) Сколько пар равных прямоугольников содержит развёртка? — 3-х пары равных прямоугольников.
3) Какова площадь этой развёртки, если измерения параллелепипеда равны 10 см, 7 см и 3 см?
S = (10 • 7) • 2 + (3 • 10) • 2 + (7 • 3) • 2 = 70 • 2 + 30 • 2 + 21 • 2 = 140 + 60 + 42 = 242 см²
607. Вычислите площадь поверхности прямоугольного параллелепипеда, развёртка которого изображена на рисунке 175.
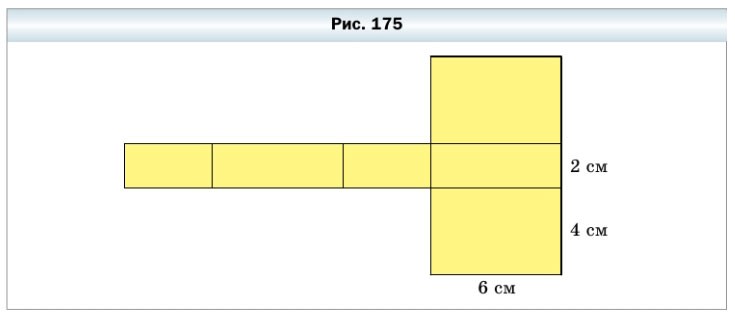
S = (6 • 4) • 2 + (6 • 2) • 2 + (4 • 2) • 2 = 24 • 2 + 12 • 2 + 8 • 2 = 48 + 24 + 16 = 88 см²
Ответ: площадь поверхности равна 88 см².
608. Высота прямоугольного параллелепипеда равна 20 см, что на 5 см больше его ширины и в 3 раза меньше его длины. Вычислите площадь поверхности параллелепипеда.

1) 20 — 5 = 15 (см) — ширина прямоугольного параллелепипеда.
2) 20 • 3 = 60 (см) — длина прямоугольного параллелепипеда
3) (60 • 20) • 2 + (60 • 15) • 2 + (20 • 15) • 2 = 1 200 • 2 + 900 • 2 + 300 • 2 = 2 400 + 1 800 + 600 = 4 800 (см²) — площадь поверхности прямоугольного параллелепипеда.
Ответ: S = 4 800 см².
609. Сумма длин всех рёбер прямоугольного параллелепипеда равна 28 см. Найдите сумму длин трёх его рёбер, имеющих общую вершину.
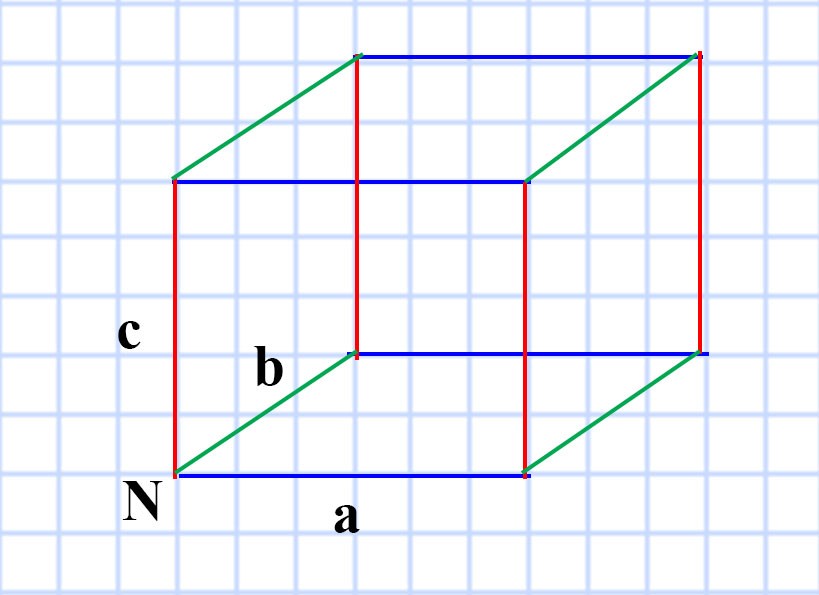
В прямоугольном параллелепипеде всего 12 ребер. Причём:
- 4 ребра равны длине a — рёбра синего цвета
- 4 ребра равны ширине b — рёбра зелёного цвета
- 4 ребра равны ширине c — рёбра красного цвета
Мы знаем, что сумма длин всех рёбер этого прямоугольного параллелепипеда равна 28 см.
Значит, можно записать:
4a + 4b + 4с = 28
4 (a + b + с ) = 28
a + b + с = 28 : 4
a + b + с = 7 (см)
Так как рёбра a, b и с сходятся в общей вершине N, то искомая сумма длин трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину равна 7 см.
Ответ: 7 см.
610. Прямоугольный параллелепипед и куб имеют равные площади поверхностей. Длина параллелепипеда равна 18 м, что в 2 раза больше, чем его ширина, и на 8 м больше, чем его высота. Найдите ребро куба.

1) 18 : 2 = 9 (м) — ширина параллелепипед.
2) 18 — 8 = 10 (м) — высота параллелепипеда.
3) (18 • 9) • 2 + (18 • 10) • 2 + (10 • 9) • 2 = 162 • 2 + 180 • 2 + 90 • 2 = 324 + 360 + 180 = 864 (м²) — площадь поверхности параллелограмма.
Значит площадь поверхности куба равна 864 м². Так как у куба всего 6 граней и все они одинаковы, то можно найти площадь грани куба.
4) 864 : 6 = 144 (м²) — площадь грани куба.
Для того, чтобы найти длину ребра куба, надо подобрать такое число, квадрат которого будет равняться числу 144. Это число 12 (12 • 12 = 144).
Значит длина ребра куба равна 12 м.
Ответ: 12 метров.
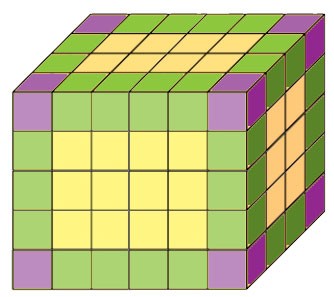
611. Брусок, имеющий форму прямоугольного параллелепипеда с измерениями 4 см, 5 см и 6 см, покрасили со всех сторон и разрезали на кубики с ребром 1 см. Сколько получилось кубиков, у которых:
1) окрашено три грани — 8 кубиков (фиолетовые), которые расположены по вершинам прямоугольного параллелепипеда.
2) окрашено две грани — 36 кубков (зелёные), которые расположены по рёбрам параллелепипеда, но не являются его вершинами (4 • 4 + 3 • 4 + 2 • 4 = 16 + 12 + 8 = 36):
- по 4 кубика на 4 рёбрах длиной 6 см
- по 3 кубика на 4 рёбрах длиной 5 см
- по 2 кубика на 4 рёбрах длиной 4 см
3) окрашено одна грань — 52 кубика (жёлтые), которые не примыкают ни к вершинам, ни к рёбрам параллелепипеда (12 • 2 + 8 • 2 + 6 • 2 = 24 + 16 + 12 = 52):
- 4 • 3 = 12 кубиков на двух гранях размерами 6 см х 5 см
- 4 • 2 = 8 кубиков на двух гранях размерами 6 см х 4 см
- 3 • 2 = 6 кубиков на двух гранях размерами 5 см х 5 см
Упражнения для повторениях
612. Скорость космического корабля «Восток», на котором Юрий Гагарин совершил свой полёт, равна 8 км/с.
1) За сколько минут он пролетал 960 км?
960 : 8 = 120 (с) — нужно кораблю для преодоления 960 км.
120 с = 2 мин
Ответ: 2 минуты.
2) Какое расстояние он пролетал за 1 ч?
1 ч = 60 мин = 3 600 с
8 • 3 600 = 28 800 (км) — пролетает корабль за 1 час.
Ответ: 28 800 км.
613. Из листа картона можно вырезать шесть одинаковых квадратов. Сколько листов картона надо для того, чтобы вырезать 50 таких квадратов?
50 = 6 • 8 + 2
Значит нужно 8 + 1 = 9 листов.
Ответ: 9 листов.
614. Поезд отправился со станции в 16 ч со скоростью 54 км/ч. В 19 ч с этой же станции в противоположном направлении отправился второй поезд. В 24 ч расстояние между ними было равно 642 км. С какой скоростью двигался второй поезд?

1) 24 — 16 = 8 (часов) — двигался первый поезд.
2) 54 • 8 = 432 (км) — проехал первый поезд за 8 часов.
3) 24 — 19 = 5 (часов) — двигался второй поезд.
4) 642 — 432 = 210 (км) — проехал второй поезд за 5 часов.
5) 210 : 5 = 42 (км/ч) — скорость второго поезда.
Ответ: 42 км/ч.
615. Решите уравнение:

Задача от мудрой совы
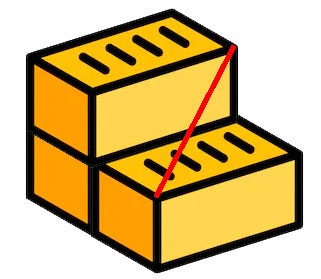
616. Как с помощью линейки измерить диагональ кирпича, имея ещё несколько таких кирпичей? (Диагональ параллелепипеда — это отрезок, соединяющий две его вершины, не принадлежащие одной грани.)
Для этого нам потребуется как минимум 3 кирпича:
- Сложим кирпичи лесенкой
- Линейкой измерим расстояние так, как показано на рисунке.
- Измеренное расстояние будет точно соответствовать длине диагонали кирпича.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
-
Главная
-
ГДЗ
- 5 класс
- Математика
-
Мерзляк учебник
- 599
Вернуться к содержанию учебника
Страница 151
594
595
596
597
598
599
600
601
602
603
604
Вопрос
Измерения прямоугольного параллелепипеда MNKPEFST (рис. 170) равны 9 см, 5 см и 6 см. Вычислите сумму длин всех его рёбер и площадь его поверхности.
Подсказка
Вспомните:
- Что такое прямоугольный параллелепипед и какие у него элементы.
- Что называют измерениями прямоугольного параллелепипеда.
- Как найти площадь поверхности прямоугольного параллелепипеда.
Ответ
594
595
596
597
598
599
600
601
602
603
604



594
595
596
597
598
599
600
601
602
603
604
Вернуться к содержанию учебника
Запишите формулу для вычисления площади S поверхности:
1) куба, ребро которого равно a:
S = _;
2) прямоугольного параллелепипеда, измерения которого равна a, b и c:
S = _

reshalka.com
ГДЗ рабочая тетрадь №1 по математике 5 класс Мерзляк. §22. Прямоугольный параллелепипед. Пирамида. Номер №272
Решение 1
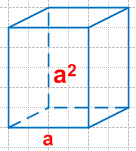
Площадь одной грани куба равна
a
2
.
Куб имеет 6 одинаковых граней, тогда площадь поверхности куба будет иметь формулу:
S
=
6
a
2
Решение 2
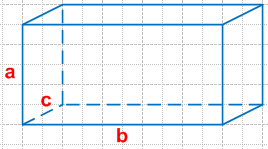
Прямоугольный параллелепипед имеет 3 пары противоположных равных граней, которые имеют площади: ac, bc, ab.
Тогда площадь поверхности прямоугольного параллелепипеда будет иметь формулу:
S = 2 * (ac + bc + ab)
ГДЗ и решебники
вип уровня
- ГДЗ
- 5 класс
- Математика
- Мерзляк
- Упражнение 601

Условие
Найдите площадь поверхности прямоугольного параллелепипеда, измерения которого равны 9 м, 24 м, 11 м.
Решение 1

Решение 2

Решение 3

Решение 4
Популярные решебники
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)

Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.

