Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачу из 23 задания ОГЭ по математике.
Задача
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC = 11, а расстояние от точки K до стороны AB равно 3.
Построим рисунок и напишем условие
Решение:
1) Запишем формулу нахождения площади параллелограмма для нашей фигуры. Для этого проведем высоту EH через точку пересечения биссектрис.
По условию нам известна сторона BC=11. По свойству параллелограмма, противоположные стороны равны, значит AD=BC=11
2) Для нахождения площади параллелограмма, необходимо найти высоту EH. Для этого рассмотрим пары треугольников AKH и AFK, FBK и EBK
3) Докажем, что треугольники AFK и AKH равны.
4) Аналогично докажем, что треугольники FBK и EBK равны
По выше доказанному, мы получили, что
5) Найдем высоту параллелограмма EH
6) Найдем площадь параллелограмма по формуле из пункта 1
Ответ 66
Вам понравился материал? Поблагодарить легко! Будем весьма признательны, если поделитесь этой статьей в социальных сетях, поставите лайк и подпишитесь на мой блог
1. Формула площади параллелограмма через стороны и углы

a, b – стороны параллелограмма
α, β – углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):

Калькулятор – вычислить, найти площадь параллелограмма:
a(сторона)=
b(сторона)=
α или β (угол в градусах)= ( sin α=sin β )
S=
2. Формула площади параллелограмма через сторону и высоту

a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D – большая диагональ
d –меньшая диагональ
α, β – углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):

Калькулятор – вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
Задача
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K.
Найти площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 10.
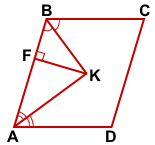 Дано: ABCD — параллелограмм,
Дано: ABCD — параллелограмм,
AK, BK — биссектрисы углов BAD и ABC,
AK∩BK=K, KF⊥AB,
KF=10, BC=19
Найти: SABCD
Решение:
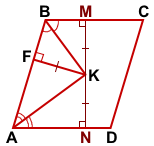 Проведём через точку K высоту параллелограмма MN.
Проведём через точку K высоту параллелограмма MN.
Так как любая точка биссектрисы угла равноудалена от его сторон, то
KM=KF=10, KN=KF=10.
MN=KM+KN=20.
По формуле S=a∙h
площадь параллелограмма SABCD=BC∙MN, SABCD=19∙10=190.
Ответ: 190.
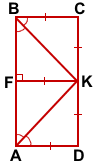
Замечание
В частном случае, если BC=KF, ABCD — прямоугольник, и K — середина CD.
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Значит отрезок, который BK отсекает на стороне CD, равен BC.
Расстояние от K до BC равно длине перпендикуляра, опущенного из точки K на прямую BC.
Из данной точки к данной прямой можно провести только один перпендикуляр. Значит CK⊥BC. Следовательно, ABCD — прямоугольник.
Параллелограмм и его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма
Параллелограмм —
это четырехугольник, имеющий две пары
параллельных сторон.
Свойства
параллелограмма:
-
Противоположные стороны параллелограмма
равны. -
Противоположные
углы параллелограмма равны. -
Диагонали
параллелограмма в точке пересечения
делятся пополам.
Давайте
посмотрим, как свойства параллелограмма
применяются в решении задач ЕГЭ.
1.
Найдите угол между биссектрисами углов
параллелограмма, прилежащих к одной
стороне. Ответ дайте в градусах.
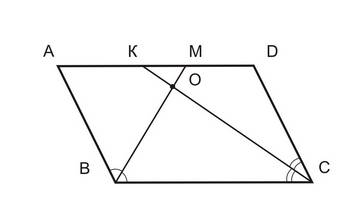
Пусть
ВМ и СК — биссектрисы углов
параллелограмма, прилежащих к стороне
ВС. Сумма углов АВС и BCD равна 180°. Углы
ОВС и ОСВ — половинки углов АВС
и ВСD. Значит, сумма углов АВС и ВСD
равна 90 градусов. Из треугольника
ВОС находим, что угол ВОС — прямой.
Ответ: 90.
Биссектрисы
углов параллелограмма, прилежащих
к одной стороне, — перпендикулярны.
Легко
доказывается и другое свойство
биссектрис параллелограмма:
Биссектрисы
противоположных углов параллелограмма —
параллельны.
2.
Точка пересечения биссектрис двух углов
параллелограмма, прилежащих к одной
стороне, принадлежит противоположной
стороне. Меньшая сторона параллелограмма
равна 5. Найдите его большую сторону.
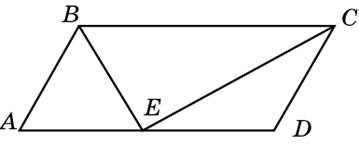
Найдем
на этом рисунке накрест лежащие углы.
Мы уже рассказывали, что это такое.
Углы
СВЕ и ВЕА, а также СЕD и ВСЕ —
накрест лежащие. Накрест лежащие углы
равны. Значит, угол СВЕ равен углу ВЕА,
а угол СЕD — углу ВСЕ.
Получаем,
что треугольники АВС и CDE —
равнобедренные, то есть АЕ = АВ, а DЕ
= CD. Тогда AD = 5 + 5 = 10.
Биссектриса
угла параллелограмма отсекает от него
равнобедренный треугольник.
Запишем
формулы
площади параллелограмма:
S
= ah, где а — основание параллелограмма,
h — его высота.
S = ab sin φ, где
а и b — стороны параллелограмма,
φ — угол между ними.
И еще
одна формула. Так же, как и свойства
биссектрис углов параллелограмма, эта
формула пригодится тем, кто нацелен
на решение задачи С4.
S
=
![]()
d1 d2 sin α,
где d1 и d2 — диагонали
параллелограмма, α — угол между ними.
Прямоугольник
и его свойства
Прямоугольник —
это параллелограмм, у которого все
углы прямые.
Диагонали
прямоугольника равны.
1.
В прямоугольнике диагональ делит
угол в отношении 1:2, меньшая его
сторона равна 6. Найдите диагональ
данного прямоугольника.
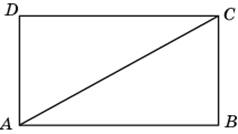
Всё
просто. Рассмотрите прямоугольный
треугольник АВС. Найдите, чему равен
угол САВ и его синус, а затем найдите
АС.
Ответ:
12.
А сейчас
рассмотрим еще одну задачу, в которой
применяются свойства диагоналей
прямоугольника.
2.
Острые углы прямоугольного треугольника
равны 24° и 66°. Найдите угол между
высотой и медианой, проведенными
из вершины прямого угла. Ответ дайте
в градусах.
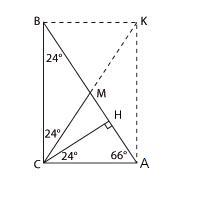
Казалось бы,
при чем здесь прямоугольник? Дан
прямоугольный треугольник, из вершины
прямого угла проведены высота и медиана.
А что можно сказать о длине этой
медианы?
Давайте
достроим чертеж до прямоугольника.
Поскольку диагонали прямоугольника
равны (это свойство прямоугольника)
и делятся пополам в точке пересечения,
отрезки СМ, ВМ и АМ тоже будут
равны. Каждый из них равен половине
диагонали прямоугольника. Мы доказали
теорему:
В прямоугольном
треугольнике медиана, проведенная
к гипотенузе, равна половине гипотенузы.
Итак,
ВМ = СМ, значит, треугольник ВМС
равнобедренный, и угол ВСМ равен 24°.
По свойству
высоты, проведенной из вершины прямого
угла,
∠АСН
= ∠АВС
= 24°.
Тогда
угол МСН (между медианой и высотой
треугольника АВС) равен 90° – 24° –
24° = 42°.
Ответ: 42.
Как
вы думаете, где находится центр
окружности, описанной вокруг прямоугольного
треугольника? Ведь центр описанной
окружности — точка, равноудаленная
от всех вершин треугольника. Очевидно,
эта точка — середина гипотенузы.
В прямоугольном
треугольнике центром описанной окружности
является середина гипотенузы.
1.
Найдите диагональ прямоугольника,
вписанного в окружность, радиус
которой равен 5.
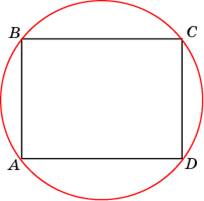
Проведем
диагональ АС. Получим, что АС равна
2R.
Ответ: 10.
Ромб
и его свойства
По определению,
ромб — это параллелограмм, все стороны
которого равны.
Свойства
ромба:
-
Диагонали
ромба перпендикулярны. -
Диагонали
ромба делят его углы пополам.
Воспользуемся
свойствами ромба для решения задач.
1.
Найдите меньшую диагональ ромба, стороны
которого равны 2, а острый угол
равен 60°.
Проведите
меньшую диагональ ромба и рассмотрите
треугольник ADB. Поскольку AD = DB, а угол
DAB равен 60°, треугольник ADB —
равносторонний. Следовательно, меньшая
диагональ ромба равна 2.
1.
Найдите высоту ромба, сторона которого
равна v3, а острый угол равен 60?.
Один
из подходов к решению задач
по геометрии — метод площадей.
Он состоит в том, что площадь фигуры
выражается двумя разными способами,
а затем из полученного уравнения
находится неизвестная величина.
Пусть
а — сторона ромба. Тогда
S
= a2
sin 60° = ah,
![]()
Отсюда
![]()
.
2.
Диагонали ромба относятся как 3:4. Периметр
ромба равен 200. Найдите высоту ромба.
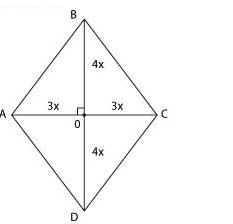
Пусть
диагонали ромба равны 6х и 8х.
Диагонали ромба перпендикулярны,
значит, треугольник АОВ — прямоугольный.
По теореме Пифагора АВ2
= АО2
+ ОВ2
АВ2
= 9×2
+ 16×2,
АВ2
= 25×2,
Отсюда АВ = 5х.
Поскольку периметр
равен 200,
5х · 4 = 200
х = 10, АВ = 50,
а диагонали ромба равны 60 и 80.
Нам
надо найти высоту ромба.
Давайте
запишем, чему равна площадь ромба.
С одной стороны, S = ah. С другой
стороны, площадь ромба складывается
из площадей двух равных треугольников
АВС и ADC, то есть равна 60 · 40 = 2400.
Отсюда h = S : a = 2400 : 50 = 48.
Ответ:
48.
Квадрат —
определение и свойства
Квадрат —
это прямоугольник, у которого все
стороны равны.
Можно дать и другое определение
квадрата:
квадрат —
это ромб, у которого все углы прямые.
Получается,
что квадрат обладает всеми свойствами
параллелограмма, прямоугольника и ромба.
Перечислим
свойства
квадрата:
-
Все
углы квадрата — прямые, все стороны
квадрата — равны. -
Диагонали
квадрата равны и пересекаются под
прямым углом. -
Диагонали
квадрата делят его углы пополам.
Площадь
квадрата, очевидно, равна квадрату его
стороны: S = a2.
Диагональ квадрата равна произведению
его стороны на
,
то есть
![]()
,
Разберем
несколько простых задач на тему
«Квадрат». Все они взяты из Банка
заданий ФИПИ.
1.
Найдите сторону квадрата, диагональ
которого равна
![]()
.
Мы знаем,
что
.
Тогда
![]()
.
2.
Найдите радиус окружности, описанной
около квадрата со стороной, равной
![]()
.

Очевидно,
радиус окружности равен диагонали
квадрата.
Ответ:
4.
3.
Найдите сторону квадрата, описанного
около окружности радиуса 4.

Диаметр
окружности равен стороне квадрата.
Ответ:
8.
4.
Найдите радиус окружности, вписанной
в квадрат ABCD, считая стороны квадратных
клеток равными
![]()
.
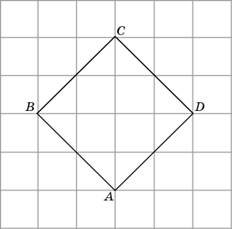
Чуть
более сложная задача. Нарисуйте
окружность, вписанную в данный
квадрат, то есть касающуюся всех его
сторон. Вы увидите, что диаметр этой
окружности равен стороне квадрата.
Ответ:
2.
5.
Найдите радиус r окружности, вписанной
в четырехугольник ABCD. В ответе
укажите
![]()
.
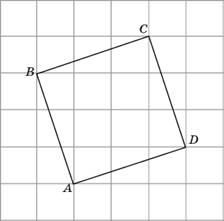
Считаем
стороны клеток равными единице.
Четырехугольник ABCD — квадрат. Все
его стороны равны, все углы — прямые.
Как и в предыдущей задаче, радиус
окружности, вписанной в квадрат,
равен половине его стороны.
Найдем
на чертеже прямоугольный треугольник.
По теореме Пифагора найдем сторону,
например, АВ. Она равна
![]()
.
Тогда радиус вписанной окружности равен
![]()
.
В ответ запишем
![]()
.
Ответ:
5.
Трапеция
и ее свойства
Трапеция —
четырехугольник, у которого две
стороны параллельны, а две другие —
нет.
Параллельные
стороны трапеции называются основаниями.
Другие две — боковые стороны.
Если
боковые стороны равны, трапеция называется
равнобедренной.
Площадь
трапеции равна произведению полусуммы
оснований на высоту:
![]()
Отрезок,
соединяющий середины оснований трапеции,
называется средней линией трапеции.
Средняя линия трапеции параллельна
основаниям, а длина ее равна
полусумме оснований:
![]()
Как
видим, теория очень проста. А задачи,
в которых применяются свойства
трапеции, весьма разнообразны. В этой
статье разобраны и стандартные задачи
(номер 1 и 2), и более интересные.
1.
Найдите высоту трапеции ABCD, опущенную
из вершины B, если стороны квадратных
клеток равны
.
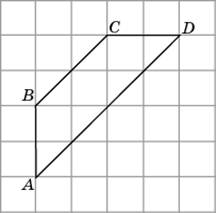
Высота
трапеции — это отрезок, перпендикулярный
ее основаниям. Проведем высоту
из вершины В.
Ответ:
2.
2.
Основания трапеции равны 18 и 6,
боковая сторона, равная 7, образует
с одним из оснований трапеции угол
150. Найдите площадь трапеции.
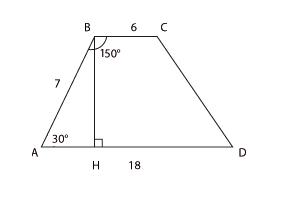
Это
стандартная задача. Углы АВН и ВАН —
односторонние, значит, их сумма равна
180°, и тогда угол ВАН равен 30°.
Из треугольника АВН найдем высоту
ВН. Катет, лежащий напротив угла в 30,
равен половине гипотенузы. Получаем,
что ВН = 3,5 и площадь трапеции
равна 42.
3.
Основания трапеции равны 4 и 10.
Найдите больший из отрезков, на которые
делит среднюю линию этой трапеции одна
из ее диагоналей.
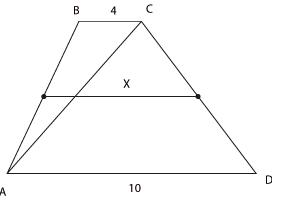
Скажите,
что вы видите на чертеже? Можно
сказать, что изображена трапеция АВСD,
и в ней проведена средняя линия.
А можно увидеть и другое — два
треугольника, АВС и АСD, в которых
проведены средние линии.
Мы помним,
что средняя линия треугольника —
это отрезок, соединяющий середины двух
его сторон. Средняя линия треугольника
параллельна третьей его стороне и равна
половине этой стороны.
Из треугольника
АВD находим: х = 5.
В следующей
задаче мы тоже воспользуемся свойством
средней линии треугольника.
4.
Основания трапеции равны 3 и 2.
Найдите отрезок, соединяющий середины
диагоналей трапеции.
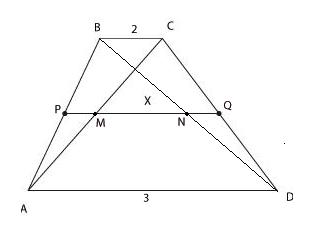
Проведем
PQ — среднюю линию трапеции, PQ = 2,5.
Легко доказать, что отрезок MN,
соединяющий середины диагоналей
трапеции, лежит на средней линии.
Дальше все просто. Найдем отрезки РМ
и NQ, являющиеся средними линиями
треугольников ABC и BCD, а затем
отрезок MN. Он равен 0,5.
5.
Прямая, проведенная параллельно боковой
стороне трапеции через конец меньшего
основания, равного 4, отсекает
треугольник, периметр которого равен
15. Найдите периметр трапеции.
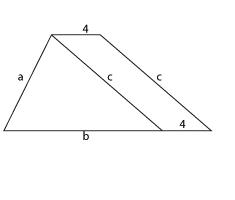
Периметр
треугольника равен сумме его сторон,
то есть a + b + c.
Периметр трапеции
равен а + b + 4 + c + 4.
На сколько
периметр трапеции больше периметра
треугольника? Чему равен периметр
трапеции?
Ответ:
23.
Окружность.
Центральный и вписанный угол
Центральный
угол —
это угол, вершина которого находится
в центре окружности.
Вписанный
угол —
угол, вершина которого лежит на окружности,
а стороны пересекают ее.
На рисунке —
центральные и вписанные углы, а также
их важнейшие свойства.
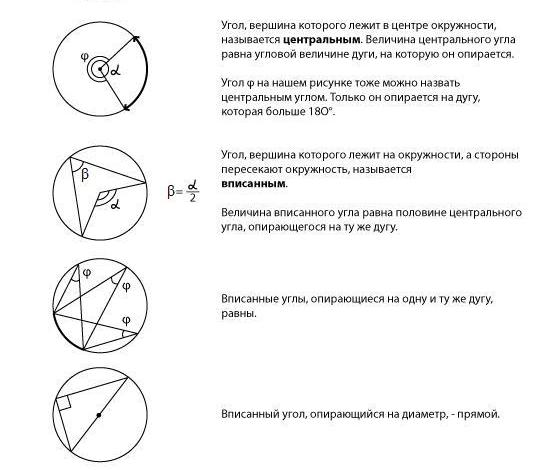
Итак,
величина
центрального угла равна угловой величине
дуги, на которую он опирается.
Значит,
центральный угол величиной в 90 градусов
будет опираться на дугу, равную 90°,
то есть
![]()
круга.
Центральный угол, равный 60°, опирается
на дугу в 60 градусов, то есть
на шестую часть круга.
Величина
вписанного угла в два раза меньше
центрального, опирающегося на ту же
дугу.
Также
для решения задач нам понадобится
понятие «хорда».

Равные
центральные углы опираются на равные
хорды.
1.
Чему равен вписанный угол, опирающийся
на диаметр окружности? Ответ дайте
в градусах.
Вписанный
угол, опирающийся на диаметр, —
прямой.
Ответ:
90.
2.
Центральный угол на 36° больше
острого вписанного угла, опирающегося
на ту же дугу окружности. Найдите
вписанный угол. Ответ дайте в градусах.
Пусть
центральный угол равен х, а вписанный
угол, опирающийся на ту же дугу,
равен у.
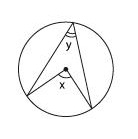
Мы знаем,
что х = 2у.
Отсюда 2у = 36 + у,
у = 36.
Ответ:
36.
3.
Радиус окружности равен 1. Найдите
величину тупого вписанного угла,
опирающегося на хорду, равную
.
Ответ дайте в градусах.
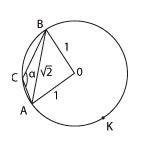
Пусть
хорда АВ равна
.
Тупой вписанный угол, опирающийся на эту
хорду, обозначим ?.
В треугольнике
АОВ стороны АО и ОВ равны 1,
сторона АВ равна
.
Нам уже встречались такие треугольники.
Очевидно, что треугольник АОВ —
прямоугольный и равнобедренный,
то есть угол АОВ равен 90°.
Тогда
дуга АСВ равна 90°, а дуга АКВ равна
360° — 90° = 270°.
Вписанный угол
? опирается на дугу АКВ и равен
половине угловой величины этой дуги,
то есть 135°.
Ответ:
135.
4.
Хорда AB делит окружность на две
части, градусные величины которых
относятся как 5:7. Под каким углом видна
эта хорда из точки C, принадлежащей
меньшей дуге окружности? Ответ дайте
в градусах.
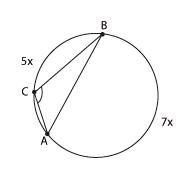
Главное
в этой задаче — правильный чертеж
и понимание условия. Как вы понимаете
вопрос: «Под каким углом хорда видна
из точки С?»
Представьте, что
вы сидите в точке С и вам
необходимо видеть всё, что происходит
на хорде АВ. Так, как будто хорда АВ —
это экран в кинотеатре 🙂
Очевидно,
что найти нужно угол АСВ.
Сумма двух
дуг, на которые хорда АВ делит
окружность, равна 360°, то есть
5х +
7х = 360°
Отсюда х = 30°, и тогда вписанный
угол АСВ опирается на дугу, равную
210°.
Величина вписанного угла равна
половине угловой величины дуги, на которую
он опирается, значит, угол АСВ равен
105°.
Ответ:
105.
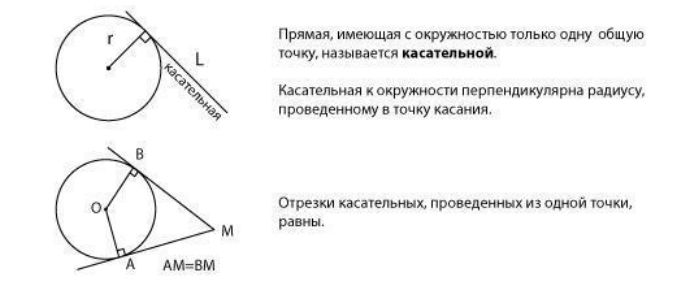
Касательная
к окружности
Касательная
к окружности — прямая, имеющая
с окружностью единственную общую
точку.
Понятие
касательной к окружности и основные
свойства касательной проиллюстрированы
ниже на рисунке.
1.
Угол ACO равен 28°, где O — центр
окружности. Его сторона CA касается
окружности. Найдите величину меньшей
дуги AB окружности, заключенной внутри
этого угла. Ответ дайте в градусах.
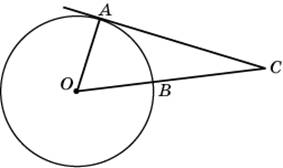
Касательная
к окружности перпендикулярна радиусу,
проведенному в точку касания. Значит,
угол САО — прямой. Из треугольника
АСО получим, что угол АОС равен 62 градуса.
Величина центрального угла равна угловой
величине дуги, на которую он опирается,
значит, величина дуги АВ — тоже
62 градуса.
Ответ:
62.
2.
Найдите угол ACO, если его сторона CA
касается окружности, O — центр
окружности, а большая дуга AD
окружности, заключенная внутри этого
угла, равна 116°. Ответ дайте в градусах.
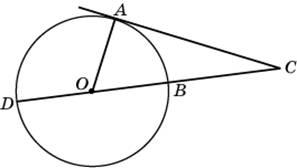
Это
чуть более сложная задача. Центральный
угол АОD опирается на дугу AD,
следовательно, он равен 116 градусов.
Тогда угол АОС равен 180° – 116° = 64°.
Касательная перпендикулярна радиусу,
проведенному в точку касания, значит,
угол ОАС — прямой. Тогда угол АСО
равен 90° – 64° = 26°.
Ответ:
26.
3.
Хорда AB стягивает дугу окружности
в 92°. Найдите угол ABC между этой хордой
и касательной к окружности,
проведенной через точку B. Ответ дайте
в градусах.
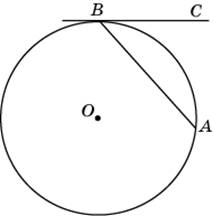
Проведем
радиус ОВ в точку касания, а также
радиус ОА. Угол ОВС равен 90°. Треугольник
ВОА — равнобедренный. Нетрудно найти,
что угол ОВА равен 44 градуса, и тогда
угол СВА равен 46 градусов, то есть
половине
угловой величины дуги АВ.
Получается,
что
угол между касательной и хордой,
проведенной через точку касания, равен
половине угловой величины дуги,
заключенной между ними.
4.
Через концы A, B дуги окружности
в 62° проведены касательные AC
и BC. Найдите угол ACB. Ответ дайте
в градусах.
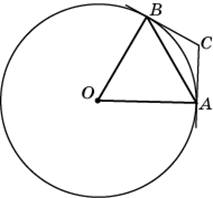
Рассмотрите
четырехугольник ОВСА. Сумма углов любого
выпуклого четырехугольника равна 360°.
Углы ОВА и ОВС и ОАС — прямые,
угол ВОА равен 62°, значит, угол АСВ
равен 28 градусов.
Ответ:
28.
5.
К окружности, вписанной в треугольник
ABC, проведены три касательные. Периметры
отсеченных треугольников равны 6, 8, 10.
Найдите периметр данного треугольника.
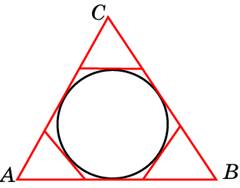
Вспомним
еще одно важное свойство касательных
к окружности:
Отрезки
касательных, проведенных из одной
точки, равны.
Периметр треугольника — это сумма
всех его сторон. Обратите внимание
на точки на нашем чертеже, являющиеся
вершинами шестиугольника. Из каждой
такой точки проведены два отрезка
касательных к окружности. Отметьте
на чертеже такие равные отрезки. Еще
лучше, если одинаковые отрезки вы будете
отмечать одним цветом. Постарайтесь
увидеть, как периметр треугольника АВС
складывается из периметров отсеченных
треугольников.
Ответ:
24.
Все
эти задачи встречаются в Банке заданий
ФИПИ под номером В6. А вот одна
из сложных задач В3:
6.
Около окружности описан многоугольник,
площадь которого равна 5. Его периметр
равен 10. Найдите радиус этой окружности.
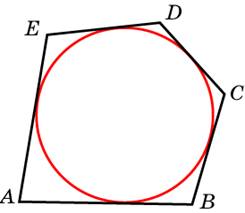
Обратите
внимание — в условии даже не сказано,
сколько сторон у этого многоугольника.
Видимо, это неважно. Пусть их будет
пять, как на рисунке.
Окружность
касается всех сторон многоугольника.
Отметьте центр окружности — точку
О — и проведите перпендикулярные
сторонам радиусы в точки касания.
Соедините
точку О с вершинами А, В, С, D, E.
Получились треугольники АОВ, ВОС, СОD,
DOE и ЕОА.
Очевидно, что площадь
многоугольника S = SАОВ
+ SВОС
+ SСОD
+ SDOE
+ SЕОА.
Как вы думаете, чему равны высоты
всех этих треугольников и как,
пользуясь этим, найти радиус окружности?
Ответ:
1.
На этой странице вы узнаете
- Чем отличаются признаки от свойств?
- Сколько крыс у биссектрисы?
- Гибридом чего будет квадрат?
Когда мы видим изображение с множеством деталей, наш мозг автоматически раскладывает их на простые фигуры. Этот процесс занимает доли секунды. Разные геометрические фигуры вызывают у нас разные ощущения, эмоции и ассоциации.А что будет, если мы задержим взгляд на одной из них и разберем подробнее? Давайте сделаем так с параллелограммом.
Параллелограмм
Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.

Параллелограмм мы видим достаточно часто.


Признаки параллелограмма
У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.
Признаки параллелограмма:
- Две противоположные стороны четырехугольника параллельны и равны.
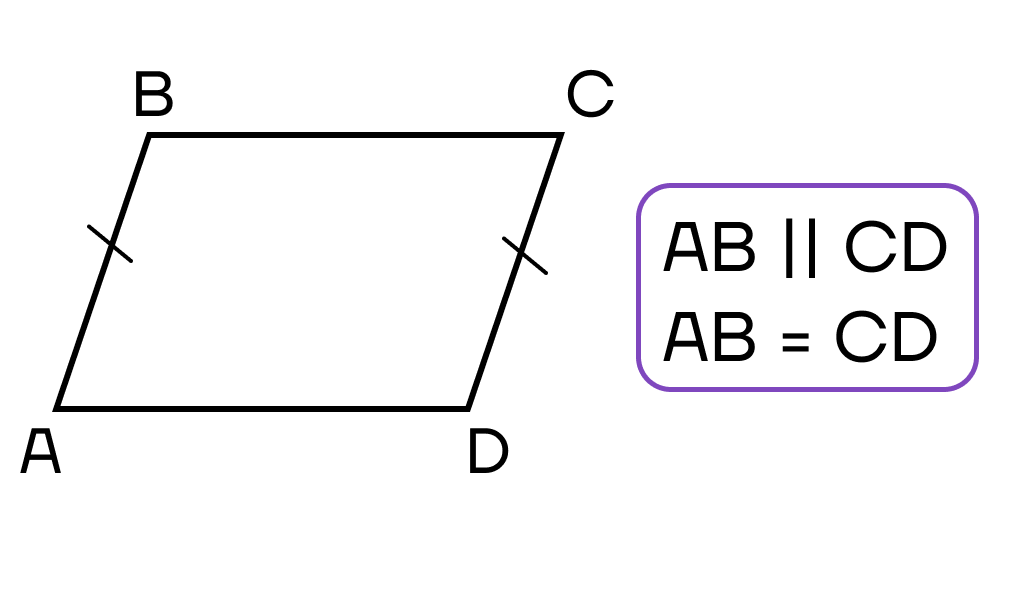
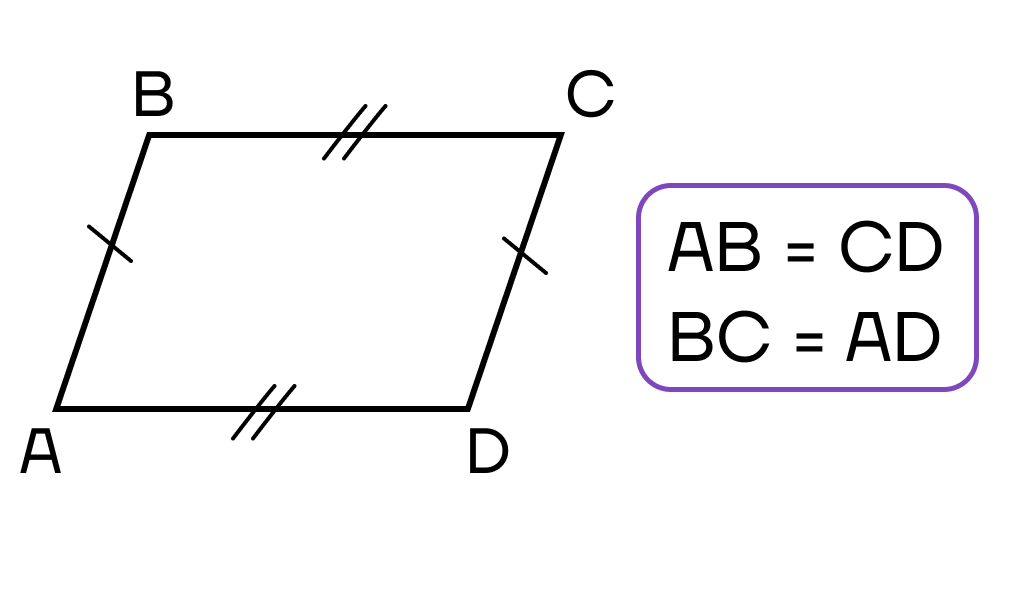
- Противоположные стороны четырехугольника попарно равны.
- Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.

Свойства параллелограмма
Свойства нельзя путать с признаками, хоть они и очень похожи. Свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, тогда как признаки предназначены для выявления параллелограммов среди четырехугольников.
Свойства параллелограмма:
- Противолежащие стороны равны.

- Противолежащие стороны параллельны.
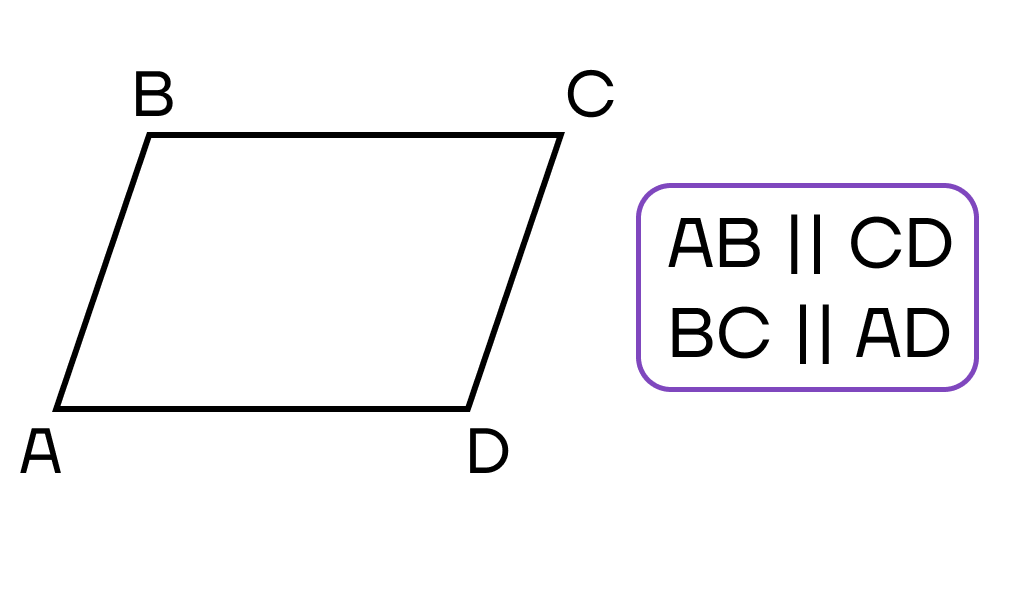
- Противолежащие углы равны.
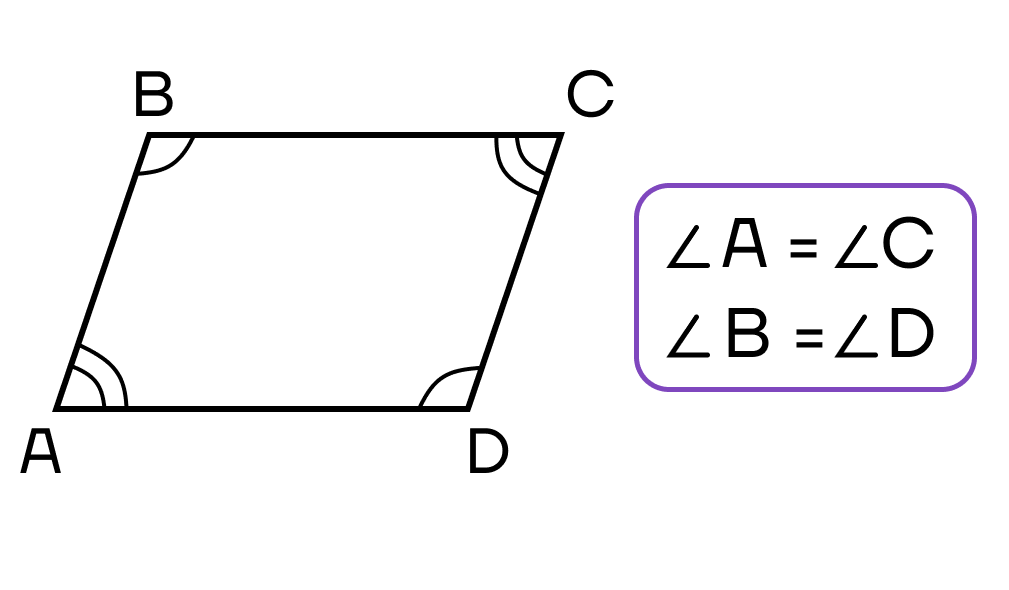
- Сумма всех углов 3600.
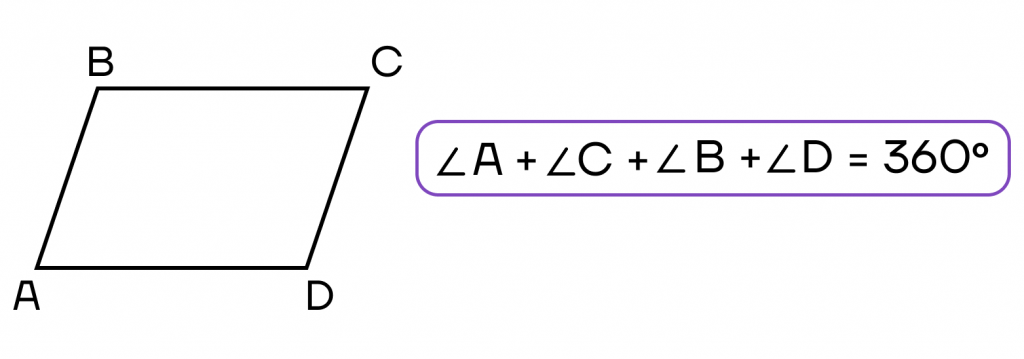
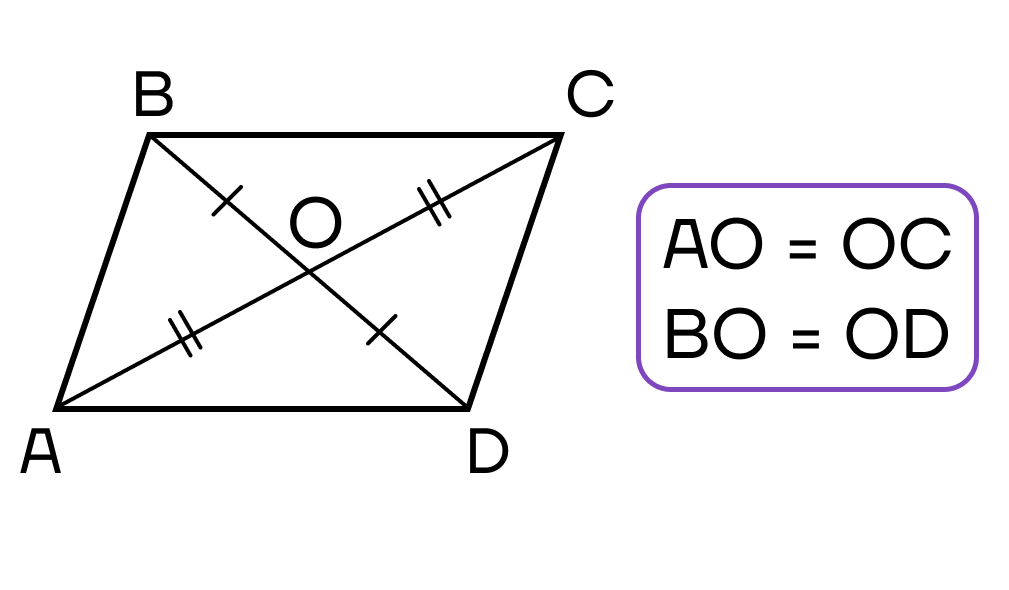
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Сумма углов, прилежащих к любой стороне, равна 1800.
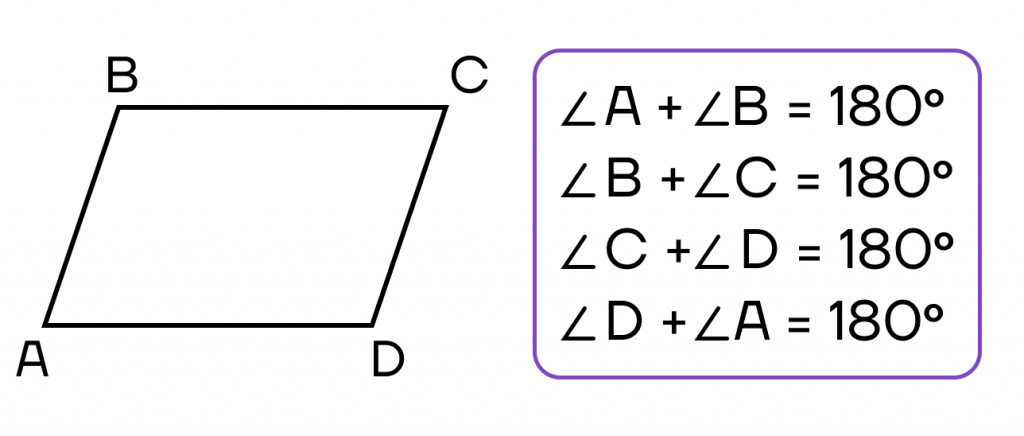
- Сумма квадратов диагоналей равна сумме квадратов всех сторон.
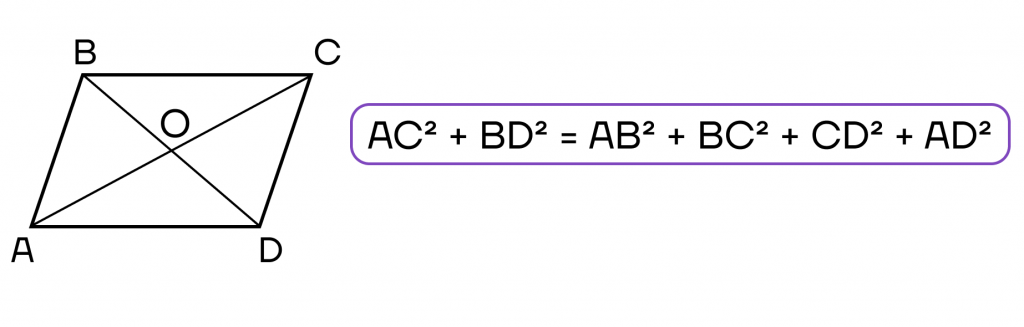
- Диагонали делят параллелограмм на четыре треугольника с одинаковой площадью.

- Каждая диагональ делит параллелограмм на два равных треугольника

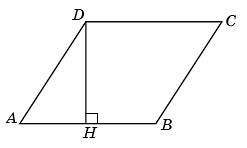
Биссектриса в параллелограмме
Можно ли провести биссектрису в параллелограмме? Да. Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.

Значение биссектрисы легко запомнить, используя фразу “Биссектриса – это крыса, она бегает по углам и делит угол пополам”.
Так как у треугольника три угла – соответственно, и крыс-биссектрис тоже три.
Два факта связанные с биссектрисой в параллелограмме:
- Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник.

- Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.
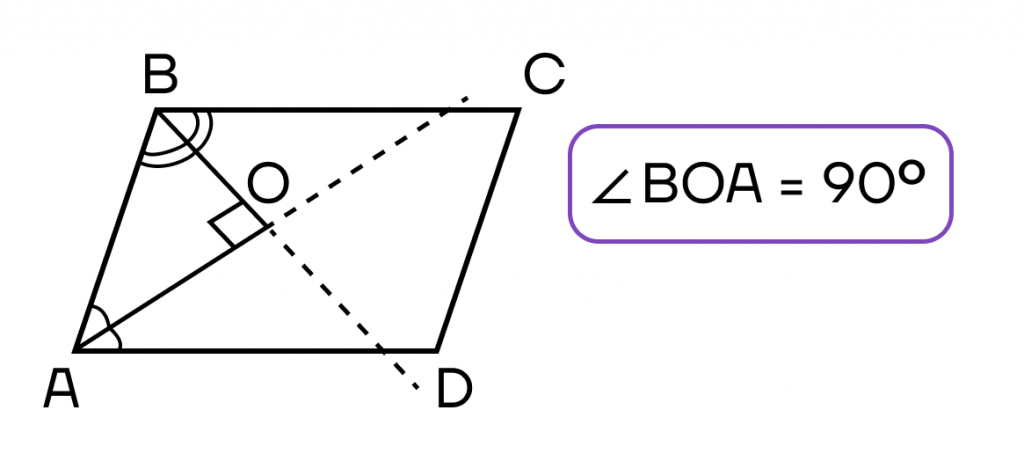
Площадь параллелограмма
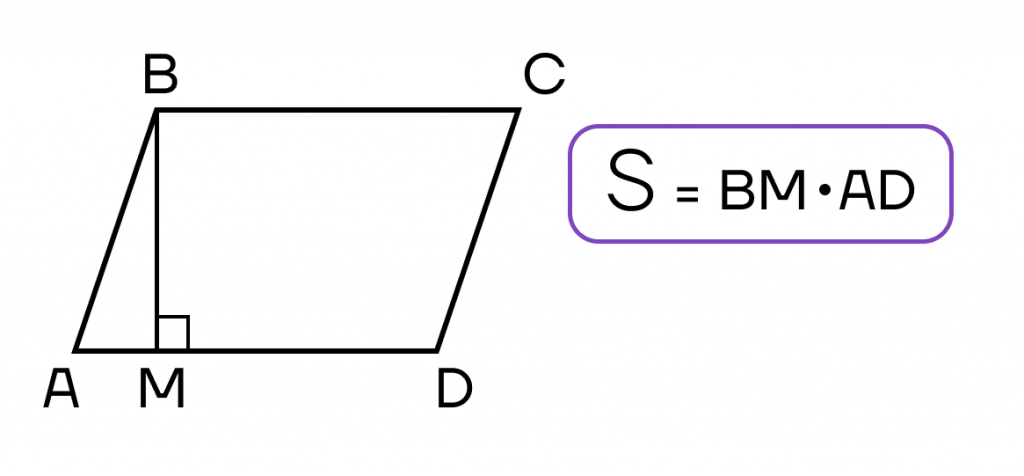
Есть три формулы площади параллелограмма, которые применяются в зависимости от известных величин
- Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
- Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.

- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

Прямоугольник
Как параллелограмм связан с прямоугольником?
Прямоугольник – это параллелограмм, углы которого по 900.
Данную фигуру часто называют частным случаем параллелограмма. Из этого следует, что для прямоугольника применимы те же признаки и свойства, что для параллелограмма, но и имеется ряд собственных.
В жизни прямоугольником можно назвать дверь, картину или фотографию:
Признаки прямоугольника
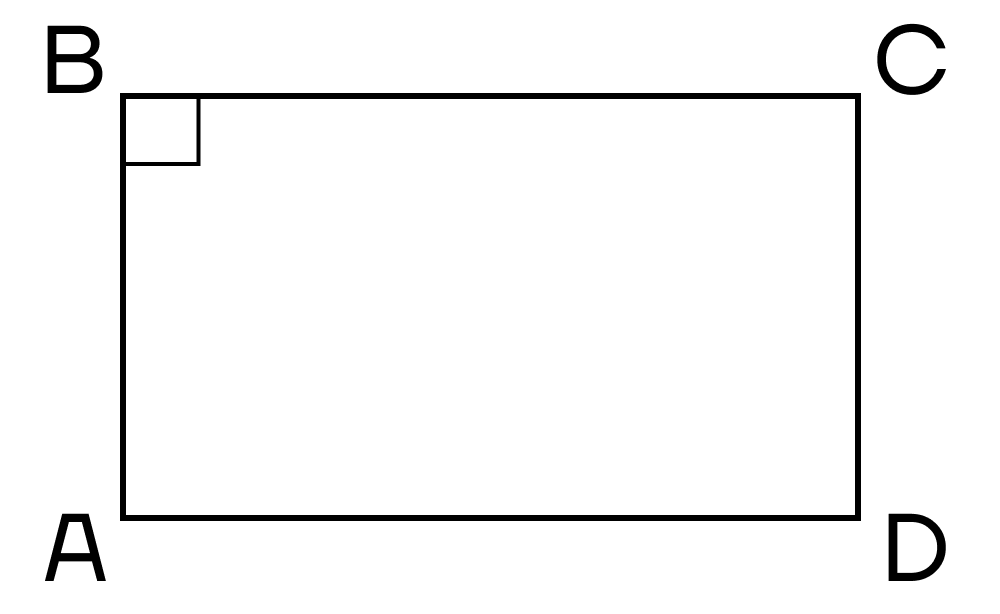
- Параллелограмм, имеющий хотя бы один прямой угол.
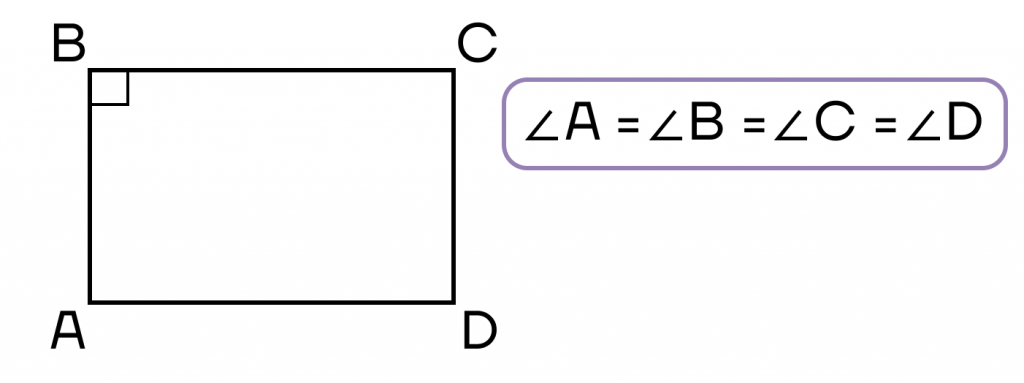
- Параллелограмм, все углы которого равны.
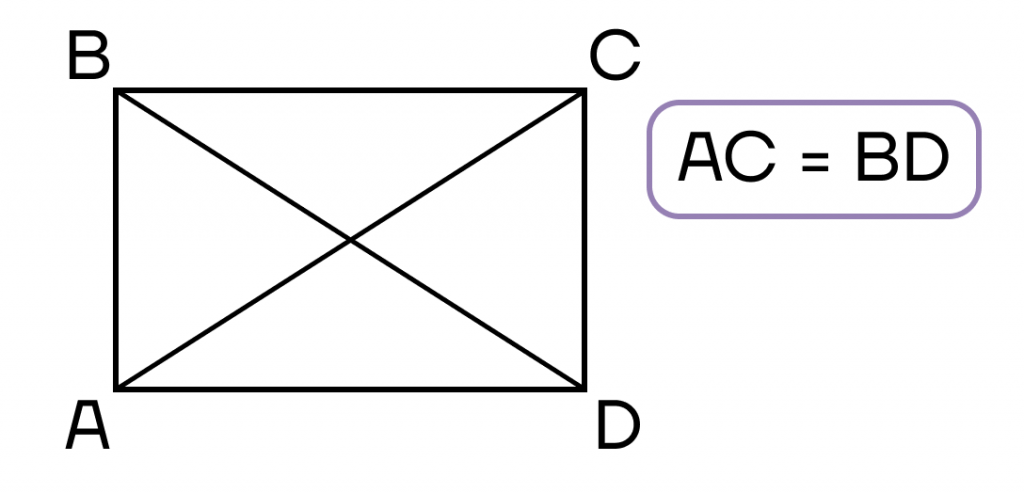
- Параллелограмм, диагонали которого равны.
- Четырехугольник, у которого три прямых угла.

Свойства прямоугольника
- Все углы прямые.

- Диагонали равны.

- Стороны прямоугольника одновременно являются и его высотами.
- Сумма квадратов двух прилежащих сторон равна квадрату диагонали.
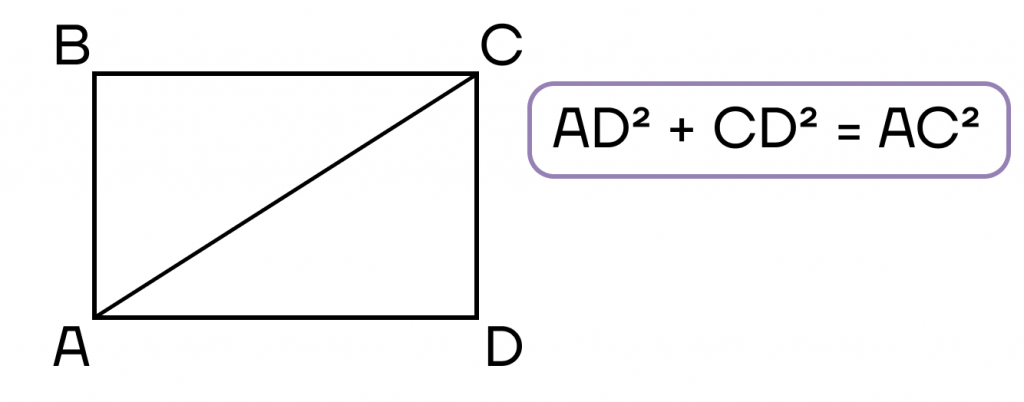
Биссектриса и площадь прямоугольника
Биссектриса делит угол прямоугольника на два угла по 450 и пересекает одну из сторон прямоугольника.
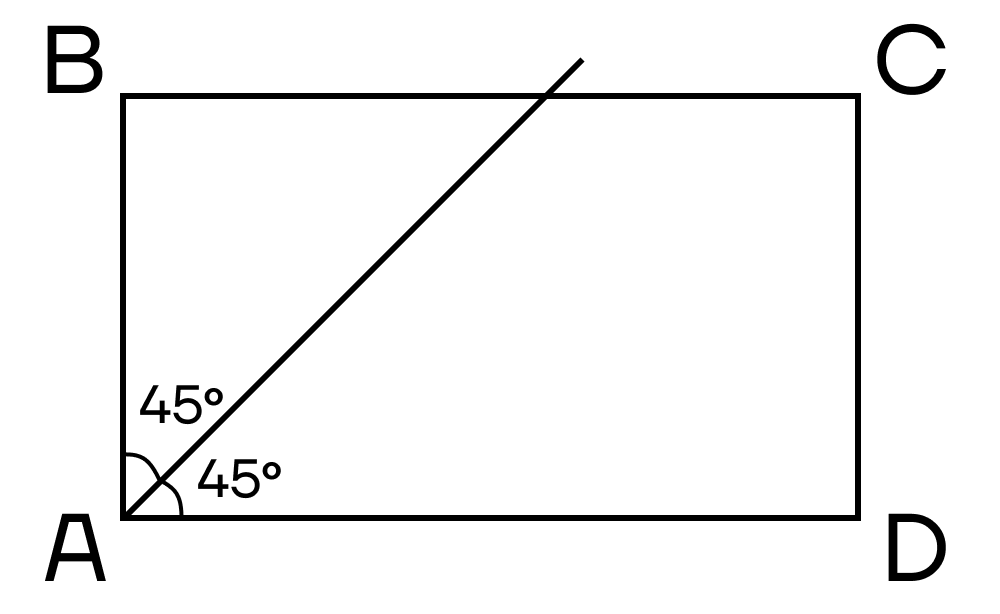
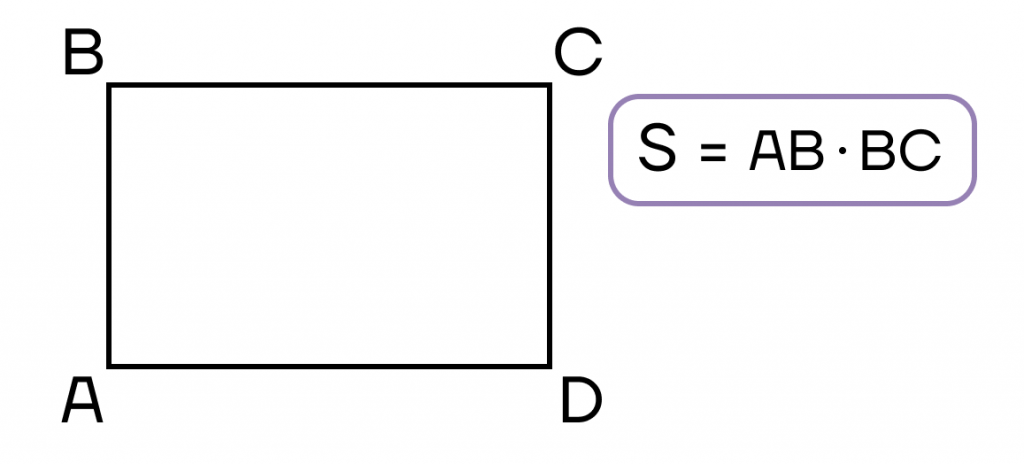
Теперь рассмотрим два способа нахождения площади прямоугольника:
- Площадь прямоугольника равна произведению двух соседних сторон.
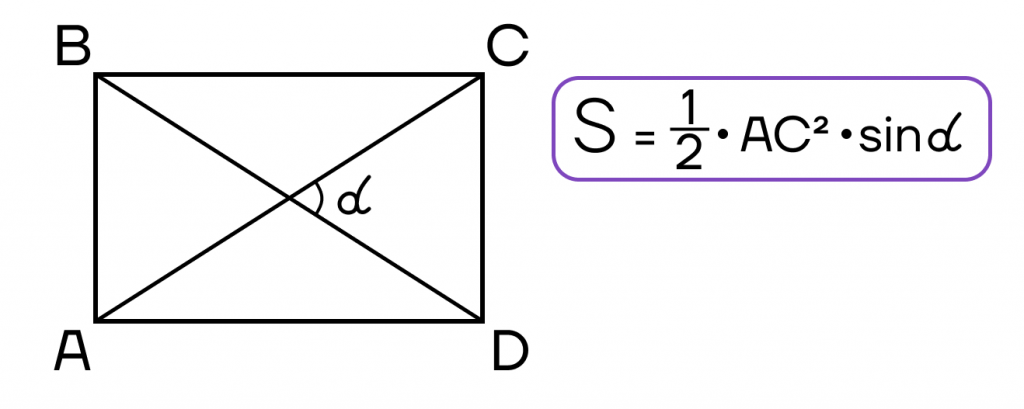
- Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между диагоналями.
Ромб
Пожалуй, это самая неустойчивая фигура.

Ромб – это параллелограмм, у которого все стороны равны.

Ромб можно увидеть на знаке машины “Митсубиси”, их там целых три.
А также в игровых наградах:

Также является частным случаем параллелограмма и обладает его признаками и свойствами, но имеет и собственные.
Всё о ромбе
Признаки ромба:
- Две смежные стороны параллелограмма равны.
- Диагонали параллелограмма пересекаются под прямым углом.
- Диагональ параллелограмма делит каждый угол пополам.
- Четырехугольник, у которого все стороны равны.
Свойства ромба:
- Все стороны равны.

- Диагонали пересекаются под прямым углом и точкой пересечения делятся пополам.

- Диагонали являются биссектрисами.

- Высоты в ромбе равны.
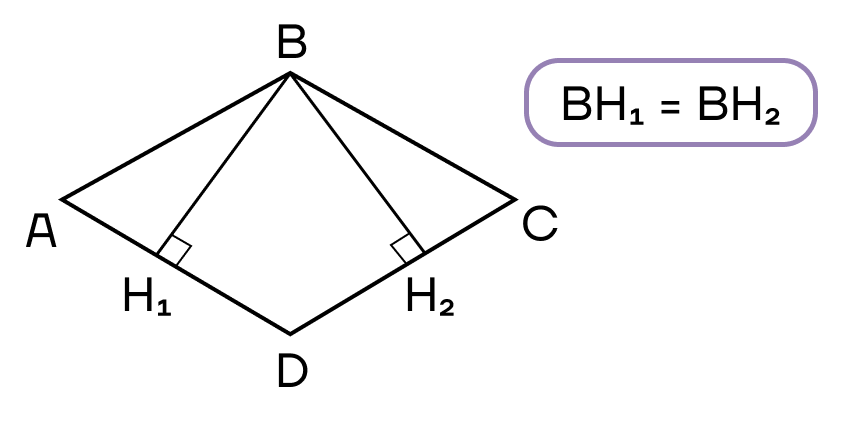
Как уже отмечено в свойствах ромба, биссектрисой ромба является диагональ.
Как найти площадь ромба?
Для нахождения площади ромба есть три разные формулы:
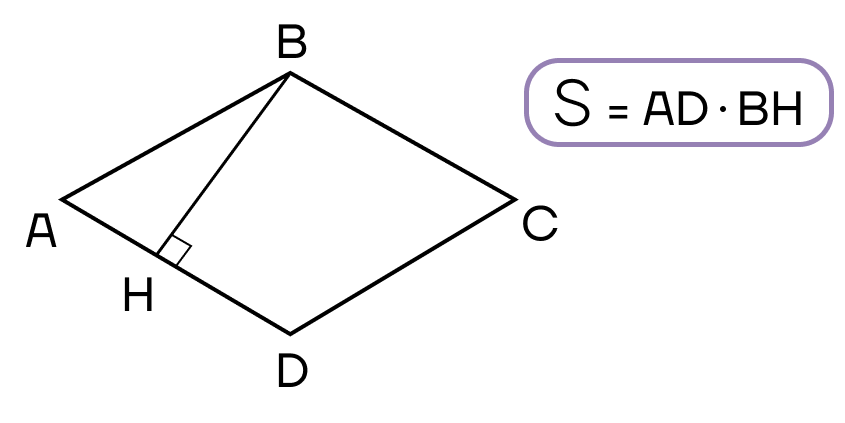
- Площадь ромба равна произведению стороны и высоты ромба.
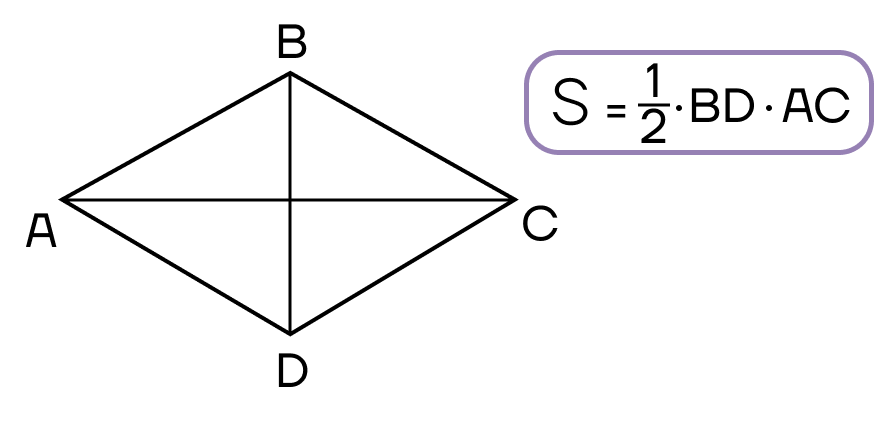
- Площадь ромба равна половине произведения его диагоналей.
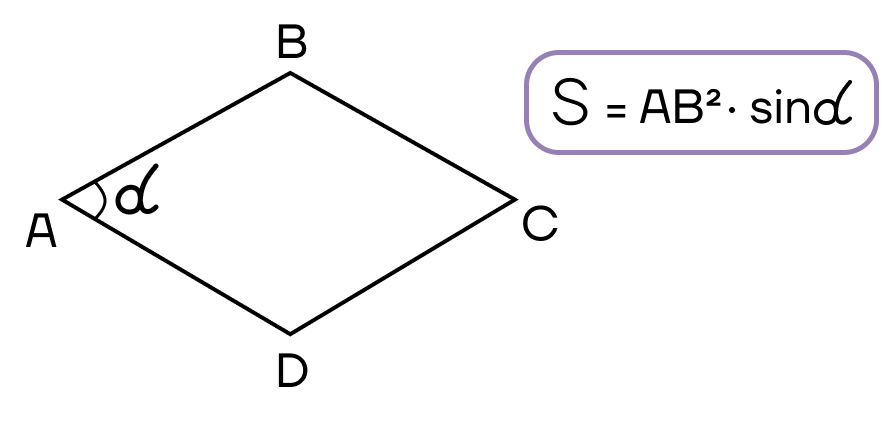
- Площадь ромба равна произведению квадрата стороны на синус угла ромба.
Квадрат
А вот квадрат, наоборот, достаточно устойчив.

Квадрат – это четырехугольник, у которого все углы и стороны равны.
Если внимательно посмотреть на определение, то можно заметить, что квадрат объединяет в себе и параллелограмм, и прямоугольник, и ромб.
Нечто, сочетающее в себе разнородные элементы, называют гибридом. Квадрат будет иметь все признаки и свойства родительских фигур:параллелограмма, прямоугольника и ромба.

Квадратом может быть крышка подарочной коробки или окно.


Рассмотрим признаки и свойства данной фигуры.
Всё о квадрате
Признаки квадрата:
- Ромб, у которого хотя бы один угол прямой.
- Ромб, у которого все углы равны.
- Ромб, у которого диагонали равны.
- Четырехугольник, диагонали которого равны и перпендикулярны.
Свойства квадрата:
- Диагональ квадрата равна 2 стороны квадрата.
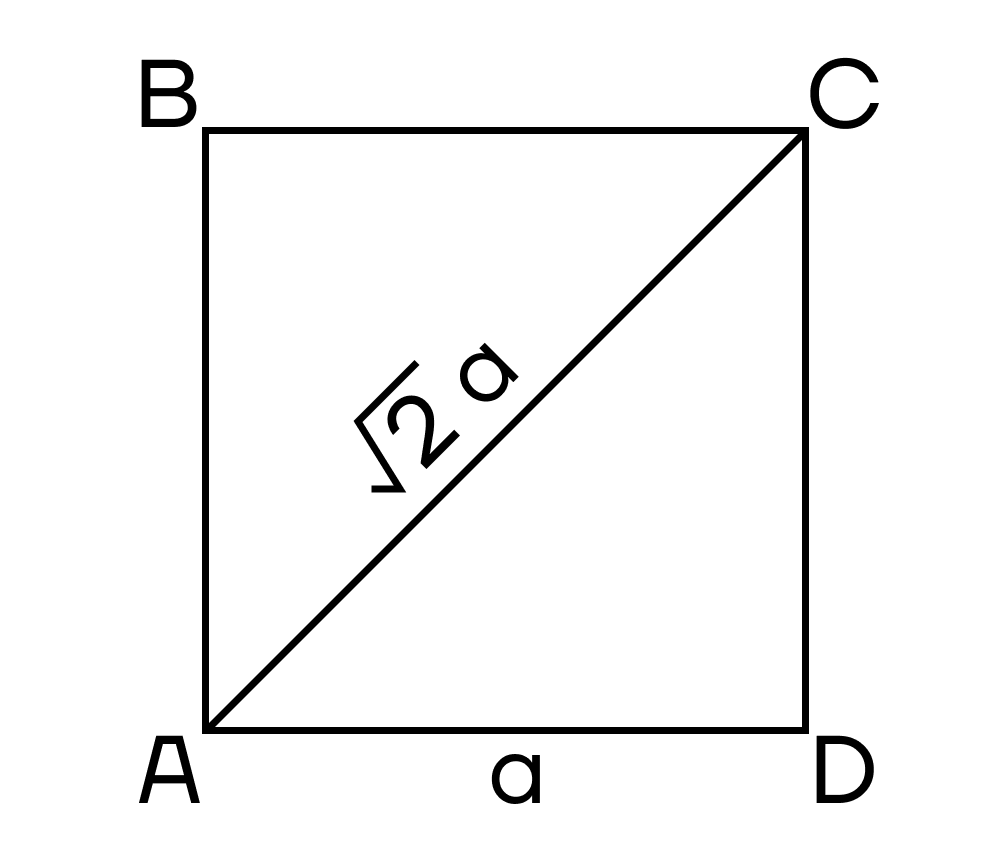
- Диагонали делят квадрат на четыре равных треугольника.

Биссектрисой квадрата, как и у ромба, является диагональ.
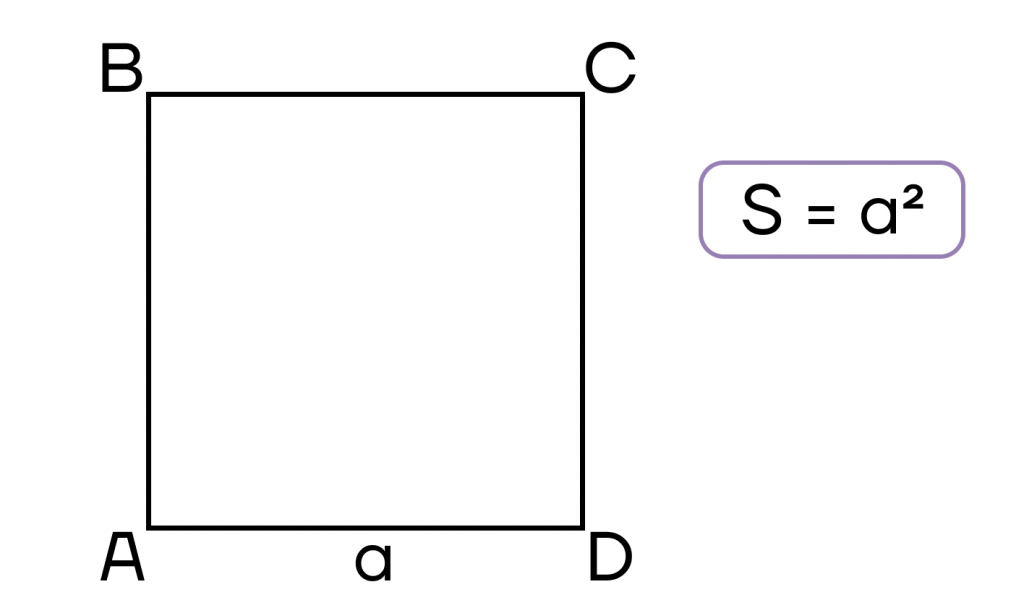
Рассмотрим формулы для нахождения площади квадрата:
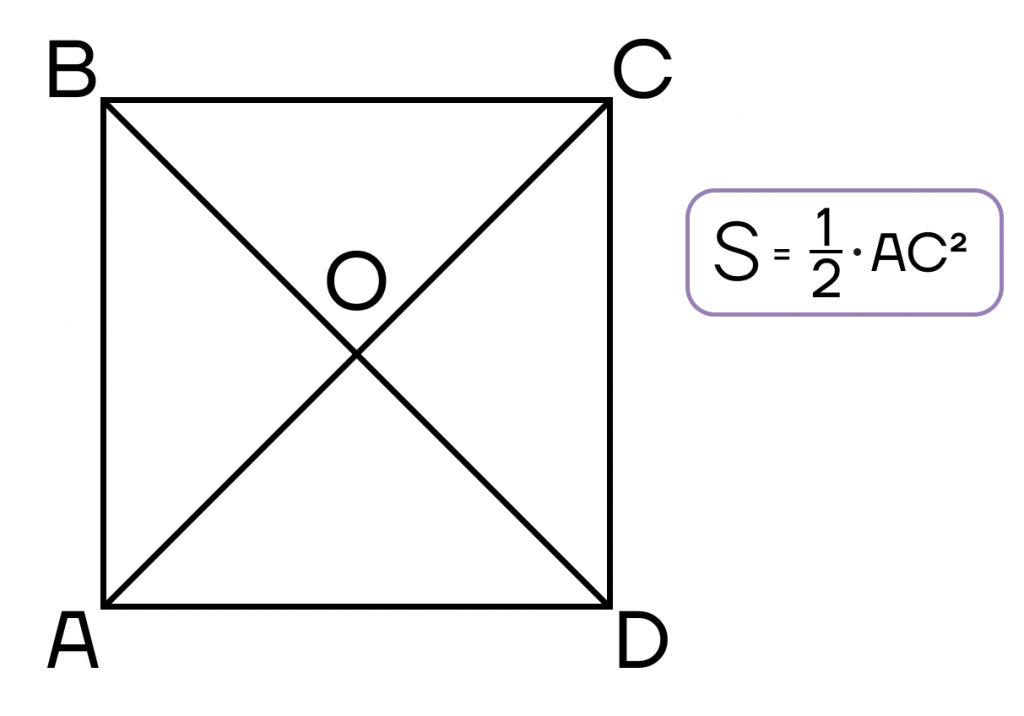
- Площадь квадрата равна квадрату его стороны.
- Площадь квадрата равна половине квадрата диагонали.
Фактчек
- Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.
- Прямоугольник – это параллелограмм, углы которого по 900 и диагонали которого равны.
- Ромб – это параллелограмм, у которого все стороны равны, а также диагонали перпендикулярны друг другу
- Квадрат – это четырехугольник, у которого все углы и стороны равны. Квадрат является гибридом параллелограмма, прямоугольника и ромба.
Проверь себя
Задание 1.
Найдите площадь параллелограмма, если его стороны 5 и 8, а угол между ними 300
- 40
- 20
- 10
- 25
Задание 2.
Найдите площадь прямоугольника, если его диагональ 12, а угол между диагоналями 600
- 83
- 6
- 63
- 4
Задание 3.
Найдите площадь ромба, если его диагонали 6 и 10
- 30
- 60
- 15
- 25
Задание 4.
У четырехугольника диагонали пересекаются под углом 300, а его стороны попарно параллельны и равны. Что это за фигура?
- Квадрат
- Ромб
- Прямоугольник
- Параллелограмм
Задание 5.
У четырехугольника две противоположные стороны параллельны и равны и есть один прямой угол. Что это за фигура?
- Квадрат
- Ромб
- Прямоугольник
- Параллелограмм
Ответы: 1. – 2; 2. – 3; 3. – 1; 4. – 4; 5. – 3



