Как найти площадь параллелограмма через косинус угла

Как найти площадь параллелограмма через косинус угла

Площадь параллелограмма через сторону и высоту

{S = a cdot h}

Найти площадь параллелограмма

На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные – основание, высоту, стороны, диагонали и углы между ними и получите ответ.

Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).

Содержание:
  1. калькулятор площади параллелограмма
  2. формула площади параллелограмма через сторону и высоту
  3. формула площади параллелограмма через две стороны и угол между ними
  4. формула площади параллелограмма через диагонали и угол между ними
  5. примеры задач

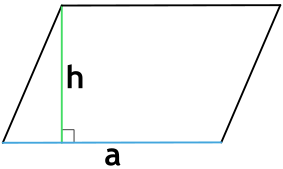
Формула площади параллелограмма через сторону и высоту

Площадь параллелограмма через сторону и высоту

{S = a cdot h}

a – сторона параллелограмма

h – высота параллелограмма

Формула площади параллелограмма через две стороны и угол между ними

Площадь параллелограмма через две стороны и угол между ними

{S=a cdot b cdot sin(alpha)}

a, b – стороны параллелограмма

α – угол между сторонами a и b

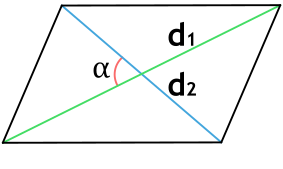
Формула площади параллелограмма через диагонали и угол между ними

Площадь параллелограмма через диагонали и угол между ними

{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}

d1, d2 – диагонали параллелограмма

α – угол между диагоналями

Примеры задач на нахождение площади параллелограмма

Задача 1

Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.

Решение

Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.

S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2

Ответ: 108 cdot 0.866 approx 93.53074 : см^2

Мы можем проверить ответ с помощью калькулятора .

Задача 2

Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.

Решение

Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.

S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2

Ответ: 48 см²

И снова проверить ответ нам поможет калькулятор .

Задача 3

Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.

Решение

В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.

S = a cdot h = 12 cdot 8 = 96 : см^2

Ответ: 96 см²

И снова проверить ответ нам поможет калькулятор .

Источник

Площадь параллелограмма можно найти по стороне и проведённой к этой стороне высоте, по двум сторонам и углу, по диагоналям и углу между ними.

 I. Площадь параллелограмма по стороне и высоте

Площадь параллелограмма равна произведению стороны параллелограмма на высоту, проведённую к этой стороне.

Формула для нахождения площади параллелограмма через сторону и высоту:

    [S = a cdot {h_a}]

ploshchad-parallelogrammaНапример,площадь параллелограмма ABCD через высоту можно найти по одной из формул:

    [{S_{ABCD}} = AD cdot BF]

или

ploshchad-parallelogramma-cherez-vysotu

    [{S_{ABCD}} = CD cdot BK]

II. Площадь параллелограмма по сторонам и углу

Площадь параллелограмма равна произведению его сторон на синус угла между ними.

Формула для нахождения площади параллелограмма через стороны и угол:

    [S = absin alpha ]

ploshchad-parallelogramma-po-storonam-i-ugluНапример, площадь параллелограмма ABCD

    [{S_{ABCD}} = AD cdot AB cdot sin angle BAD]

По свойствам параллелограмма, противоположные углы параллелограмма равны:

    [angle A = angle C]

    [angle B = angle D]

Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º, то есть,

    [angle B = {180^o} - angle A]

    [angle D = {180^o} - angle A]

А так как синус тупого угла равен синусу смежного ему угла, то

    [sin angle B = sin ({180^o} - angle A) = sin angle A]

    [sin angle D = sin ({180^o} - angle A) = sin angle A]

Таким образом, площадь параллелограмма можно найти как произведение его двух любых не смежных сторон на синус любого угла.

III. Площадь параллелограмма по диагоналям

Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.

Формула площади параллелограмма через диагонали:

    [S = frac{1}{2}{d_1} cdot {d_2} cdot sin varphi ]

ploshchad-parallelogramma-po-diagonalyamНапример, площадь параллелограмма ABCD

    [{S_{ABCD}} = frac{1}{2}AC cdot BD cdot sin angle COD]

А так как

    [sin angle AOD = sin ({180^o} - angle COD) = sin angle COD,]

то в качестве угла между диагоналями можно брать любой угол — как острый, так и тупой (прямой — в ромбе и квадрате).

Источник

как найти площадь параллелограмма, если известны стороны и косинус между ними??

Вячеслав Зайцев



Ученик

(231),
на голосовании



10 лет назад

Голосование за лучший ответ

Натали

Мастер

(1375)


10 лет назад

А синус найдете как синус квадрат альфа плюс косинус квадрат альфа равно единица

Источник: удачи:)

Похожие вопросы

Источник

Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.

  • Формула вычисления площади

    • По длине стороны и высоте

    • По двум сторонам и углу между ними

    • По двум диагоналям и углу между ними

  • Примеры задач

Формула вычисления площади

По длине стороны и высоте

Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:

S = a ⋅ h

Площадь параллелограмма

По двум сторонам и углу между ними

Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:

S = a ⋅ b ⋅ sin α

Площадь параллелограмма

По двум диагоналям и углу между ними

Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:

S = 1/2 ⋅ d 1 ⋅ d 2 ⋅ sin α

Площадь параллелограмма

Примеры задач

Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.

Решение:
Используем первую формулу, в которой задействованы известные нам по условиям задания значения: S = 4 см * 7 см = 28 см2.

Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.

Решение:
Применим вторую формулу, рассмотренную выше: S = 6 см * 8 см * sin 30° = 24 см2.

Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.

Решение:
Воспользуемся формулой, в которой фигурируют диагонали: S = 1/2 * 4 см * 6  см * sin 90° = 12 см2.

Источник

1. Формула площади параллелограмма через стороны и углы

Формулы параллелограмма

a, b – стороны параллелограмма

α, β – углы параллелограмма

Формула площади через стороны и углы параллелограмма, (S):

Формулы площади параллелограмма

Калькулятор – вычислить, найти площадь параллелограмма:

a(сторона)=

b(сторона)=

α или β (угол в градусах)= ( sin α=sin β )

S=

2. Формула площади параллелограмма через сторону и высоту

Формулы параллелограмма

a, b – стороны параллелограмма

Hb – высота на сторону b

Ha – высота на сторону a

Формула площади через стороны и высоты параллелограмма, (S):

Формулы площади параллелограмма

3. Формула площади параллелограмма через диагонали и угол между ними

Формулы параллелограмма

D – большая диагональ

d –меньшая диагональ

α, β – углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , (S):

Формулы площади параллелограмма

Калькулятор – вычислить, найти площадь параллелограмма:

D (большая диагональ)=

d (меньшая диагональ )=

α или β (угол в градусах)= ( sin α=sin β )

S=

Формулы для параллелограмма:

Как найти стороны параллелограмма

Как найти диагонали параллелограмма

Острый угол и тупой угол параллелограмма

Углы между диагоналями параллелограмма

Формула суммы квадратов диагоналей параллелограмма

Высота параллелограмма и угол пересечения высот

Свойства и длина биссектрисы параллелограмма

Периметр параллелограмма

Все формулы по геометрии

Источник

Добавить комментарий