Площадь параллелограмма при заданной площади длинного диагонального треугольника Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 2D геометрия ↺ | |
| 2D геометрия | Параллелограмм ↺ | |
| Параллелограмм | Площадь параллелограмма ↺ |
|
✖Площадь длинного диагонального треугольника параллелограмма – это площадь плоскости, заключенной в треугольнике, образованном длинной диагональю и парой ребер при тупом углу параллелограмма.ⓘ Площадь длинного диагонального треугольника параллелограмма [Al(Triangle)] |
+10% -10% |
|
✖Площадь параллелограмма — это общее количество плоскостей, ограниченных границей параллелограмма.ⓘ Площадь параллелограмма при заданной площади длинного диагонального треугольника [A] |
⎘ копия |
Площадь параллелограмма при заданной площади длинного диагонального треугольника Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Площадь длинного диагонального треугольника параллелограмма: 30 Квадратный метр –> 30 Квадратный метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
60 Квадратный метр –> Конверсия не требуется
9 Площадь параллелограмма Калькуляторы
Площадь параллелограмма при заданной площади длинного диагонального треугольника формула
Площадь параллелограмма = 2*Площадь длинного диагонального треугольника параллелограмма
A = 2*Al(Triangle)
Что такое параллелограмм?
Параллелограмм — это особый тип четырехугольника, который имеет две пары противоположных и параллельных сторон. Прямоугольники — это особый тип параллелограмма. Углы параллелограмма также попарно равны и противоположны – одна пара равных и противоположных острых углов и одна пара равных и противоположных тупых углов.
Как найти площадь параллелограмма, треугольника, трапеции
Любовь Петровна Гаврилюк
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Площадь параллелограмма
Теорема 1
Площадь параллелограмма определяется как произведение длины его стороны, на высоту, проведенную к ней.
Математически это можно записать следующим образом
[S=ah]
где $a$ сторона параллелограмма, $h$ – высота, проведенная к этой стороне.
Доказательство.
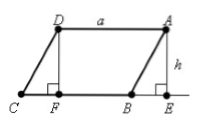
Пусть нам дан параллелограмм $ABCD$, у которого $AD=BC=a$. Проведем высоты $DF$ и $AE$ (рис. 1).
Рисунок 1.
Очевидно, что фигура $FDAE$ — прямоугольник.
[angle BAE={90}^0-angle A, ] [angle CDF=angle D-{90}^0={180}^0-angle A-{90}^0={90}^0-angle A=angle BAE]
Следовательно, так как $CD=AB, DF=AE=h$, по $I$ признаку равенства треугольников $triangle BAE=triangle CDF$. Тогда
[S_{FDAE}=S_{ABCD}-S_{CDF}+S_{BAE}=S_{ABCD}-S_{CDF}+S_{CDF}=S_{ABCD}]
Значит по теореме о площади прямоугольника:
[S_{ABCD}=S_{FDAE}=ah]
Теорема доказана.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Теорема 2
Площадь параллелограмма определяется как произведение длины его смежных сторон, на синус угла между этими сторонами.
Математически это можно записать следующим образом
[S=absinalpha ]
где $a, b$ стороны параллелограмма, $alpha $ — угол между ними.
Доказательство.
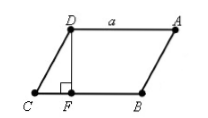
Пусть нам дан параллелограмм $ABCD$, у которого $BC=a, CD=b, angle C=alpha $. Проведем высоту $DF=h$ (рис. 2).
Рисунок 2.
По определению синуса, получим
[sinalpha =frac{DF}{CD}=frac{h}{b}]
Следовательно
[h=bsinalpha ]
Значит, по теореме $1$:
[S=ah=absinalpha ]
Теорема доказана.
Площадь треугольника
Теорема 3
Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней.
Математически это можно записать следующим образом
[S=frac{1}{2}ah]
где $a$ сторона треугольника, $h$ – высота, проведенная к этой стороне.
Доказательство.
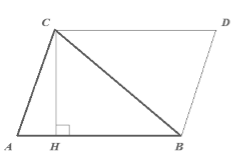
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).
Рисунок 3.
Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда
[S_{ABC}=frac{1}{2}S_{ABCD}]
Значит по теореме $1$:
[S_{ABC}=frac{1}{2}ah]
Теорема доказана.
«Как найти площадь параллелограмма, треугольника, трапеции» 👇
Теорема 4
Площадь треугольника определяется как половина произведения длины его смежных сторон, на синус угла между этими сторонами.
Математически это можно записать следующим образом
[S=frac{1}{2}absinalpha ]
где $a, b$ стороны треугольника, $alpha $ — угол между ними.
Доказательство.
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).
Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда
[S_{ABC}=frac{1}{2}S_{ABCD}]
Значит по теореме $1$:
[S_{ABC}=frac{1}{2}absinalpha ]
Теорема доказана.
Площадь трапеции
Теорема 5
Площадь трапеции определяется как половина произведения суммы длин его оснований, на его высоту.
Математически это можно записать следующим образом
[S=frac{1}{2}(a+b)h]
Доказательство.
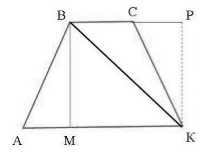
Пусть нам дана трапеция $ABCK$, где $AK=a, BC=b$. Проведем в ней высоты $BM=h$ и $KP=h$, а также диагональ $BK$ (рис. 4).
Рисунок 4.
[S_{ABCK}=S_{ABK}+S_{BCK}]
По теореме $3$, получим
[S_{ABK}=frac{1}{2}AKcdot BM=frac{1}{2}ah, S_{BCK}=frac{1}{2}BCcdot KP=frac{1}{2}bh]
Тогда
[S_{ABCK}=frac{1}{2}ah+frac{1}{2}bh=frac{1}{2}(a+b)h]
Теорема доказана.
Пример задачи
Пример 1
Найти площадь равностороннего треугольника, если длина его стороны равняется $a.$
Решение.
Так как треугольник равносторонний, то все его углы равняются ${60}^0$.
Тогда, по теореме $4$, имеем
[S=frac{1}{2}acdot acdot sin{60}^0=frac{a^2sqrt{3}}{4}]
Ответ: $frac{a^2sqrt{3}}{4}$.
Заметим, что результат этой задачи можно применять при нахождении площади любого равностороннего треугольника с данной стороной.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 19.05.2022
Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.
Онлайн-калькулятор площади параллелограмма
Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.
Рассмотрим несколько способов и формул с последующим решением простых примеров.
Формула площади параллелограмма по основанию и высоте
Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением. Для начала разберем обобщенный случай без использования чисел.
Пусть дан произвольный параллелограмм с основанием aa, боковой стороной bb и высотой hh, проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:
S=a⋅hS=acdot h
aa — основание;
hh — высота.
Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.
Найти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).
Решение
a=10a=10
h=5h=5
Подставляем в нашу формулу. Получаем:
S=10⋅5=50S=10cdot 5=50 (см. кв.)
Ответ: 50 (см. кв)
Формула площади параллелограмма по двум сторонам и углу между ними
В этом случае искомая величина находится так:
S=a⋅b⋅sin(α)S=acdot bcdotsin(alpha)
a,ba, b — стороны параллелограмма;
αalpha — угол между сторонами aa и bb.
Теперь решим другой пример и воспользуемся вышеописанной формулой.
Найти площадь параллелограмма если известна сторона aa, являющаяся основанием и с длиной 20 (см.) и периметр pp, численно равный 100 (см.), угол между смежными сторонами (aa и bb) равен 30 градусам.
Решение
a=20a=20
p=100p=100
α=30∘alpha=30^{circ}
Для нахождения ответа нам неизвестна лишь вторая сторона данного четырехугольника. Найдем ее. Периметр параллелограмма дается формулой:
p=a+a+b+bp=a+a+b+b
100=20+20+b+b100=20+20+b+b
100=40+2b100=40+2b
60=2b60=2b
b=30b=30
Самое сложное позади, осталось только подставить наши значения для сторон и угла между ними:
S=20⋅30⋅sin(30∘)=300S=20cdot 30cdotsin(30^{circ})=300 (см. кв.)
Ответ: 300 (см. кв.)
Формула площади параллелограмма по диагоналям и углу между ними
S=12⋅D⋅d⋅sin(α)S=frac{1}{2}cdot Dcdot dcdotsin(alpha)
DD — большая диагональ;
dd — малая диагональ;
αalpha — острый угол между диагоналями.
Даны диагонали параллелограмма, равные 10 (см.) и 5 (см.). Угол между ними 30 градусов. Вычислить его площадь.
Решение
D=10D=10
d=5d=5
α=30∘alpha=30^{circ}
S=12⋅10⋅5⋅sin(30∘)=12.5S=frac{1}{2}cdot 10 cdot 5 cdotsin(30^{circ})=12.5 (см. кв.)
Ответ: 12.5 (см. кв.)
Решение контрольной работы по геометрии онлайн – от профильных экспертов Студворк!
Тест по теме «Площадь параллелограмма»
Необходимо определить, что такое высота параллелограмма.
Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону. Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.
Высота (BE), проведённая между длинными сторонами, короче высоты (BF), проведённой между короткими сторонами.
Так как стороны ромба одинаковы, то высоты ромба также одинаковы: (BE = BF).

Площадь произвольного параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
Проведём высоты из двух вершин (B) и (C) к стороне (AD) .
Прямоугольные треугольники (ABE) и (DCF) равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
Параллелограмм (ABCD) и прямоугольник (EBCF) — равновеликие, так как состоят из равных фигур:
SABCD=SABE+SEBCD;SEBCF=SEBCD+SDCF.
Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
SEBCF=BE⋅BC;SABCD=BE⋅BC=BE⋅AD.
Если обозначить сторону через (a), высоту — через (h), то:
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.
.
Формула определения площади ромба:
Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.
Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали:
Площадь произвольного треугольника
Так как диагональ параллелограмма делит его на два равных треугольника, то площадь треугольника равна половине площади параллелограмма.
, где (h) — высота (на рисунке — (BE)), проведённая к стороне (a) (на рисунке — (AD)).
Для определения площади треугольника можно использовать любую сторону и высоту, проведённую к этой стороне.
Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.
SΔ=pp−ap−bp−c;p=a+b+c2
— формула Герона, где (a), (b) и (c) — стороны треугольника, (p) — полупериметр треугольника.
Площадь прямоугольного треугольника
Так как катеты прямоугольного треугольника взаимно перпендикулярны, то один катет может быть высотой, а другой катет — стороной, к которой проведена высота. Получаем формулу:
S=a⋅b2, где (a) и (b) — катеты.
Для прямоугольного треугольника также можно применять формулы площади произвольного треугольника.
Пример:
1. вычислим площадь треугольника со сторонами (17) см, (39) см, (44) см.
Решение:
p=17+39+442=50;SΔ=50⋅50−17⋅50−39⋅50−44=50⋅33⋅11⋅6==25⋅2⋅3⋅11⋅11⋅2⋅3=5⋅2⋅3⋅11=330см2.
Чтобы легче было вычислить корень, необходимо не перемножать все числа, а раскладывать их на множители:
a⋅a=a
.
Формулу Герона можно использовать для вычисления высоты треугольника.
Пример:
2. вычислим меньшую высоту треугольника, стороны которого равны (15) см, (13) см, (4) см.
Решение:
используем две формулы вычисления площади:
SΔ=aha2
и
SΔ=pp−ap−bp−c
.
Меньшая высота в треугольнике — та, которая проведена к большей стороне, поэтому (a =) (15) см.
.
15⋅h2=24⋅215⋅h=48;h=4815=3,2(см).
Иногда формула Герона используется для вычисления площади параллелограмма, если даны стороны параллелограмма и его диагональ.
Пример:
3. дан параллелограмм со сторонами (17) см и (39) см, длина диагонали равна (44) см. Вычислим площадь параллелограмма.
Решение:
диагональ делит параллелограмм на два равных треугольника. Используем результат, полученный в первом примере:
.
Трапеция имеет одну пару параллельных сторон, следовательно, имеет одну высоту — перпендикуляр, проведённый между параллельными сторонами.
Чаще всего высоту трапеции проводят из вершин или через точку пересечения диагоналей.
Площадь трапеции определим как сумму площадей треугольников, на которые трапецию делит диагональ.
SABCD=SABD+SDBC;SABCD=AD⋅BE2+BC⋅DF2=AD⋅BE2+BC⋅BE2==AD+BC⋅BE2.
Если обозначить параллельные стороны (основания) трапеции через (a) и (b), высоту через (h), то:
Обрати внимание!
Важные следствия:
1. если высоты треугольников равны, то их площади относятся как длины оснований.
2. Если основания треугольников равны, то их площади относятся как длины высот.
3. Если высоты треугольников равны и их основания равны, то они равновелики, например, медиана делит треугольник на две равновеликие части.
1. Формула площади параллелограмма через стороны и углы
a, b – стороны параллелограмма
α, β – углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):
Калькулятор – вычислить, найти площадь параллелограмма:
a(сторона)=
b(сторона)=
α или β (угол в градусах)= ( sin α=sin β )
S=
2. Формула площади параллелограмма через сторону и высоту
a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D – большая диагональ
d –меньшая диагональ
α, β – углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
Калькулятор – вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии