Как найти площадь параллелограмма через синус угла

Формулы площадей через синус угла

Основные свойства площадей фигур:

1. Равные фигуры имеют равные площади.     Две фигуры состоящие   из одинаковых кусков – равновеликие.
2. Аддитивность:   Площадь фигуры, разрезанной на несколько частей, равна сумме площадей этих частей    ;
3. Площадь прямоугольника равна произведению ширины на длину … произведение сторон.

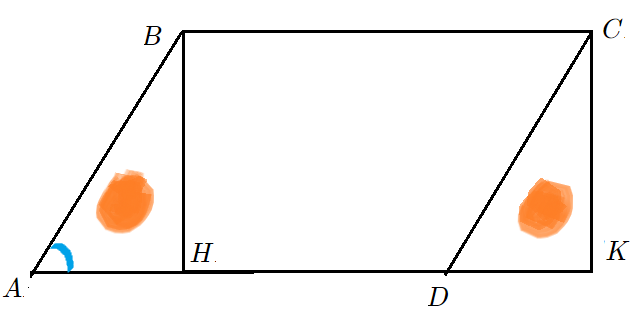
Задача 1:        В параллелограмме известны стороны    $7$,   $10$     и синус угла между ними   $frac{1}{2}$.   Найти площадь параллелограмма.

• Решение:       Опустим высоты $BH$ и $CK$   на основание $AD$ . Они помогут “увидеть” площадь.
• Что есть синус $angle BAH$ в прямоугольном треугольнике $bigtriangleup ABH$?    Отношение катета $BH$ к гипотенузе $AB$.     
• Формула синуса     позволит выразить высоту $BH$ через сторону $AB$ и синус $frac{1}{2}$. Высота   $CK$ такая же.
• Параллелограмм $ABCD$ состоит из кусков:    $bigtriangleup ABH$ и $4$-угольник $HBCD$.   Площадь – сумма площадей кусков.
• Прямоугольник $HBCK$ состоит из кусков $HBCD$ и $bigtriangleup DCK$. Площадь также “сумма кусков”.
• Треугольники $bigtriangleup ABH$ и   $bigtriangleup DCK$ одинаковые. Значит, параллелограмм и прямоугольник равновеликие.
• Площадь Параллелограмма $ABCD$ так же, как прямоугольника $HBCD$ равна высота на основание.
• $S_{ABCD}=S_{ABH}+S_{HBCD}=S_{HBCD}+S_{DCK}=S_{HBCK}=BHcdot HK=ABcdotsin angle BADcdot AD=7cdotfrac{1}{2}cdot10$

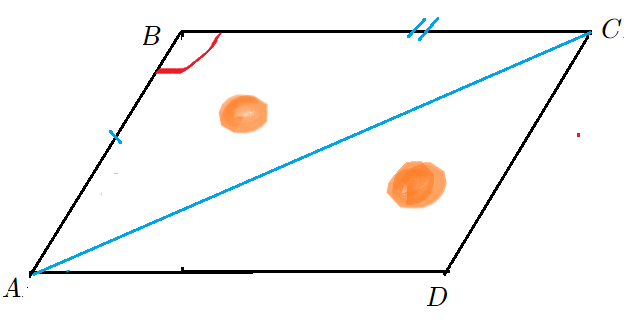
Теорема “о площади параллелограмма и треугольника через синус угла”:

1. Площадь параллелограмма     равна   произведению   сторон   на синус угла параллелограмма:
2. Формулы                  $S=acdot bcdotsin angle BAD$                    $S_{ABCD}=ABcdot BCcdotsin D$
3. Площадь треугольника     равна     половине произведения   сторон треугольника   на   синус угла между ними.
4. Формулы                   $S=frac{1}{2}cdot acdot bcdotsin angle C$                    $S_{bigtriangleup ABC}=frac{1}{2}cdot ABcdot BCcdotsin angle CBA$

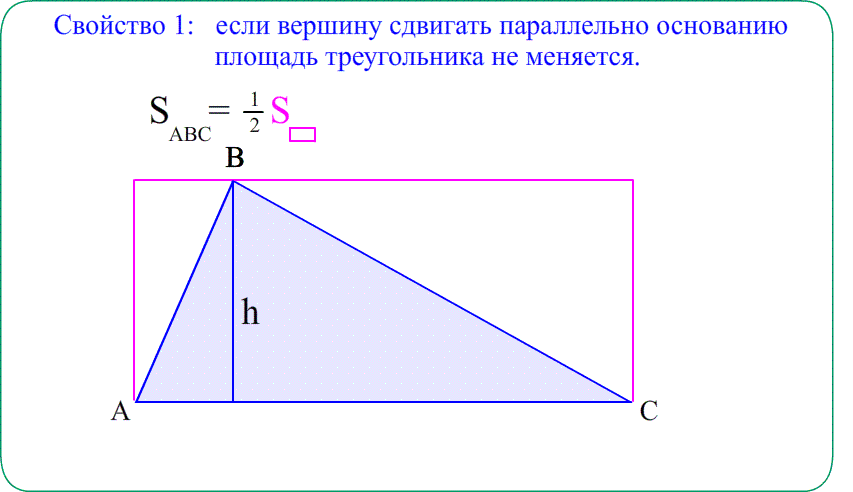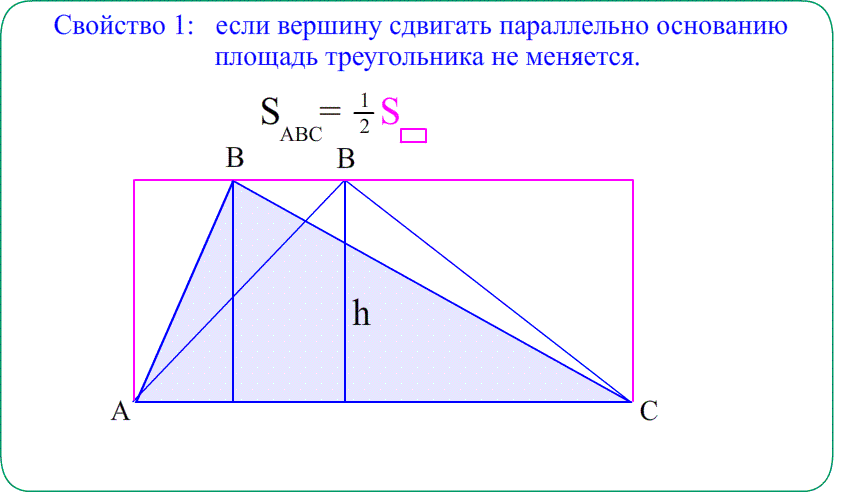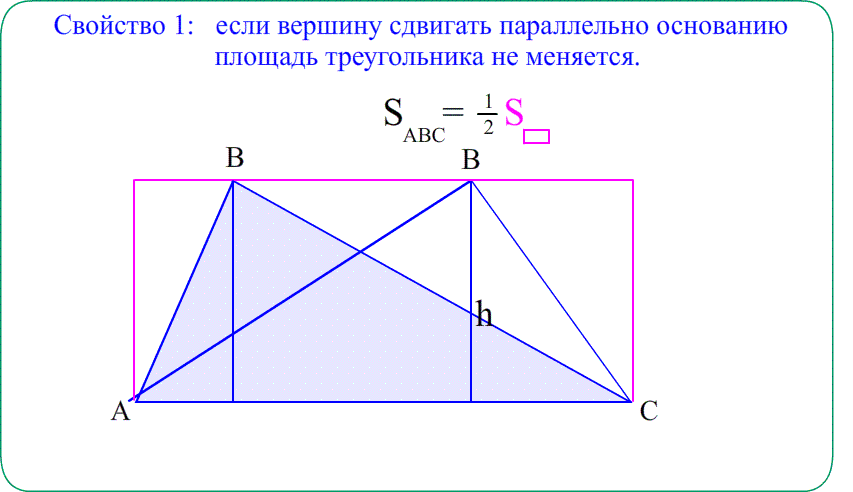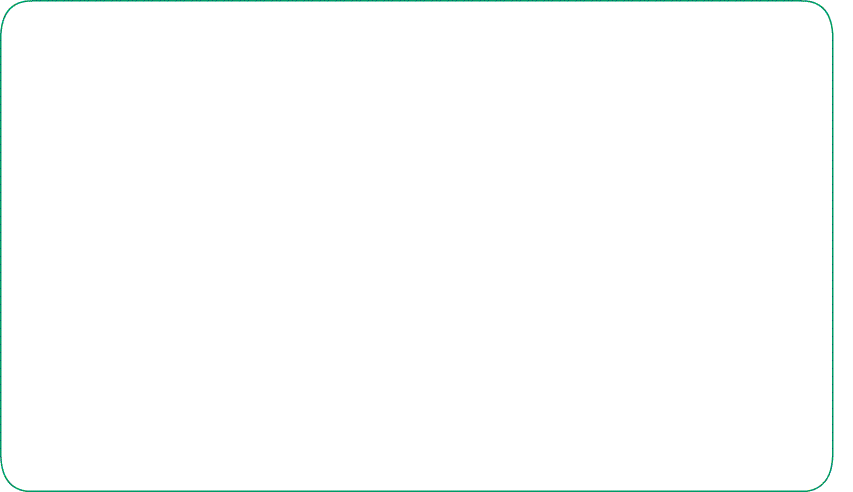
Площадь треугольника также легко получить через площадь параллелограмма, равновеликого с двумя треугольниками, приставленными друг к другу по диагонали. Тогда площадь одного треугольника будет равна половине площади параллелограмма с тем же основанием и с той же высотой.

Задача 2:        Диагонали четырехугольника делятся точкой пересечения на отрезки $3$,   $5$ и $6$,   $7$ . Синус угла между диагоналями $0,2$.     Найти площади треугольников и всего четырехугольника.

• Дано:   $BO=3$     $OD=5$    $CO=6$    $AO=7$ … угол между   $sinangle AOB=0,2$.     Найти:    $S_{ABCD}=?$.
• Решение:       Диагонали делят четырехугольник на 4 треугольника.    Площадь = сумме 4-х площадей.
• Аддитивность:         $S_{ABCD}=S_{bigtriangleup AOB}+S_{bigtriangleup BOC}+S_{bigtriangleup COD}+S_{bigtriangleup AOD}$.        
• Площадь одного из них по формуле:    $S_{bigtriangleup AOB}=frac{1}{2}cdot AOcdot OBcdot sin angle AOB=frac{1}{2}cdot 7 cdot 3cdot 0,2=2,1$
• Каковы синусы остальных углов? Свойство: Синусы смежных углов равны:   $sinangle BOC=sinangle COD=sinangle AOD=0,2$
• Тогда, площади других треугольников   $frac{1}{2}cdot 3 cdot 6cdot 0,2=1,8$         $frac{1}{2}cdot 6 cdot 5cdot 0,2=3$              $frac{1}{2}cdot 5 cdot 7cdot 0,2=3,5$   
• Площадь четырехугольника равна сумме этих площадей    Ответ:     $S_{ABCD}=2,1+1,8+3+3,5=10,4$

Теоретически, по-другому:      Распишем получение площади   $S_{ABCD}$   в буквах, без числовых значений:

• $frac{1}{2}cdot OAcdot OBcdot sin angle AOB+frac{1}{2}cdot OBcdot OCcdot sin angle AOB+frac{1}{2}cdot OCcdot ODcdot sin angle AOB+frac{1}{2}cdot ODcdot OAcdot sin angle AOB$
• Вынос за скобки множителей   $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OAcdot OB+OBcdot OC+OCcdot OD+ODcdot OAright)$
• $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OBcdotleft(OA+OCright)+ODcdotleft(OA+OCright)right)=frac{1}{2}cdot sin angle AOBcdot AC cdot (OB+OD)$
• Получаем   $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$    $Rightarrow$   $S_{ABCD}=frac{1}{2}cdot (7+6) cdot (3+5)cdot 0,2=13cdot 0,8=10,4$

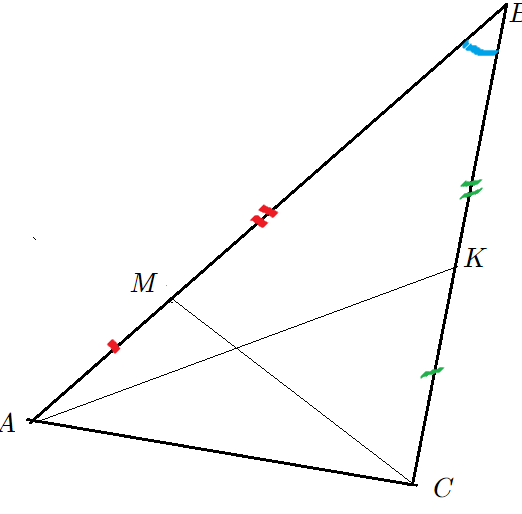
Задача 3:        В треугольнике известны стороны     $AB=10$ ,      $BC=12$ и угол $angle ABC=30$ . Точка $M$ делит сторону $AB$ в отношении 3 : 5, а точка   $K$ делит сторону $BC$ в отношении 2 : 3. Найти площади и отношение площадей треугольников   $ABK$ и   $MBC$.

• Дано:   $AB=10$,     $BC=12$,     $frac{AM}{MB}=frac{3}{5}$,       $frac{BK}{KC}=frac{2}{3}$,     $angle ABC=30$.           Найти:          $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=?$
• Точка делит отрезок в известном соотношении. Находим части как систему уравнений   $frac{x}{y}=?$      $x+y=?$
• $frac{AM}{MB}=frac{3}{5}$,     аддитивность        $AM+MB=AB=10$       $Rightarrow$    $frac{AM}{AB}=frac{3}{3+5}$ $Rightarrow$    $AM=frac{15}{4}$,   $MB=frac{25}{4}$
• $frac{BK}{KC}=frac{2}{3}$,     $BK+KC=12$    из свойств пропорций    $BK=frac{24}{5}$,     $KC=frac{36}{5}$
• Найдем площадь через синус     $S_{bigtriangleup ABK}=frac{1}{2}cdot AB cdot BK cdot sin angle ABC = frac{1}{2}cdot 10 cdot frac{24}{5} cdot sin 30= 24 cdot 0,5=12$
• В треугольнике $MBC$ тот же угол,    $S_{bigtriangleup MBC}=frac{1}{2}cdot MB cdot BC cdot sin angle ABC = frac{1}{2}cdot frac{25}{4} cdot 12 cdot 0,5=frac{75}{4}$         
• отношение площадей треугольников     $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=frac{12}{frac{75}{4}}=frac{16}{25}$                Ответ:         $frac{16}{25}$

Замечание, продолжение:   Можно ли найти отношение площадей при неизвестных значениях сторон и угла?

• Зная лишь как делят точки $M$ и   $K$ стороны треугольника, на какие пропорции ?!
• Дано только   $frac{AM}{MB}=frac{3}{5}$,       $frac{BK}{KC}=frac{2}{3}$.    Выразим отрезки через стороны    $AB$ и     $BC$.
• Выразим площади    $S_{bigtriangleup ABK}$ ,   $S_{bigtriangleup MBC}$ также через стороны $AB$ и     $BC$ и угол $angle ABC$.
• Составим отношение площадей, выразим через стороны и угол. Что получится? Что можно сделать, ?

Теорема “о площади четырехугольника через диагонали и синус угла”:

1. Площадь четырехугольника     равна   половине произведения   диагоналей   на синус угла между ними:
2. Формулы                  $S=frac{1}{2}cdot d_1 cdot d_2 cdotsin angle alpha$                    $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$
3. Площадь   ромба     равна     половине произведения   диагоналей.         … диагонали перпендикулярны!
4. Формулы             $S=frac{1}{2}cdot d_1 cdot d_2=frac{1}{2}cdot AC cdot BD$            $angle AOB=90$          $sin angle AOB=1$

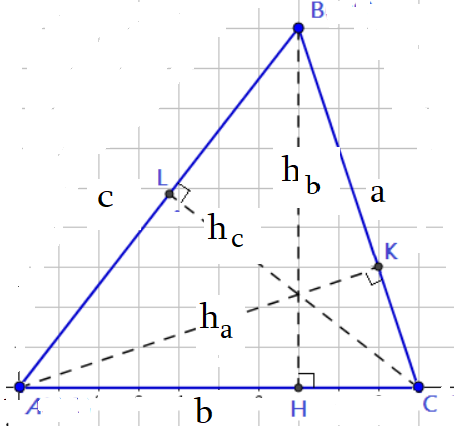
Формулы площади треугольника:   

$S=frac{acdot h_a}{2}=frac{acdot bcdotsin C}{2}$                             $S=frac{bcdot h_b}{2}=frac{bcdot ccdotsin A}{2}$                             $S=frac{ccdot h_c}{2}=frac{ccdot acdotsin B}{2}$.

$sin A=frac{h_b}{c}=frac{h_c}{b}$                            $sin B=frac{h_a}{c}=frac{h_c}{a}$                         $sin C=frac{h_b}{a}=frac{h_a}{b}$.      

$S_{ABC}=frac{1}{2}cdot ACcdot BCcdotsin C$              $S_{ABC}=frac{1}{2}cdot ABcdot BCcdotsin B$                 $S_{ABC}=frac{1}{2}cdot ACcdot ABcdotsin A$ .

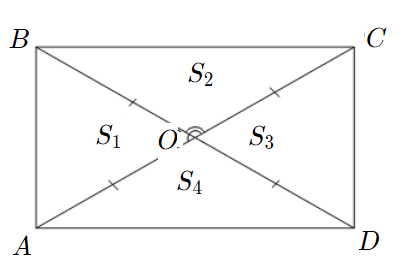
Задача 4:     В прямоугольнике диагонали $10$ и угол между ними $30$. Найти площадь.

• Дано:    $ABCD$    – прямоугольник ,    $AC=10$   ,    $angle AOB=30$   Найти:            $S_{ABCD}$ .
• Решение:       В прямоугольнике диагонали равны и пересекаются по середине    $AO=OB=5$     
• $bigtriangleup AOB$     и     $bigtriangleup COD$     равные    $Rightarrow$     $S_1=S_3$        ;
• $bigtriangleup BOC$     и     $bigtriangleup AOD$     равные    $Rightarrow$     $S_2=S_4$      .
• Смежные, $angle BOC=180-angle AOB=150$. Найдем отношение     $frac{S_1}{S_2}=frac{frac{1}{2}AOcdot OBcdotsin30}{frac{1}{2}BOcdot OCcdotsin150}$
• $sin30=sinleft(180-30right)=sin150$.       тогда      $frac{S_1}{S_2}=frac{frac{1}{2}cdot5cdot5cdotsin150}{frac{1}{2}cdot5cdot5cdotsin150}=1$     Значит,      $S_1=S_2$
• Аналогично:       $frac{S_3}{S_4}=frac{frac{1}{2}DOcdot OCcdotsin30}{frac{1}{2}AOcdot ODcdotsin150} =1$       $Rightarrow$      $S_3=S_4$,     площади равные.
• Диагонали рассекают прямоугольник на   четыре равновеликих: треугольника         $S_1=S_2=S_3=S_4$ .
• … тогда, по свойству аддитивности площадей          $S_1=S_2=S_3=S_4=frac{1}{4}S_{ABCD}$ .
• $S_{AOB}=S_1=frac{1}{2}AOcdot OBcdot sin 30=frac{1}{2}cdot 5cdot 5cdot frac{1}{2}=frac{25}{4}$        $Rightarrow$        $S_{ABCD}=4cdotfrac{25}{4}$
• Найдя площадь АОВ, нашли площадь прямоугольника умножением на 4.   Ответ:        $S_{ABCD}=25$

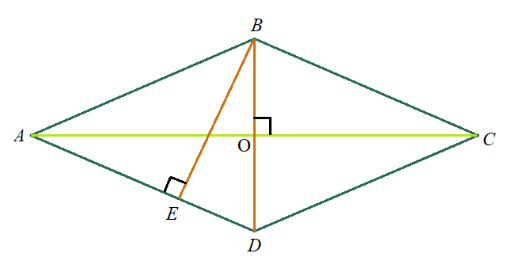
Задача 5:         Найти площадь ромба   $ABCD$,   если его высота   $EB=12$   , а меньшая диагональ $BD=13$.

• Дано:    ромб $ABCD$ , $BD=13$,    высота $EB=12$   ,   Найти:            $S_{ABCD}$ .
• Решение:        прямоугольный $bigtriangleup BED$,    подобен тем, на которые ромб делится диагоналями:        
• $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$    . Одинаковый “состав” углов. Все прямоугольные,
• Прямоугольный    $bigtriangleup BED$,   по Пифагору выразим катет       $DE=sqrt{BD^2-BE^2}=5$
• Диагонали в ромбе делятся пополам:       $BO=OD=frac{BD}{2}=6,5$             $AO=frac{AC}{2}$              $AC=2cdot AO$
• Для нахождения площади ромба нам нужно найти вторую диагональ.
• $bigtriangleup BED sim bigtriangleup AOD$         $Rightarrow$         $frac{AO}{BE}=frac{OD}{ED}$        $Rightarrow$           $AO=frac{ODcdot BE}{ED}=frac{6,5cdot 12}{5}=15,6$         $AC=2cdot AO=31,2$
• Ответ: Площадь ромба через диагонали:     $S_{ABCD}=frac{1}{2}cdot ACcdot BD=0,5cdot 31,2cdot13=202,8$

Задача 6.       Площадь равнобедренного треугольника равна $100$   , а угол при вершине   $30^o$    1) Найти его боковые стороны .     2)   Найти тригонометрию $15^o$   

• Решение:       1)   Известны площадь и угол,   значит используем   формулу   площади через синус   $30^o$ .     
• Пусть боковая   сторона $a$   ,    $S=frac{1}{2}acdot acdotsin30$        ,     тогда    $100=frac{1}{2}a^2cdotsin30$     $Leftrightarrow$     $100=frac{1}{2}a^2cdotfrac{1}{2}$     $Rightarrow$      
• $a=sqrt{400}=20$                     Ответ:       $a=20$
• 2)    По теореме косинусов найдем основание     $c=sqrt{a^2+a^2-2cdot acdot acdotfrac{sqrt{3}}{2}}=asqrt{2-sqrt{3}}$
• Из вершины равнобедренного угла проведем биссектрису к   основанию.   По свойству равнобедренности
• она будет и высотой    $h$   (треугольник поделится на 2 прямоугольных с углами 15 градусов) и медианой,
• а значит основание   поделится пополам ,    как и угол 30 у вершины   поделится   по   15 градусов.
• По прямоугольнему треугольнику   (половинка):      $sin15=frac{0,5cdot c}{a}=frac{0,5cdot acdotsqrt{2-sqrt{3}}}{a}=frac{sqrt{2-sqrt{3}}}{2}$
• Площадь через основание    $S=frac{1}{2}cdot ccdot h$,     найдем высоту      $h=frac{2cdot S}{c}=frac{2cdot0,5cdot a^2cdotsin30}{acdotsqrt{2-sqrt{3}}}=frac{a}{2cdotsqrt{2-sqrt{3}}}$
• В прямоугольном треугольнике стороны $h$,   $frac{c}{2}$,   $a$.   Тогда     $cos15=frac{h}{a}=frac{frac{a}{2cdotsqrt{2-sqrt{3}}}}{a}=frac{1}{2cdotsqrt{2-sqrt{3}}}$

Интерактивные Упражнения

чтобы найти площадь параллелограмма,нужно длину его стороны умножить на длину опущенной на эту сторону высоты.