Как найти площадь параллелограмма — три основных формулы
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья на еще одну математическую тему. Мы расскажем, как правильно посчитать площадь параллелограмма. Эту тему подробно изучают только в 8-м классе. И это говорит, что она не такая простая.

Но для начала давайте все-таки напомним, какая фигура называется параллелограммом.
Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.
Классический параллелограмм выглядит вот так:

Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.
Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.

И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».
Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.
Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.
Формулы для расчета площади параллелограмма
Есть три основных формулы для вычисления площади параллелограмма:
- если известна длина стороны и высота, проведенная к ней;
- если известны длины сторон и углы между ними;
- если известны длины диагоналей и угол между ними.
Теперь о каждом из этих способов подробнее.
Как найти площадь параллелограмма, если известны сторона и высота
Возьмем для примера такой параллелограмм:
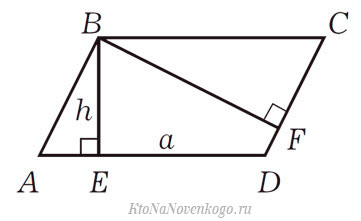
В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.
В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.
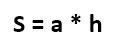
И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.
Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:
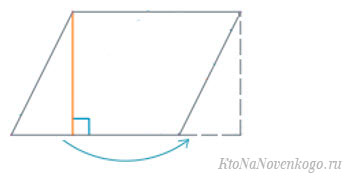
В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.
Формула площади параллелограмма, если известны стороны и угол
Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.
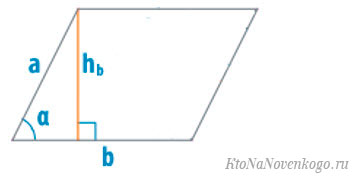
Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.
Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:
![]()
Соответственно, чтобы посчитать значение высоты надо:
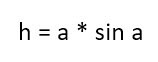
И наша конечная формула для расчета площади будет выглядеть следующим образом:
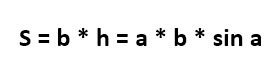
Как найти площадь параллелограмма через диагонали
Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.
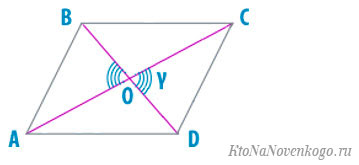
В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:
![]()
Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.
Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.
![]()
Площадь параллелограмма
Простые геометрические расчеты, такие как нахождение площади параллелограмма, можно производить при помощи Яндекса. Наберите в Яндексе:
площадь параллелограмма
Яндекс предложит следующий интерфейс, в который нужно будет подставить значения:

Формула площади параллелограмма
S=ah
где “a” – основание, “h” – высота.
автор вопроса выбрал этот ответ лучшим
![]()
tana76
[124K]
6 лет назад
Площадь параллелограмма – одной из часто встречающихся геометрических фигур – можно искать разными способами, в зависимости от исходных данных или возможности их определить.
Первый способ – через известные стороны и углы параллелограмма.


Второй – через известную сторону параллелограмма и его высоту.


Третий – через диагонали параллелограмма и угол между ними.


![]()
Матвей628
[90K]
9 лет назад
Площадь параллелограмма можно найти, по меньшей мере, тремя способами:
1.Площадь параллелограмма равна произведению основания на высоту, опущенную на это основание

2.Площадь параллелограмма равна произведению двух смежных сторон на синус угла между ними.

3.Площадь параллелограмма равна половине произведения двух диагоналей на синус угла между ними.

![]()
moreljuba
[62.5K]
6 лет назад
Площадь параллелограмма можно найти целыми тремя путями:

1) Во-первых, можно умножить сторону параллелограмм на опущенную к ней высоту;
2) Во-вторых, можно умножить две прилежащие стороны к углу на синус этого угла;
3) В-третьих, можно умножить половину произведений диагоналей параллелограмма на синус угла, располагаемого между диагоналями.
Колючка 555
[61.3K]
7 лет назад
Я знаю 2 способа. Для первого способа необходимо знать длину не параллельных сторон и значение угла между ними.

То есть, в моем случае S=K*T*sinO.
Второй способ. Нужна длина одной стороны и высота от этой стороны, к тупому углу противоположной стороны построенная под прямым углом. S=W*F.

![]()
Annet007
[26.3K]
8 лет назад
Площадь параллелограмма найти не сложно, если знать основную формулу для ее нахождения.
Площадь параллелограмма равна произведению основания на высоту.

Доказательство данной формулы смотрим ниже на скрине:

![]()
sergun
[16.9K]
10 лет назад
чтобы найти площадь параллелограмма,нужно длину его стороны умножить на длину опущенной на эту сторону высоты.
![]()
иришенька
[41.2K]
9 лет назад
Вообще, площадь параллелограмма можно найти 3-мя различными способами(смотря что известно о параллелограмме), например, 1) площадь параллелограмма = основание х на высоту(высоту берём ту, которая опущена на основание).
2) Площадь параллелограмма = 2 смежные стороны умноженные друг на друга и умноженные на синус угла, который они составляют.
3) Площадь параллелограмма = одна диагональ х на другую диагональ/2 х на синус угла, который они составляют(берём меньший угол).
По-моему, будет так.
![]()
galvanna
[52.7K]
9 лет назад
Какой хороший школьный вопрос! Я очень соскучилась по параллелограмму.)

Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны.
Для того, чтобы найти площадь параллелограмма необходимо сторону параллелограмма умножить на высоту проведённую к этой стороне. То есть S = AD*BE
или S= AB*AD*sin<BAD – произведение смежных сторон на синус угла между ними,
а так же половина произведения диагоналей параллелограмма на синус угла между ними 1/2AC*BD*sin<AOB.
Есть несколько формул для расчета площади параллелограмма:
- Умножить основание на высоту: S = a*h
- Умножить две смежные стороны на синус угла между ними: S = a*b*sinα
- Произведение диагоналей на синус угла между ними и всё это поделить на два: S = (1/2)*d1*d2*sinα
Или рассчитать онлайн на сайте http://100formul.ru/44
Для того,чтобы вычислить площадь параллелограмма,нужно узнать величины основания и высоты,опущенной к этому основанию, затем перемножить данные числа.Это и будет являться площадью параллелограмма.
Это самый легкий способ,по сравнению с другими.
Знаете ответ?

{S = a cdot h}
Найти площадь параллелограмма
На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные – основание, высоту, стороны, диагонали и углы между ними и получите ответ.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Содержание:
- калькулятор площади параллелограмма
- формула площади параллелограмма через сторону и высоту
- формула площади параллелограмма через две стороны и угол между ними
- формула площади параллелограмма через диагонали и угол между ними
- примеры задач
Формула площади параллелограмма через сторону и высоту
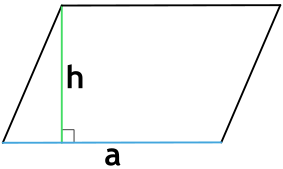
{S = a cdot h}
a – сторона параллелограмма
h – высота параллелограмма
Формула площади параллелограмма через две стороны и угол между ними

{S=a cdot b cdot sin(alpha)}
a, b – стороны параллелограмма
α – угол между сторонами a и b
Формула площади параллелограмма через диагонали и угол между ними
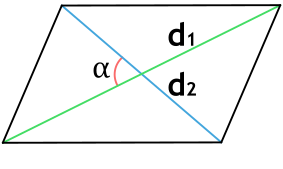
{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}
d1, d2 – диагонали параллелограмма
α – угол между диагоналями
Примеры задач на нахождение площади параллелограмма
Задача 1
Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.
Решение
Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.
S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Мы можем проверить ответ с помощью калькулятора .
Задача 2
Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.
Решение
Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.
S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2
Ответ: 48 см²
И снова проверить ответ нам поможет калькулятор .
Задача 3
Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.
Решение
В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.
S = a cdot h = 12 cdot 8 = 96 : см^2
Ответ: 96 см²
И снова проверить ответ нам поможет калькулятор .
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
![]()
0
Как найти площадь параллелограмма, если неизвестна высота?
1 ответ:
![]()
0
0
Площадь параллелограмма находится через произведение длины основания a на высоту h. S = a * h.
Если это школьная задачка, в которой высота не известна, то должен быть известен какой-то другой параметр, через который можно вычислить высоту.
Если будет более конкретный вопрос, то тогда можно будет дать более конкретный ответ.
Читайте также
![]()
Площадь трапеции S=h*(a+b)/2, где h – высота трапеции, a и b – большое и малое основание трапеции. Из этого уравнения имеем a+b=2*S/h. По условию задачи a=b+6, тогда 2b+6=240/8=30, 2b=24, b=12 см, а=18 см. Боковую наклонную сторону трапеции d находим по теореме Пифагора d =√(h^2+(a-b)^2)=√(64+36)=10 см.
![]()
Нужно перемножить его диагонали и разделить произведение пополам. Чтобы не зубрить и не путать, можно объяснить как-нибудь этот процесс для себя. Лично я в школе прибегал к такой уловке. Диагонали делят ромб на 4 прямоугольных треугольника. Добавляя еще четыре таких же, мы получим прямоугольник, в который вписан этот ромб. Его площадь равна произведению сторон, которые равны диагоналям ромба. При этом площадь самого прямоугольника в 2 раза больше площади ромба. Поэтому площадь ромба равна половине площади прямоугольника, в который он вписан. Это долго объяснять словами, но картинка говорит сама за себя.

![]()
При перемещении круга вдоль одной из сторон правильного шестиугольника, наиболее удалённые от стороны шестиугольника точки круга начертят прямые, параллельные стороне шестиугольника. В итоге получится прямоугольник 4х8 см, к большим сторонам которого примкнуты полукруги. Так произойдёт при перемещении круга по каждой стороне шестиугольника. Внутренние части получившихся фигур перекрывают друг друга и площадь шестиугольника. Поскольку в задаче не требуется учесть перекрывание, то нам достаточно знать, что исходный шестиугольник полностью входит в результирующую фигуру. Его площадь 6*4*4*√(3)/4=24*√(3) см^2.
На каждой стороне шестиугольника с наружной стороны получились квадраты со стороной 4 см. Площадь каждого 4*4=16 см^2, а всех вместе 6*16=96 см^2. В оставшихся между квадратами промежутках получатся секторы кругов, всего 6 секторов, каждый по 1/6 части полного круга (по 60°). Площадь каждого из секторов равна Пи*4*4/6, а всех вместе 16*Пи см^2. Осталось всё сложить: Искомая площадь равна (24*√(3)+96+16*Пи) см^2.
![]()
Площадь прямоугольной трапеции найти очень просто: достаточно вспомнить, из что представляет собой эта геометрическая фигура. Трапеция состоит из двух параллельных и двух боковых сторон, причем одна из боковых сторон имеет угол в 90 градусов.
Найти площадь трапеции можно по следующим формулам:
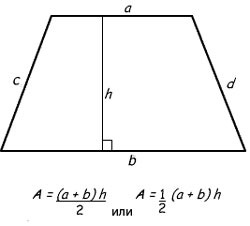
![]()
Сторона АВ=√16=4
Сторона АС=√12-
Значения 4 и √12 получаются как стороны соответствующих квадратов.
Рассмотрим ∆ АВС.
В нем АВ- гипотенуза,а АС-один катет,и СВ- другой катет,тогда
СВ^2=16-12=4.
Ответ S СВNT=4
1. Формула площади параллелограмма через стороны и углы

a, b – стороны параллелограмма
α, β – углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):

Калькулятор – вычислить, найти площадь параллелограмма:
a(сторона)=
b(сторона)=
α или β (угол в градусах)= ( sin α=sin β )
S=
2. Формула площади параллелограмма через сторону и высоту

a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D – большая диагональ
d –меньшая диагональ
α, β – углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):

Калькулятор – вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
