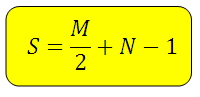Рассмотрим несколько задач на данную тему.
| #1 | #2 | #3 | #4 | #5 |
Задача #1
(Номер задачи на fipi.ru — 71E23E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Прежде чем приступать к решению задачи, вспомним теорию >>
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Площадь параллелограмма вычисляется по формуле:
где a — основание параллелограмма, h — высота параллелограмма.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 7, а высота: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 28 ед. кв.
Задача #2
(Номер задачи на fipi.ru — 3BD9B6). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 15 ед. кв.
Задача #3
(Номер задачи на fipi.ru — 5C5046). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 20 ед. кв.
Задача #4
(Номер задачи на fipi.ru — 566A4E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 18 ед. кв.
Задача #5
(Номер задачи на fipi.ru — 0275CC). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 6.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 36 ед. кв.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
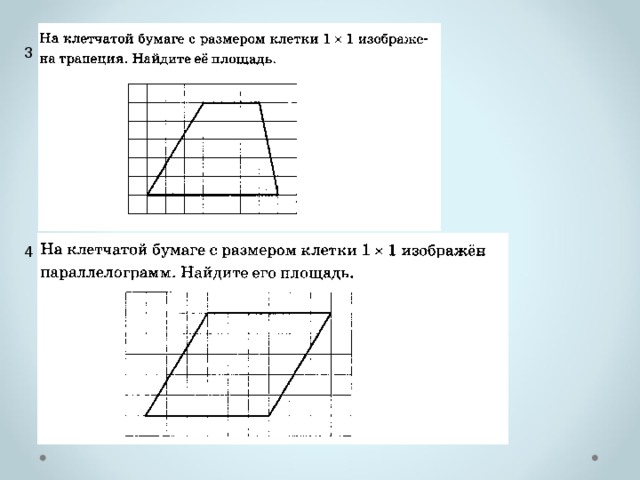
1
На рисунке изображен параллелограмм ABCD. Используя рисунок, найдите
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)
2
На рисунке с размером клетки 1×1 изображен параллелограмм ABCD. Используя рисунок, найдите
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.5)
3
На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
4
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
5
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
Пройти тестирование по этим заданиям
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
Смотри также материал: Как быстро выучить формулы
В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.
Средняя линия трапеции равна полусумме её оснований:
Ответ: 3.
2. Найдите величину угла ABC. Ответ дайте в градусах.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна
Тогда
Ответ: 45.
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на
Решение:
Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:
Осталось умножить найденное значение синуса на
Ответ: 1.
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:
, где
и
— диагонали.
Получим:
Ответ: 12.
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции
Ответ: 18.
Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны
и
. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
.
Ответ: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
.
Ответ: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.
Посмотрим, как решается задача 7 с помощью формулы Пика:
Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
Решение:
На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.
Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 – 4 = 32.
Ответ: 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна
.
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как
. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна
(так как
), а длина дуги данного сектора равна
, следовательно, длина дуги в
раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в
раз меньше, чем полный круг (то есть
градусов). Значит, и площадь сектора будет в
раз меньше, чем площадь всего круга.
Ответ: .
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.
На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть
круга.
Значит, нам надо умножить площадь круга на . Получим:
Ответ: 1,05.
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.
Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в
раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.
Ответ: 7.
Задачи на координатной плоскости
13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).
Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
Ответ: 20
14. Найдите площадь четырехугольника, вершины которого имеют координаты
На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
Ответ: 16.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Решение задач на нахождение площади геометрических фигур на сетке.
ОГЭ . Задание № 19
Подготовила учитель математики МОУ Школа с.Харсаим Филиппова Р.Р.
Характеристика задания
Задание 19 ОГЭ по математике представляет собой задачу по планиметрии на вычисление по готовому чертежу, изображённому на клетчатой бумаге. В таких задачах данные представлены в виде чертежа на бумаге в клетку, причём размеры клеток одинаковы и заданы условием. Это задачи на вычисление углов, расстояний, площадей, связанные со всеми изучаемыми в школьном курсе фигурами. Клетки в таких задачах по сути выполняют роль линейки: посчитав «по клеточкам» необходимые длины и используя известные геометрические факты и свойства, можно довольно быстро получить ответ на вопрос задачи.
Определение
- Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник
Единицы измерения площади
За единицу измерения площадей принимают квадрат со стороной 1см.
- Квадратный метр , производная единица Международной системы единиц (СИ) ; 1 м² = 1 са ( сантиар );
- Квадратный километр , 1 км² = 1 000 000 м²;
- Гектар, 1 га = 10 000 м²;
- Ар (сотка), 1 а = 100 м²:
- Квадратный дециметр, 100 дм² = 1 м²;
- Квадратный сантиметр, 10 000 см² = 1 м²;
- Квадратный миллиметр, 1 000 000 мм² = 1 м²;
Свойства площади
- Фигуры имеющие равные площади называются равновеликими.
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата равна квадрату его стороны.
Основные формулы для нахождения площади.
Площади треугольников
S = ½*a*h S = ½*a*b sinα S = r*p
S =
S = – формула Герона
(p = – полупериметр)
S = π*R 2 площадь круга
Основные формулы для нахождения площади.
Площади четырехугольников
Прямоугольник
S=a*b S= ½* d 2 sinφ
а и в – стороны прямоугольника
d – диагональ прямоугольника
φ- угол между диагоналями
Квадрат
S = a 2 S =1/2* d 2
а – сторона квадрата
d – диагональ квадрата
Параллелограмм
S=a*h S=a*b*sinα
S= ½* d 1 *d 2 sinφ
Ромб
S=a*h S=a 2 sinα
S= ½* d 1 *d 2
Трапеция
S = S = ½* d 1 * d 2 sinφ
а и в – основания трапеции; -длина средней линии ; d 1 и d 2 -диагонали трапеции; sinφ -угол между диагоналями
Одним из основных заданий Модуля Геометрия являются задачи на нахождение площади фигур на сетке. Многие ученики сводят решение этого задания к подсчету клеток внутри фигуры. Такой способ не всегда дает точный результат. Поэтому я предлагаю рассмотреть основные способы решения таких задач.
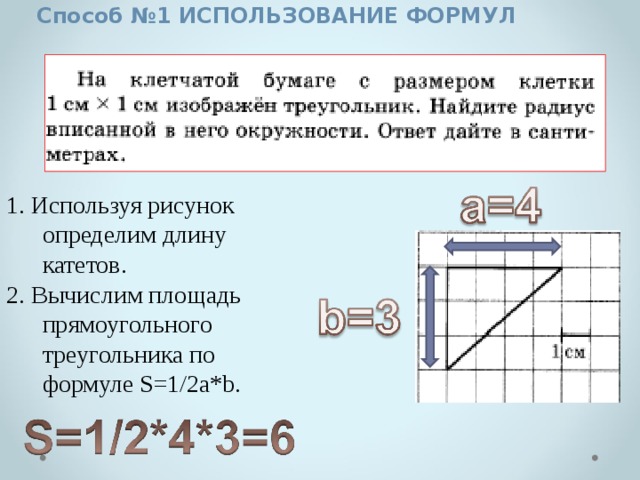
Способ №1 ИСПОЛЬЗОВАНИЕ ФОРМУЛ
1. Используя рисунок определим длину катетов.
2. Вычислим площадь прямоугольного треугольника по формуле S=1/2a*b.
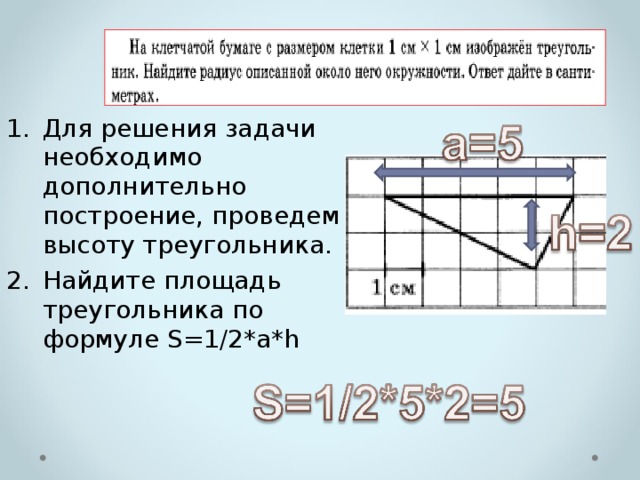
- Для решения задачи необходимо дополнительно построение, проведем высоту треугольника.
- Найдите площадь треугольника по формуле S=1/2*а*h
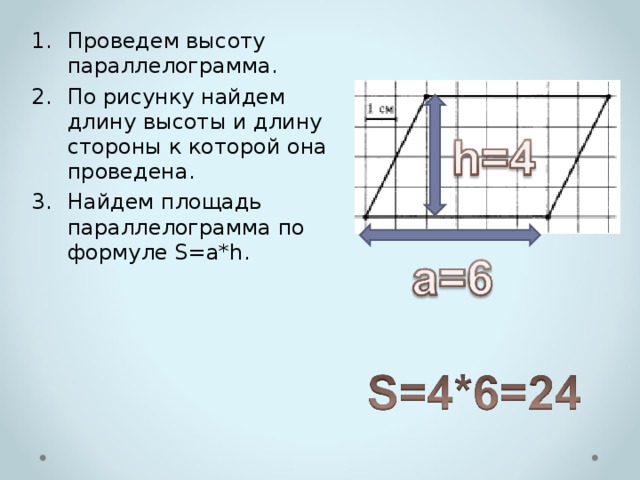
- Проведем высоту параллелограмма.
- По рисунку найдем длину высоты и длину стороны к которой она проведена.
- Найдем площадь параллелограмма по формуле S=a*h.
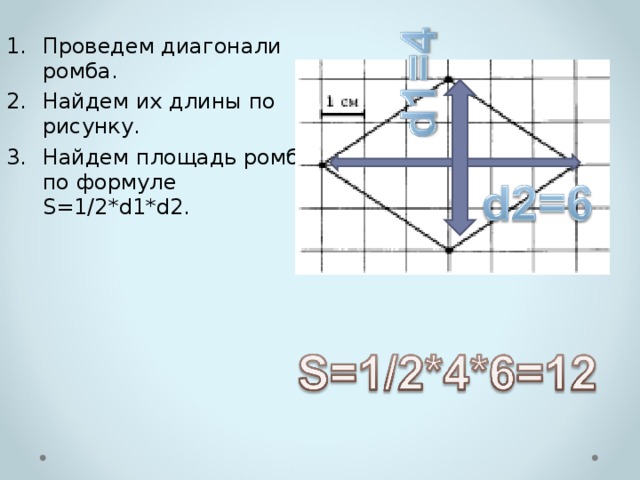
- Проведем диагонали ромба.
- Найдем их длины по рисунку.
- Найдем площадь ромба по формуле S=1/2*d1*d2.
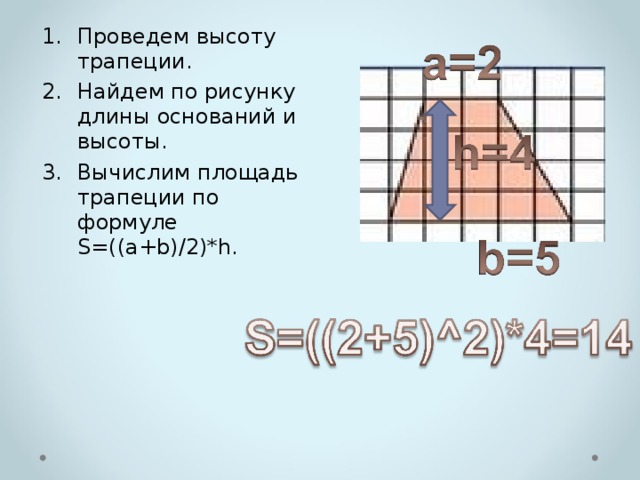
- Проведем высоту трапеции.
- Найдем по рисунку длины оснований и высоты.
- Вычислим площадь трапеции по формуле S=((a+b)/2)*h.
Способ №2 Разделение фигуры на прямоугольные треугольники, прямоугольники, квадраты.
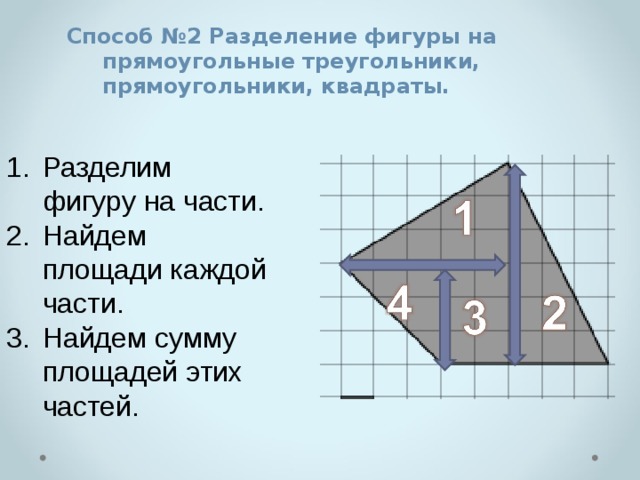
- Разделим фигуру на части.
- Найдем площади каждой части.
- Найдем сумму площадей этих частей.
- Фигуры 1,4,2 –прямоугольные треугольники. Их площади найдем по формуле S=1/2*a*b.
- Фигура 3-прямоугольник. Его площадь легко найти даже подсчетам клеток. Его площадь равна 6.
- Сложив площади треугольников и прямоугольника мы найдем площадь искомой фигуры.
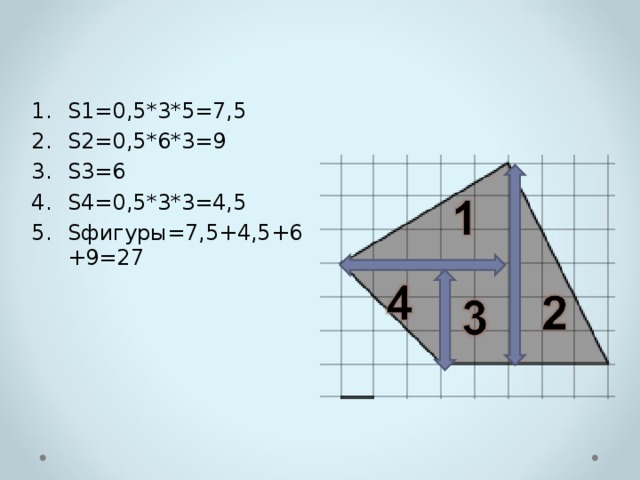
- S1=0,5*3*5=7,5
- S2=0,5*6*3=9
- S3=6
- S4=0,5*3*3=4,5
- Sфигуры=7,5+4,5+6+9=27
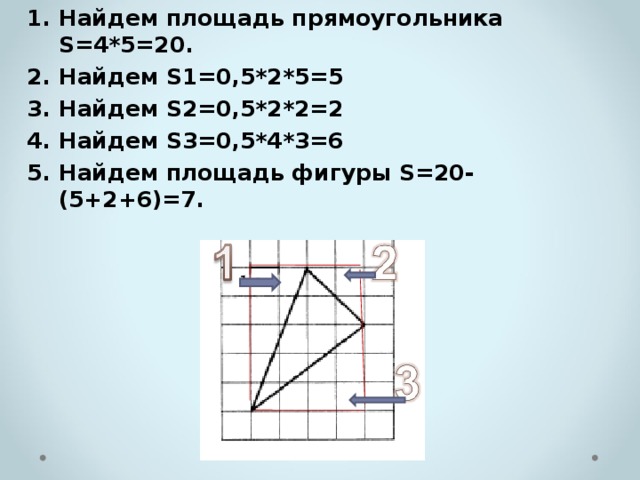
Способ №3
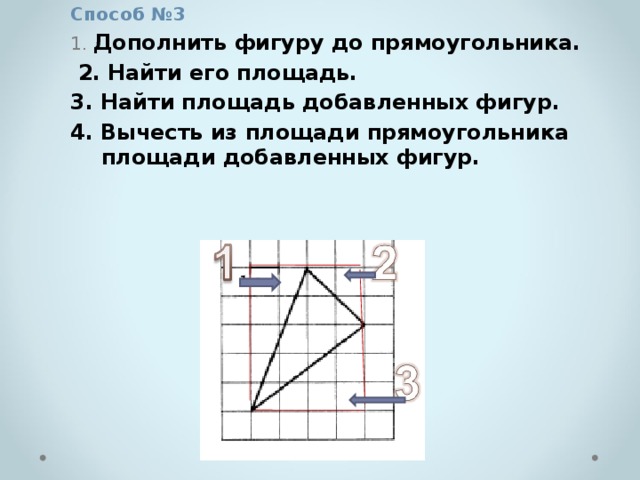
1. Дополнить фигуру до прямоугольника.
2. Найти его площадь.
3. Найти площадь добавленных фигур.
4. Вычесть из площади прямоугольника площади добавленных фигур.
- Найдем площадь прямоугольника S=4*5=20.
- Найдем S1=0,5*2*5=5
- Найдем S2=0,5*2*2=2
- Найдем S3=0,5*4*3=6
- Найдем площадь фигуры S=20-(5+2+6)=7.
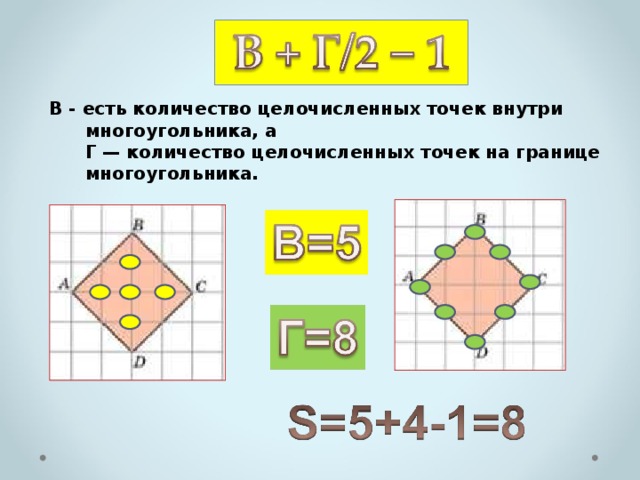
Способ №4 Формула Пика.
Площадь многоугольника с целочисленными вершинами равна В + Г/2 − 1 , где В – есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
В – есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
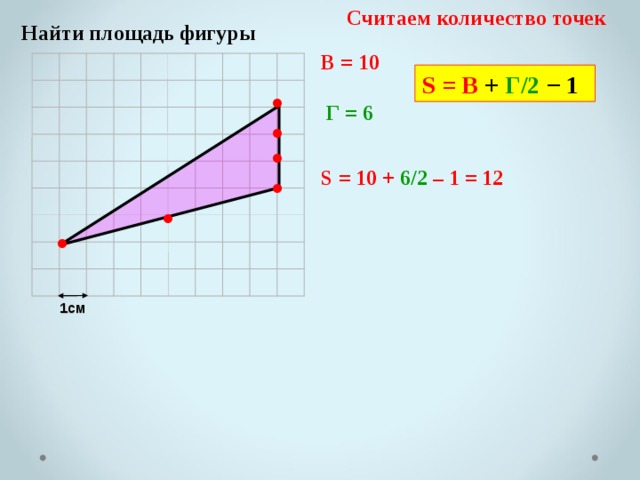
Считаем количество точек
Найти площадь фигуры
В = 10
S = В + Г/2 − 1
●
Г = 6
●
●
S = 10 + 6/2 – 1 = 12
●
●
●
1см
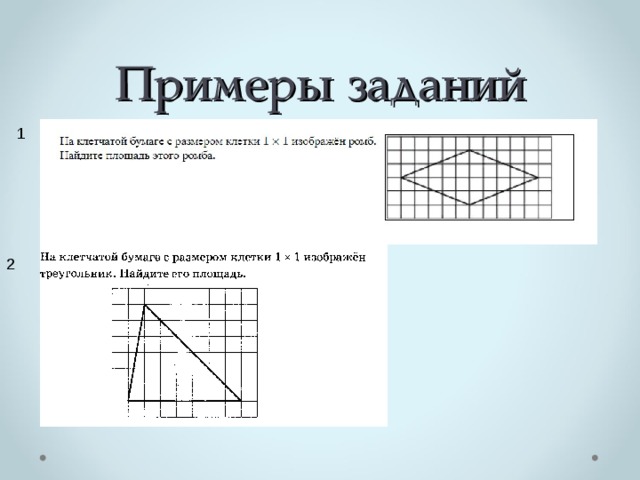
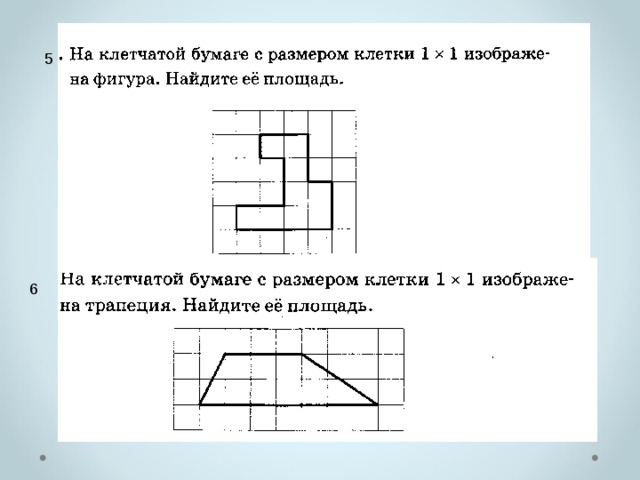
Примеры заданий
1
2
3
4
5
6
Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.
Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.
В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.
ФОРМУЛА ПИКА
Площадь искомой фигуры можно найти по формуле:
М – количество узлов на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника
*Под «узлами» имеется ввиду пересечение линий.
Найдём площадь треугольника:
Отметим узлы:
1 клетка = 1 см
M = 15 (обозначены красным)
N = 34 (обозначены синим)
Ещё пример. Найдём площадь параллелограмма:
Отметим узлы:
M = 18 (обозначены красным)
N = 20 (обозначены синим)
Найдём площадь трапеции:
Отметим узлы:
M = 24 (обозначены красным)
N = 25 (обозначены синим)
Найдём площадь многоугольника:
Отметим узлы:
M = 14 (обозначены красным)
N = 43 (обозначены синим)
Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.
А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.
Теперь взгляните на следующие фигуры:
Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:
Отметим узлы:
M = 11 (обозначены красным)
N = 5 (обозначены синим)
Ответ: 9,5
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.
Рассмотрим подход оговоренный в статье “Площадь четырёхугольника. Универсальный способ“.
Найдём площадь фигуры:
Опишем около неё прямоугольник:
Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:
Ответ: 4,5
В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.