Содержание:
- Формулы
- Примеры вычисления площади параллелограмма
Формулы
Первый способ. Чтобы найти площадь параллелограмма (рис. 1), нужно найти произведение стороны
$a$ параллелограмма на высоту
$h_a$, проведенную к этой стороне, то есть

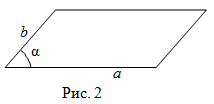
Второй способ. Чтобы найти площадь параллелограмма, надо найти произведение двух его смежных сторон
$a$ и $b$, умноженное на синус угла
$alpha$ между ними (рис. 2):
$$mathrm{S}=a b sin alpha$$
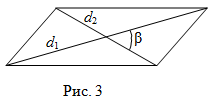
Третий способ. Чтобы найти площадь параллелограмма, надо найти полупроизведение его диагоналей
$d_1$ и $d_2$ на синус угла $beta$ между ними (рис. 3):
$$mathrm{S}=frac{1}{2} d_{1} d_{2} sin beta$$
Примеры вычисления площади параллелограмма
Пример
Задание. Найти площадь параллелограмма, если его сторона равна 2 см, а высота, проведенная к этой стороне – 3 см.
Решение. Искомая площадь равна
$S=2 cdot 3 = 6$ (см2)
Ответ. $S=6$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти площадь параллелограмма, одна сторона которого равна 4 см, вторая на 3 см
больше и тупой угол параллелограмма равен $120^{circ}$.
Решение. Найдем вторую сторону параллелограмма:
$b=4+3=7$ (см)
Так как сумма углов параллелограмма, прилежащих к одной стороне, равна
$180^{circ}$, то делаем вывод, что угол между сторонами равен
$$alpha=180^{circ}-120^{circ}=60^{circ}$$
Тогда искомая площадь равна
$mathrm{S}=4 cdot 7 cdot sin 60^{circ}=28 cdot frac{sqrt{3}}{2}=14 sqrt{3}$ (см2)
Ответ. $mathrm{S}=14 sqrt{3}$ (см2)
Остались вопросы?
Здесь вы найдете ответы.
Каким образом можно доказать утверждение о том, что площадь параллелограмма
есть число, получаемое в результате умножения длин двух его сторон,
являющихся смежными, и синуса угла, который образуется между ними?
Параллелограмм следует расположить по горизонтали. Обозначим его верхнее
основание как АВ, а противоположное ему основание – как CD. Из точек ВЕ и
AF проведем перпендикулярные прямые на нижнее основание фигуры. В
результате получится прямоугольник ABEF. Площадь образовавшейся
прямоугольной фигуры равна площади параллелограмма по той причине, что
параллелограмм ABCD и фигура с прямыми углами ABEF являются
равносоставленными, о чем свидетельствует равенство треугольников ВEC и
DAF.
Площадь (S) прямоугольника представляет собой произведение длин сторон EF
и FA, которое, в свою очередь, равно:
CD*AD*sin(CDA)
Именно это и требовалось доказать.
Параллелограмм имеет смежные стороны длиной 26 см и 32 см. Один из углов
данной фигуры равен 150 градусам. Каким способом можно вычислить площадь
параллелограмма?
Обозначим имеющийся параллелограмм как АВСD. Тогда одна его сторона АВ
равна 26 см, а другая АD – 32 см. Угол АВС параллелограмма составляет 150
градусов.
Принимая во внимание тот факт, что сумма внутренних односторонних углов
параллелограмма равна 180 градусов, можно говорить о том, что его угол ВАD
составляет 30 градусов. Проведем высоту ВК, и в итоге получим треугольник
АВК с прямым углом. Длина опущенной высоты как катета, расположенного
противоположно углу в 30 градусов, равна 13 см. Площадь (S)
параллелограмма есть число, полученное в результате умножения длины высоты
на длину стороны. Это значит, что:
S (АВСD) = 13 *32 = 416 см кв.
Ответ: Площадь параллелограмма равна 416 см кв.
Прямая АС проведена через середины двух сторон параллелограмма, которые
являются смежными. Данная прямая отсекает от параллелограмма два
треугольника – FMD и АDС. Площадь одного из отсеченных треугольников
составляет 32 см кв. Как высчитать площадь параллелограмма?
Прямая АС представляет собой диагональ биссектрисы. В этом случае
образовавшиеся посредством ее проведения треугольники FMD и АDС являются
подобными по причине наличия общего угла А и равенства сторон. На
основании этого можно говорить о том, что:
SADC=1/2*ab*sin a
SFDM=1/2 *2a*2b sin a
SADC / SFDM= 32/x
1/4=32/x
x=128
Теперь можно рассчитать площадь параллелограмма (S), которая будет равна
2*х:
S = 128*2 = 256 см кв.
Ответ: Площадь параллелограмма равна 256 см кв.
Параллелограмм имеет стороны, длины которых составляют 10 см и 6 см. Данные
стороны образуют угол, равный 150 градусам. Как рассчитать площадь
параллелограмма в этом случае?
Обозначим угол в 150 градусов буквой В. Зная о том, что внутренние
односторонние углы параллелограмма в сумме дают 180 градусов, можно
вычислить второй угол А. Он будет равен:
∠А = 180-150 = 30 градусов.
Теперь следует провести высоту ВВ1, которая образует треугольник АВВ1,
являющийся прямоугольным. Длина ВВ1 будет равна половине длины стороны,
равной 6 см:
ВВ1 = 6/2 = 3 см.
Тогда площадь (S) параллелограмма можно рассчитать, умножив длину ВВ1 на
10 см (длина смежной стороны):
S = 3*10 = 30 см кв.
Ответ: Площадь параллелограмма равна 30 см кв.
Проведенные диагонали делят параллелограмм на четыре треугольных фигуры.
Площадь одной из них равна 7 м кв. Каким образом можно найти площадь
параллелограмма?
Обозначим имеющийся параллелограмм как ABCD. Точкой пересечения его
диагоналей является точка О. Образованные диагоналями треугольные фигуры
ABO, BCO, CDO, DAO являются одинаковыми по площади. Об этом
свидетельствует тот факт, что диагонали параллелограмма делятся ровно
пополам в точке их пересечения. Свидетельством того, что все четыре
треугольника имеют одинаковые площади, выступает равенство синусов смежных
углов. Площадь является ½ числа, которое получено в результате умножения
длин сторон треугольника и синуса угла, образованного между ними.
Параметры, которые отвечают вычислению площадей треугольников, равны, а
это означает равенство и самих площадей.
Если площади всех четырех треугольных фигур равны, то площадь самого
параллелограмма будет в четыре раза превышать площадь любого из них. Это
значит, что площадь (S) параллелограмма может быть вычислена следующим
образом:
S = 4*7 = 28 м кв.
Ответ: Площадь параллелограмма равна 28 м кв.
Дан параллелограмм ABCD, на одной из сторон которого АВ поставлена точка М.
Известно, что площадь треугольника MCD составляет 38 см кв. Как найти
площадь параллелограмма?
Площадь (S) параллелограмма рассчитывается путем умножения длины его
основания на длину его высоты.
Прямые МС и МD, проведенные из точки М, делят параллелограмм на
треугольники. Площадь первого из них вычисляется как:
S₁ = 1/2 * a * h = 38 см кв.
Формула для расчета площади второго треугольника выглядит так:
S₂ = 1/2 * a₁* h
Площадь третьего треугольника можно найти следующим образом:
S₃ = 1/2 *a₃* h,
где а =а₁ + а₂
Теперь через площади образованных треугольников можно вычислить площадь
параллелограмма:
S = S₁ + S₂ + S₃ = 1/2 *(a * h +a₁ * h +a₂ * h) = 1/2 * (a * h + h(a₁ +
a₂)) = 1/2 * (a * h + a * h) = 2 * 38 = 76 см. кв.
Ответ: Площадь параллелограмма равна 76 см кв.
Длина основания параллелограмма составляет 5 см, а его высота равна 3 см.
Как найти площадь параллелограмма?
Формула расчета площади параллелограмма (S) включает длину его высоты и
длину его основания. Данные элементы нужно перемножить, для того чтобы
вычислить площадь фигуры:
S = a*h= 5*6=30 см кв.
Ответ: Параллелограмм имеет площадь 30 см кв.
Имеется параллелограмм ABCD. Посередине его стороны АВ поставлена точка Е,
из которой проведена прямая, образующая треугольник CDE площадью 36 см кв.
Каким образом можно найти площадь параллелограмма?
На продолжение стороны CD опустим перпендикуляр ЕН из точки Е. Он
представляет собой высоту для параллелограмма ABCD и треугольника CDE.
Известно, что площадь (S) параллелограмма является произведением длины его
стороны и высоты, которая на нее опущена. Площадь треугольника
представляет собой ½ от числа, которое получилось в результате умножения
длины стороны на высоту, опущенную на нее. На основании этого можно
сделать вывод о том, что:
S(ABCD) = EH*CD
S(∆CDE) = ½*EH*CD => 2*S(∆CDE) = EH*CD.
Из этого следует, что:
2*S(∆CDE) = S(ABCD) = 2*36 ед² = 72 ед. кв.
Ответ: Площадь параллелограмма составляет 72 кв. ед.
В каком виде представлена формула, которая предназначена для вычисления
площади параллелограмма?
Для получения возможности рассчитать, чему равна площадь (S)
параллелограмма, нужно располагать сведениями о длине его основания (а) и
высоты (h). В этом случае площадь можно высчитать при помощи следующей
формулы:
S = а* h.
Как найти площадь параллелограмма через синус, если известно, что длины его
сторон равны 8 см и 10 см, а синус одного из его углов составляет 0,05?
Формула, которая предназначена для вычисления площади параллелограмма (S)
через синус, выглядит следующим образом:
S = a × b × sin A
В данной формуле буквами a и b обозначены стороны параллелограмма,
являющиеся смежными, а А означает угол, который образован между этими
сторонами.
Доказано, что синусы смежных углов являются равными. Это значит, что синус
тупого угла равен синусу острого угла.
Площадь параллелограмма вычисляем следующим образом:
S = 8 × 10 × 0,05 = 4 см кв.
Ответ: Параллелограмм имеет площадь, равную 4 см кв.
Имеется параллелограмм ABCD, в котором опущена высота на его сторону АВ. Ее
длина равна 12 см. При этом длина AD составляет 24 см. Каким образом можно
высчитать значение синуса угла А?
Высота, опущенная на сторону АВ параллелограмма, обозначена как СК.
Полученный в результате треугольник КВС имеет прямой угол.
Sin B=АВ/ВС.
В этом случае ВС=AD=24 см. Так, синус угла В равен:
sinВ=12/24=1/2, что соответствует углу 30 градусов.
В параллелограмме проведены диагонали, длины которых равны 5 см и 28 см.
Между ними образован угол, составляющий 30 градусов. Как можно найти площадь
параллелограмма через синус в данном случае?
Площадь любой из четырехугольных фигур может быть вычислена, если известны
длины ее диагоналей и синус угла, образованного между ними. Для этого
нужно произвести умножение упомянутых величин, а затем разделить
полученное число на 2. В случае с параллелограммом, обозначенным как ABCD,
площадь рассчитывается по этой же формуле:
S = 1/2 AC*BD*sin∠AOB = ½*28*5*sin30° = 14*5*1/2 = 7*5 = 35 кв. см.
Ответ: Площадь параллелограмма равна 35 см кв.
Представляется ли возможным высчитать площадь параллелограмма при условии,
что длины двух его диагоналей и образованный в месте их пересечения угол
являются известными величинами?
Площадь параллелограмма (S) представляет собой половину числа, полученного
после умножения друг на друга длин проведенных в нем диагоналей, которое
умножено на синус образовавшегося в итоге их пересечения угла:
S = ½*d 1*d 2*sin α
Возможно ли рассчитать площадь параллелограмма по диагоналям, длины которых
равны 6 см и 4 см? При этом известно, что образованный ими угол является
прямым.
Для определения площади параллелограмма через известные длины проведенных
в нем диагоналей применяется приведенная ниже формула:
S = ½*d 1*d 2*sin α,
где диагонали фигуры обозначены как d 1 и d 2, а синус образованного в
результате их пересечения угла – sin α.
Подставим в указанное равенство величины, приведенные в задании:
S = 1/2 * 4 см * 6 см * sin 90° = 12 см кв.
Ответ: Площадь параллелограмма, вычисленная через диагонали, равна 12 см
кв.
На одной из сторон параллелограмма ABCD, обозначенной как ВС, отмечена точка
М. Чему будет равна площадь параллелограмма при условии, что площадь
треугольника МАD составляет 21 см кв.?
Под площадью параллелограмма (S) понимается величина, полученная в
результате умножения длины его стороны (b) на высоту (h), которая опущена
к ней. В виде формулы это выглядит следующим образом:
S =b*h
Площадь треугольной фигуры представляет собой ½ числа, полученного
произведением длины стороны на высоту, которая к ней проведена:
S=1/2*b*h,
Отсюда получаем, что:
b*h=2Sт=2*21=42 см кв.
Если говорить о треугольнике МАD, то в нем сторона АD представлена в
качестве стороны b, как и в случае с параллелограммом. Высота указанного
треугольника будет также представлять собой высоту параллелограмма. Это
обусловлено тем, что точка М расположена на стороне, которая
противоположна стороне ВС. Из этого следует, что площадь параллелограмма
равна 42 см кв.
Ответ: Площадь параллелограмма равна 42 см кв.
Параллелограмм ABCD имеет стороны длиной 10 см и 14 см, а также острый угол
в 60 градусов. Каким образом можно вычислить площадь параллелограмма?
В параллелограмме ABCD нужно провести высоту ВН на сторону AD. После этого
получается треугольник АВН с углом в 90 градусов. Можно рассчитать, чему
равен еще один угол данного треугольника:
АВН = 90-60 = 30
ВН = АВ*sin60 = 10*корень3/2 = 5*корень3
Таким образом, можно узнать, чему будет равна площадь параллелограмма:
S = AD*ВН = 14*5*√3 = 70*√3 см кв.
Ответ: Площадь параллелограмма составляет 70*√3 см кв.
Дан параллелограмм, через середины пары смежных сторон которого проведена
прямая. Она отсекает треугольную фигуру площадью 32 см кв. Чему в данном
случае равна площадь параллелограмма?
АС представляет собой диагональ биссектрисы. В этом случае оба
треугольника FMD и ADC являются подобными по той причине, что они имеют
общий угол А и их стороны равны. Из этого следует, что:
S ADC = 1/2*ab*sina
S FDM=1/2 *2a*2bsina
Отношение площадей двух треугольников выглядит как:
S ADC / S FDM= 32/x
1/4=32/x
x=128
Теперь можно высчитать площадь параллелограмма:
S = 128*2 = 256 см кв.
Читать дальше: как найти площадь трапеции.
Учебник
Геометрия, 9 класс
Формулы площадей через синус угла
Основные свойства площадей фигур:
- Равные фигуры имеют равные площади. Две фигуры состоящие из одинаковых кусков – равновеликие.
- Аддитивность: Площадь фигуры, разрезанной на несколько частей, равна сумме площадей этих частей ;
- Площадь прямоугольника равна произведению ширины на длину … произведение сторон.
Задача 1: В параллелограмме известны стороны $7$, $10$ и синус угла между ними $frac{1}{2}$. Найти площадь параллелограмма.
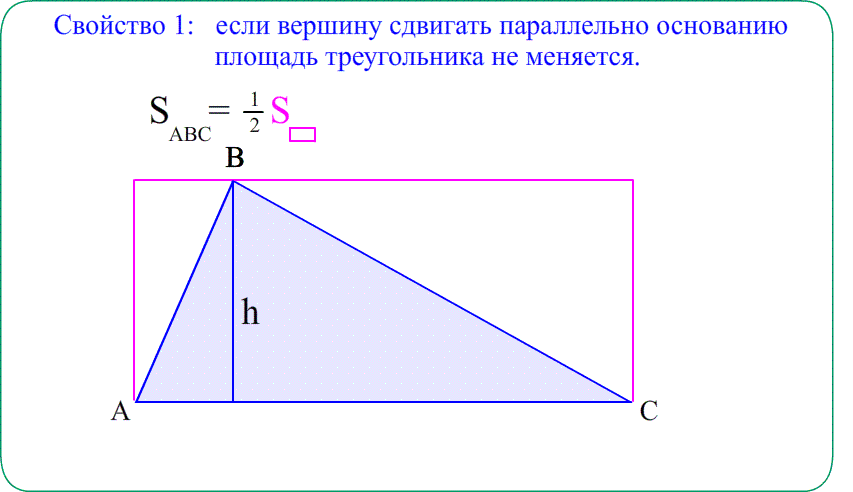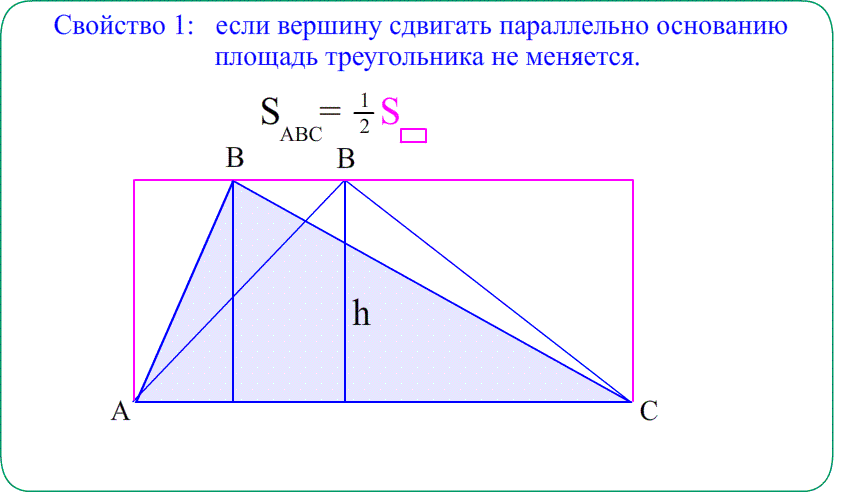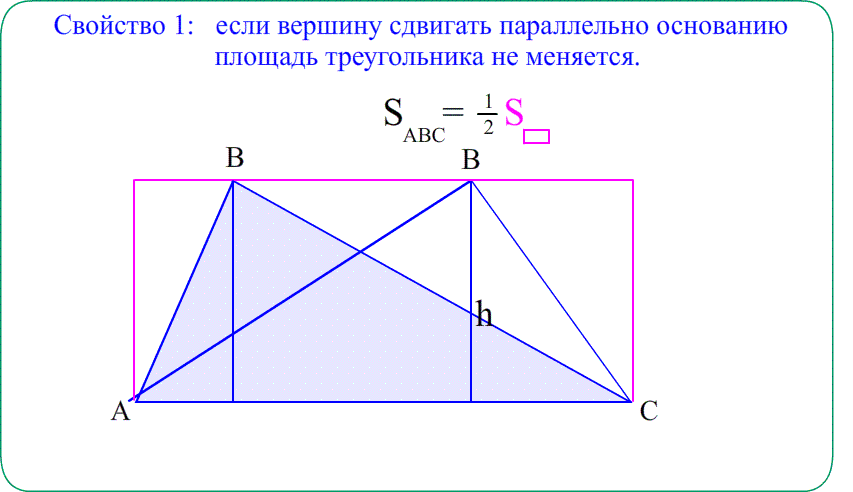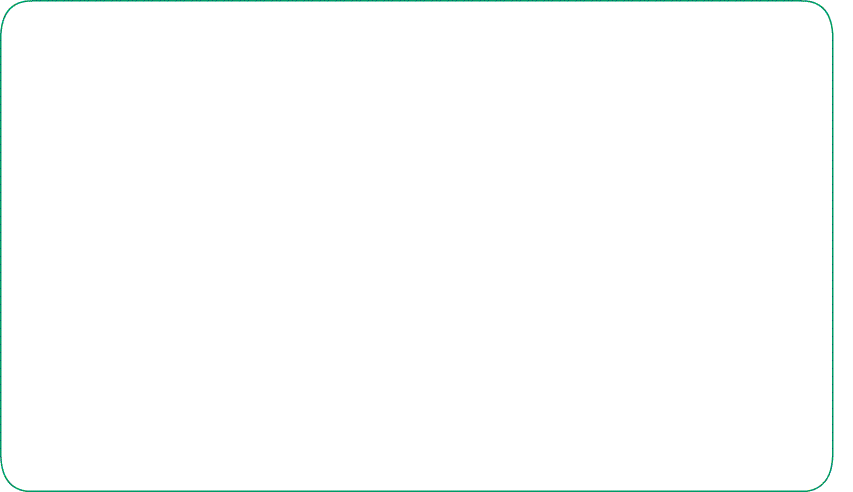
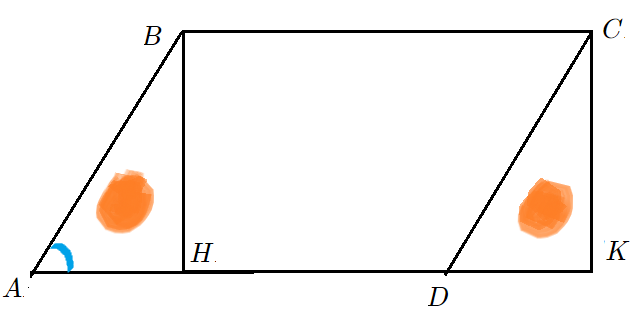
- Решение: Опустим высоты $BH$ и $CK$ на основание $AD$ . Они помогут “увидеть” площадь.
- Что есть синус $angle BAH$ в прямоугольном треугольнике $bigtriangleup ABH$? Отношение катета $BH$ к гипотенузе $AB$.
- Формула синуса позволит выразить высоту $BH$ через сторону $AB$ и синус $frac{1}{2}$. Высота $CK$ такая же.
- Параллелограмм $ABCD$ состоит из кусков: $bigtriangleup ABH$ и $4$-угольник $HBCD$. Площадь – сумма площадей кусков.
- Прямоугольник $HBCK$ состоит из кусков $HBCD$ и $bigtriangleup DCK$. Площадь также “сумма кусков”.
- Треугольники $bigtriangleup ABH$ и $bigtriangleup DCK$ одинаковые. Значит, параллелограмм и прямоугольник равновеликие.
- Площадь Параллелограмма $ABCD$ так же, как прямоугольника $HBCD$ равна высота на основание.
- $S_{ABCD}=S_{ABH}+S_{HBCD}=S_{HBCD}+S_{DCK}=S_{HBCK}=BHcdot HK=ABcdotsin angle BADcdot AD=7cdotfrac{1}{2}cdot10$
Теорема “о площади параллелограмма и треугольника через синус угла”:
- Площадь параллелограмма равна произведению сторон на синус угла параллелограмма:
- Формулы $S=acdot bcdotsin angle BAD$ $S_{ABCD}=ABcdot BCcdotsin D$
- Площадь треугольника равна половине произведения сторон треугольника на синус угла между ними.
- Формулы $S=frac{1}{2}cdot acdot bcdotsin angle C$ $S_{bigtriangleup ABC}=frac{1}{2}cdot ABcdot BCcdotsin angle CBA$
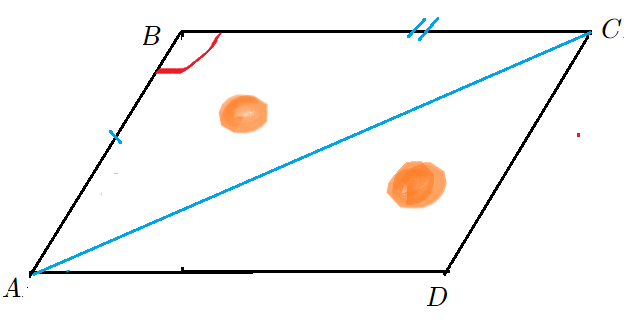
Площадь треугольника также легко получить через площадь параллелограмма, равновеликого с двумя треугольниками, приставленными друг к другу по диагонали. Тогда площадь одного треугольника будет равна половине площади параллелограмма с тем же основанием и с той же высотой.
Задача 2: Диагонали четырехугольника делятся точкой пересечения на отрезки $3$, $5$ и $6$, $7$ . Синус угла между диагоналями $0,2$. Найти площади треугольников и всего четырехугольника.
- Дано: $BO=3$ $OD=5$ $CO=6$ $AO=7$ … угол между $sinangle AOB=0,2$. Найти: $S_{ABCD}=?$.
- Решение: Диагонали делят четырехугольник на 4 треугольника. Площадь = сумме 4-х площадей.
- Аддитивность: $S_{ABCD}=S_{bigtriangleup AOB}+S_{bigtriangleup BOC}+S_{bigtriangleup COD}+S_{bigtriangleup AOD}$.
- Площадь одного из них по формуле: $S_{bigtriangleup AOB}=frac{1}{2}cdot AOcdot OBcdot sin angle AOB=frac{1}{2}cdot 7 cdot 3cdot 0,2=2,1$
- Каковы синусы остальных углов? Свойство: Синусы смежных углов равны: $sinangle BOC=sinangle COD=sinangle AOD=0,2$
- Тогда, площади других треугольников $frac{1}{2}cdot 3 cdot 6cdot 0,2=1,8$ $frac{1}{2}cdot 6 cdot 5cdot 0,2=3$ $frac{1}{2}cdot 5 cdot 7cdot 0,2=3,5$
- Площадь четырехугольника равна сумме этих площадей Ответ: $S_{ABCD}=2,1+1,8+3+3,5=10,4$
Теоретически, по-другому: Распишем получение площади $S_{ABCD}$ в буквах, без числовых значений:
- $frac{1}{2}cdot OAcdot OBcdot sin angle AOB+frac{1}{2}cdot OBcdot OCcdot sin angle AOB+frac{1}{2}cdot OCcdot ODcdot sin angle AOB+frac{1}{2}cdot ODcdot OAcdot sin angle AOB$
- Вынос за скобки множителей $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OAcdot OB+OBcdot OC+OCcdot OD+ODcdot OAright)$
- $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OBcdotleft(OA+OCright)+ODcdotleft(OA+OCright)right)=frac{1}{2}cdot sin angle AOBcdot AC cdot (OB+OD)$
- Получаем $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$ $Rightarrow$ $S_{ABCD}=frac{1}{2}cdot (7+6) cdot (3+5)cdot 0,2=13cdot 0,8=10,4$

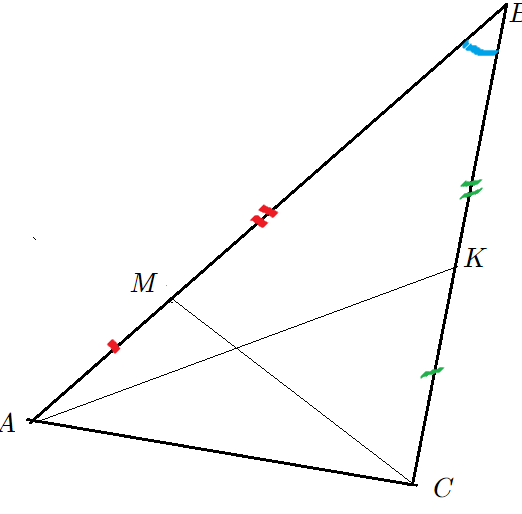
Задача 3: В треугольнике известны стороны $AB=10$ , $BC=12$ и угол $angle ABC=30$ . Точка $M$ делит сторону $AB$ в отношении 3 : 5, а точка $K$ делит сторону $BC$ в отношении 2 : 3. Найти площади и отношение площадей треугольников $ABK$ и $MBC$.
- Дано: $AB=10$, $BC=12$, $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$, $angle ABC=30$. Найти: $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=?$
- Точка делит отрезок в известном соотношении. Находим части как систему уравнений $frac{x}{y}=?$ $x+y=?$
- $frac{AM}{MB}=frac{3}{5}$, аддитивность $AM+MB=AB=10$ $Rightarrow$ $frac{AM}{AB}=frac{3}{3+5}$ $Rightarrow$ $AM=frac{15}{4}$, $MB=frac{25}{4}$
- $frac{BK}{KC}=frac{2}{3}$, $BK+KC=12$ из свойств пропорций $BK=frac{24}{5}$, $KC=frac{36}{5}$
- Найдем площадь через синус $S_{bigtriangleup ABK}=frac{1}{2}cdot AB cdot BK cdot sin angle ABC = frac{1}{2}cdot 10 cdot frac{24}{5} cdot sin 30= 24 cdot 0,5=12$
- В треугольнике $MBC$ тот же угол, $S_{bigtriangleup MBC}=frac{1}{2}cdot MB cdot BC cdot sin angle ABC = frac{1}{2}cdot frac{25}{4} cdot 12 cdot 0,5=frac{75}{4}$
- отношение площадей треугольников $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=frac{12}{frac{75}{4}}=frac{16}{25}$ Ответ: $frac{16}{25}$
Замечание, продолжение: Можно ли найти отношение площадей при неизвестных значениях сторон и угла?
- Зная лишь как делят точки $M$ и $K$ стороны треугольника, на какие пропорции ?!
- Дано только $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$. Выразим отрезки через стороны $AB$ и $BC$.
- Выразим площади $S_{bigtriangleup ABK}$ , $S_{bigtriangleup MBC}$ также через стороны $AB$ и $BC$ и угол $angle ABC$.
- Составим отношение площадей, выразим через стороны и угол. Что получится? Что можно сделать, ?
Теорема “о площади четырехугольника через диагонали и синус угла”:
- Площадь четырехугольника равна половине произведения диагоналей на синус угла между ними:
- Формулы $S=frac{1}{2}cdot d_1 cdot d_2 cdotsin angle alpha$ $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$
- Площадь ромба равна половине произведения диагоналей. … диагонали перпендикулярны!
- Формулы $S=frac{1}{2}cdot d_1 cdot d_2=frac{1}{2}cdot AC cdot BD$ $angle AOB=90$ $sin angle AOB=1$
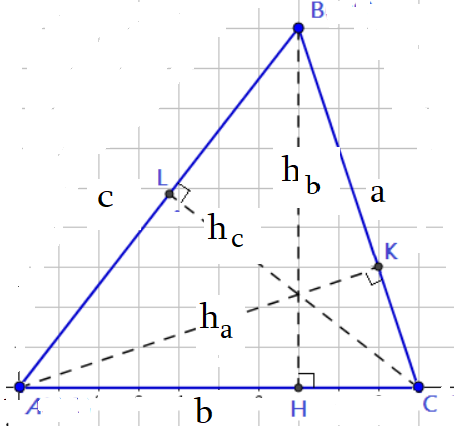
Формулы площади треугольника:
$S=frac{acdot h_a}{2}=frac{acdot bcdotsin C}{2}$ $S=frac{bcdot h_b}{2}=frac{bcdot ccdotsin A}{2}$ $S=frac{ccdot h_c}{2}=frac{ccdot acdotsin B}{2}$.
$sin A=frac{h_b}{c}=frac{h_c}{b}$ $sin B=frac{h_a}{c}=frac{h_c}{a}$ $sin C=frac{h_b}{a}=frac{h_a}{b}$.
$S_{ABC}=frac{1}{2}cdot ACcdot BCcdotsin C$ $S_{ABC}=frac{1}{2}cdot ABcdot BCcdotsin B$ $S_{ABC}=frac{1}{2}cdot ACcdot ABcdotsin A$ .
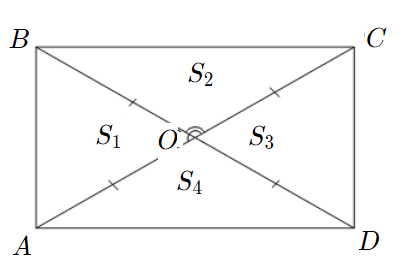
Задача 4: В прямоугольнике диагонали $10$ и угол между ними $30$. Найти площадь.
- Дано: $ABCD$ – прямоугольник , $AC=10$ , $angle AOB=30$ Найти: $S_{ABCD}$ .
- Решение: В прямоугольнике диагонали равны и пересекаются по середине $AO=OB=5$
- $bigtriangleup AOB$ и $bigtriangleup COD$ равные $Rightarrow$ $S_1=S_3$ ;
- $bigtriangleup BOC$ и $bigtriangleup AOD$ равные $Rightarrow$ $S_2=S_4$ .
- Смежные, $angle BOC=180-angle AOB=150$. Найдем отношение $frac{S_1}{S_2}=frac{frac{1}{2}AOcdot OBcdotsin30}{frac{1}{2}BOcdot OCcdotsin150}$
- $sin30=sinleft(180-30right)=sin150$. тогда $frac{S_1}{S_2}=frac{frac{1}{2}cdot5cdot5cdotsin150}{frac{1}{2}cdot5cdot5cdotsin150}=1$ Значит, $S_1=S_2$
- Аналогично: $frac{S_3}{S_4}=frac{frac{1}{2}DOcdot OCcdotsin30}{frac{1}{2}AOcdot ODcdotsin150} =1$ $Rightarrow$ $S_3=S_4$, площади равные.
- Диагонали рассекают прямоугольник на четыре равновеликих: треугольника $S_1=S_2=S_3=S_4$ .
- … тогда, по свойству аддитивности площадей $S_1=S_2=S_3=S_4=frac{1}{4}S_{ABCD}$ .
- $S_{AOB}=S_1=frac{1}{2}AOcdot OBcdot sin 30=frac{1}{2}cdot 5cdot 5cdot frac{1}{2}=frac{25}{4}$ $Rightarrow$ $S_{ABCD}=4cdotfrac{25}{4}$
- Найдя площадь АОВ, нашли площадь прямоугольника умножением на 4. Ответ: $S_{ABCD}=25$
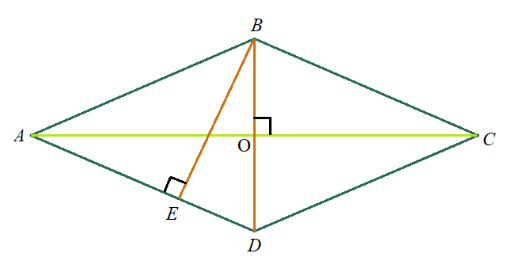
Задача 5: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Дано: ромб $ABCD$ , $BD=13$, высота $EB=12$ , Найти: $S_{ABCD}$ .
- Решение: прямоугольный $bigtriangleup BED$, подобен тем, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Одинаковый “состав” углов. Все прямоугольные,
- Прямоугольный $bigtriangleup BED$, по Пифагору выразим катет $DE=sqrt{BD^2-BE^2}=5$
- Диагонали в ромбе делятся пополам: $BO=OD=frac{BD}{2}=6,5$ $AO=frac{AC}{2}$ $AC=2cdot AO$
- Для нахождения площади ромба нам нужно найти вторую диагональ.
- $bigtriangleup BED sim bigtriangleup AOD$ $Rightarrow$ $frac{AO}{BE}=frac{OD}{ED}$ $Rightarrow$ $AO=frac{ODcdot BE}{ED}=frac{6,5cdot 12}{5}=15,6$ $AC=2cdot AO=31,2$
- Ответ: Площадь ромба через диагонали: $S_{ABCD}=frac{1}{2}cdot ACcdot BD=0,5cdot 31,2cdot13=202,8$


Задача 6. Площадь равнобедренного треугольника равна $100$ , а угол при вершине $30^o$ 1) Найти его боковые стороны . 2) Найти тригонометрию $15^o$
- Решение: 1) Известны площадь и угол, значит используем формулу площади через синус $30^o$ .
- Пусть боковая сторона $a$ , $S=frac{1}{2}acdot acdotsin30$ , тогда $100=frac{1}{2}a^2cdotsin30$ $Leftrightarrow$ $100=frac{1}{2}a^2cdotfrac{1}{2}$ $Rightarrow$
- $a=sqrt{400}=20$ Ответ: $a=20$
- 2) По теореме косинусов найдем основание $c=sqrt{a^2+a^2-2cdot acdot acdotfrac{sqrt{3}}{2}}=asqrt{2-sqrt{3}}$
- Из вершины равнобедренного угла проведем биссектрису к основанию. По свойству равнобедренности
- она будет и высотой $h$ (треугольник поделится на 2 прямоугольных с углами 15 градусов) и медианой,
- а значит основание поделится пополам , как и угол 30 у вершины поделится по 15 градусов.
- По прямоугольнему треугольнику (половинка): $sin15=frac{0,5cdot c}{a}=frac{0,5cdot acdotsqrt{2-sqrt{3}}}{a}=frac{sqrt{2-sqrt{3}}}{2}$
- Площадь через основание $S=frac{1}{2}cdot ccdot h$, найдем высоту $h=frac{2cdot S}{c}=frac{2cdot0,5cdot a^2cdotsin30}{acdotsqrt{2-sqrt{3}}}=frac{a}{2cdotsqrt{2-sqrt{3}}}$
- В прямоугольном треугольнике стороны $h$, $frac{c}{2}$, $a$. Тогда $cos15=frac{h}{a}=frac{frac{a}{2cdotsqrt{2-sqrt{3}}}}{a}=frac{1}{2cdotsqrt{2-sqrt{3}}}$
Интерактивные Упражнения
Площадь параллелограмма можно найти по стороне и проведённой к этой стороне высоте, по двум сторонам и углу, по диагоналям и углу между ними.
I. Площадь параллелограмма по стороне и высоте
Площадь параллелограмма равна произведению стороны параллелограмма на высоту, проведённую к этой стороне.
Формула для нахождения площади параллелограмма через сторону и высоту:
![]()
 Например,площадь параллелограмма ABCD через высоту можно найти по одной из формул:
Например,площадь параллелограмма ABCD через высоту можно найти по одной из формул:
![]()
или

![]()
II. Площадь параллелограмма по сторонам и углу
Площадь параллелограмма равна произведению его сторон на синус угла между ними.
Формула для нахождения площади параллелограмма через стороны и угол:
![]()
 Например, площадь параллелограмма ABCD
Например, площадь параллелограмма ABCD
![]()
По свойствам параллелограмма, противоположные углы параллелограмма равны:
![]()
![]()
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º, то есть,
![]()
![]()
А так как синус тупого угла равен синусу смежного ему угла, то
![]()
![]()
Таким образом, площадь параллелограмма можно найти как произведение его двух любых не смежных сторон на синус любого угла.
III. Площадь параллелограмма по диагоналям
Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
Формула площади параллелограмма через диагонали:
![]()
 Например, площадь параллелограмма ABCD
Например, площадь параллелограмма ABCD
![]()
А так как
![]()
то в качестве угла между диагоналями можно брать любой угол — как острый, так и тупой (прямой — в ромбе и квадрате).
В прошлой статье предложила решить 4 задачки на тему площадь параллелограмма. Задания простые. Несколько заданий требуют несложных размышлений.
Посмотрим как они решаются.
Во всех четырех задачах требуется найти площадь параллелограмма ABCD.
Задание №1
Задание на знание базовой формулы нахождения площади параллелограмма (произведение высоты и стороны параллелограмма, к которой эта высота проведена):
Высота, в данном случае, отрезок ВЕ, а сторона, к которой проведена высота это AD.
В параллелограмме противолежащие стороны равны. Значит AD=BC=8.
ОТВЕТ: 32
Задание №2
В этом задании уже понадобится знание формулы вычисления площади параллелограмма через синус угла (площадь параллелограмма вычисляется как произведение смежных сторон на синус угла между ними):
Остается только найти угол между сторонами параллелограмма из исходных данных.
Заметим, что углы BCA и CAD накрест лежащие углы при параллельных прямых ВС и AD и секущей АС .
Тогда из рисунка видно, что угол BAD является суммой углов BAC и CAD:
Не забываем, что AD=ВС=12. Остается только подставить все значения в формулу и найти площадь.
Синус угла 60 градусов – табличное значение.
ОТВЕТ: 60√3
Задание №3
В этом задании знаем высоты, но не знаем ни одной стороны. Попробуем найти любую из сторон параллелограмма.
Рассмотрим образовавшийся прямоугольный треугольник ВАЕ:
В этом треугольнике один острый угол равен 60 градусов, значит второй острый угол равен 90-60=30 градусов.
А в прямоугольном треугольнике против угла 30 градусов лежит катет равный половине гипотенузы. Т.е. гипотенуза АВ в два раза больше противолежащего катета ВЕ:
Не забываем что в параллелограмме CD=AB=8. Воспользуемся формулой вычисления площади параллелограмма:
где BF – высота, СD – сторона, к которой проведена высота.
ОТВЕТ: 48
Задание №4
Сторона параллелограмма по сути нам известна (AD=AE+ED=10+4=14).
Попробуем найти высоту.
Для этого сначала посмотрим на образовавшийся выпуклый четырехугольник BEDF, в котором два угла прямые. С учетом, что сумма углов выпуклого четырехугольника равна 360 градусов, можно найти угол FDE (или тот же угол CDA, обозначенный другими буквами ):
Помним, что сумма углов параллелограмма, прилежащих одной стороне, равна 180 градусов. Значит:
Рассмотрим треугольник АВЕ (прямоугольный). Если один его острый угол равен 45 градусов, то второй:
По признаку равнобедренного треугольника получаем, что треугольник АВЕ – равнобедренный с равными сторонами АЕ и ВЕ:
ВЕ, в свою очередь, является высотой параллелограмма АВСD. Значит:
ОТВЕТ: 140
Если вы знаете того, кто готовится к ОГЭ не забудьте поделиться с ним этой информацией. Всегда пригодится.
Продолжение следует…
Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность
(✿◠‿◠)
Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.
-
Формула вычисления площади
- По длине стороны и высоте
- По двум сторонам и углу между ними
- По двум диагоналям и углу между ними
- Примеры задач
Формула вычисления площади
По длине стороны и высоте
Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h

По двум сторонам и углу между ними
Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:
S = a ⋅ b ⋅ sin α

По двум диагоналям и углу между ними
Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:
S = 1/2 ⋅ d 1 ⋅ d 2 ⋅ sin α

Примеры задач
Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.
Решение:
Используем первую формулу, в которой задействованы известные нам по условиям задания значения: S = 4 см * 7 см = 28 см2.
Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.
Решение:
Применим вторую формулу, рассмотренную выше: S = 6 см * 8 см * sin 30° = 24 см2.
Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.
Решение:
Воспользуемся формулой, в которой фигурируют диагонали: S = 1/2 * 4 см * 6 см * sin 90° = 12 см2.