Версия для печати и копирования в MS Word
1
Тип 17 № 91
i
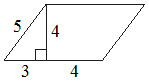
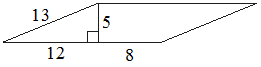
Найдите площадь параллелограмма, изображённого на рисунке.
2
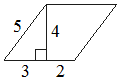
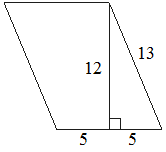
Найдите площадь параллелограмма, изображённого на рисунке.
3
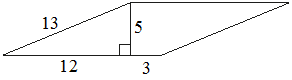
Найдите площадь параллелограмма, изображённого на рисунке.
4
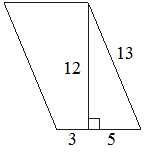
Найдите площадь параллелограмма, изображённого на рисунке.
5
Найдите площадь параллелограмма, изображённого на рисунке.
Источник: Банк заданий ФИПИ
6
Найдите площадь параллелограмма, изображённого на рисунке.
Источник: Банк заданий ФИПИ
7
Найдите площадь параллелограмма, изображенного на рисунке.
8
Найдите площадь параллелограмма, изображённого на рисунке.
Источник: Банк заданий ФИПИ
9
Найдите площадь параллелограмма, изображённого на рисунке.
Источник: Банк заданий ФИПИ
10
Найдите площадь параллелограмма, изображённого на рисунке.
Источник: Банк заданий ФИПИ
11
Найдите площадь параллелограмма, изображённого на рисунке
Источник: Банк заданий ФИПИ
12
Найдите площадь параллелограмма, изображённого на рисунке.
Источник: Банк заданий ФИПИ
13
Найдите площадь параллелограмма, изображённого на рисунке.
Источник: Банк заданий ФИПИ
14
Найдите площадь параллелограмма, изображенного на рисунке.
15
Найдите площадь параллелограмма, изображенного на рисунке.
Здравствуйте, дорогие читатели. В этом выпуске рассмотрим задачи на вычисление площади параллелограмма и трапеции. Начнем с самой простой задачи, которая не требует знания формулы.
Задача №1
Решение:
Для решения этой задачи, знание формул не требуется, то необходимо провести прямую через точку Е параллельно сторонам ВС и AD.
Так как Е – середина АВ, то ЕN – делит параллелограмм на два равных параллелограмма AEND и EBCN. Проведя во втором параллелограмме диагональ, у нас получится четыре равных по площади треугольника.
В такой задаче возможен вопрос, где нужно найти площадь трапеции AECD. Тогда 33*3=99
Задача №2 Найдите площадь параллелограмма, изображённого на рисунке:
Внимание! В таких задачах будьте внимательны, всегда есть лишние данные.
Задание №3
Решение: Для решения такой задачи из формулы площади параллелограмма S=ah, найдем обе высоты.
Наибольшая высота равна 4
Задание №4
Решение:
Площадь трапеции вычисляем по формуле:
Важно! В трапеции часто нужно проводить две высоты. В нашем случае также проведем две высоты. Так как трапеция равнобедренная, то после проведения высот, получим два прямоугольных треугольника с равными катетами.
Задача №5
Важно! Чертите ромб так, как параллелограмм, задачи будут решаться легко.
В этой задаче применили формулу площади параллелограмма, изучаемую в 9 классе: площадь параллелограмма равна произведению двух смежных сторон на синус угла между ними.
Так же можно воспользоваться формулой из 8 класса: S=ah, но в этом случае придется находить высоту параллелограмма ВН.
Треугольник АВН прямоугольный, ВН – катет, лежащий против угла в 30 градусов, равен половине гипотенузы. ВН=3:2=1,5; Sромба=3*1.5=4.5
Задача №6. Найдите площадь ромба, если его диагонали равны 19 и 6
В этой задаче воспользуемся формулой площади ромба: Площадь ромба равна половине произведению его диагонали.
А как легко запомнить формулы читайте здесь
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Среди задач на вычисление площади параллелограмма из открытого банка ФИПИ есть и е, на которые достаточно краткого ответа, и с развернутым ответом. И те, и другие, перед вами. Любое из них может вам попасться на экзамене в этом году.
Вспоминаем, что площадь параллелограмма равна произведению длины основания на высоту:
S = ah
Реальные задания по геометрии из банка ФИПИ
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+7) * 4 = 40Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.
Ответ: 40
E8FC9F
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+4) * 4 = 28Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.
Ответ: 28
5AEBBA
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+2) * 4 = 20Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.
Ответ: 20
460490
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+8) * 4 = 44Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.
Ответ: 44
29D63A
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (12+3) * 5 = 75Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.
Ответ: 75
D97D85
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+5) * 12 = 96Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.
Ответ: 96
B08979
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (12+8) * 5 = 100Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.
Ответ: 100
956EDE
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (5+5) * 12 = 120Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.
Ответ: 120
66228A
Задания второй части ОГЭ с расширенным решением
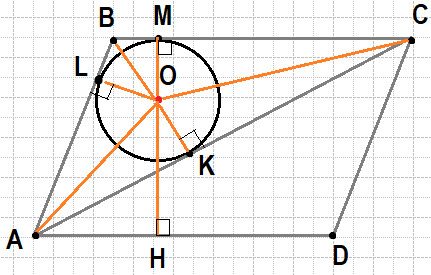
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:AK=$sqrt{AO^2+ОК^2}=;sqrt{25-9}$ = 4
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 4.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{4+4+2BM+2MC}2ast3=3ast(4+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(3+4)ast(BM+MC)=7ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$frac{7ast(BM+MC)}2=3;ast;(;4;+;B;M;+;M;C)\7ast(BM+MC);=;6;ast;(;4;+;B;M;+;M;C)\7ast(BM+MC);=;24;+;6;ast;(B;M;+;M;C)\7ast(BM+MC);-;6;ast;(B;M;+;M;C);=;24\B;M;+;M;C;=;24\\\$
То есть основание BC = 24.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(3+4)*24=168Ответ: 168
701E1F
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 6 и 5. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:AK=$sqrt{AO^2+ОК^2}=;sqrt{169-25}$ = 12
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{12+12+2BM+2MC}2ast5=5ast(12+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(6+5)ast(BM+MC)=11ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$frac{11ast(BM+MC)}2=5ast(12+BM+MC)\11ast(BM+MC);=;10ast(12+BM+MC)\11ast(BM+MC);=;120;+;10ast(BM+MC)\11ast(BM+MC);-;10;(BM+MC);=;120\B;M+M;C;=;120\\\$
То есть основание BC = 120.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+6)*120=1320Ответ: 1320
B520E8
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 7 и 5. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:AK=$sqrt{AO^2+ОК^2}=;sqrt{169-25}$ = 12
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{12+12+2BM+2MC}2ast5=5ast(12+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(7+5)ast(BM+MC)=12ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$frac{12ast(BM+MC)}2=5ast(12+BM+MC)\12ast(BM+MC);=;10ast(12+BM+MC)\12ast(BM+MC);=;120;+;10ast(BM+MC)\12ast(BM+MC);-;10;(BM+MC);=;120\2ast(BM+MC);=;120\BM+MC;=;60\\\\$
То есть основание BC = 60.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(7+5)*60=720Ответ: 720
7AFAA8
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 8 и 5. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:AK=$sqrt{AO^2+ОК^2}=;sqrt{169-25}$ = 12
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{12+12+2BM+2MC}2ast5=5ast(12+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(8+5)ast(BM+MC)=13ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$frac{13ast(BM+MC)}2=5ast(12+BM+MC)\13ast(BM+MC);=;10ast(12+BM+MC)\13ast(BM+MC);=;120;+;10ast(BM+MC)\13ast(BM+MC);-;10;(BM+MC);=;120\3ast(BM+MC);=;120\BM+MC;=;40\\\\$
То есть основание BC = 40.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+8)*40=520Ответ: 520
15838B
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:AK=$sqrt{AO^2+ОК^2}=;sqrt{169-25}$ = 12
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{12+12+2BM+2MC}2ast5=5ast(12+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(9+5)ast(BM+MC)=14ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$frac{14ast(BM+MC)}2=5ast(12+BM+MC)\14ast(BM+MC);=;10ast(12+BM+MC)\14ast(BM+MC);=;120;+;10ast(BM+MC)\14ast(BM+MC);-;10;(BM+MC);=;120\4ast(BM+MC);=;120\BM+MC;=;30\\\\$
То есть основание BC = 30.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+9)*30=420Ответ: 420
221DAD
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:AK=$sqrt{AO^2+ОК^2}=;sqrt{625-49}$ = 24
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{24+24+2BM+2MC}2ast7=7ast(24+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(13+7)ast(BM+MC)=20ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$frac{20ast(BM+MC)}2=7ast(24+BM+MC)\20ast(BM+MC);=;14ast(24+BM+MC)\20ast(BM+MC);=;336;+;14ast(BM+MC)\20ast(BM+MC);-;14;(BM+MC);=;336\6ast(BM+MC);=;336\BM+MC;=;56\\\\$
То есть основание BC = 56.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(13+7)*56=1120Ответ: 1120
716CE8
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 14 и 7. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:AK=$sqrt{AO^2+ОК^2}=;sqrt{625-49}$ = 24
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{24+24+2BM+2MC}2ast7=7ast(24+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(14+7)ast(BM+MC)=21ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$frac{21ast(BM+MC)}2=7ast(24+BM+MC)\21ast(BM+MC);=;14ast(24+BM+MC)\21ast(BM+MC);=;336;+;14ast(BM+MC)\21ast(BM+MC);-;14;(BM+MC);=;336\7ast(BM+MC);=;336\BM+MC;=;48\\\\$
То есть основание BC = 48.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(14+7)*48=1008Ответ: 1008
A4192E
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 15 и 7. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:AK=$sqrt{AO^2+ОК^2}=;sqrt{625-49}$ = 24
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{24+24+2BM+2MC}2ast7=7ast(24+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(15+7)ast(BM+MC)=22ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$frac{22ast(BM+MC)}2=7ast(24+BM+MC)\22ast(BM+MC);=;14ast(24+BM+MC)\22ast(BM+MC);=;336;+;14ast(BM+MC)\22ast(BM+MC);-;14;(BM+MC);=;336\8ast(BM+MC);=;336\BM+MC;=;42\\\\$
То есть основание BC = 42.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(15+7)*42=924Ответ: 924
2E555E
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 17 и 7. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:AK=$sqrt{AO^2+ОК^2}=;sqrt{625-49}$ = 24
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{24+24+2BM+2MC}2ast7=7ast(24+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(17+7)ast(BM+MC)=24ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$frac{24ast(BM+MC)}2=7ast(24+BM+MC)\24ast(BM+MC);=;14ast(24+BM+MC)\24ast(BM+MC);=;336;+;14ast(BM+MC)\24ast(BM+MC);-;14;(BM+MC);=;336\10ast(BM+MC);=;336\BM+MC;=;33,6\\\\$
То есть основание BC = 33,6.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(17+7)*33,6=806,4Ответ: 806,4
DFC86B
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 19 и 7. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:AK=$sqrt{AO^2+ОК^2}=;sqrt{625-49}$ = 24
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{24+24+2BM+2MC}2ast7=7ast(24+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(19+7)ast(BM+MC)=26ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$frac{26ast(BM+MC)}2=7ast(24+BM+MC)\26ast(BM+MC);=;14ast(24+BM+MC)\26ast(BM+MC);=;336;+;14ast(BM+MC)\26ast(BM+MC);-;14;(BM+MC);=;336\12ast(BM+MC);=;336\BM+MC;=28\\\\$
То есть основание BC = 28.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(19+7)*28=728Ответ: 728
1D6569
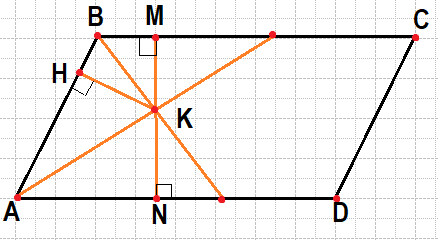
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=7.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=7.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =19*(7+7)=19*14=266.
Ответ: 266
97C87B
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=3.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=3.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =11*(3+3)=11*6=66.
Ответ: 66
F8A0E6
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=9.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=9.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =12*(9+9)=12*18=216.
Ответ: 216
67503F
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 10.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=10.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=10.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =19*(10+10)=19*20=380.
Ответ: 380
D60F99
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=17, а расстояние от точки K до стороны AB равно 10.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=10.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=10.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =17*(10+10)=17*20=340.
Ответ: 340.
B435D4
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=18, а расстояние от точки K до стороны AB равно 1.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=1.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=1.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =18*(1+1)=18*2=36.
Ответ: 36
E097F7
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=7, а расстояние от точки K до стороны AB равно 4.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=4.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=4.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =7*(4+4)=7*8=56.
Ответ: 56
80A169
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 8.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=8.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=8.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =2*(8+8)=2*16=32.
Ответ: 32
569075
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=6, а расстояние от точки K до стороны AB равно 6.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=6.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=6.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =6*(6+6)=6*12=72.
Ответ: 72
FD6657
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 1.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=1.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=1.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =2*(1+1)=2*2=4.
Ответ: 4
A7594E
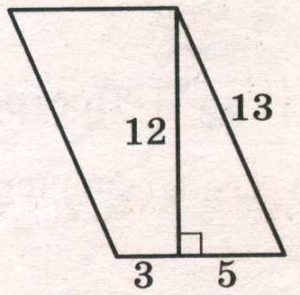
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Высота параллелограмма равна 12. Основание к которой проведена высота равно:
3 + 5 = 8
Площадь параллелограмма равна:
S = a·h = 8·12 = 96
Ответ: 96.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.8 / 5. Количество оценок: 26
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Рассмотрим несколько задач на данную тему.
| #1 | #2 | #3 | #4 | #5 |
Задача #1
(Номер задачи на fipi.ru — 71E23E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Прежде чем приступать к решению задачи, вспомним теорию >>
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Площадь параллелограмма вычисляется по формуле:
где a — основание параллелограмма, h — высота параллелограмма.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 7, а высота: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 28 ед. кв.
Задача #2
(Номер задачи на fipi.ru — 3BD9B6). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 15 ед. кв.
Задача #3
(Номер задачи на fipi.ru — 5C5046). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 20 ед. кв.
Задача #4
(Номер задачи на fipi.ru — 566A4E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 18 ед. кв.
Задача #5
(Номер задачи на fipi.ru — 0275CC). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 6.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 36 ед. кв.