
{S = a cdot h}
Найти площадь параллелограмма
На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные – основание, высоту, стороны, диагонали и углы между ними и получите ответ.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Содержание:
- калькулятор площади параллелограмма
- формула площади параллелограмма через сторону и высоту
- формула площади параллелограмма через две стороны и угол между ними
- формула площади параллелограмма через диагонали и угол между ними
- примеры задач
Формула площади параллелограмма через сторону и высоту
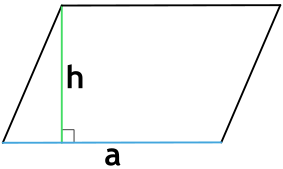
{S = a cdot h}
a – сторона параллелограмма
h – высота параллелограмма
Формула площади параллелограмма через две стороны и угол между ними

{S=a cdot b cdot sin(alpha)}
a, b – стороны параллелограмма
α – угол между сторонами a и b
Формула площади параллелограмма через диагонали и угол между ними
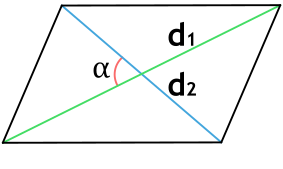
{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}
d1, d2 – диагонали параллелограмма
α – угол между диагоналями
Примеры задач на нахождение площади параллелограмма
Задача 1
Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.
Решение
Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.
S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Мы можем проверить ответ с помощью калькулятора .
Задача 2
Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.
Решение
Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.
S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2
Ответ: 48 см²
И снова проверить ответ нам поможет калькулятор .
Задача 3
Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.
Решение
В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.
S = a cdot h = 12 cdot 8 = 96 : см^2
Ответ: 96 см²
И снова проверить ответ нам поможет калькулятор .
Как найти площадь параллелограмма — три основных формулы
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья на еще одну математическую тему. Мы расскажем, как правильно посчитать площадь параллелограмма. Эту тему подробно изучают только в 8-м классе. И это говорит, что она не такая простая.

Но для начала давайте все-таки напомним, какая фигура называется параллелограммом.
Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.
Классический параллелограмм выглядит вот так:

Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.
Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.

И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».
Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.
Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.
Формулы для расчета площади параллелограмма
Есть три основных формулы для вычисления площади параллелограмма:
- если известна длина стороны и высота, проведенная к ней;
- если известны длины сторон и углы между ними;
- если известны длины диагоналей и угол между ними.
Теперь о каждом из этих способов подробнее.
Как найти площадь параллелограмма, если известны сторона и высота
Возьмем для примера такой параллелограмм:
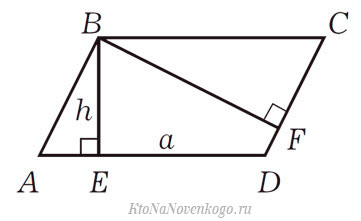
В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.
В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.
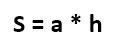
И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.
Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:
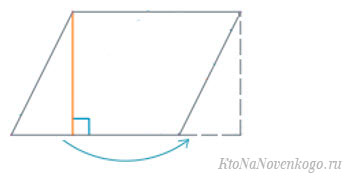
В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.
Формула площади параллелограмма, если известны стороны и угол
Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.
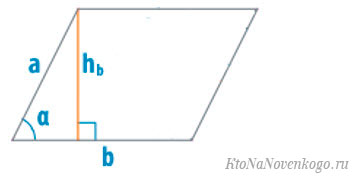
Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.
Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:
![]()
Соответственно, чтобы посчитать значение высоты надо:
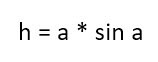
И наша конечная формула для расчета площади будет выглядеть следующим образом:
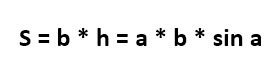
Как найти площадь параллелограмма через диагонали
Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.
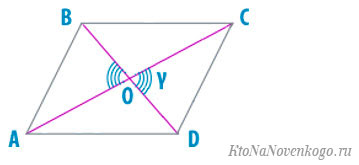
В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:
![]()
Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.
Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.
Как найти площадь параллелограмма
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти площадь параллелограмма
Чтобы найти площадь параллелограмма воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
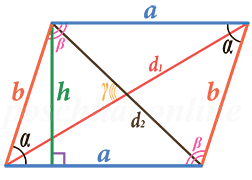
Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны друг другу.
Узнать чему равна площадь параллелограмма (S) можно зная (либо-либо):
- длину стороны a и длину высоты h
- длины сторон a и b, и угол α
- длины сторон a и b, и угол β
- длины сторон a и b, и длину любой из диагоналей (d1 или d2)
- длины диагоналей d1 и d2, и угол между ними γ
Подставьте значения в соответствующие поля и получите результат.
Зная длину стороны a и длину высоты h
Чему равна площадь параллелограмма если сторона
a = ,
а высота
h = ?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длина стороны a и длина высоты h, проведенной к этой стороне?
Формула
S = a⋅h
Пример
Если сторона параллелограмма a = 8 см, а высота h = 4 см, то:
S = 8 ⋅ 4 = 32 см2
Зная длины сторон a и b, и угол α
Чему равна площадь параллелограмма если сторона
a = ,
сторона
b = ,
а угол между ними
α = °
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними α?
Формула
S = a⋅b⋅sinα
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠α = 50° то:
S = 8 ⋅ 5 ⋅ sin 50 = 40 ⋅ 0.766 ≈ 30.64 см2
Зная длины сторон a и b, и угол β
Чему равна площадь параллелограмма если сторона
a = ,
сторона
b = ,
а угол между ними
β = °
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними β?
Формула
S = a⋅b⋅sin(180 – β)
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠β = 130° то:
S = 8 ⋅ 5 ⋅ sin(180-130) = 40 ⋅ 0.766 ≈ 30.64 см2
Зная длины сторон a и b, и длину диагонали (d1 или d2)
Чему равна площадь параллелограмма если сторона
a = ,
сторона
b = ,
а диагональ
d =
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины сторон a и b, и длина любой из диагоналей d?
Формула
S = 2√p⋅(p-a)⋅(p-b)⋅(p-d), где p=(a+b+d)/2
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а диагональ d = 11 см то:
p = (8 + 5 +11)/2 = 12
S = 2√12⋅(12-8)⋅(12-5)⋅(12-11) = 2⋅√12⋅4⋅7⋅1 = 2⋅√336 = 36.66 см2
Зная длины диагоналей d1 и d2, и угол между ними γ
Чему равна площадь параллелограмма если диагональ
d1 = ,
диагональ
d2 = ,
а угол между ними
γ = °
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины диагоналей d1 и d2, и угол между ними γ?
Формула
S = ½⋅d1⋅d2⋅sinγ
Пример
Если диагональ параллелограмма d1 = 11 см, диагональ d2 = 7 см, а ∠γ = 45° то:
S = ½ ⋅ 11 ⋅ 7 ⋅ sin 45 = 38.5 ⋅ 0.7071 ≈ 27.22 см2
См. также
В этой статье будет раскрыта одна из математических тематик. Вы узнаете, как найти площадь параллелограмма. Данную тематику преподают в восьмом классе. Тем, кто не разобрался с ней, будет полезна эта статья.
Содержание
- Как найти площадь параллелограмма – свойства фигуры
- Расчет площади параллелограмма, если известны стороны, высота
- Расчет площади параллелограмма по диагоналям
- Расчет площади параллелограмма, если известны стороны, угол
- Видео: Площадь параллелограмма
В школе бывает так, что учитель объясняет урок, а дети не понимают. Потому дальше выходит, что ребенок не усваивает не только одну тему, а и те, что идут дальше. Особенно в геометрии. Ведь многие доказательства выводятся на основании правил и предыдущих теорем. Дальше узнаем, как найти площадь параллелограмма. Но изначально для того, чтобы узнать площадь, следует знать определение, что такое параллелограмм. Эта фигура представляет собой четырехугольник с параллельными сторонами и равными противоположными углами. Теперь давайте найдем площадь фигуры разными методами.
Как найти площадь параллелограмма – свойства фигуры
Итак, параллелограмм выглядит следующим образом:

Еще древнегреческий ученый математики Евклид описал несколько свойств данной фигуры в книге «Начала». А точнее две характеристики параллелограмма:
- фигуру можно сравнить и с прямоугольником, ведь все напротив лежащие стороны ее параллельны, равны, еще и пересекаются под углами 90°.
- также правило применимо и к квадрату, ромбу, отличие лишь в углах.
ВАЖНО: Прежде, чем приступить к доказательству, определимся с термином – площадь. Площадью называется размер самой фигуры, точнее плоскость занятая ею, что ограничивается самими сторонами данной фигуры.
Эти свойства недаром описаны выше, благодаря им будет легче узнать, как рассчитывать S – площадь фигуры.
Имеется несколько базовых формул, чтобы вычислить S – площадь параллелограмма:
- Когда даны: высота и длина параллелограмма
- Когда даны: длина одной и другой стороны фигуры, углы фигуры
- Когда даны: размеры обеих диагоналей, один из углов их пересечения.
Теперь о каждом из этих способов подробнее.
Расчет площади параллелограмма, если известны стороны, высота
Чтобы рассчитать величину S фигуры (площадь параллелограмма), следует знать все ее свойства. Выше уже были рассмотрены эти правила. Итак, первая формула – это нахождение площади фигуры по стороне и высоте. Пусть ВН – высота, а АВ – сторона. Высоту проводят на основание под углом 90º.

Выше предоставлено доказательство данной аксиомы. Из него видно, что S = a • h. Кстати, площадь измеряют в квадратных единицах.
S = АВ • ВН, для начала вывода теоремы следует рассмотреть треугольники, образовавшиеся в результате проведения высот к одному и тому же основанию. Они между собой будут равны. Ну и тогда площадь прямоугольника образовавшегося будет равна площади параллелограмма. А ранее было доказано, что в S прямоугольника = a • h. Именно поэтому и параллелограмм будет иметь такую же формулу для вычисления площади.
Расчет площади параллелограмма по диагоналям
Найти площадь параллелограмма можно различными методами. И этот вариант является распространенным. Для того, чтобы рассчитать S следует знать величину угла и длины диагоналей параллелограмма. Эта аксиома тоже важна в геометрии, зная ее вы с легкостью сможете решить задачи на контрольных и самостоятельных работах.

Для доказательства следует рассмотреть два равных треугольника, что получились при разделении параллелограмма на две части.

По трем сторонам. Значит и углы в этих треугольниках равны, смотрите рисунок выше. А площадь треугольника равняется половине произведения стороны a на высоту h. А высота в данных треугольниках – это и есть диагональ параллелограмма. Отсюда и выходит, что S параллелограмма равняется площади этих двух треугольников или 1/2 sin α на произведение диагоналей.
- S = 1/2 • sin α • d1 • d2
Что и требовалось найти.
Расчет площади параллелограмма, если известны стороны, угол
Если вы знаете чему равны длины обеих сторон, угол, то сможете найти и S параллелограмма. Площадь параллелограмма в этом случае равна:
- S = b • a • sin∠α.
Для того, чтобы доказать данную аксиому, достаточно по формулам найти высоту фигуры и подставить найденные данные в известную формулу параллелограмма.

По правилам геометрии, если рассматривать треугольники, то sin угла будет равен отношению противолежащего h – катета к гипотенузе. А вот катет, это и есть высота фигуры. Вот и выходит:
- sin β = h/a
Из этого равенства можно высчитать, чему равняется высота:
- h = sin β • a
Теперь остается подставить все элементы в формулу и выйдет следующее:
- S параллелограмма = h • b • sin β
Видео: Площадь параллелограмма
1. Формула площади параллелограмма через стороны и углы

a, b – стороны параллелограмма
α, β – углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):

Калькулятор – вычислить, найти площадь параллелограмма:
a(сторона)=
b(сторона)=
α или β (угол в градусах)= ( sin α=sin β )
S=
2. Формула площади параллелограмма через сторону и высоту

a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D – большая диагональ
d –меньшая диагональ
α, β – углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):

Калькулятор – вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
