Как найти площадь параллелограмма огэ 9 класс

В прошлой статье предложила решить 4 задачки на тему площадь параллелограмма. Задания простые. Несколько заданий требуют несложных размышлений.

Посмотрим как они решаются.

Во всех четырех задачах требуется найти площадь параллелограмма ABCD.

Задание №1

Задание на знание базовой формулы нахождения площади параллелограмма (произведение высоты и стороны параллелограмма, к которой эта высота проведена):

Высота, в данном случае, отрезок ВЕ, а сторона, к которой проведена высота это AD.

В параллелограмме противолежащие стороны равны. Значит AD=BC=8.

ОТВЕТ: 32

Задание №2

В этом задании уже понадобится знание формулы вычисления площади параллелограмма через синус угла (площадь параллелограмма вычисляется как произведение смежных сторон на синус угла между ними):

Остается только найти угол между сторонами параллелограмма из исходных данных.

Заметим, что углы BCA и CAD накрест лежащие углы при параллельных прямых ВС и AD и секущей АС .

Тогда из рисунка видно, что угол BAD является суммой углов BAC и CAD:

Не забываем, что AD=ВС=12. Остается только подставить все значения в формулу и найти площадь.

Синус угла 60 градусов – табличное значение.

ОТВЕТ: 60√3

Задание №3

В этом задании знаем высоты, но не знаем ни одной стороны. Попробуем найти любую из сторон параллелограмма.

Рассмотрим образовавшийся прямоугольный треугольник ВАЕ:

В этом треугольнике один острый угол равен 60 градусов, значит второй острый угол равен 90-60=30 градусов.

А в прямоугольном треугольнике против угла 30 градусов лежит катет равный половине гипотенузы. Т.е. гипотенуза АВ в два раза больше противолежащего катета ВЕ:

Не забываем что в параллелограмме CD=AB=8. Воспользуемся формулой вычисления площади параллелограмма:

где BF – высота, СD – сторона, к которой проведена высота.

ОТВЕТ: 48

Задание №4

Сторона параллелограмма по сути нам известна (AD=AE+ED=10+4=14).

Попробуем найти высоту.

Для этого сначала посмотрим на образовавшийся выпуклый четырехугольник BEDF, в котором два угла прямые. С учетом, что сумма углов выпуклого четырехугольника равна 360 градусов, можно найти угол FDE (или тот же угол CDA, обозначенный другими буквами ):

Помним, что сумма углов параллелограмма, прилежащих одной стороне, равна 180 градусов. Значит:

Рассмотрим треугольник АВЕ (прямоугольный). Если один его острый угол равен 45 градусов, то второй:

По признаку равнобедренного треугольника получаем, что треугольник АВЕ – равнобедренный с равными сторонами АЕ и ВЕ:

ВЕ, в свою очередь, является высотой параллелограмма АВСD. Значит:

ОТВЕТ: 140

Если вы знаете того, кто готовится к ОГЭ не забудьте поделиться с ним этой информацией. Всегда пригодится.

Продолжение следует…

Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность

(✿◠‿◠)

Всего: 116    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 116    1–20 | 21–40 | 41–60 | 61–80 …

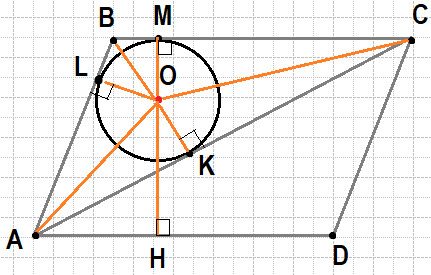
1) Построим па­рал­ле­ло­грам­м (ABCD), про­ве­дём диа­го­наль (AC), построим окружность, впи­сан­ную в тре­уголь­ник (ABC). Рас­сто­я­ния от точки (O) до точки (A) и пря­мых (AD) и (AC) со­от­вет­ствен­но равны 25, 9 и 7.

2) Сделаем дополнительные построения. Центр вписанной окружности — это точка пересечения биссектрис, поэтому (AO), (BO), (CO)  — биссектрисы. Проведём касательные — (OK), (OM), (OL).  Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

3) Из прямоугольного треугольника (AOK) по теореме Пифагора найдём (AK):

AK=AO2−OK2=252−72=625−49=576=24.

5) Площадь треугольника (ABC) можно найти как произведение радиуса вписанной окружности на полупериметр:

SABC=AB+BC+AC2⋅OK=AL+LB+BM+MC+CK+AK2⋅OK;

так как (AL=AK), (BM=LB), (MC=CK), то

SABC=2⋅AL+2BM+2MC2⋅7=2⋅24+2BM+2MC2⋅7=24+BM+MC⋅7.

6) Площадь параллелограмма равна произведению высоты на основание:

SABCD=MH⋅BC=MO+OH⋅BM+MC=16BM+MC.

7) Рассмотрим треугольники (ABC) и (ACD): (AB) равно (CD), (AD) равно (BC), углы (ABC) и (ADC) равны, следовательно, треугольники (ABC) и (ACD) равны. Поэтому площадь треугольника (ABC) равна половине площади параллелограмма:

7⋅24+BM+MC=12⋅16BM+MC⇔BM+MC=168.

8) Площадь параллелограмма равна:

SABCD=MH⋅BC=16⋅168=2688.

Ответ: 2688.

РЕШЕНИЕ ЗАДАНИЙ ОГЭ по теме «ПАРАЛЛЕЛОГРАММ»

Памятка.

Четырехугольник, у которого противоположные стороны параллельны, называется параллелограммом.

Свойства:

• В параллелограмме противоположные стороны равны.

• В параллелограмме противоположные углы равны.

• В параллелограмме сумма углов, прилегающих к одной стороне, равна 180°.

• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

• Диагональ параллелограмма делят его на два равных треугольника.

Признаки:

• Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник параллелограмм.

• Если в четырехугольнике две противоположные стороны параллельны и равны, то этот четырехугольник параллелограмм.

• Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник параллелограмм.

• Если в четырехугольнике противоположные углы попарно равны, то этот четырехугольник параллелограмм.

Свойство диагоналей параллелограмма:

• Диагонали параллелограмма пересекаются и в точке пересечения делятся пополам.

Свойство противоположных сторон и углов параллелограмма:

• У параллелограмма противоположные стороны и углы равны.

Это интересно:

• Если провести биссектрисы двух противоположных углов параллелограмма, то они будут параллельны или совпадут.

• Если провести биссектрисы двух углов, прилегающих к одной стороне параллелограмма, то они будут перпендикулярны.

Площадь параллелограмма.

S = ah, S = 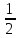d₁d₂sin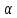, S = absin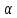, гдеa,b- стороны, 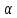– угол между сторонами.

В параллелограмме можно из одного угла провести 2 высоты.

Меньшая высота проведена к большей стороне.

Большая – к меньшей.

Если в четырехугольник вписана окружность, то суммы противоположных сторон равны.

АD + BC = AB + CD

РЕШЕНИЕ ЗАДАЧ.

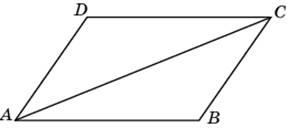
1.Диагональ параллелограмма образует с двумя его сторонами углы 26°  и 34°. Найдите больший угол параллелограмма. Ответ дайте в градусах.

Решение.

А = 26° +34° = 60°
В = 180° – 60 ° = 120°

Ответ. 120

2.Диагональ параллелограмма образует с двумя его сторонами углы 33°  и  11°. Найдите больший угол параллелограмма. Ответ дайте в градусах.

3. Диагональ параллелограмма образует с двумя его сторонами углы 24° и 47° . Найдите больший угол параллелограмма. Ответ дайте в градусах.

4.В параллелограмме ABCD  диагональ АС в 2 раза больше стороны АВ и  ACD = 104°. Найдите острый угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение. Пусть CD = x, тогда и ОС = х, ОС = СD, ОСD– равнобедренный.

СОD = (180 – 104): 2 = 38

5. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=1°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

6. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=166°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

7. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1  и HD = 28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.

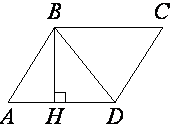
Решение.AD = 1 + 28 = 29. BH = 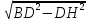= = 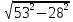= = 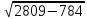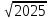45.

S = AH•BH, S = 29•45 = 1305.

8. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.

9. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=8 и HD=40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма.

10. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла Aобразует со стороной BC угол, равный 15°. Ответ дайте в градусах.

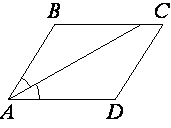
Решение. ВС 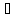АD, то ВСА = САD, а так как АС – биссектриса, то ВАС = САD, то ВСА= ВАС, значит, АВС = равнобедренный. А = 30°.

11. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 33°. Ответ дайте в градусах.

12. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.

13. Найдите площадь параллелограмма, изображённого на рисунке.

14.

15. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма. Ответ дайте в градусах.

16. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.

17. На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

1. 2. 3.

18. Площадь параллелограмма ABCD равна 24. ТочкаE – середина стороны CD. Найдите площадь трапеции ABED.

Решение. Пусть DE = x, тогда АВ = 2х, S_{трапеции} = •h =

S_{паралл.} = CD•h = 2x•h = 24, xh = 12, тогдаS_тр= = 18

19.Площадь параллелограмма  равна 189. Точка  — середина стороны . Найдите площадь трапеции .

20. Площадь параллелограмма  равна 123. Точка  — середина стороны . Найдите площадь трапеции .

ОТВЕТЫ.

№	1	2	3	4	5	6	7	8	9	10
Ответ	120	136	109	38	89,5	7	1305	1024	1440	30
№	11	12	13	14	15	16	17	18	19	20
Ответ	66	82	120	20	105	45	1) 28 2) 10 3) 20	18	141,75	92,25

II часть.

1.Биссектриса угла  параллелограмма  пересекает сторону  в точке . Найдите периметр параллелограмма, если , .

Решение.

АК – биссектриса, поэтомуВАК=КАD, а КАD= ВКА (как накрест лежащие при параллельных прямых), поэтому треугольник ВАК – равнобедренный, ВА=BK=7, а стороны ВС=АD=7+12=19, отсюда P=19+19+7+7=52.

2.Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=5, CK=14. Ответ. 38

Решите самостоятельно:

1. Диагональ параллелограмма образует с двумя его сторонами углы 52°  и 10°. Найдите больший угол параллелограмма. Ответ дайте в градусах.

2. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=173°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

3. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=7 и HD=24. Диагональ параллелограмма BD равна 51. Найдите площадь параллелограмма.

4. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 40°. Ответ дайте в градусах.

5. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.

II часть.

1. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=8, CK=13.

Среди задач на вычисление площади параллелограмма из открытого банка ФИПИ есть и е, на которые достаточно краткого ответа, и с развернутым ответом. И те, и другие, перед вами. Любое из них может вам попасться на экзамене в этом году.

Вспоминаем, что площадь параллелограмма равна произведению длины основания на высоту:
S = ah

Реальные задания по геометрии из банка ФИПИ

Найдите площадь параллелограмма, изображённого на рисунке.

Решение:

Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+7) * 4 = 40

Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.

Ответ: 40

E8FC9F

Найдите площадь параллелограмма, изображённого на рисунке.

Решение:

Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+4) * 4 = 28

Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.

Ответ: 28

5AEBBA

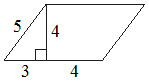
Найдите площадь параллелограмма, изображённого на рисунке.

Решение:

Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+2) * 4 = 20

Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.

Ответ: 20

460490

Найдите площадь параллелограмма, изображённого на рисунке.

Решение:

Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+8) * 4 = 44

Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.

Ответ: 44

29D63A

Найдите площадь параллелограмма, изображённого на рисунке.

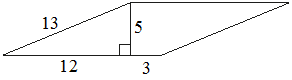
Решение:

Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (12+3) * 5 = 75

Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.

Ответ: 75

D97D85

Найдите площадь параллелограмма, изображённого на рисунке.

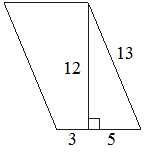
Решение:

Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+5) * 12 = 96

Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.

Ответ: 96

B08979

Найдите площадь параллелограмма, изображённого на рисунке.

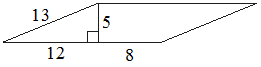
Решение:

Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (12+8) * 5 = 100

Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.

Ответ: 100

956EDE

Найдите площадь параллелограмма, изображённого на рисунке.

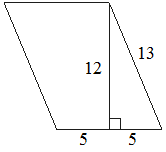
Решение:

Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (5+5) * 12 = 120

Значение длины второй стороны параллелограмма – лишние данные, они не используются в решении.

Ответ: 120

66228A 

Задания второй части ОГЭ с расширенным решением

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.

Решение:

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$sqrt{AO^2+ОК^2}=;sqrt{25-9}$ = 4

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 4.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{4+4+2BM+2MC}2ast3=3ast(4+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(3+4)ast(BM+MC)=7ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$frac{7ast(BM+MC)}2=3;ast;(;4;+;B;M;+;M;C)\7ast(BM+MC);=;6;ast;(;4;+;B;M;+;M;C)\7ast(BM+MC);=;24;+;6;ast;(B;M;+;M;C)\7ast(BM+MC);-;6;ast;(B;M;+;M;C);=;24\B;M;+;M;C;=;24\\\$

 То есть основание BC = 24.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(3+4)*24=168

Ответ:  168

701E1F

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 6 и 5. Найдите площадь параллелограмма ABCD.

Решение:

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$sqrt{AO^2+ОК^2}=;sqrt{169-25}$ = 12

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{12+12+2BM+2MC}2ast5=5ast(12+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(6+5)ast(BM+MC)=11ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$frac{11ast(BM+MC)}2=5ast(12+BM+MC)\11ast(BM+MC);=;10ast(12+BM+MC)\11ast(BM+MC);=;120;+;10ast(BM+MC)\11ast(BM+MC);-;10;(BM+MC);=;120\B;M+M;C;=;120\\\$

 То есть основание BC = 120.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+6)*120=1320

Ответ:  1320

B520E8

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 7 и 5. Найдите площадь параллелограмма ABCD.

Решение:

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$sqrt{AO^2+ОК^2}=;sqrt{169-25}$ = 12

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{12+12+2BM+2MC}2ast5=5ast(12+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(7+5)ast(BM+MC)=12ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$frac{12ast(BM+MC)}2=5ast(12+BM+MC)\12ast(BM+MC);=;10ast(12+BM+MC)\12ast(BM+MC);=;120;+;10ast(BM+MC)\12ast(BM+MC);-;10;(BM+MC);=;120\2ast(BM+MC);=;120\BM+MC;=;60\\\\$

 То есть основание BC = 60.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(7+5)*60=720

Ответ:  720

7AFAA8

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 8 и 5. Найдите площадь параллелограмма ABCD.

Решение:

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$sqrt{AO^2+ОК^2}=;sqrt{169-25}$ = 12

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{12+12+2BM+2MC}2ast5=5ast(12+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(8+5)ast(BM+MC)=13ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$frac{13ast(BM+MC)}2=5ast(12+BM+MC)\13ast(BM+MC);=;10ast(12+BM+MC)\13ast(BM+MC);=;120;+;10ast(BM+MC)\13ast(BM+MC);-;10;(BM+MC);=;120\3ast(BM+MC);=;120\BM+MC;=;40\\\\$

 То есть основание BC = 40.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+8)*40=520

Ответ:  520

15838B

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.

Решение:

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$sqrt{AO^2+ОК^2}=;sqrt{169-25}$ = 12

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{12+12+2BM+2MC}2ast5=5ast(12+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(9+5)ast(BM+MC)=14ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$frac{14ast(BM+MC)}2=5ast(12+BM+MC)\14ast(BM+MC);=;10ast(12+BM+MC)\14ast(BM+MC);=;120;+;10ast(BM+MC)\14ast(BM+MC);-;10;(BM+MC);=;120\4ast(BM+MC);=;120\BM+MC;=;30\\\\$

 То есть основание BC = 30.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+9)*30=420

Ответ:  420

221DAD

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.

Решение:

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$sqrt{AO^2+ОК^2}=;sqrt{625-49}$ = 24

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{24+24+2BM+2MC}2ast7=7ast(24+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(13+7)ast(BM+MC)=20ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$frac{20ast(BM+MC)}2=7ast(24+BM+MC)\20ast(BM+MC);=;14ast(24+BM+MC)\20ast(BM+MC);=;336;+;14ast(BM+MC)\20ast(BM+MC);-;14;(BM+MC);=;336\6ast(BM+MC);=;336\BM+MC;=;56\\\\$

 То есть основание BC = 56.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(13+7)*56=1120

Ответ:  1120

716CE8

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 14 и 7. Найдите площадь параллелограмма ABCD.

Решение:

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$sqrt{AO^2+ОК^2}=;sqrt{625-49}$ = 24

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{24+24+2BM+2MC}2ast7=7ast(24+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(14+7)ast(BM+MC)=21ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$frac{21ast(BM+MC)}2=7ast(24+BM+MC)\21ast(BM+MC);=;14ast(24+BM+MC)\21ast(BM+MC);=;336;+;14ast(BM+MC)\21ast(BM+MC);-;14;(BM+MC);=;336\7ast(BM+MC);=;336\BM+MC;=;48\\\\$

 То есть основание BC = 48.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(14+7)*48=1008

Ответ:  1008

A4192E

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 15 и 7. Найдите площадь параллелограмма ABCD.

Решение:

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$sqrt{AO^2+ОК^2}=;sqrt{625-49}$ = 24

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{24+24+2BM+2MC}2ast7=7ast(24+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(15+7)ast(BM+MC)=22ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$frac{22ast(BM+MC)}2=7ast(24+BM+MC)\22ast(BM+MC);=;14ast(24+BM+MC)\22ast(BM+MC);=;336;+;14ast(BM+MC)\22ast(BM+MC);-;14;(BM+MC);=;336\8ast(BM+MC);=;336\BM+MC;=;42\\\\$

 То есть основание BC = 42.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(15+7)*42=924

Ответ:  924

2E555E

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 17 и 7. Найдите площадь параллелограмма ABCD.

Решение:

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$sqrt{AO^2+ОК^2}=;sqrt{625-49}$ = 24

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{24+24+2BM+2MC}2ast7=7ast(24+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(17+7)ast(BM+MC)=24ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$frac{24ast(BM+MC)}2=7ast(24+BM+MC)\24ast(BM+MC);=;14ast(24+BM+MC)\24ast(BM+MC);=;336;+;14ast(BM+MC)\24ast(BM+MC);-;14;(BM+MC);=;336\10ast(BM+MC);=;336\BM+MC;=;33,6\\\\$

 То есть основание BC = 33,6.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(17+7)*33,6=806,4

Ответ:  806,4

DFC86B

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 19 и 7. Найдите площадь параллелограмма ABCD.

Решение:

 Сделаем построения и введём обозначения, как показано на рисунке. O  — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности  — это точка пересечения биссектрис, поэтому AO,BO,CO  — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:

AK=$sqrt{AO^2+ОК^2}=;sqrt{625-49}$ = 24

Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству касательных, а углы LAO и OAK равны, так как АО биссектриса. AO  — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
 Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
 Аналогично из равенства треугольников BOL и BOM  — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

$Sabc=frac{AB+BC+CA}2ast OK=frac{AL+LB+BM+MC+CK+KA}2ast OK=frac{24+24+2BM+2MC}2ast7=7ast(24+BM+MC)$

* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:

$Sabcd=MHast BC=(MO+OH)ast(BM+MC)=(19+7)ast(BM+MC)=26ast(BM+MC)$

Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:

$frac{26ast(BM+MC)}2=7ast(24+BM+MC)\26ast(BM+MC);=;14ast(24+BM+MC)\26ast(BM+MC);=;336;+;14ast(BM+MC)\26ast(BM+MC);-;14;(BM+MC);=;336\12ast(BM+MC);=;336\BM+MC;=28\\\\$

 То есть основание BC = 28.

Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(19+7)*28=728

Ответ:  728

1D6569

---

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.

Решение:

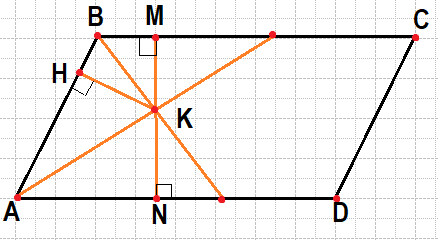
Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=7.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=7. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =19*(7+7)=19*14=266.

Ответ: 266

97C87B

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.

Решение:

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=3.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=3. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =11*(3+3)=11*6=66.

Ответ: 66

F8A0E6

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.

Решение:

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=9.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=9. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =12*(9+9)=12*18=216.

Ответ: 216

67503F

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 10.

Решение:

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=10.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=10. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =19*(10+10)=19*20=380.

Ответ: 380

D60F99

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=17, а расстояние от точки K до стороны AB равно 10.

Решение:

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=10.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=10. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =17*(10+10)=17*20=340.

Ответ: 340.

B435D4

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=18, а расстояние от точки K до стороны AB равно 1.

Решение:

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=1.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=1. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =18*(1+1)=18*2=36.

Ответ: 36

E097F7

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=7, а расстояние от точки K до стороны AB равно 4.

Решение:

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=4.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=4. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =7*(4+4)=7*8=56.

Ответ: 56

80A169

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 8.

Решение:

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=8.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=8. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =2*(8+8)=2*16=32.

Ответ: 32

569075

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=6, а расстояние от точки K до стороны AB равно 6.

Решение:

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=6.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=6. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =6*(6+6)=6*12=72.

Ответ: 72

FD6657

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 1.

Решение:

Введём обозначения, как показано на рисунке. Пусть К  — точка пересечения биссектрис, КН  — высота треугольника АКВ, MN  — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК  — биссектриса угла А.  Во-вторых, сторона AK  — общая. Тогда KN=KH=1.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=1. 
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.

Итак, площадь параллелограмма это произведение высоты на основание:

S=AD*MN=AD*(MK + KN) =2*(1+1)=2*2=4.

Ответ: 4

A7594E