В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)
Формула получена следующим образом:
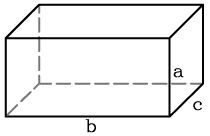
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.
Как найти площадь поверхности параллелепипеда
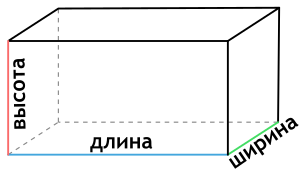
На данной странице калькулятор поможет рассчитать площадь поверхности параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
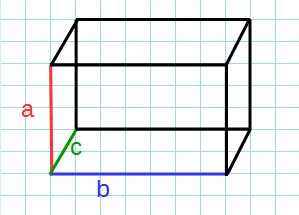
a:
b:
c:
Результат
Ответы:
Формула площади поверхности параллелепипеда через его ребра:
a, b, c – ребра параллелепипеда.
Параллелепипед – это призма, в основании которой находится параллелограмм. Противоположные стороны параллелепипеда равны. Соответственно, у них будут и равные площади. Всего у параллелепипеда 6 граней, значит:
Sобщ = 2(S1+S2+S3)
Идем дальше. Примем, что ребра параллелограмма равны a, b и с. Где a, b – стороны основания (образуют S1), а с – высота параллелограмма. b и с образуют S2, а c и a образуют S3.
Далее: существует несколько различных случаев:
1) Если все шесть граней параллелепипеда являются прямоугольниками – то такой параллелепипед называется прямоугольным. И его площадь высчитывается по формуле:
Sобщ = 2(S1+S2+S3) = 2(ab + bс + aс)
2) Если четыре из шести граней параллелограмма являются прямоугольниками, то такой параллелепипед называется прямым. Его площадь считается не только через длину его ребер, но и через величину непрямого угла между сторонами параллелограмма, не являющегося прямоугольником:
Sобщ = 2(S1+S2+S3) = 2(absinX + сb + aс)
3) Куб – тоже частный случай параллелограмма. Это прямоугольный параллелограмм, все ребра которого равны. Соответственно, будут равны и все стороны. Площадь высчитывать легче всего:
Sобщ = 2(S1+S2+S3) = 2(a^a+а^2+a^2)=6a^2, где а – ребро куба.
Общая формула площади поверхности параллелограмма в полном варианте применяется в тех случаях, когда он не является прямоугольным. Ребра такой призмы расположены не под прямым углом друг к другу, а значит синус этих углов не равен единице, как в предыдущих случаях, когда мы его просто не указывали.
Если допустить, что углы между ребрами параллелограмма равны:
- угол между а и b = X
- угол между а и c = Y
- угол между c и b = Z
Тогда:
Sобщ = 2(S1+S2+S3) = 2(absinX + сbsinZ + aсsinY)
Далее можно упомянуть еще один вид параллелограммов: те, у которых лишь две стороны являются прямоугольниками. Допустим, что S1 – это площадь прямоугольника в основании. Тогда:
Sобщ = 2(S1+S2+S3) = 2(absinX + сbsinZ + aсsinY) = 2(ab + сbsinZ + aсsinY), т.к. Х=90 градусов и sinX=1.
Вот как-то так)
Площадь параллелепипеда
Параллелепипед – это призма, у основания которой находится параллелограмм. Эта геометрическая фигура обладает шестью гранями, которые представляют собой небольшие параллелограммы. Прямой параллелепипед это параллелепипед, у которого четыре грани представлены в виде прямоугольников, прямоугольный параллелепипед – это такой параллелепипед, у которого все шесть граней выполнены в виде прямоугольников.
Высоту параллелепипеда принято обозначать латинской буквой «h», а ребра «a», «b», «c». Если вам необходимо узнать площадь прямоугольного параллелепипеда, то вы можете это сделать при помощи нашего онлайн калькулятора, который позволит вам за считанные секунды получить верный ответ.
Наш онлайн калькулятор рассчитывает площадь прямоугольного параллелепипеда по формуле: S = 2(ab + bc + ac).
Будьте осторожны и не путайте прямой параллелепипед с прямоугольным.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»


{S_{полн} = 2(ab+bc+ac)}
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер – это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота – это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда
{S_{полн} = 2(ab+bc+ac)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда
{S_{бок} = 2(ac+bc)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .