Лучший ответ
Aljebro
Просветленный
(27044)
11 лет назад
Никак, т. к. 4 сторон (разных, правда, всего 2) недостаточно. Максимальная будет у прямоугольника, минимальную можно устремить к 0.
Остальные ответы
Алекс Сазонов
Профи
(536)
11 лет назад
Этих данных будет недостаточно. нужен угол меду сторонами.
Квантор
Просветленный
(34142)
11 лет назад
площадь вписанного четырехугольника находится по формуле:
Если же четырехугольник и вписанный, и описанный одновременно, его площадь находится по более простой формуле:

{S = a cdot h}
Найти площадь параллелограмма
На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные – основание, высоту, стороны, диагонали и углы между ними и получите ответ.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Содержание:
- калькулятор площади параллелограмма
- формула площади параллелограмма через сторону и высоту
- формула площади параллелограмма через две стороны и угол между ними
- формула площади параллелограмма через диагонали и угол между ними
- примеры задач
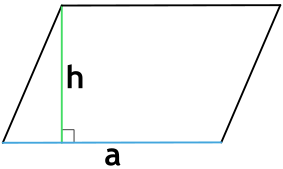
Формула площади параллелограмма через сторону и высоту
{S = a cdot h}
a – сторона параллелограмма
h – высота параллелограмма
Формула площади параллелограмма через две стороны и угол между ними
{S=a cdot b cdot sin(alpha)}
a, b – стороны параллелограмма
α – угол между сторонами a и b
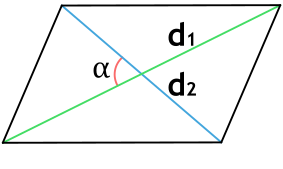
Формула площади параллелограмма через диагонали и угол между ними
{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}
d1, d2 – диагонали параллелограмма
α – угол между диагоналями
Примеры задач на нахождение площади параллелограмма
Задача 1
Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.
Решение
Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.
S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Мы можем проверить ответ с помощью калькулятора .
Задача 2
Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.
Решение
Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.
S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2
Ответ: 48 см²
И снова проверить ответ нам поможет калькулятор .
Задача 3
Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.
Решение
В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.
S = a cdot h = 12 cdot 8 = 96 : см^2
Ответ: 96 см²
И снова проверить ответ нам поможет калькулятор .
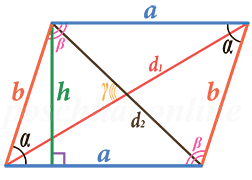
1. Формула площади параллелограмма через стороны и углы
a, b – стороны параллелограмма
α, β – углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):
Калькулятор – вычислить, найти площадь параллелограмма:
a(сторона)=
b(сторона)=
α или β (угол в градусах)= ( sin α=sin β )
S=
2. Формула площади параллелограмма через сторону и высоту
a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D – большая диагональ
d –меньшая диагональ
α, β – углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
Калькулятор – вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
Как найти площадь параллелограмма
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти площадь параллелограмма
Чтобы найти площадь параллелограмма воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны друг другу.
Узнать чему равна площадь параллелограмма (S) можно зная (либо-либо):
- длину стороны a и длину высоты h
- длины сторон a и b, и угол α
- длины сторон a и b, и угол β
- длины сторон a и b, и длину любой из диагоналей (d1 или d2)
- длины диагоналей d1 и d2, и угол между ними γ
Подставьте значения в соответствующие поля и получите результат.
Зная длину стороны a и длину высоты h
Чему равна площадь параллелограмма если сторона
a = ,
а высота
h = ?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длина стороны a и длина высоты h, проведенной к этой стороне?
Формула
S = a⋅h
Пример
Если сторона параллелограмма a = 8 см, а высота h = 4 см, то:
S = 8 ⋅ 4 = 32 см2
Зная длины сторон a и b, и угол α
Чему равна площадь параллелограмма если сторона
a = ,
сторона
b = ,
а угол между ними
α = °
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними α?
Формула
S = a⋅b⋅sinα
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠α = 50° то:
S = 8 ⋅ 5 ⋅ sin 50 = 40 ⋅ 0.766 ≈ 30.64 см2
Зная длины сторон a и b, и угол β
Чему равна площадь параллелограмма если сторона
a = ,
сторона
b = ,
а угол между ними
β = °
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними β?
Формула
S = a⋅b⋅sin(180 – β)
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠β = 130° то:
S = 8 ⋅ 5 ⋅ sin(180-130) = 40 ⋅ 0.766 ≈ 30.64 см2
Зная длины сторон a и b, и длину диагонали (d1 или d2)
Чему равна площадь параллелограмма если сторона
a = ,
сторона
b = ,
а диагональ
d =
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины сторон a и b, и длина любой из диагоналей d?
Формула
S = 2√p⋅(p-a)⋅(p-b)⋅(p-d), где p=(a+b+d)/2
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а диагональ d = 11 см то:
p = (8 + 5 +11)/2 = 12
S = 2√12⋅(12-8)⋅(12-5)⋅(12-11) = 2⋅√12⋅4⋅7⋅1 = 2⋅√336 = 36.66 см2
Зная длины диагоналей d1 и d2, и угол между ними γ
Чему равна площадь параллелограмма если диагональ
d1 = ,
диагональ
d2 = ,
а угол между ними
γ = °
?
Ответ: S =
0
Чему равна площадь параллелограмма S если известны длины диагоналей d1 и d2, и угол между ними γ?
Формула
S = ½⋅d1⋅d2⋅sinγ
Пример
Если диагональ параллелограмма d1 = 11 см, диагональ d2 = 7 см, а ∠γ = 45° то:
S = ½ ⋅ 11 ⋅ 7 ⋅ sin 45 = 38.5 ⋅ 0.7071 ≈ 27.22 см2
См. также
Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.
-
Формула вычисления площади
-
По длине стороны и высоте
- По двум сторонам и углу между ними
- По двум диагоналям и углу между ними
-
По длине стороны и высоте
- Примеры задач
Формула вычисления площади
По длине стороны и высоте
Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h
По двум сторонам и углу между ними
Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:
S = a ⋅ b ⋅ sin α
По двум диагоналям и углу между ними
Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:
S = 1/2 ⋅ d 1 ⋅ d 2 ⋅ sin α
Примеры задач
Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.
Решение:
Используем первую формулу, в которой задействованы известные нам по условиям задания значения: S = 4 см * 7 см = 28 см2.
Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.
Решение:
Применим вторую формулу, рассмотренную выше: S = 6 см * 8 см * sin 30° = 24 см2.
Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.
Решение:
Воспользуемся формулой, в которой фигурируют диагонали: S = 1/2 * 4 см * 6 см * sin 90° = 12 см2.