Как найти площадь параллелограмма по его координатам

Вспомним в начале, что такое векторное произведение.

Если для векторов присутствуют некоторые координаты ($vec{a}={x_1; y_1; z_1}$ и $vec{b}= {x_2; y_2; z_2}$), то их векторное произведение в декартовой системе координат можно определить по формуле:

$[a times b] = {y_1 cdot z_2 – y_2 cdot z_1; z_1 cdot x_2 – z_2 cdot x_1; x_2 cdot y_2 – x_2 cdot y_1}$

Легче всего запомнить эту формулу записав в форме определителя:

$[ab] = begin{array} {|ccc|} i & j & k \ x_1 & y_1 & z_1 \ x_2 & y_2 & z_2 \ end{array}$.

Эта формула весьма удобна для использования, но чтобы понимать, как её использовать, для начала следует ознакомиться с темой матриц и их определителей.

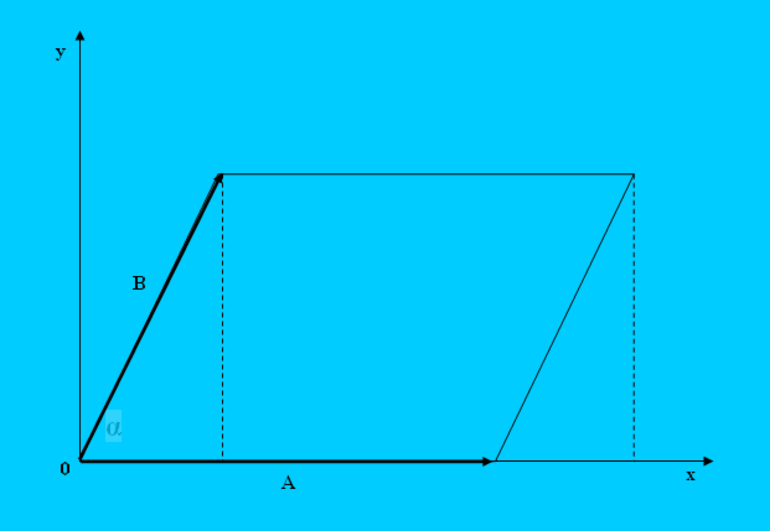
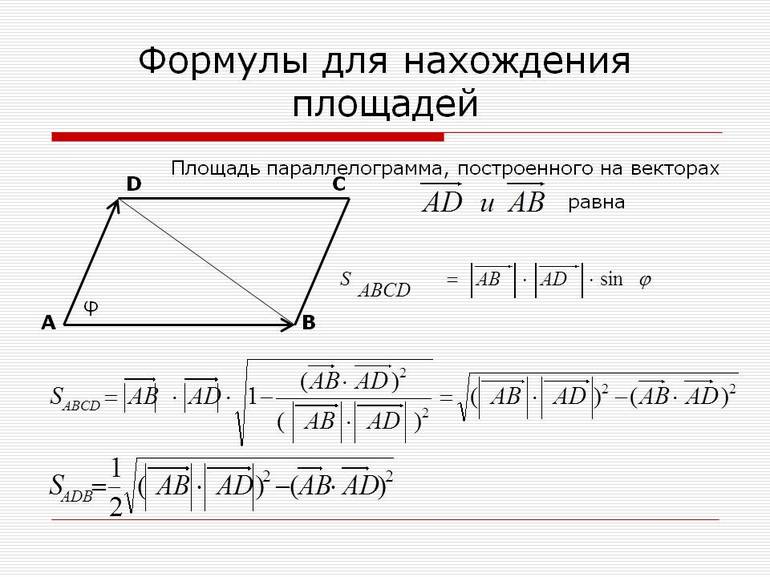
Площадь параллелограмма, стороны которого определяются двумя векторами $vec{a}$ и $vec{b}$ равна скаляру векторного произведения данных двух векторов.

Это соотношение совсем несложно вывести.

Вспомним формулу для нахождения площади обычного параллелограмма, который можно охарактеризовать образующими его отрезками $a$ и $b$:

$S = a cdot b cdot sin α$

При этом длины сторон равны скалярным значениям векторов $vec{a}$ и $vec{b}$, что вполне себе подходит нам, то есть, скаляр векторного произведения данных векторов и будет площадью рассматриваемой фигуры.

«Примеры как вычислить площадь параллелограмма, построенного на векторах» 👇

Данный ход рассуждений справедлив не только для нахождения площади в 3-хмерном пространстве, но и для двухмерного. Познакомьтесь со следующей задачкой на эту тему.

Предыдущие задачи были о векторах, координаты которых заданы в декартовой системе координат, но рассмотрим также случай, если угол между базисными векторами отличается от $90°$:

Четырехугольник и вектор на плоскости

Каждый школьник понимает, что параллелограмм является специальным видом плоских четырехугольников. Эта фигура состоит из двух пар параллельных пересекающихся отрезков. Она обладает следующими важными свойствами:

• ее противоположные стороны и углы равны друг другу;
• сумма всех четырех углов составляет 360 градусов;
• если просуммировать лишь два смежных (прилежащих к одной стороне) угла, то получится значение 180 градусов;
• любая диагональ делит фигуру на две равные части (треугольники);
• пересечение диагоналей происходит в точке, которая является геометрическим и массовым центром параллелограмма;
• любая секущая, которая проходит через геометрический центр, делит фигуру на две равные по площади части.

Специальные типы

Исходя из определения параллелограмма, как четырехугольника с параллельными и равными по длине противоположными сторонами, можно привести несколько видов фигуры, которые обладают высокой симметрией по отношению к ряду элементарных операций. Это следующие геометрические типы:

1. Квадрат. Все четыре стороны его равны по длине между собой, а углы составляют 90 градусов. Он является фигурой с достаточно высокой симметрией, и его площадь вычисляется просто как квадрат длины любой его стороны.
2. Прямоугольник. Еще один вид параллелограмма, все углы которого являются прямыми. Его симметрия несколько ниже, чем у квадрата, поскольку длины сторон равны лишь попарно. Площадь фигуры можно вычислить, перемножив длины смежных сторон.
3. Ромб. Специальный геометрический тип параллелограмма, который характеризуется тем, что длины всех его сторон являются одинаковыми. Углы фигуры попарно равны и отличаются от 90 градусов (два тупых и два острых).

Направленные отрезки и операция умножения

Площадь параллелограмма через векторы рассчитать легко, если знать понятие направленного отрезка и уметь работать с соответствующими математическими операциями. Поскольку любая точка на плоскости может быть представлена в виде набора двух координат в декартовой прямоугольной системе, то для P и Q можно записать:

P (x1, y1); Q (x2, y2).

Где числа x1, y1, x2 и y2 являются соответствующими координатами для точек P и Q по осям абсцисс и ординат. Чтобы получить вектор PQ-, который будет направлен из P в точку Q, необходимо из координат Q попарно вычесть значения для P:

PQ- = Q — P = (x2-x1, y2-y1).

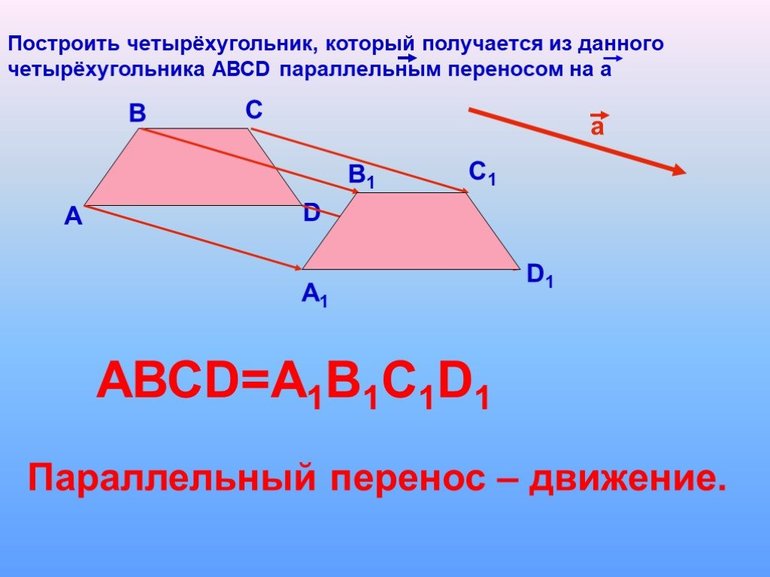
Координаты направленного отрезка на плоскости определяются так же, как и для точки, набором из двух чисел. Чтобы построить такой вектор в системе координат, необходимо его начало расположить в точке (0, 0), а конец со стрелкой будет располагаться в точке (x2-x1, y2-y1). Из этой геометрической интерпретации следует, что существует бесконечное множество направленных отрезков, которые эквивалентны между собой. Получаются они друг из друга с помощью параллельного переноса по всей плоскости координат.

Как и числа, направленные отрезки также можно складывать между собой, вычитать и умножать. Рассматривая вопрос построение параллелограмма на векторах и нахождения его площади, необходимо изучить свойства векторного произведения. Оно представляет собой вектор, перпендикулярный плоскости, в которой лежат исходные направленные отрезки. Пусть a- и b- необходимо умножить векторно. Результатом произведения будет следующий вектор c-:

c- = [a-*b-] = |a-|*|b-|*sin (alfa).

Здесь alfa — угол между a- и b-, а |a-| и |b-| – длины соответствующих направленных отрезков.

Направление c- принято определять с помощью правила правой руки. Оно гласит: если четыре пальца ладони направить от конца первого умножаемого вектора к концу второго, то оттопыренный большой палец укажет направление результирующего векторного умножения.

Координаты вектора c- можно вычислить также, если воспользоваться понятием определителя матрицы. Пусть a- имеет координаты (a1, a2), а b- = (b1, b2), тогда формула для определения c- запишется в следующем виде:

c- = (0, 0, (a1*b2-b1*a2)).

Вектор c- имеет первые две нулевые координаты, поскольку он перпендикулярен плоскости, в которой находятся a- и b-.

Формула площади из геометрии

Чтобы получить формулу площади параллелограмма на векторах, необходимо вспомнить, как рассчитывается эта величина для треугольника. Если известна одна сторона (основание a) и высота, которая на нее опущена (h), то получается простое выражение:

S3 = ½*h*a.

Где S3 — площадь треугольника. Поскольку две таких плоских фигуры, которые соединены одной из своих сторон, образуют четырехугольник-паралелограм, то для него рассмотренную величину можно вычислить по формуле:

S4 = 2*S3 = h*a.

Пусть вторая сторона параллелограмма равна b, тогда с высотой h она связана через определение тригонометрической функции синус:

sin (alfa) = h/b => h = b*sin (alfa).

Если подставить это равенство в выражение для S4, то нахождение площади фигуры сведется к расчету произведения двух его смежных сторон и синуса угла между ними:

S4 = a*b*sin (alfa).

Поскольку угол alfa изменяется от 0 до 180 градусов, то функция синус всегда имеет положительное значение. Этой формулой часто пользуются на практике. Распространение инженерных калькуляторов позволяет быстро и с высокой точностью вычислять синусы любых углов.

Построение параллелограмма

Определить площадь четырехугольника с попарно параллельными сторонами можно не только через длины его сторон. Если внимательно посмотреть на формулу для S4, то можно заметить, что она идентична по виду векторному произведению направленных отрезков.

Пусть имеется два вектора a- и b-. Угол между ними равен alfa. Если их начала совместить в одной точке на плоскости, затем, от конца a- продолжить вектор b-, а из b- начертить a-, то получится параллелограмм, побудованый на a- и b-. Очевидно, что модуль векторного произведения этих направленных отрезков будет равен площади полученной фигуры:

S4 = a*b*sin (alfa) = |[a-*b-]|.

Применяя координатное выражение этого произведения, можно записать следующую формулу для площади:

S4 = |(a1*b2-b1*a2)|.

Где a- = (a1,a2) и b-=(b1,b2). Знак модуля необходим потому, что по правилу правой руки могут получаться отрицательные векторы. Площадь же является всегда величиной положительной.

Преимущество последней записанной формулы для S4 по сравнению с выражением, где необходимо знать длины и углы, заключается в том, что ее использование не требует никаких предварительных вычислений. Достаточно лишь знать координаты конца и начала образующих параллелограмм векторов.

Задача с тремя точками

Чтобы научиться пользоваться записанной простой формулой, следует решить простую задачу. Имеется три точки, координаты которых следующие:

• A (1,-1);
• B (2, 0);
• C (-4, 3).

На вершинах этих точек следует построить параллелограмм, а затем, рассчитать его площадь S4.

Задачу проще всего решать через использование векторов. Выберем произвольную точку из трех заданных. Пусть это будет A. Из нее выходит два вектора: AB- и AC-. Их координаты определяются таким образом:

AB- = (2−1, 0-(-1)) = (1, 1); AC- = (-4−1, 3- (-1)) = (-5, 4).

Чтобы определить площадь параллелограмма на этих векторах, следует применить формулу для их векторного произведения. Порядок умножения направленных отрезков не имеет значения. Получается следующий результат:

S4 = [AB-*AC-] = 1*4 — (-5)*1 = 9.

Результат получен в единицах квадратных соответствующей двумерной системы координат.

Если была выбрана в качестве исходной не точка A, а B или C, то получился бы тот же результат, что можно доказать, проделав аналогичные вычисления.

Диагонали фигуры

Некоторые задачи по геометрии параллелограммов в качестве начального условия предлагают знание одной или двух его диагоналей. По этим данным необходимо вычислить характеристики всей фигуры, включая ее площадь. Решать такие задачи также удобно с использованием понятия векторов.

Если дана диагональ, выраженная вектором f- и основание, представленное направленным отрезком a-, то формула для площади параллелограмма имеет вид:

S4 = [a-*f-] = |a-|*|f-|*sin (beta).

Где beta — угол между a- и f-. Видно, что это выражение не отличается от предыдущих для S4. Доказать его справедливость несложно, если рассмотреть построенные на указанных векторах треугольники и использовать признаки их подобия.

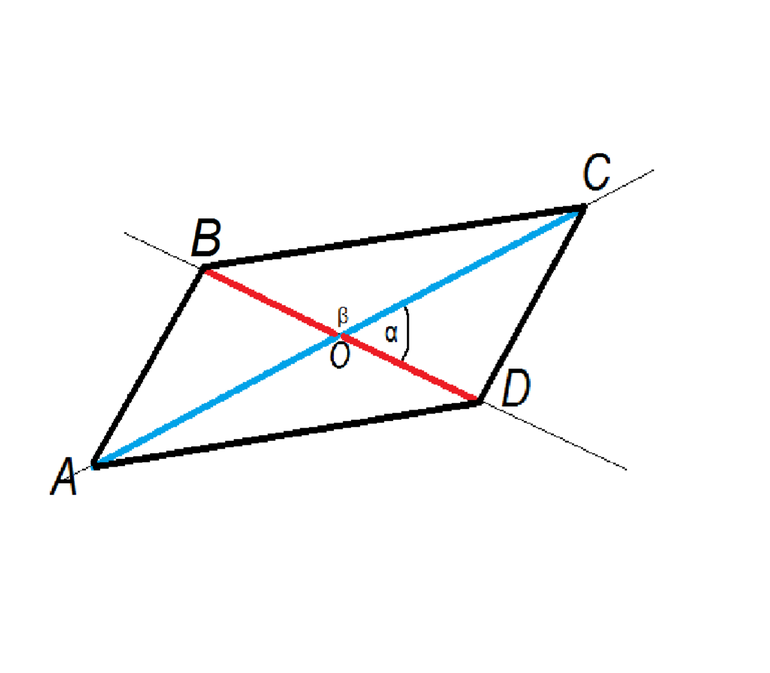
Другой случай, когда даны обе диагонали параллелограмма f- и e-. Воспользовавшись геометрическими построениями на плоскать, можно показать справедливость следующего выражения:

S4 = ½*|[e-*f-]| = ½*|e-|*|f-|*sin (teta).

Здесь teta — это угол пересечения e- и f-. Таким образом, чтобы вычислить площадь параллелограмма, диагоналями которого служат вектора, следует вычислить половину модуля их векторного произведения.

Пример решения

Все разнообразие задач на определение площади параллелограмма сводится к знанию единственной формулы векторного произведения. Пусть известны две диагонали фигуры. Они имеют координаты:

e- = (2, -1); f- = (1, -4).

Чтобы определить величину S4, достаточно без промежуточных вычислений воспользоваться формулой векторного произведения заданных направленных отрезков:

S4 = ½*|[e-*f-]| = ½*|-8+1| = 3,5.

В связи с развитием интернета, всегда можно использовать калькулятор-онлайн для расчета величины S4. Соответствующий электронный ресурс можно знайти, воспользовавшись любой поисковой системой в браузере.

Трехмерное пространство

В пространственной системе координат каждый вектор задается тремя числами, поэтому их векторное произведение c- также будет представлять набор трех цифр. Построенный в пространстве параллелограмм на двух векторах будет иметь площадь, равную длине направленного отрезка c-. Для расчета его модуля следует использовать известное выражение: сумма квадратов трех координат под корнем.

Таким образом, площадь параллелограмма проще всего вычислять, используя операцию умножения векторов. Этот метод является универсальным не только для задач на плоскости, но и для решения проблем в трехмерной системе координат.

Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.

Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье площадь параллелограмма. Площадь будет равняться произведению модулей на синус угла между ними:

Рассмотрим пример расчета площади параллелограмма построенного на векторах.

Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.

Расчет длин сторон фигуры, заданной координатами

Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a(x1;y1;z1), а вектора b(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:


Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.

Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.

Как определить площадь параллелограмма, построенного на векторах

Если по условию задачи даны длины этих векторов, то вычисление площади параллелограмм не вызывает затруднений. Для этого необходимо воспользоваться формулой:

( S=left|aright|timesleft|bright|timessinbeta)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Что такое модуль векторного произведения

Векторным произведением некоторых векторов m и n является третий вектор p.

(overline p;=left|overline mright|timesleft|overline nright|\)

(left|pright|=left|mright|timesleft|nright|timessinalpha\)

Все три эти вектора образуют правую тройку. Это значит, что если привести их к общему началу из конца третьего вектора (р), то кратчайший поворот от первого вектора (m) ко второму вектору (n) будет совершаться против часовой стрелки.

Допустим, вектора заданы координатами:

(overline m=left{x_1;y_1;z_1right}\)

(overline n=left{x_2;y_2;z_2right}\)

В декартовой системе координат их произведение можно будет вычислить по формуле:

(left[mtimes nright]=left{y_1times z_2-y_2times z_1;ztimes x_2-z_2times x_1;x_2times y_2-x_2times y_1right}\)

(left[mtimes nright]=begin{vmatrix}i&j&k\x_1&y_1&z_1\x_2&y_2&z_2end{vmatrix}\\\)

Как рассчитать площадь обычного параллелограмма

Пример

Рассмотрим еще один пример. Дан параллелограмм с длиной сторон a – 5 см, b – 6 см и углом между ними равным 30^0\\\. Необходимо найти его площадь.

Для решения необходимо заменить длины сторон векторными значениями a и b. После этого воспользуемся формулой определения площади параллелограмма, построенного на векторах.

(S=left|5right|timesleft|6right|timessin30^0=30timesfrac12=15\\\)

Таким образом, площадь данного параллелограмма равна 15 квадратным сантиметрам.

Пример решения задачи в трехмерном пространстве

Пример

Даны два вектора, а и b, имеющие в декартовой системе следующие координаты:

(left{4,;2,;6right}\\\)

(left{4,;8,;11right}\\\)

Требуется найти площадь, образуемого ими параллелограмма.

Для решения требуется найти векторное произведение заданных векторов:

(left[atimes bright]=begin{vmatrix}i&j&k\4&2&6\4&8&11end{vmatrix}=ibegin{vmatrix}2&6\8&11end{vmatrix}-jbegin{vmatrix}4&6\4&11end{vmatrix}+kbegin{vmatrix}4&2\4&8end{vmatrix}=ileft(2times11-48right)-jleft(44-24right)+kleft(32-8right)=-26i-20j+24k=left{-26;-20;24right}\\\)

Для полученного отрезка, имеющего направление, найдем модульное значение. Оно и будет площадью параллелограмма, построенного на векторах а и b.

(S=sqrt{left|26right|^2}+sqrt{left|20right|^2}+sqrt{left|24right|^2}=sqrt{676+400+576}=sqrt{1652}\\\)

После извлечения квадратного корня получаем, что площадь параллелограмма равна 40,64.

Пример решения в двухмерном пространстве

Пример

Вычислить площадь параллелограмма, заданного векторами a и b. Их координаты:

(left{4;;5right}\\\)

(left{-7;;8right}\\\)

Оба эти вектора лежат в одной плоскости. Поэтому третью их координату принимаем за 0. Тогда площадь данного параллелограмма будет равна:

(S=sqrt{32+35}=sqrt{67}approx8.2\\\)

Площадь параллелограмма, построенного на векторах

Чтобы найти площадь параллелограмма, построенного на векторах нужно вычислить модуль векторного произведения этих векторов.

Пусть заданы два вектора $ overline{a} = alpha_1 overline{p} + alpha_2 overline{q} $ и $ overline{b} = beta_1 overline{p} + beta_2 overline{q} $, синус угла между ними $ sin varphi $ и длины векторов $ |overline{p}|, |overline{q}| $. Тогда формула записывается следующим образом:

$$ S = Big | [overline{a}, overline{b}] Big | = |alpha_1 beta_2 – alpha_2 beta_1| cdot |overline{p}| cdot |overline{q}| cdot sin varphi $$

Примеры решений

Пример 1

Вычислить площадь параллелограмма, построенного на векторах: $ overline{a} = overline{p}+3overline{q} $ и $ overline{b} = 2overline{p} – overline{q} $, длины которых равны $ |overline{p}|=2, |overline{q}| = 1 $, а угол между ними $ varphi = frac{pi}{6} $

Решение

Вычисляем векторное произведение векторов: $$ [overline{a},overline{b}] = [overline{p}+3overline{q}, 2overline{p}-overline{q}] = $$ Выполняем поэлементное перемножение каждого из слагаемых: $$ = 2[overline{p},overline{p}] – [overline{p},overline{q}] + 6 [overline{q},overline{p}] – 3[overline{q}, overline{q}] = $$ Учитывая свойства векторного произведения, такие как $ [overline{p},overline{p}]=0, [overline{q},overline{q}]=0 $, $ [overline{q},overline{p}]=-[overline{p},overline{q}] $ выполняем упрощение последнего полученного выражения: $$ = 2 cdot 0 – [overline{p},overline{q}] – 6 [overline{p},overline{q}] – 3 cdot 0 = -7 [overline{p},overline{q}] $$ Находим модуль полученного векторного произведения, подставляя из условия задания длины векторов и угол между ними: $$ S = |-7 [overline{p},overline{q}] | = 7 |overline{p}| |overline{q}| sin frac{pi}{6} = 7 cdot 2 cdot 1 cdot frac{1}{2} = 7 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ S = 7 $$

Пример 2

Найти площадь параллелограмма, построенного на векторах: $ overline{a} = overline{p}+overline{q} $ и $ overline{b} = 2overline{p}-overline{q} $, если известны их длины $ |overline{p}| = 2 $, $ |overline{q}| = 3 $ и угол между ними $ varphi = frac{pi}{3} $

Решение

Вычисляем векторное произведение: $$ [overline{a},overline{b}] = [overline{p}+overline{q}, 2overline{p}-overline{q}] = $$ Выполняем попарное умножение слагаемых, из которых состоят векторы: $$ = 2[overline{p},overline{p}] – [overline{p},overline{q}] + 2 [overline{q},overline{p}]-[overline{q},overline{q}] = $$ $$ = 2 cdot 0 – [overline{p},overline{q}] – 2[overline{p},overline{q}]-0 = -3 [overline{p},overline{q}] $$ Берём модуль последнего выражения и подставляем недостающие данные из условия задачи: $$ S = | [overline{a},overline{b}]| = |-3 [overline{p},overline{q}]| = 3cdot |overline{p}| |overline{q}| sin varphi = $$ $$ = 3 cdot 2 cdot 3 sin frac{pi}{3} =18 cdot frac{sqrt{3}}{2} = 9sqrt{3} $$

Ответ

$$ S = 9sqrt{3} $$