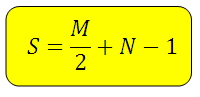Рассмотрим несколько задач на данную тему.
| #1 | #2 | #3 | #4 | #5 |
Задача #1
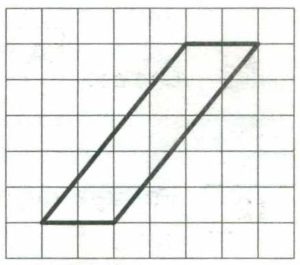
(Номер задачи на fipi.ru — 71E23E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Прежде чем приступать к решению задачи, вспомним теорию >>
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Площадь параллелограмма вычисляется по формуле:
где a — основание параллелограмма, h — высота параллелограмма.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 7, а высота: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 28 ед. кв.
Задача #2
(Номер задачи на fipi.ru — 3BD9B6). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 15 ед. кв.
Задача #3
(Номер задачи на fipi.ru — 5C5046). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 5. Из рисунка также находим высоту параллелограмма: h = 4.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 20 ед. кв.
Задача #4
(Номер задачи на fipi.ru — 566A4E). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 18 ед. кв.
Задача #5
(Номер задачи на fipi.ru — 0275CC). На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания параллелограмма равно: a = 6. Из рисунка также находим высоту параллелограмма: h = 6.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь параллелограмма:
Ответ: площадь параллелограмма равна: 36 ед. кв.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На рисунке изображен параллелограмм ABCD. Используя рисунок, найдите
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)
2
На рисунке с размером клетки 1×1 изображен параллелограмм ABCD. Используя рисунок, найдите
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.5)
3
На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
4
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
5
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
Пройти тестирование по этим заданиям
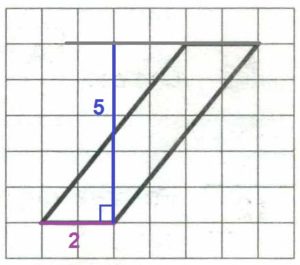
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Источник: ОГЭ 2021 Ященко 36 вариантов.
Решение:
Основание параллелограмма а = 2, высота h = 5:
Найдём его площадь:
S = a·h = 2·5 = 10
Ответ: 10.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 28
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Рубрика Задание 3, Решаем ЕГЭ по математике Комментарии (0)
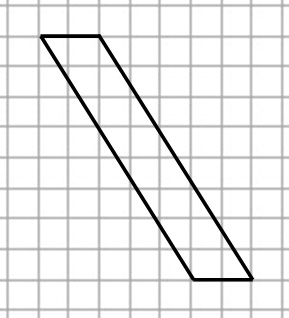
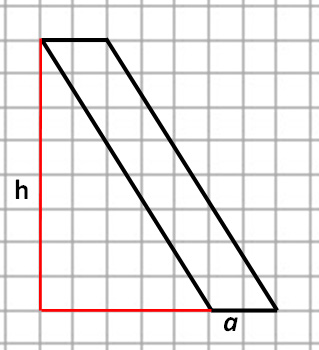
Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению его основания на высоту:
S = a·h, где a – основание, h – высота.
Длину основания и длину высоты легко подсчитать по клеточкам:
a = 2, h = 8
S = 2 · 8 = 16
Ответ: 16
Понравилось? Нажмите
Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.
Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.
В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.
ФОРМУЛА ПИКА
Площадь искомой фигуры можно найти по формуле:
М – количество узлов на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника
*Под «узлами» имеется ввиду пересечение линий.
Найдём площадь треугольника:
Отметим узлы:
1 клетка = 1 см
M = 15 (обозначены красным)
N = 34 (обозначены синим)
Ещё пример. Найдём площадь параллелограмма:
Отметим узлы:
M = 18 (обозначены красным)
N = 20 (обозначены синим)
Найдём площадь трапеции:
Отметим узлы:
M = 24 (обозначены красным)
N = 25 (обозначены синим)
Найдём площадь многоугольника:
Отметим узлы:
M = 14 (обозначены красным)
N = 43 (обозначены синим)
Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.
А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.
Теперь взгляните на следующие фигуры:
Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:
Отметим узлы:
M = 11 (обозначены красным)
N = 5 (обозначены синим)
Ответ: 9,5
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.
Рассмотрим подход оговоренный в статье “Площадь четырёхугольника. Универсальный способ“.
Найдём площадь фигуры:
Опишем около неё прямоугольник:
Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:
Ответ: 4,5
В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.