Содержание:
- § 1 Площадь параллелограмма
- § 2 Решение задачи по теме урока
§ 1 Площадь параллелограмма
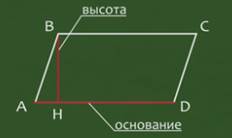
Начертим параллелограмм АВСD, из точки В проведем перпендикуляр ВH к стороне АD.
Сторону АD будем называть основанием, а перпендикуляр ВН – высотой параллелограмма.
Рассмотрим теорему для вычисления площади параллелограмма.
Теорема: Площадь параллелограмма равна произведению его основания на высоту.
Докажем это утверждение.
Дано: параллелограмм АВСD, АD – основание, ВН – высота.
Доказать:S = АD·ВН.
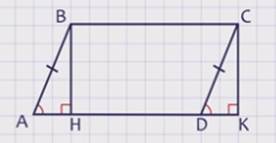
Доказательство:
В данном параллелограмме проведем еще одну высоту СК к стороне АD. Получилась трапеция АВСК, состоящая из параллелограмма АВСD и треугольника DСК. С другой стороны эта трапеция составлена из прямоугольника ВСКН и треугольника АВН. Треугольники АВН и DСК – прямоугольные и равны по гипотенузе и острому углу, действительно, гипотенузы АВ и СD равны как противоположные стороны параллелограмма, а углы ВАН и СDК равны как соответственные углы при пересечении параллельных прямых АВ и СD секущей АD. Значит, площади этих прямоугольных треугольников равны. Следовательно, площадь параллелограмма АВСD равна площади прямоугольника ВСКН. По теореме о площади прямоугольника S = ВС · ВН, а так как ВС = АD, то S = АD · ВН, т.е. площадь параллелограмма равна произведению основания на высоту.
Что и требовалось доказать.
§ 2 Решение задачи по теме урока
Решим задачу.
Задача: Смежные стороны АD и АВ параллелограмма АВСD равны соответственно 32см и 26 см, а один из углов равен 150°. Найдите площадь параллелограмма.
Решение:
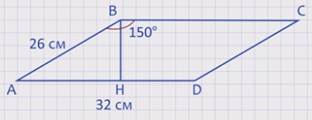
Для решения данной задачи из известного нам тупого угла, пусть это будет угол В, проведем высоту ВН и рассмотрим получившийся прямоугольный треугольник АВН. Угол АВН = 150° – 90° = 60°, тогда угол ВАН = 180° – (90° + 60°) = 30°. По свойству прямоугольного треугольника ВН равна половине гипотенузы АВ, т.е. ВН = 26/2 = 13 см. А площадь параллелограмма равна произведению основания АD на высоту ВН, S= 32 · 13 = 416 см2.
Ответ: площадь параллелограмма равна 416 см2.
Список использованной литературы:
- Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2013.
- Н.Ф. Гаврилова. Поурочные разработки по геометрии. 8 класс. – Москва, «Вако», 2005.
- Л.С. Атанасян и др. Методические рекомендации к учебнику. – Москва, «Просвещение», 2001.
- Д.А. Мальцева. Математика. 9 класс ГИА 2014. – Москва, Народное образование, 2013.
- О.В.Белицкая. Геометрия. 8 класс. Тесты. – Саратов, «Лицей», 2009.
- С.П.Бабенко, И.С. Маркова. Геометрия 8. Комплексная тетрадь для контроля знаний. – Москва, «Аркти», 2014.
Решаем задачи(упражнения) на заказ (!)
.
ПАКЕТ – БЫСТРО (!!!) (примерное время ожидания заказа – 15 минут)
По школьным предметам: математика (алгебра, геометрия), физика, химия.
1 задача – 600 тг/120 руб
Для студентов: математический анализ, линейная алгебра, аналитическая геометрия итд…
1 задача – 1000 тг/200 руб
.
ПАКЕТ – обычный (примерное время ожидания заказа 2 – 24 часа)
По школьным предметам: математика (алгебра, геометрия), физика, химия.
1 задача – 300 тг/60 руб
Для студентов: математический анализ, линейная алгебра, аналитическая геометрия итд…
1 задача – 500 тг/100 руб
.
Для оформления заказа необходимо отправить на whatsaap: +7(707)7328227:
– Скрин чека,
– Фото задач.
.
Реквизиты:
QIWI КОШЕЛЁК: +7(707)2132054
KASPI GOLD: +7(707)2132054, Ернар Галымжанулы
БАНКОВСКИЙ ПЕРЕВОД: 5169 4931 3046 0663 YERNAR USSENBEKOV
_________________________________________________________
Казахстан. Алматы.
Для подготовки к поступлению в НИШ, РФМШ, КТЛ, 165 и 39 лицеи либо для устранения академических пробелов в школе по предметам естественно-математического направления, заполните анкету на сайте https://da-vinci.kz/. Наши отзывчивые менеджера свяжутся с Вами в ближайшее время и дадут Вам более подробную консультацию.
Центр Естественных Наук DA VINCI – один из лидирующих центров города Алматы (Казахстан), основной деятельностью, которого является подготовка школьников к поступлению в различные школы (НИШ, РФМШ, КТЛ итд), а также устранение академических пробелов в школе по предметам естественно-математического направления.
Центр основан в 2011 году и с тех пор, через стены центра прошло около 10000 учеников.
Если Вам понравился данный видеоурок, пожалуйста поддержите наш проект
Реквизиты:
QIWI КОШЕЛЁК: +7(707)2132054
KASPI GOLD: +7(707)2132054, Ернар Галымжанулы
БАНКОВСКИЙ ПЕРЕВОД: 5169 4931 3046 0663 YERNAR USSENBEKOV
Стоимость всего от 1 до 50 рублей  Спасибо Вам! Занимайтесь! Делайте! Достигайте!
Спасибо Вам! Занимайтесь! Делайте! Достигайте!
http://da-vinci.kz/, https://videokursy.kz/
+7 707 729 94 29
Республика Казахстан, г. Алматы, ул. Абая 68/74 угол ул. Ауэзова
Видеоурок как найти площадь параллелограмма

8 класс, 13 урок, Площадь параллелограмма

Геометрия 8 класс. Площадь параллелограмма

Площадь параллелограмма. Геометрия 8 класс.
На этом уроке мы выясним, как найти площадь
параллелограмма. Но прежде следует сказать, что высотой параллелограмма,
проведённой к стороне, называется перпендикуляр, проведённый из любой точки
противолежащей стороны к прямой, содержащей эту сторону.
Например, в параллелограмме ABCD каждый из перпендикуляров АЕ, МN и BК, проведённых соответственно из точек А, М и B к прямой, содержащей сторону CD, является высотой параллелограмма, проведённой к этой стороне.
Перпендикуляры АF и ОP, проведенные
соответственно из точек А и О к прямой, содержащей, сторону BC, являются высотами этого параллелограмма,
проведёнными к стороне BC.
А теперь давайте докажем, что площадь параллелограмма
равна произведению длины стороны на высоту, проведённую к ней.
Доказательство.
Пусть –
параллелограмм.
Докажем, что .
–
прямоугольник.
Докажем, что .
Рассмотрим прямоугольные и
.
как
противолеж. стороны .
как соотв. при
и секущей
.
по
гипотенузе и острому углу.
Значит, .
,
.
Следовательно, .
,
тогда .
как
противолеж. стороны ,
следовательно, .
Что и требовалось доказать.
Теперь для закрепления материала решим несколько
задач.
Задача. Длина стороны
параллелограмма равна см, а высота, проведённая к этой стороне, меньше её на
см.
Найдите площадь параллелограмма.
Решение.
см.
–
высота.
(см).
(см2).
Ответ: см2.
Задача. В параллелограмме сторона
см,
сторона см,
а .
Найдите площадь параллелограмма.
Решение.
Проведём из вершины А высоту АЕ.
Треугольник АЕD является прямоугольным.
–
прямоугольный.
Так как ,
(см).
(см).
,
(см2).
Ответ: см2.
Задача. Высоты,
проведённые к сторонам и
параллелограмма
,
равны см
и см
соответственно. Найдите длину стороны ,
если см.
Решение.
Пусть ABCD – данный параллелограмм. CE – высота, проведённая к стороне AD и равная 3 сантиметрам. CK – высота, проведённая к стороне AB и равная 2 сантиметрам.
Найдём площадь данного параллелограмма.
,
(см2).
,
,
,
(см).
Ответ: см.
Задача. Длина стороны параллелограмма
равна
см,
а его периметр равен 32 см. Найдите высоту, проведённую к стороне ,
если высота ,
проведённая к стороне ,
равна 3 см.
Решение.
,
,
,
,
,
,
(см).
,
3
(см2).
,
,
,
(см).
Ответ: см.
На этом уроке мы с вами выяснили, что называют высотой
параллелограмма, а также как находить площадь параллелограмма.
