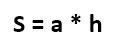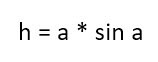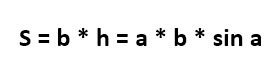Можно ли вписать окружность в параллелограмм и наоборот
Содержание:
-
Параллелограмм, вписанный в окружность
- Свойство радиуса окружности, описанной около прямоугольника
- Пример решения задачи. Параллелограмм и описанная окружность
-
Параллелограмм, описанный около окружности
- Радиус окружности, вписанной в ромб
- Задачи. Параллелограмм и вписанная окружность.
Параллелограмм, вписанный в окружность
Параллелограмм — это четырехугольник с попарно параллельными и равными противолежащими сторонами.
Все четыре стороны этой фигуры принадлежат одной плоскости.
Четырехугольник можно вписать в окружность, если сумма его противоположных углов равна 180°. Если сумма противоположных углов параллелограмма равна 180°, то такой параллелограмм — прямоугольник.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Точка пересечения диагоналей прямоугольника является центром описанной окружности.
Свойство радиуса окружности, описанной около прямоугольника
Радиус описанной окружности равен половине диагонали прямоугольника.
Пример решения задачи. Параллелограмм и описанная окружность
Задача 1
Дано: прямоугольник со сторонами 8 см и 6 см.
Найти: радиус описанной окружности.
Решение: диагональ прямоугольника равна (sqrt{8^2+6^2}=10 (см)); следовательно, радиус описанной окружности равен 10÷2=5 (см).
Ответ: 5 см.
Параллелограмм, описанный около окружности
Когда параллелограмм можно описать около окружности? Другими словами — при каком условии можно вписать окружность или круг в параллелограмм?
Так как параллелограмм — это частный случай четырехугольника, будет действовать то же правило, что и для любого другого четырехугольника. Окружность можно вписать в параллелограмм, только если суммы его противоположных сторон равны.
Это условие выполняется только для тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба).
Если в задаче дано, что в параллелограмм вписана окружность, то из этого условия можно сделать вывод, что все его стороны равны, и данный параллелограмм является ромбом. Если по условию один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат.
Радиус окружности, вписанной в ромб
Радиус вписанной в ромб окружности можно найти несколькими способами.
Если известны диагонали и сторона
Формула 1
(r=frac{Dd}{4a}), где:
- r — радиус вписанной окружности;
- а — сторона ромба;
- D — большая диагональ;
- d — меньшая диагональ.
Если известны диагонали
Формула 2
(r=frac{Dd}{2sqrt{D^2+d^2}}), где:
- r — радиус вписанной окружности;
- D — большая диагональ;
- d — меньшая диагональ.
Если известны сторона и угол
Формула 3
(r=frac{a·sinalpha}2), где:
- r — радиус вписанной окружности;
- а — сторона ромба;
- α — острый угол.
Если известны диагонали и угол
Формула 4
(r=frac d2cosalpha/2=frac d{2sqrt2}sqrt{1+cosalpha})
Формула 5
(r=frac D2sin;alpha/2=frac D{2sqrt2}sqrt{1-cosalpha}), где:
- r — радиус вписанной окружности;
- D — большая диагональ;
- d — меньшая диагональ;
- α — острый угол.
Если известны диагонали и сторона
Формула 6
(r=frac{Dsqrt{a^2-D^2/4}}{2a})
Формула 7
(r=frac{dsqrt{a^2-d^2/4}}{2a}), где:
- r — радиус вписанной окружности;
- D — большая диагональ;
- d — меньшая диагональ;
- а — сторона ромба.
Если известна высота ромба
Формула 8
(r=frac h2), где:
- r — радиус вписанной окружности;
- h — высота ромба.
Если известны площадь и полупериметр
Формула 9
(r=frac Sp), где:
- r — радиус вписанной окружности;
- S — площадь ромба;
- p — полупериметр ромба.
Задачи. Параллелограмм и вписанная окружность.
Задача 2
Дано: параллелограмм со вписанной окружностью. Одна из сторон параллелограмма равна 5 см.
Найти: периметр параллелограмма.
Решение: в параллелограмм можно вписать окружность только если это ромб. Четыре стороны ромба равны. Следовательно, периметр данного параллелограмма равен 5·4=20 (см).
Ответ: 20 см.
Задача 3
Дано: параллелограмм MNKP с диагоналями 12 см и 16 см. В MNKP вписана окружность.
Найти: радиус вписанной окружности.
Решение:
Из того, что в параллелограмм MNKP вписана окружность, делаем вывод, что MNKP — ромб.
Параллелограмм MNKP не является квадратом, так как его диагонали не равны. MK=16 см, NP=12 см.
ΔMOP прямоугольный, (∠MOP=90°. MO=8 см, OP=6 см. S_{MОР}=(8·6)÷2=24 (см^2)).
(S_{MNKP}=24·4=96 (см^2)).
По теореме Пифагора ( MP=sqrt{MО^2+ОР^2}=sqrt{8^2+6^2}=10 (см)).
Полупериметр MNKP равен 20 см.
Следовательно, радиус вписанной окружности равен
(r=frac Sp=96÷10=9,6 (см)).
Ответ: 9,6 см.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Площадь параллелограмма
Алик Беникович Айрапетян
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
На данной странице вы можете ознакомиться с разнообразными вариантами формул для вычисления площади параллелограмма.
Здесь же размещены простые в использовании калькуляторы, с помощью которых можно быстро узнать, как найти площадь параллелограмма по двум сторонам, диагоналям и углу между ними, или через другие величины.
Приведены примеры решения подобных задач.
Рассмотрим задачу и разберёмся на примере, как найти площадь параллелограмма по стороне и высоте, опущенной на эту сторону.
Сделаем это для того, чтобы вы могли проследить за ходом решения и выявить ошибки в своих работах, а также для возможности сравнения своего ответа с ответом калькулятора.
Пример 1
Дано:
сторона параллелограмма = $5$ см, высота = $7$ см.
Найти:
площадь параллелограмма $S$.
Решение:
$S = 5 cdot 7 = 35$ см$^2$.
Ответ:
$S = 35$ см$^2$.
Площадь параллелограмма по стороне и высоте, опущенной на эту сторону
Формула площади параллелограмма по стороне и высоте, опущенной на эту сторону:
$S = b cdot h1$, где
$S$ — площадь параллелограмма,
$b$ — сторона,
$h1$ — высота, опущенная на неё.
Площадь параллелограмма по двум сторонам и углу между ними
Формула площади параллелограмма по двум сторонам и углу между ними:
$S = a cdot b cdot sin (α)$, где
$S$ — площадь параллелограмма,
$a$ — сторона номер один,
$b$ — сторона номер два,
$α$ — угол между сторонами $a$ и $b$.
Чтобы проверить свое понимание темы, рассмотрим также пример задачи на нахождение площади параллелограмма по основанию и высоте и также сверим свой ответ с результатом калькулятора.
Пример 2
Дано:
основание $a = 10$ см, высота $h = 7$ см.
Найти:
площадь параллелограмма $S$.
Решение:
$S = 10 cdot 7 = 70$ см$^2$.
Ответ:
$S = 70$ см$^2$.
Площадь параллелограмма по основанию и высоте
Формула площади параллелограмма по основанию и высоте:
$S = a cdot h$, где
$S$ — площадь параллелограмма,
$a$ — основание,
$h$ — высота.
Площадь параллелограмма по двум диагоналям и углу между ними
Формула площади параллелограмма по двум диагоналям и углу между этими диагоналями:
$S = d1 cdot d2 cdot sin (α)$, где
$S$ — площадь параллелограмма,
$d1$ — первая диагональ,
$d2$ — вторая диагональ,
$α$ — угол между диагоналями $d1$ и $d2$.
В качестве ещё одного примера рассмотрим задачу на нахождение площади параллелограмма по вписанной окружности и стороне.
Пример 3
Дано:
сторона параллелограмма $a = 6$ см, радиус вписанной окружности = $5$ см.
Найти:
площадь параллелограмма $S$.
Решение:
$S = 2 cdot 6 cdot 5 = 60 $ см$^2$.
Ответ:
$S = 60 $ см$^2$.
Площадь параллелограмма по вписанной окружности и стороне
Формула площади параллелограмма по вписанной окружности и стороне:
$S = 2 cdot a cdot r$, где
$S$ — площадь параллелограмма,
$a$ — сторона,
$r$ — радиус вписанной окружности.
Площадь параллелограмма по вписанной окружности и углу между сторонами
Формула площади параллелограмма по вписанной окружности и углу между сторонами:
$S = frac{4 cdot R^2} {sin (α)}$, где
$S$ — площадь параллелограмма,
$R$ — радиус вписанной окружности,
$α$ — угол между сторонами.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 10.06.2019
Здравствуйте, дорогие читатели канала. В этой статье рассмотрим решение 25 задачи из ОГЭ по математике.
Задача: В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 14 и 7. Найдите площадь параллелограмма ABCD
Решение:
Выполним построение чертежа и напишем, что нам известно:
Начнем решать задачу с “конца”, т.е. с того что нам нужно найти.
1) Площадь параллелограмма можно найти двумя способами:
2) Рассмотрим первую формулу площади параллелограмма. На рисунке нам не хватает высоты. Продолжим OF до стороны ВС получим EF=h.
В этой формуле мы не знаем сторону AD.
3) Рассмотрим вторую формулу площади параллелограмма через площадь треугольника.
Площадь треугольника с вписанной окружностью можно найти по следующей формуле:
Для того чтобы найти полупериметр, проведем еще один радиус ON окружности к стороне АВ.
Теперь подставим значение полупериметра в формулу площади треугольника, получаем:
Чтобы найти АК рассмотрим прямоугольный треугольник АОК.
Значит площадь параллелограмма через треугольник равна:
4) Из второго и третьего пункта возьмем получившиеся формулы площади параллелограмма, приравняем их и найдем сторону AD = BC:
Теперь ответим на главный вопрос задачи. Площадь параллелограмма равна:
Если вы знаете способ решения легче, пишите в комментариях.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
- В параллелограмме противоположные стороны и противоположные углы равны.
- Диагонали параллелограмма точкой пересечения делятся пополам.
- Диагональ параллелограмма делит параллелограмм на два равных треугольника.
- Точка пересечения диагоналей — центр симметрии параллелограмма.
- Биссектриса любого угла параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы параллелограмма, проведенные из противоположных углов, параллельны.
- Биссектрисы параллелограмма, проведенные из соседних углов, перпендикулярны.
- Угол между высотами, проведенными из тупого угла параллелограмма, равен острому углу параллелограмма.
- Угол между высотами, проведенными из острого угла параллелограмма, равен тупому углу параллелограмма.
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов сторон параллелограмма.
- Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Частные случаи параллелограмма: прямоугольник, квадрат, ромб. Следовательно, все эти фигуры обладают свойствами, присущими параллелограмму.
Прямоугольник — параллелограмм, у которого все углы равны.
Отличительное свойство прямоугольника: диагонали прямоугольника равны.
Ромб — параллелограмм, у которого все стороны равны.
Отличительное свойство ромба: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат — параллелограмм, у которого все стороны и углы равны.
Отличительное свойство квадрата: диагонали квадрата равны, взаимно перпендикулярны и делят углы квадрата пополам.
Площадь параллелограмма:
- Площадь параллелограмма через сторону и высоту, проведенной к этой стороне: S=a·ha=b·hb.
- Площадь параллелограмма через стороны и угол между ними: S=a·b·sinφ.
- Площадь параллелограмма через диагонали и угол между ними: S=0,5·d1·d2·sinφ.
- Площадь параллелограмма через радиус вписанной окружности и сторону(верна только для параллелограмма, в который можно вписать окружность): S=2·a·r.
- Площадь параллелограмма через радиус вписанной окружности и угол между сторонами(верна только для параллелограмма, в который можно вписать окружность): S=4r2/sinφ.
Как найти площадь параллелограмма — три основных формулы
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья на еще одну математическую тему. Мы расскажем, как правильно посчитать площадь параллелограмма. Эту тему подробно изучают только в 8-м классе. И это говорит, что она не такая простая.
Но для начала давайте все-таки напомним, какая фигура называется параллелограммом.
Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.
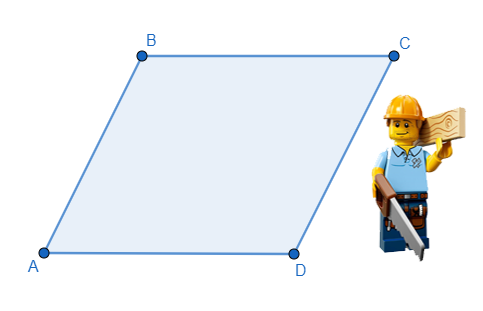
Классический параллелограмм выглядит вот так:
Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.
Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.
И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».
Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.
Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.
Формулы для расчета площади параллелограмма
Есть три основных формулы для вычисления площади параллелограмма:
- если известна длина стороны и высота, проведенная к ней;
- если известны длины сторон и углы между ними;
- если известны длины диагоналей и угол между ними.
Теперь о каждом из этих способов подробнее.
Как найти площадь параллелограмма, если известны сторона и высота
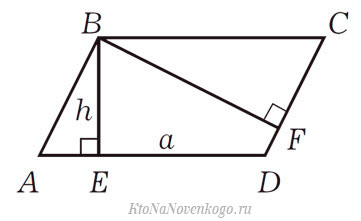
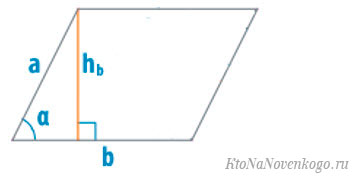
Возьмем для примера такой параллелограмм:
В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.
В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.
И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.
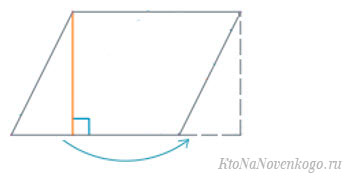
Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:
В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.
Формула площади параллелограмма, если известны стороны и угол
Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.
Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.
Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:
Соответственно, чтобы посчитать значение высоты надо:
И наша конечная формула для расчета площади будет выглядеть следующим образом:
Как найти площадь параллелограмма через диагонали
Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.
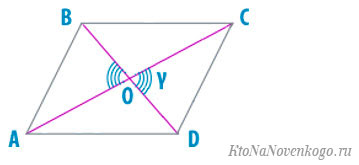
В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:
Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.
Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.