Как найти площадь параллелограмма — три основных формулы
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья на еще одну математическую тему. Мы расскажем, как правильно посчитать площадь параллелограмма. Эту тему подробно изучают только в 8-м классе. И это говорит, что она не такая простая.

Но для начала давайте все-таки напомним, какая фигура называется параллелограммом.
Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.
Классический параллелограмм выглядит вот так:

Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.
Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.

И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».
Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.
Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.
Формулы для расчета площади параллелограмма
Есть три основных формулы для вычисления площади параллелограмма:
- если известна длина стороны и высота, проведенная к ней;
- если известны длины сторон и углы между ними;
- если известны длины диагоналей и угол между ними.
Теперь о каждом из этих способов подробнее.
Как найти площадь параллелограмма, если известны сторона и высота
Возьмем для примера такой параллелограмм:
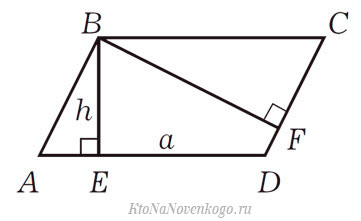
В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.
В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.
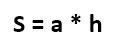
И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.
Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:
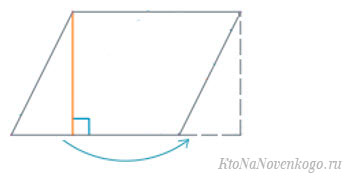
В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.
Формула площади параллелограмма, если известны стороны и угол
Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.
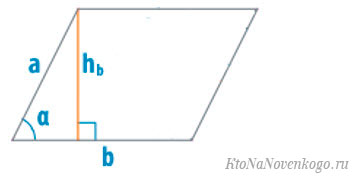
Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.
Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:
![]()
Соответственно, чтобы посчитать значение высоты надо:
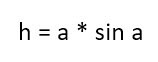
И наша конечная формула для расчета площади будет выглядеть следующим образом:
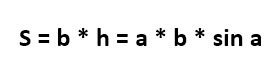
Как найти площадь параллелограмма через диагонали
Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.
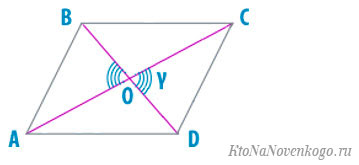
В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:
![]()
Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.
Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.
А) Пусть одна сторона параллелограмма – a; другая – b. Так как площадь параллелограмма равна произведению стороны на высоту проведенную к этой стороне, то площадь параллелограмма S = a•6 или S = b•8
Получаем 6a = 8b или b = 3a/4
Периметр параллелограмма равен 2a + 2b = 42. Подставляем b.
Получаем 2а + 3а/2 = 42
а = 42•2/7 = 12 см
S = 12•6 = 72 см²
Ответ: S = 72 см²
Б) Проведя высоту имеем прямоугольный треугольник с гипотенузой = 5, катетом = 4 (катет меньше гипотенузы) и катетом = h. По теореме Пифагора h = √(25-16) = 3 см
И площадь равна произведению стороны на высоту к данной стороне
S = 3•(4+6) = 30 см²
Ответ: S = 30 см²
В) Тут надо знать формулу, что площадь параллелограмма равна произведению сторон на синус угла между ними.
S = 8•10•sin30˚ = 80•1/2 = 40 см²
Ответ: S = 40 см²
Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.
Онлайн-калькулятор площади параллелограмма
Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.
Рассмотрим несколько способов и формул с последующим решением простых примеров.
Формула площади параллелограмма по основанию и высоте
Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением. Для начала разберем обобщенный случай без использования чисел.
Пусть дан произвольный параллелограмм с основанием aa, боковой стороной bb и высотой hh, проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:
S=a⋅hS=acdot h
aa — основание;
hh — высота.
Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.
Найти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).
Решение
a=10a=10
h=5h=5
Подставляем в нашу формулу. Получаем:
S=10⋅5=50S=10cdot 5=50 (см. кв.)
Ответ: 50 (см. кв)
Формула площади параллелограмма по двум сторонам и углу между ними
В этом случае искомая величина находится так:
S=a⋅b⋅sin(α)S=acdot bcdotsin(alpha)
a,ba, b — стороны параллелограмма;
αalpha — угол между сторонами aa и bb.
Теперь решим другой пример и воспользуемся вышеописанной формулой.
Найти площадь параллелограмма если известна сторона aa, являющаяся основанием и с длиной 20 (см.) и периметр pp, численно равный 100 (см.), угол между смежными сторонами (aa и bb) равен 30 градусам.
Решение
a=20a=20
p=100p=100
α=30∘alpha=30^{circ}
Для нахождения ответа нам неизвестна лишь вторая сторона данного четырехугольника. Найдем ее. Периметр параллелограмма дается формулой:
p=a+a+b+bp=a+a+b+b
100=20+20+b+b100=20+20+b+b
100=40+2b100=40+2b
60=2b60=2b
b=30b=30
Самое сложное позади, осталось только подставить наши значения для сторон и угла между ними:
S=20⋅30⋅sin(30∘)=300S=20cdot 30cdotsin(30^{circ})=300 (см. кв.)
Ответ: 300 (см. кв.)
Формула площади параллелограмма по диагоналям и углу между ними
S=12⋅D⋅d⋅sin(α)S=frac{1}{2}cdot Dcdot dcdotsin(alpha)
DD — большая диагональ;
dd — малая диагональ;
αalpha — острый угол между диагоналями.
Даны диагонали параллелограмма, равные 10 (см.) и 5 (см.). Угол между ними 30 градусов. Вычислить его площадь.
Решение
D=10D=10
d=5d=5
α=30∘alpha=30^{circ}
S=12⋅10⋅5⋅sin(30∘)=12.5S=frac{1}{2}cdot 10 cdot 5 cdotsin(30^{circ})=12.5 (см. кв.)
Ответ: 12.5 (см. кв.)
Решение контрольной работы по геометрии онлайн – от профильных экспертов Студворк!
Тест по теме «Площадь параллелограмма»
1. Формула площади параллелограмма через стороны и углы

a, b – стороны параллелограмма
α, β – углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):

Калькулятор – вычислить, найти площадь параллелограмма:
a(сторона)=
b(сторона)=
α или β (угол в градусах)= ( sin α=sin β )
S=
2. Формула площади параллелограмма через сторону и высоту

a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D – большая диагональ
d –меньшая диагональ
α, β – углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):

Калькулятор – вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
Преподаватель который помогает студентам и школьникам в учёбе.
Площадь параллелограмма – определение и вычисление с примерами решения
Теорема (о площади параллелограмма). Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Доказательство:
Пусть 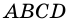
1) Проведем высоту 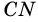 к прямой, содержащей сторону
к прямой, содержащей сторону 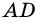 параллелограмма.
параллелограмма.
2) 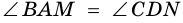 (как соответственные углы при параллельных прямых
(как соответственные углы при параллельных прямых 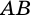 и
и 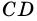 и секущей
и секущей 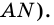 Поэтому
Поэтому 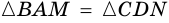 (по гипотенузе и острому углу).
(по гипотенузе и острому углу).
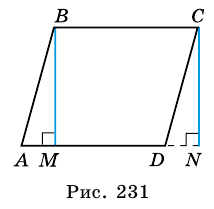
3) Параллелограмм 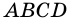 состоит из трапеции
состоит из трапеции 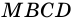 и треугольника
и треугольника 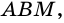 а прямоугольник
а прямоугольник 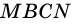 – из трапеции
– из трапеции 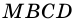 и треугольника
и треугольника 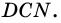 Так как треугольники
Так как треугольники 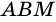 и
и 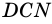 равны, то равны и их площади, а потому равными будут площади параллелограмма
равны, то равны и их площади, а потому равными будут площади параллелограмма 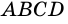 и прямоугольника
и прямоугольника 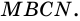
4) 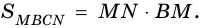 Но
Но 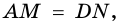 и поэтому
и поэтому 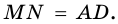 Следовательно,
Следовательно, 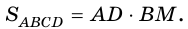
Заметим, что если основание высоты  – точка
– точка  -совпадает с точкой
-совпадает с точкой 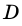 или лежит на продолжении стороны
или лежит на продолжении стороны 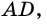 то доказательство теоремы будет аналогичным.
то доказательство теоремы будет аналогичным.
В общем виде формулу площади 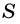 параллелограмма можно записать так:
параллелограмма можно записать так:
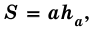
где 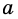 – сторона параллелограмма,
– сторона параллелограмма, 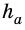 – высота, к ней проведенная.
– высота, к ней проведенная.
Пример:
Докажите, что высоты ромба, проведенные из одной вершины, равны.
Доказательство:
Пусть 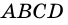 – данный ромб,
– данный ромб,  и
и 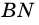 – его высоты (рис. 232).
– его высоты (рис. 232).
Ромб является параллелограммом, поэтому 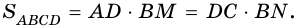 Но
Но 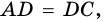 а значит
а значит 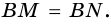
Пример:
Периметр параллелограмма равен 36 см, а его высоты – 4 см и 5 см. Найдите площадь параллелограмма.
Решение:
1) Пусть  – данный параллелограмм,
– данный параллелограмм,  и
и  – его высоты (рис. 232),
– его высоты (рис. 232), 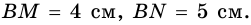
2) 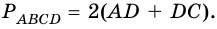 По условию
По условию 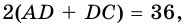 поэтому
поэтому 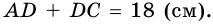
3) Пусть 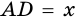 см, тогда
см, тогда 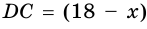 см.
см.
4) Так как по формуле площади параллелограмма 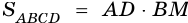 или
или 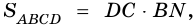 имеем уравнение:
имеем уравнение: 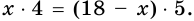 То есть
То есть 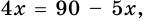 откуда
откуда 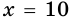 (см).
(см).
5) Тогда 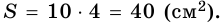
Ответ. 40 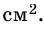
Площадь параллелограмма
С помощью формулы площади прямоугольника можно доказать формулу площади произвольного параллелограмма.
Теорема (формула площади параллелограмма)
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне:
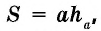
где 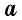 — сторона параллелограмма,
— сторона параллелограмма, 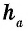 — проведенная к ней высота.
— проведенная к ней высота.
Доказательство:
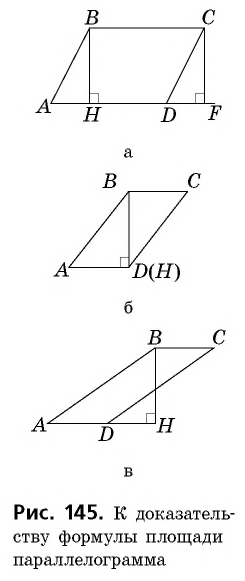
Пусть 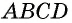 — данный параллелограмм, не являющийся прямоугольником (рис. 145, а). Проведем его высоты
— данный параллелограмм, не являющийся прямоугольником (рис. 145, а). Проведем его высоты 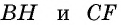 и докажем, что
и докажем, что 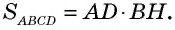 Четырехугольник
Четырехугольник 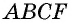 является прямоугольной трапецией, площадь которой можно вычислить двумя способами — как сумму площадей параллелограмма
является прямоугольной трапецией, площадь которой можно вычислить двумя способами — как сумму площадей параллелограмма 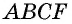 и треугольника
и треугольника 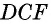 или как сумму площадей прямоугольника
или как сумму площадей прямоугольника 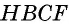 и треугольника
и треугольника 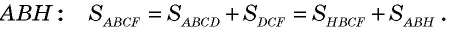 Треугольники
Треугольники 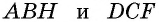 равны по гипотенузе и катету
равны по гипотенузе и катету 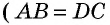 как противолежащие стороны параллелограмма,
как противолежащие стороны параллелограмма, 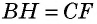 как расстояния между параллельными прямыми). Следовательно, эти треугольники имеют равные площади. Тогда площади параллелограмма
как расстояния между параллельными прямыми). Следовательно, эти треугольники имеют равные площади. Тогда площади параллелограмма 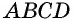 и прямоугольника
и прямоугольника 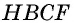 также равны, т.е.
также равны, т.е. 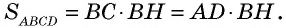 Случаи, когда точка
Случаи, когда точка  не является внутренней точкой отрезка
не является внутренней точкой отрезка  (рис. 145, б, в), рассмотрите самостоятельно.
(рис. 145, б, в), рассмотрите самостоятельно.
Пример:
Площадь параллелограмма равна  а длины его высот — 3 см и 4 см. Найдите периметр параллелограмма.
а длины его высот — 3 см и 4 см. Найдите периметр параллелограмма.
Решение:
Пусть дан параллелограмм с площадью 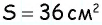 и высотами
и высотами 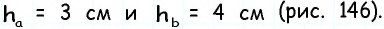 (рис. 146).
(рис. 146).
Поскольку 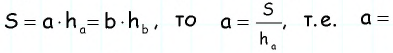
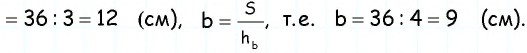
Следовательно, периметр параллелограмма равен 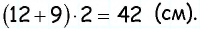
Ответ: 42 см.
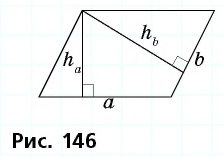
Решая приведенную задачу, можно заметить интересную закономерность: чем больше сторона параллелограмма, тем меньше проведенная к ней высота.
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
- Трапеция и ее свойства
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Четырехугольники и окружность
- Параллелограмм, его свойства и признаки

