По графику скорости от времени v(t) можно найти перемещение тела. Для этого нужно уметь рассчитывать площади плоских фигур.
По-английски «Square» – значит «площадь». Первая буква этого слова – буква «S». Перемещение обозначают буквой S потому, что S – это площадь фигуры, заключенной между линией скорости и горизонтальной осью времени.
Как вычислить площади плоских фигур

Рис.1. Чтобы рассчитать перемещение по графику v(t) нужно уметь вычислять площади трех плоских фигур
Площадь прямоугольника
Площадь прямоугольника (рис. 1а) можно найти, перемножив две его перпендикулярные стороны:
[ large boxed{ S_{text{прямоуг}} = a cdot b }]
Площадь трапеции
Примечание: Трапеция – это четырехугольник, две его стороны параллельные, а две другие – не параллельные. Параллельные стороны называются основаниями трапеции.
Умножив полусумму оснований трапеции на ее высоту, получим площадь (рис. 1б) трапеции:
[ large boxed{ S_{text{трапец}} = frac{1}{2} (a + b) cdot h }]
Площадь прямоугольного треугольника
Для прямоугольного треугольника (рис. 1в) площадь можно вычислить, перемножив два его катета и взяв половину от получившегося произведения:
[ large boxed{ S_{text{треуг}} = frac{1}{2} cdot a cdot b }]
Скорость не меняется
Пусть тело движется по прямой и при этом его скорость не изменяется (остается одной и той же). На языке математики «скорость не изменяется» можно записать так:
[v=const]
На графике для скорости v(t) такая скорость обозначается горизонтальной линией. На рисунке 2 эта линия обозначена синим цветом.

Рис.2. Площадь прямоугольника на графике v(t), если скорость тела не изменяется, будет численно равна перемещению тела
Примечание: Движение с постоянной (т. е. с одной и той же) скоростью называют равномерным движением.
Если скорость направлена по оси движения – линия лежит выше оси t времени (рис. 2а).
А когда скорость направлена против оси движения – линия скорости располагается ниже оси t времени (рис. 2б). Математики в таком случае говорят: «Скорость имеет отрицательную проекцию на ось».
Какую бы проекцию не имела скорость – положительную, или отрицательную, длина вектора скорости остается положительной. Поэтому, когда мы вычисляем площадь фигуры, то не учитываем знак «минус» для скорости (рис. 2б).
В обоих случаях перемещение тела можно вычислить по формуле:
[ large S = v_{0} cdot (t_{2} — t_{1}) ]
Примечание: Перемещение тела – это всегда либо нулевая, либо положительная величина S. Математики словосочетание «либо нулевая, либо положительная» заменят одним словом «не отрицательная».
Скорость увеличивается
Когда скорость тела увеличивается, то линия скорости на графике v(t) всегда располагается так, чтобы с ростом времени удаляться от оси времени. Чем больше времени пройдет, тем дальше от горизонтали располагаются точки, лежащие на линии скорости (рис. 3).

Рис.3. Так выглядит зависимость скорости от времени v(t), когда тело увеличивает свою скорость, двигаясь по оси – рис а) и против оси – рис. б)
Примечание: Движение с возрастающей скоростью называют равноускоренным движением.
Когда тело движется по направлению оси, линия скорости расположена выше горизонтальной оси времени (рис 3а).
А если тело движется против оси, линия скорости располагается ниже горизонтальной оси времени (рис. 3б).
Вычислим перемещение тела, движущегося в положительном направлении оси Ox. Для тела, движущегося противоположно оси, перемещение рассчитывается аналогично.
Выбор интервала времени влияет на то, будем ли мы вычислять площадь трапеции (рис. 4а), или прямоугольного треугольника (рис. 4б).

Рис.4. График v(t) — тело движется в положительном направлении оси и увеличивает свою скорость. От того, какой интервал времени мы выберем, зависит, будем ли мы вычислять путь, пройденный телом, с помощью площади трапеции – рис. а), или прямоугольного треугольника — рис. б)
На графике скорости v(t) для рисунка 4а перемещение с помощью трапеции вычисляется так:
[ large S = frac{1}{2} cdot (v_{1} + v_{2}) cdot (t_{2} — t_{1}) ]
А для рисунка 4б перемещение тела найдем с помощью площади треугольника:
[ large S = frac{1}{2} cdot v_{2} cdot (t_{2} — 0) ]
Скорость уменьшается
Когда тело замедляется и его скорость уменьшается, с ростом времени линия скорости приближается к горизонтальной оси t
- сверху – если тело движется по оси (рис. 5а),
- или снизу – когда тело движется против оси (рис. 5б).

Рис.5. Так выглядит зависимость скорости от времени v(t), когда тело уменьшает свою скорость, двигаясь по оси – рис а) и против оси – рис. б)
Примечание: Движение с уменьшающейся по модулю скоростью называют равнозамедленным движением.
Будем вычислять перемещение тела, движущегося в положительном направлении оси Ox. Аналогичным способом рассчитывается перемещение тела, движущегося противоположно оси.
От того, какой интервал времени нас интересует, зависит, будем ли мы вычислять площадь трапеции (рис. 6а), или треугольника (рис. 6б).

Рис.6. График v(t) — тело движется в положительном направлении оси и уменьшает свою скорость. Выбор интервала времени определяет, будем ли мы вычислять путь, пройденный телом, с помощью трапеции – рис. а), или треугольника — рис. б)
Найдем на графике v(t) перемещение с помощью площади трапеции для рисунка 6а:
[ large S = frac{1}{2} cdot (v_{1} + v_{2}) cdot (t_{2} — t_{1}) ]
А для рисунка 6б перемещение тела найдем с помощью площади треугольника:
[ large S = frac{1}{2} cdot v_{1} cdot (t_{2} — t_{1}) ]
Выводы
На графике v(t) перемещение – это:
- площадь прямоугольника, когда скорость не изменяется;
- площадь треугольника, или трапеции, когда скорость изменяется — падает, или растет.
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
Формула перемещения

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
v = v0 ± at
В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
t1 = t – t2
Когда тело тормозит, через некоторое время t1 оно останавливается. Поэтому скорость в момент времени t1 равна 0:
0 = v01 – at1
При торможении перемещение s1 равно:

Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
t2 = t – t1
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
v = at2
При разгоне перемещение s2 равно:

При этом модуль перемещения в течение всего времени движения равен:
s = |s1 – s2|
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
l = s1 + s2
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с2. Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
v02 = v01 + a1t1 = a1t1 (так как v01 = 0)
Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с2. Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:

Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Задание EF18553
 Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t2(все величины выражены в СИ).
Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t2(все величины выражены в СИ).
Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные и перевести их единицы измерения величин в СИ.
2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.
3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.
4.Определить перемещение тела и его кинетическую энергию.
5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x(t)=x0+v0t+at22
Теперь мы можем выделить кинематические характеристики движения тела:
• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).
Перемещение тела определяется формулой:
s=v0t+at22
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x(t)=v0t+at22=5t−3t2
Кинетическая энергия тела определяется формулой:
Ek=mv22
Скорость при прямолинейном равноускоренном движении равна:
v=v0+at=5−6t
Поэтому кинетическая энергия тела равна:
Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2
Следовательно, правильная последовательность цифр в ответе будет: 34.
Ответ: 34
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18831
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.

Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1 и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s1 и s2, а затем сложим их:

s1 + s2 = 100 + 100 = 200 (м)
Ответ: 200
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 25.4k
Перемещение и путь при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
Когда тело тормозит, через некоторое время t1оно останавливается. Поэтому скорость в момент времени t1 равна 0:
При торможении перемещение s1 равно:

Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
При разгоне перемещение s2 равно:

При этом модуль перемещения в течение всего времени движения равен:
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:

Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

 Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – “>– 3t 2 (все величины выражены в СИ).
Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – “>– 3t 2 (все величины выражены в СИ).
Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x ( t ) = x 0 + v 0 t + a t 2 2 . .
Теперь мы можем выделить кинематические характеристики движения тела:
Перемещение тела определяется формулой:
s = v 0 t + a t 2 2 . .
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2
Кинетическая энергия тела определяется формулой:
Скорость при прямолинейном равноускоренном движении равна:
v = v 0 + a t = 5 − 6 t
Поэтому кинетическая энергия тела равна:
E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2
Следовательно, правильная последовательность цифр в ответе будет: 34.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s1и s2, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить
Уравнение зависимости площади от времени
Рассмотрим некоторые характерные примеры движения тела, знание которых будет полезно при дальнейшем изучении физики.
1.Равномерное прямолинейное движение тела.
При равномерном прямолинейном движении тело совершает равные перемещения `Delta vecr` за одинаковые промежутки времени `Delta t`. Иными словами, скорость `vec v` те ла не зависит от времени и остаётся постоянной в процессе движения:
При этом зависимость `vec r(t)` имеет вид:
`vec r(t)=vec r_0+vec v t`, (7)
где `vec r_0` – радиус-вектор тела в начальный момент времени $$ t=0$$ . В этой связи вспомним замечание о начальных условиях, сделанное в §4. Вектор $$ <overrightarrow>_<0>$$ здесь является тем начальным условием, которое позволяет однозначно определить радиус-вектор $$ overrightarrow$$ тела в любой момент времени в процессе движения.
Векторное уравнение (7) равносильно системе двух скалярных уравнений, выражающих зависимость от времени $$ t $$ координат $$ x$$ и $$ y$$ движущегося тела:
| $$ left<beginxleft(tright)=_<0>+_left(tright),\ yleft(tright)=_<0>+_left(tright)·endright.$$ | (8) |
где $$ _<0>$$ и $$ _<0>$$ – начальные координаты тела в момент времени $$ t=0$$, а $$ _$$ и $$ _$$ -проекции вектора скорости `vecv` на координатные оси $$ Ox$$ и $$ Oy$$ соответственно.
Траектория равномерного прямолинейного движения тела графически представляет собой отрезок прямой линии (рис. 9), тангенс угла наклона которой к оси абсцисс равен отношению проекций скорости на оси координат: $$ mathrmalpha =_/_$$. Аналитическое уравнение траектории, т. е. зависимость $$ yleft(xright)$$, легко получить, исключив параметр $$ t$$ из системы уравнений (8):
Равномерное прямолинейное движение тела на плоскости $$ xOy$$ описывается уравнениями: $$ xleft(tright)=6+3t$$, $$ yleft(tright)=4t$$ (величины измерены в СИ). Запишите уравнение траектории тела. Изобразите графически зависимость модуля вектора скорости от времени $$ vleft(tright)$$. Определите путь, пройденный телом в течение первых пяти секунд движения.
Сравнивая уравнения движения, представленные в условии задачи, с системой уравнений (8), находим:
Уравнение траектории получим, подставив эти значения в общее уравнение (9):
`y(x) =4/3(x – 6)`, или `y(x) = 4/3 x – 8`.
Модуль $$ v$$ скорости тела определим, зная $$ _$$ и $$ _$$:
График зависимости $$ vleft(tright)$$ представлен на рис. 10. При равномерном прямолинейном движении пройденный путь `Delta S` численно равен модулю вектора `Delta vec r` перемещения тела. Вектор `Deltavec r` для такого движения найдём из уравнения (7): `Deltavec r = vec r (t) – vec r_0 = vec vt`. Его модуль равен: `Delta r = vt`. Таким образом, при равномерном движении путь, пройденный телом в течение времени `t`, определяется по формуле `Delta S = vt`, т. е. численно равен площади прямоугольника под графиком зависимости $$ vleft(tright)$$ . Этот вывод можно обобщить и на случай неравномерного движения.
В нашем примере путь равен площади прямоугольника, заштрихованного на рис. 10:
`Delta S = vt = 5 “м”/”c”*5 “c” = 25 “м”`.
Используя рассуждения аналогичные Примеру 3, несложно показать, что пусть численно равен площади фигуры под графиком скорости при любом произвольном движении материальной точки.
Координаты тела при равномерном прямолинейном движении на плоскости $$ xOy $$ за время $$ t=2$$ c изменились от начальных значений $$ _<0>=5$$ м, $$ _<0>=7$$ м до значений $$ x=-3$$ м и $$ y=1$$ м. Найдите модуль скорости тела. Запишите уравнение траектории тела. Изобразите графически траекторию тела и направление вектора его скорости. Постройте графики зависимости координат тела от времени.
Проекции скорости на оси координат можно найти с помощью уравнений движения (8) и численных данных задачи:
Тогда модуль скорости `v=sqrt(v_x^2+v_y^2)=5` м/с.
Уравнение траектории $$ yleft(xright)$$ с учётом (9) и численных данных задачи имеет вид:
Положение тела в начальный и конечный моменты времени (точки `A` и `B`), его траектория и направление скорости изображены на рис. 11. Зависимость координат тела от времени легко найти аналитически, подставляя начальные условия и значения $$ _$$ и $$ _$$ в общие уравнения движения (8):
Графически эти зависимости представлены в виде отрезков прямых на рис. 12.
Заметим, что тангенсы углов наклона отрезков прямых на рис. 12 численно равны коэффициентам при $$ t$$ в соответствующих уравнениях $$ xleft(tright)$$ и $$ yleft(tright)$$, т. е. значениям $$ _$$ и $$ _$$:
(Т. к. в данном случае графики уравнений движения представляют собой убывающие функции, то здесь тангесы отрицательны.)
2. Неравномерное движение тела.
Для неравномерного движения характерно то, что с течением времени изменяется скорость движущегося тела, а в общем случае и его ускорение. В качестве примера может служить движение, при котором тело проходит различные участки своего пути с разной скоростью. Такое движение принято характеризовать, прежде всего, средней путевой скоростью. Причём прилагательное «путевая» в условиях задач часто опускается.
Любитель бега трусцой пробежал половину пути со скоростью $$ _<1>=10$$ км/ч. Затем половину оставшегося времени бежал со скоростью $$ _<2>=8$$ км/ч, а потом до конца пути шёл пешком со скоростью $$ _<3>=4$$ км/ч. Определить среднюю скорость движения бегуна.
Из смысла условия задачи следует, что здесь речь идёт о средней путевой скорости. Разобьём весь путь `Delta S` на три участка `Delta S_1`, `Delta S_2` и `Delta S_3`. Время движения на каждом участке обозначим соответственно `Delta t_1`, `Delta t_2`, `Delta t_3`. Средняя скорость бегуна согласно определению, выраженному формулой (3), будет равна:
`v_”cp”= (Delta S_1 +Delta S_2+Delta S_3)/(Delta t_1+Delta t_2+Delta t_3)`.
По условию задачи `Delta S_1 =DeltaS // 2`, `Delta S_2 + Delta S_3 = Delta S //2`. Поскольку `Delta S_1 = v_1Delta t_1`, `Delta S_2 = v_2Delta t_2`, `Delta S_3 = v_3Delta t_3` и, учитывая, что `Delta t_2 = Delta t_3`, найдём время движения на отдельных участках:
`Delta t_1=(Delta S_1)/(v_1)=(Delta S)/(2v_1)`,
`Delta t_2=(Delta S_2)/(v_2)=(Delta S)/(2(v_2+v_3))`,
`Delta t_3=(Delta S_3)/(v_3)=(Delta S)/(2(v_2+v_3))`.
Подставляя эти значения в выражение для `v_”ср”`, получим:
`v_”cp”=(Delta S)/((Delta S)/(2v_1)+(Delta S)/(2(v_2+v_3))+(Delta S)/(2(v_2+v_3))) =(2v_1(v_2+v_3))/(2v_1+v_2+v_3)=7,5` км/ч.
Заметим, что иногда учащиеся подсчитывают среднюю путевую скорость движения по формуле `v_”ср”= (v_1 + v_2 + . + v_n)//n`, где `v_i` – скорость движения на `i`-м участке, `n` – число участков пути. Аналогично поступают и с вектором средней скорости `v_”ср”`. Следует иметь в виду, что такой расчёт в общем случае является ошибочным.
Другим характерным примером неравномерного движения служит так называемое равнопеременное движение, которое целесообразно рассмотреть подробно, не выходя при этом за рамки школьной программы.
3. Равнопеременное движение.
Равнопеременным называется такое неравномерное движение, при котором скорость `vec v` за любые равные промежутки времени `Delta t` изменяется на одинаковую величину `Deltavecv`. В этом случае ускорение `veca` тела не зависит от времени и остаётся постоянным в процессе движения:
(при этом `vec v != “const”`, и траектория движения не обязательно прямолинейная).
При равнопеременном движении скорость $$ overrightarrow$$ тела изменяется с течением времени по закону
`vec v (t)=vec v_0 +vec at`, (11)
где `vecv_0` – скорость тела в начальный момент времени `t=0`.
В свою очередь, зависимость `vecr(t)` имеет вид:
`vec r(t)=vec r_0+vec v_0t+(vec a t^2)/2`, (12)
где `vecr_0` – начальный радиус-вектор тела при `t=0`. Вновь заметим, что величины `vecv_0` и `vecr_0` представляют собой начальные условия, позволяющие в любой момент времени однозначно определить векторы `vecv` и `vecr`.
При координатном способе описания равнопеременного движения векторным уравнениям (11) и (12), равносильны следующие системы уравнений для проекций скорости и радиус-вектора тела на оси выбранной системы отсчёта. Здесь мы ограничиваемся случаем плоского движения, при котором траектория тела лежит в одной плоскости, совпадающей с координатной:
| $$ left<begin_left(tright)=_<0x>+_t,\ _left(tright)=_<0y>+_t.endright.$$ | (13) |
| $$ left<beginxleft(tright)=_<0>+_<0x>t+<displaystyle frac<_^<2>><2>>,\ yleft(tright)=_<0>+_<0y>t+<displaystyle frac<_^<2>><2>>,endright.$$ | (14) |
В случае прямолинейного движения тела удобнее одну координатную ось, например ось $$ Ox$$, совместить с траекторией тела. Тогда для описания движения будет достаточно одной этой оси, в проекциях на которую векторные уравнения (11) и (12) дают:
Если на промежутке времени от $$ 0$$ до $$ t$$ направление движения тела не изменялось на противоположное, то разность $$ x-_<0>$$текущей и начальной координат тела совпадает с пройденным путём $$ S$$, следовательно,
Эту формулу можно записать по-другому, если подставить в неё время $$ t$$, выраженное из уравнения $$ _=_<0x>+_t$$ . Это время будет
Тогда для пути $$ S$$ после несложных преобразований получим
Удобство этой формулы заключается в том, что она не содержит времени $$ t$$ в явном виде. Вместе с тем надо помнить, что формула получена в предположении о неизменности направления движения тела.
За `2`c прямолинейного равноускоренного движения тело прошло `20` м, увеличив свою скорость в `3` раза. Определите конечную скорость тела. (ЕГЭ, 2005г., уровень .B )
Пусть за время $$ t=2$$ с скорость тела изменилась от $$ _<0>$$ до $$ v$$. Направим координатную ось $$ Ox$$ вдоль траектории тела в сторону движения. Тогда в проекциях на эту ось можно записать `v=v_0+at`, `a` – модуль ускорения тела. По условию `v_0=1/3v` и, следовательно, `a=2/3v/t`.
За время $$ t$$ тело, движущееся с таким ускорением, пройдёт путь
С учётом выражений для $$ _<0>$$ и $$ a$$ получим `S=2/3vt`. Откуда искомая скорость `v=3/2S/t`. Подставляя сюда значения `S = 20` м и `t =2` c, найдём окончательно `v =15` м/ с.
Одним из наиболее наглядных примеров равнопеременного движения является движение тела в поле тяжести Земли, которое мы имеем возможность наблюдать повседневно. Для решения задач в этом случае надо заменить в приведённых выше формулах вектор $$ overrightarrow$$ на ускорение свободного падения $$ overrightarrow$$, сообщаемое силой гравитационного притяжения всякому телу, движущемуся в поле тяжести Земли. Рассмотрим три конкретных случая такого движения.
Движение тела, брошенного вертикально.
Тело бросили с поверхности земли, сообщив ему начальную скорость $$ <overrightarrow>_<0>$$ направленную вертикально вверх. Пренебрегая сопротивлением воздуха, определите время $$ tau $$ полёта тела до момента падения на землю; скорость тела в момент падения; максимальную высоту $$ H$$ подъёма тела над землёй; время $$ <tau >_<1>$$ подъёма тела на максимальную высоту; путь `S`, пройденный телом за время полёта и перемещение тела. Начертите графики зависимости от времени $$ t$$ вертикальной координаты тела и проекции на вертикальную ось его скорости в процессе полёта.
Поскольку движение полностью происходит в вертикальном направлении, то для определения пространственного положения тела достаточно одной координатной оси $$ Oy$$. Направим её вертикально вверх, начало отсчёта $$ O$$ поместим в точку бросания (рис. 13). Начальные условия движения тела: $$ _<0>=0,_<0y>=_<0>$$.
Пусть при $$ t=tau $$ тело упало на землю. В этот момент $$ y=0$$ и уравнение (16) даёт: `0=v_0 tau-(g t^2)/2`. Откуда для $$ tau $$ получаем: $$ tau =0$$ или `tau=(2v_0)/g`. Значение $$ tau =0$$ соответствует начальному моменту бросания тела с поверхности земли, и для нас интереса не представляет. Следовательно, время полёта тела `tau=(2v_0)/g`.
Согласно (15), при $$ t=tau $$ имеем: $$ _=_<0>-gt$$. Тогда с учётом найденного значения $$ tau $$ получим $$ _=_<0>-2_<0>=-_<0>$$. Таким образом, скорость тела в момент падения равна по величине начальной скорости $$ _<0>$$, но направлена вертикально вниз, её проекция на ось $$ Oy$$ отрицательна.
Пусть при $$ t=<tau >_<1>$$ тело находится в наивысшей точке подъёма. Это значит, что $$ y=H,_=0$$. С учётом этих значений уравнения (15) и (16) дают:
`0=v_0-g tau_1`, `H=v_0 tau_1-(g tau_1^2)/2`.
Из первого уравнения определяем время подъёма тела `tau_1=(v_0)/g` и, подставляя $$ <tau >_<1>$$ во второе уравнение, найдём `H=(v_0^2)/(2g)`.
Заметим, что время $$ <tau >_<1>$$ подъёма тела на максимальную высоту вдвое меньше времени $$ tau $$ полёта тела: $$ tau =2<tau >_<1>$$.
Путь $$ S$$, пройденный телом за время полёта, складывается из двух участков: подъёма до высшей точки траектории и падения с высшей точки траектории на поверхность земли. Очевидно, что длины траекторий движения тела на этих участках одинаковы и, значит, $$ S=2H$$. Перемещение тела равно нулю, поскольку начальная и конечная точки траектории тела совпадают.
Зависимость $$ yleft(tright)$$ в соответствии с (16) представляет собой квадратичную функцию, графиком которой, как известно, является парабола (рис. 14). Ветви параболы направлены вниз, т. к. в формуле (16) коэффициент при `t^2` отрицателен.
Зависимость $$ _left(tright)$$ является линейной, и её график представляет собой отрезок прямой линии (рис. 15), тангенс угла наклона которой коси абсцисс равен коэффициенту при $$ t$$ в формуле (15):
Движение тела, брошенного горизонтально.
Тело бросили с высоты $$ H$$ над поверхностью земли, сообщив ему начальную скорость $$ <overrightarrow>_<0>$$, направленную горизонтально (рис. 16). Пренебрегая сопротивлением воздуха, определите время $$ tau $$ полёта тела до его падения на землю, дальность $$ l$$ полёта тела, скорость `vecv` тела в момент падения. Выбрав прямоугольную систему координат так, как показано на рис. 16, запишите уравнение траектории движения тела, начертите графики зависимости от времени $$ t$$ координат тела и проекций скорости тела на координатные оси.
Начало отсчёта $$ O$$ поместим на поверхности земли под точкой бросания (рис. 16). Начальные условия движения тела: `x_0=0`, `y_0=H`, `v_(0x)=v_0`, `v_(0y)=0`. Проекции ускорения тела на оси координат при отсутствии сопротивления воздуха равны:
Запишем системы уравнений (13) и (14) с учётом этих значений:
| $$ left<begin_=_<0>,\ _=-gt·endright.$$ | (17) |
| $$ left<beginx=_<0>t,\ y=H-<displaystyle frac^<2>><2>>·endright.$$ | (18) |
Пусть при $$ t=tau $$ тело упало на землю. Это означает, что $$ y=0$$, $$ x=l$$, и уравнения системы (18) принимают вид:
Решая их ,находим:
`tau= sqrt((2H)/g)`, `l=v_0sqrt((2H)/g)`.
В свою очередь, система уравнений (17) даёт: $$ _=_<0>,_=-gtau $$. С учётом значения $$ tau $$ получим `v_y=-sqrt(2gH)`, и модуль скорости `vecv` будет равен:
Направление вектора `vecv` определим с помощью угла $$ alpha $$ (рис. 16):
Уравнение $$ yleft(xright)$$ траектории движения тела получим, исключив параметр $$ t$$ из системы (18):
Так как $$ yleft(xright)$$ представляет собой квадратичную функцию, то траекторией движения тела является участок параболы с вершиной в точке бросания. Ветви параболы направлены вниз. Графики, требуемые в условии данного примера, представлены соответственно на рис. 17 и рис. 18.
Движение тела, брошенного под углом к горизонту.
Тело бросили с поверхности земли с начальной скоростью $$ _<0>$$ направленной под углом $$ alpha $$ к горизонту (рис. 19). Пренебрегая сопротивлением воздуха, определите время $$ tau $$ полёта тела до его падения на землю,дальность $$ l$$ полёта тела, скорость тела в момент падения на землю,максимальную высоту $$ H$$ подъёма тела над землёй, время $$ <tau >_<1>$$ подъёма тела на максимальную высоту. Запишите уравнение траектории тела.
Направим оси прямоугольной системы координат, как показано на рис. 19. Начало отсчёта $$ O$$ поместим в точку бросания. Тогда начальные условия движения тела таковы: `x_0=0`, `y_0=0`, `v_(0x)=v_0cosalpha`, `v_(0y)=v_0sinalpha`. При отсутствии сопротивления воздуха $$ _=0,_=g$$ С учётом этих значений системы уравнений (13) и (14) имеют вид:
| $$ left<begin_=_<0>mathrmalpha ,\ _=_<0>mathrmalpha -gt·endright.$$ | (19) |
| $$ left<beginx=left(_<0>mathrmalpha right)t,\ y=left(_<0>mathrmalpha right)t-<displaystyle frac^<2>><2>>·endright.$$ | (20) |
Пусть при $$ t=tau $$ тело упало на землю, тогда: $$ y=0,x=l$$. Уравнения системы (20) дают:
(Здесь использовано равенство $$ 2mathrmalpha mathrmalpha =mathrm2alpha .$$ )
Из полученного выражения для $$ l$$ легко определить угол $$ alpha $$, при котором дальность полёта тела будет максимальной. Действительно, величина $$ l$$ как функция от $$ alpha $$ принимает максимальное значение в том случае, когда $$ mathrm2alpha =1$$. Это возможно, если `2alpha=90^@`, т. е. `alpha=45^@`.
Модуль скорости тела в момент падения на землю определим с помощью теоремы Пифагора: `v=sqrt(v_x^2+v_y^2)`. В соответствии с системой уравнений (19) в этот момент (при $$ t=tau $$ ) имеем: $$ _=_<0>mathrmalpha $$, $$ _=_<0>mathrmalpha -gtau =-_<0>mathrmalpha $$.
Направление скорости тела в момент падения составляет угол $$ alpha $$ с направлением оси $$ Ox$$. Этот угол отсчитывается по часовой стрелке от направления оси $$ Ox$$.
Пусть при $$ t=<tau >_<1>$$ тело достигло максимальной высоты. В этот момент $$ _=0$$, `y=H`. Соответствующие уравнения систем (19) и (20) дают:
Отсюда последовательно находим:
Уравнение траектории получим, исключив из системы (20) время $$ t$$ :
График траектории тела представляетсобой участок параболы, ветви которой направлены вниз.
Уравнение зависимости площади от времени
Графическое представление равномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V (t) – изменение скорости со временем
S(t) – изменение перемещения (пути) со временем
a(t) – изменение ускорения со временем

За висимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно ( v = const ), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) – прямая линия, параллельная оси времени.

Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

Зависимость перемещения от времени. График s(t) – наклонная линия :
Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Неравномерное прямолинейное движение.
Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.
Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.
Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
Различие между средней и мгновенной скоростями показано на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.
Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

Vx — Скорость тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
ax — Ускорение тела
t — Время движения тела
Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.
Единица измерения ускорения в СИ [м/с 2 ].
Ускорение измеряют акселерометром
Уравнение скорости для равноускоренного движения: vx = vxo + axt
Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

Sx — Перемещение тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
Vx — Скорость тела при равноускоренном движении по прямой
ax — Ускорение тела
t — Время движения тела
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

– если известны начальная, конечная скорости движения и ускорение.

– если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V(t) – изменение скорости со временем
S(t) – изменение перемещения (пути) со временем
a(t) – изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости vx = vxo + axt . Графиком является наклонная линия.

Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.


Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:

В координатах зависимость имеет вид:
[spoiler title=”источники:”]
http://zftsh.online/articles/5086
http://www.sites.google.com/site/opatpofizike/teoria/teoria-10-klass/graficeskoe-predstavlenie-dvizenia
[/spoiler]
Перемещение при прямолинейном равноускоренном движении


4
Средняя оценка: 4
Всего получено оценок: 157.
4
Средняя оценка: 4
Всего получено оценок: 157.
Движение, при котором траектория представляет собой прямую линию, называется прямолинейным. Если при таком движении скорость равномерно изменяется, то изменение скорости за единицу времени называется ускорением, а такое движение называется равноускоренным. Рассмотрим перемещение при прямолинейном равноускоренном движении.
Прямолинейное равноускоренное движение
Наиболее удобным для изучения примером равноускоренного прямолинейного движения является свободное падение тел в первые секунды полета, когда сопротивление воздуха пренебрежительно мало. Скорость падения тела при этом равномерно увеличивается, и за одинаковые промежутки времени изменение составляет одну и ту же величину.

Для Земли на средних широтах каждую секунду скорость падения увеличится приблизительно на 9.81 м/с. Данная величина называется ускорением свободного падения.
Если бы движение было равномерным, то материальная точка каждую секунду проходила бы одно и то же расстояние. Однако для равноускоренного движения это не так.
Найдем формулу перемещения тела при прямолинейном равноускоренном движении.
Вывод формулы перемещения
Наиболее просто найти формулу перемещения из графика скорости. Перемещение материальной точки равно площади фигуры, лежащей под графиком скорости.
Например, для равномерного движения график скорости представляет горизонтальную прямую, а значит, площадь под этим графиком является прямоугольником, высота которого равна скорости, а ширина – времени. Для нахождения его площади необходимо перемножить эти величины, получив известную формулу «расстояние равно произведению скорости на время пути».
При равноускоренном движении скорость равномерно меняется, а значит, ее график представляет собой наклонную прямую:
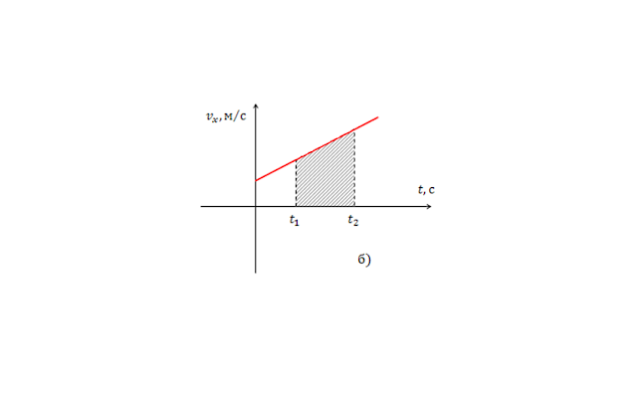
Найдем площадь фигуры под этой прямой.
Фигура является четырехугольником, одна сторона является отрезком оси абсцисс длинной $Δt=t_2-t_1$, две соседние стороны – вертикальные отрезки, длина каждого равна значению скорости в соответствующий момент времени: $v_1$ и $v_2$. То есть, фигура является трапецией, площадь которой, как известно из геометрии, равна произведению полусуммы оснований на высоту. Высота равна промежутку времени, основания – скоростям вначале и в конце пути. То есть, если начальный момент времени нулевой ($t_1=0$), а скорость в начальный момент обозначить $v_0$ то рассматриваемое перемещение равно:
$$x(t)={v+ v_0over 2}t$$
Поскольку при равноускоренном движении скорость за единицу времени увеличивается на величину ускорения, то скорость в момент $t$ будет равна сумме начальной скорости и произведению ускорения на время пути:
$$v(t)= v_0 + at$$
Подставив значение скорости в предыдущую формулу, и приняв, что перемещение в начальный момент времени было равно $x_0$, получим окончательную формулу перемещения тела при прямолинейном равноускоренном движении:
$$x(t)=x_0+v_0t+{at^2over 2}$$
Из вида формулы можно заключить, что график перемещения при равноускоренном движении является параболой.
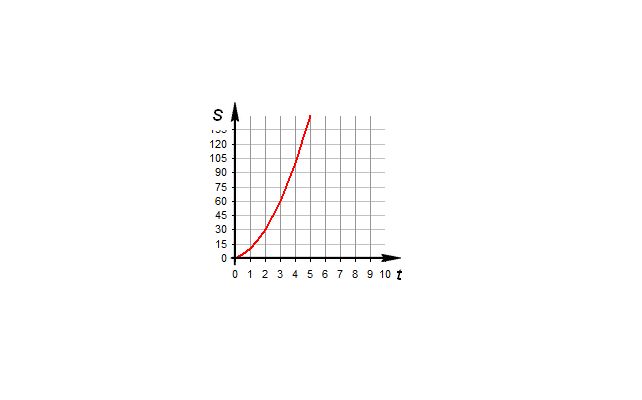
При решении задач время движения зачастую неизвестно, в этом случае удобно выразить его из предыдущей формулы, получив соотношение:
$$x(t)=x_0+{v^2-v_0^2over 2a}$$
Парабола имеет, как правило, два корня. А значит, задачи о перемещении тела при равноускоренном движении могут иметь не одно, а два правильных решения. Например, если найти время, когда предмет, брошенный вверх со скоростью 20м/с достигнет высоты 9 м, мы получим два ответа: через 0.52 с и 3.56 с. Оба эти ответы правильны. Предмет будет на высоте 9 м дважды – первый раз при полете вверх, второй раз в момент падения.

Что мы узнали?
Наиболее частый пример прямолинейного равноускоренного движения – это свободное падение тел, пока сопротивление воздуха пренебрежительно мало. Перемещение при равноускоренном прямолинейном движении является квадратичной функцией, ее график является параболой.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 157.
А какая ваша оценка?
Физика
Тема 2: Кинематика
Урок 8: Графический способ нахождения пути и перемещения
- Видео
- Тренажер
- Теория
Заметили ошибку?
Графический способ нахождения пути и перемещения
При равномерном движении, проекция перемещения на ось х (S x) вычисляется как S x=v x t.
Если мы на графике изобразим зависимость скорости v xот времени, то получим прямую линию, параллельную оси t . Тогда S xна графике – это площадь прямоугольника

Если тело движется против оси х, то проекция скорости vнаправлена против оси х и v x будет отрицательной. Тогда

S x=−vx t.
При неравномерном движении, мы разбиваем проекцию перемещения на маленькие участки, где на каждом участке, скорость практически не менялась и движение равномерно

Сложив площади всех маленьких участков (где площадь каждого участка S x=v x t ¿, мы получим общую площадь под графиком, т. е. проекцию перемещения на ось t .

Задача 1
Электропоезд, отходящий от станции, в течение 0,5 мин двигался с ускорением 0,8 м/с2. Определите путь, который он прошёл за это время, и скорость в конце пути.
Дано

Решение

Задача 2
Тело движется прямолинейно вдоль оси ОХ (рис 8). График зависимости скорости V x от времени представлен на рисунке 7. По данному графику определите перемещение и путь, пройденные телом за время t = 6 с.

Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.

