Пересечение двух окружностей
Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют
Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.
Формулы для расчета приведены под калькулятором.
Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Пересечение окружностей
Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.
При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
| Случай | Описание | Условие |
|---|---|---|
| Тривиальный случай – окружности совпадают (это одна и та же окружность) | ||
| Окружности не касаются друг друга | r1 + r2″ /> | |
| Одна окружность содержится внутри другой и не касается ее | ||
| Окружности пересекаются в двух точках | Не выполнено ни одно из условий выше | |
| Окружности соприкасаются в одной точке | Частный случай предыдущего |
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:
Сначала калькулятор находит отрезок a
Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):
И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:
Обратите внимание на разные знаки перед вторым слагаемым
По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres
Как найти площадь пересечения окружностей
Позволяет рассчитать площадь пересечения двух окружностей произвольных радиусов.
Используются достаточно простые формулы, которые элементарно доказываются.
Дополнительно есть калькулятор, который высчитывает координаты пересечения двух окружностей
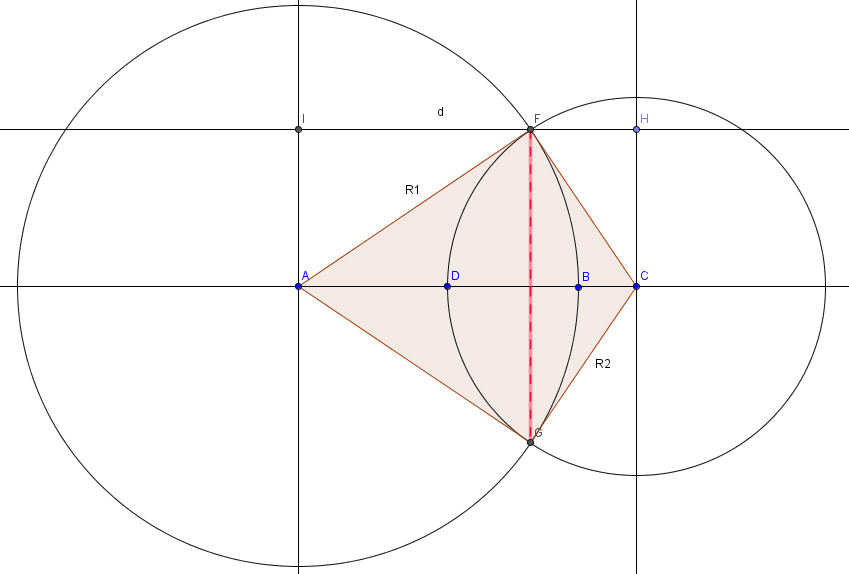
Площадь пересечения двух окружностей состоит из двух сегментов FDG и FBG
Вывести формулу расчета площади пересечения двух окружностей можно из двух общеизвестных формул и знаний решения треугольника:
Формулы сектора окружности
и длина хорды окружности
По известным сторонам треугольника AFС определяем высоту на сторону AC.
Удвоением этой высоты мы получаем длину хорды, после этого узнаем угол альфа по второй формуле.
По известным сторонам треугольника AFG узнаем его площадь. Вычитаем её из площади сектора окружности, ведь угол альфа нам уже известен.
И получаем площадь сегмента FBG
Подобным образом вычисляем FDG
Это лишь один из способов решения задачи вычисления площади пересечения двух окружностей.
– радиус первой окружности
– радиус второй окружности
– расстояние между центрами окружностей
Пример
Хотим узнать площадь пересечения двух окружностей радиусом в 1 и расстоянием между центрами 0.8079455
Пишем okr 1 1 0.8079455
Площадь двух пересекающихся окружностей равна = 1.5707963388681
Первая окружность радиус 4, вторая окружность радиус 2, расстоянием между центрами 3
Пишем okr 4 2 3
Площадь двух пересекающихся окружностей равна = 9.5701994729833
Первая окружность радиус 4, вторая окружность радиус 2, расстоянием между центрами 0
Расчет площади пересечения окружностей методом Монте-Карло
Эта статья родилась как логическое продолжение пятничного поста о методе Бутстрапа, а особенно, комментариев к нему. Не защищая метод Бутстрапа, стоит уделить внимание методам Монте-Карло. Здесь я хочу поделиться своим опытом применения Монте-Карло в одной из своих практических задач, а также обоснованием законности этого применения.
Итак, моя задача заключалась в необходимости вычисления площади фигуры, являющейся пересечением окружностей, с последующей реализацией на языке JavaScript. Площадь под графиком – это интеграл. Интегрирование методом Монте-Карло достаточно широко известно, но, как многие верно заметят, его применение требует некоторого обоснования. За подробностями прошу под кат.
Обоснование
Задача расчета площади пересечения двух окружностей является тривиальной геометрической задачей (координаты центров окружностей и их радиусы нам известны). Площадь пересечения двух окружностей – это сумма площадей соответствующих сегментов этих окружностей. Есть решения для расчета площади пересечения двух, трех, четырех окружностей в различных частных случаях.
А вот решения общего случая для пересечения даже трех окружностей уже далеко не так тривиальны. В процессе поиска я нашел даже исследования по расчету площади пересечения N окружностей, однако они настолько же интересны, насколько и сложны.
Здесь на сцену выходит метод Монте-Карло. Благодаря современным компьютерным мощностям этот метод позволяет провести большое количество статистических испытаний, на основе результатов которых делается обобщение.
Итак, алгоритм расчета площади любой фигуры методом Монте-Карло сводится к следующему:
- Фигура вписывается в прямоугольник. Координаты сторон прямоугольника известны, значит, известна его площадь.
- Псевдослучайным образом внутри прямоугольника генерируется большое количество точек. Для каждой точки определяется, попала ли точка внутрь исходной фигуры или нет.
- В результате площадь исходной фигуры вычисляется исходя из обычной пропорции: отношение количества точек, попавших в фигуру, к общему количеству сгенерированных точек равно отношению площади фигуры к площади ограничивающего ее прямоугольника.
Последняя проблема, которую надо решить, заключается в том, что каким-то образом необходимо определять, попала ли точка внутрь исходной фигуры. В моем случае данная задача решается достаточно просто, поскольку моя фигура состоит из окружностей, координаты центров и радиусы которых известны.
Реализация задачи на JavaScript
Пара гвоздей в метод Бутстрапа
Если говорить именно о методе Бутстрапа, то мое личное мнение заключается в том, что случайная генерация набора данных по имеющемуся набору в общем случае не может служить для оценки закономерностей, поскольку сгенерированная информация не является достоверной. В общем, это же, только более умными (и нередко более резкими) словами, говорят и многие авторы, например, Орлов в своем учебнике по Эконометрике.
[spoiler title=”источники:”]
http://abakbot.ru/online-2/73
http://habr.com/ru/post/192272/
[/spoiler]
| Радиус первой окружности |
| Радиус второй окружности |
| Расстояние между двумя окружностями |
| Площадь пересечения двух окружностей по заданным параметрам равна: |
|
| Первые координаты пересечения | |
| Вторые координаты пересечения |
Позволяет рассчитать площадь пересечения двух окружностей произвольных радиусов.
Используются достаточно простые формулы, которые элементарно доказываются.
Дополнительно есть калькулятор, который высчитывает координаты пересечения двух окружностей
Площадь пересечения двух окружностей состоит из двух сегментов FDG и FBG
Вывести формулу расчета площади пересечения двух окружностей можно из двух общеизвестных формул и знаний решения треугольника:
Формулы сектора окружности
(S=cfrac{alpha(R^2)}{2})
и длина хорды окружности
(L=2Rsin(cfrac{alpha}{2}))
По известным сторонам треугольника AFС определяем высоту на сторону AC.
Удвоением этой высоты мы получаем длину хорды, после этого узнаем угол альфа по второй формуле.
По известным сторонам треугольника AFG узнаем его площадь. Вычитаем её из площади сектора окружности, ведь угол альфа нам уже известен.
И получаем площадь сегмента FBG
Подобным образом вычисляем FDG
Это лишь один из способов решения задачи вычисления площади пересечения двух окружностей.
(S=S_1+S_2)
(S_1=cfrac{R_1^2*(F_1-sin(F_1))}{2})
(S_2=cfrac{R_2^2*(F_2-sin(F_2))}{2})
где
(F_1=2*acos{cfrac{R_1^2-R_2^2+D^2}{2*R_1*D}})
(F_2=2*acos{cfrac{R_2^2-R_1^2+D^2}{2*R_2*D}})
где
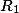 – радиус первой окружности
– радиус первой окружности
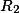 – радиус второй окружности
– радиус второй окружности
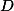 – расстояние между центрами окружностей
– расстояние между центрами окружностей
Пример
Хотим узнать площадь пересечения двух окружностей радиусом в 1 и расстоянием между центрами 0.8079455
Пишем okr 1 1 0.8079455
Ответ
Площадь двух пересекающихся окружностей равна = 1.5707963388681~ (pi/2)
Первая окружность радиус 4, вторая окружность радиус 2, расстоянием между центрами 3
Пишем okr 4 2 3
Ответ
Площадь двух пересекающихся окружностей равна = 9.5701994729833
Первая окружность радиус 4, вторая окружность радиус 2, расстоянием между центрами 0
Пишем okr 4 2 0
Ответ
Окружности не пересекаются
геометрия — Как найти площадь пересечения прямоугольников?
Есть 2 прямоугольника, как найти площадь их пересечения? Стороны прямоугольников паралельны осям.
задан 12 Янв ’12 17:00
Эта задача для какого класса?
А в чем разница?
1 ответ
Кхм. Очень просто. Пусть прямоугольник $%A$% ограничен координатами $%(X_, Y_, X_, Y_)$%, а прямоугольник $%B$% — координатами $%(X_, Y_, X_, Y_)$%, где Л — лево, П — право, Н — низ, В — верх.
Алгоритм нахождения площади пересечения
Вот задача, но мне не нужен код, помогите с алгоритмом нахождения площади пересечения.
Напишите программу, которая находит площадь пересечения, то есть общей части двух прямоугольников. Каждый прямоугольник задается координатами двух произвольных противоположных углов. Стороны прямоугольников параллельны осям координат.
Ваша программа должна вводить с клавиатуры числа x1, y1, x2, y2, x3, y3, x4, y4. Числа xi, yi будут вводиться в i-строке (1≤i≤4) и разделяться одним пробелом. Точки (x1, y1) и (x2, y2) – координаты двух противоположных углов первого прямоугольника. Точки (x3, y3) и (x4, y4) – координаты двух противоположных углов второго прямоугольника.
Числа xi, yi – целые; 0≤xi, yi≤30000; оба прямоугольника имеют ненулевую площадь.
Ваша программа должна вывести на экран одно число S – площадь общей части двух введенных прямоугольников. Если введенные прямоугольники не имеют общих точек, то ваша программа должна вывести на экран число 0.
собственно, всё сводится к нахождению пересечений отрезков (x1, x2) ∩ (x3, x4) и отрезков (y1,y2) ∩ (y3, y4)
а пересечение отрезков (a, b)∩(c, d) посчитать легко: это (max(a,c), min(b,d)).
если max(a,c) > min(b,d), то пересечение пустое
так что программа простая:
1) приводишь прямоугольники (xi, yi) — (xj, yj) к «нормальному» виду
xi < xj, yi < yj
2) находишь пересечения отрезков
(x1, x2) ∩ (x3, x4) = (xA, xB)
(y1, y2) ∩ (y3, y4) = (yA, yB)
3) если пересечения не пустые, считаешь площадь прямоугольника (xA, yA) — (xB, yB)
Задача по Python 3.6?
На плоскости даны два прямоугольника, каждый прямоугольник задан координатами левого нижнего и правого верхнего угла. Найдите площадь пересечения этих прямоугольников.
ВХОДНЫЕ ДАННЫЕ
Программа получает на вход 8 чисел. Сначала даны координаты левого нижнего угла первого прямоугольника . Затем даны координаты правого верхнего угла первого прямоугольника . Затем аналогично даны координаты второго прямоугольника и .
Числа заданы по одному числу в строке, −10000⩽x1
ВЫХОДНЫЕ ДАННЫЕ
Программа должна выводить одно целое число – площадь пересечения данных прямоугольников.
- Вопрос задан более двух лет назад
- 988 просмотров
- Вконтакте
x1=int(input())
y1=int(input())
x2=int(input())
y2=int(input())
x3=int(input())
y3=int(input())
x4=int(input())
y4=int(input())
# границы области пересечения
left = max(x1, x3) # левая
bottom = max(y1, y3) # нижняя
right = min(x2, x4) # правая
top = min(y2, y4) # верхняя
width = right — left # ширина пересечения
height = top — bottom # высота пересечения
# если ширина и высота области пересечения меньше или равны 0
if width <= 0 or height <= 0:
# то его площадь 0
—-print(0)
else:
# если больше 0, то выводим площадь
—-print(width * height)
Добрый день, участники форума.
Подскажите, пожалуйста.
Дано:
На карте имеем два магазина с одинаковыми зонами (1 км радиусами поражения) – две окружности.
Точно известно, что эти две окружности пересекаются.
Известны координаты каждого магазина.
Вопрос:
1) Какова формулу для расчета процента пересечения = площади зоны пересечения двух окружностей/площадь окружности первого магазина?
2) Формулы расчета площади пересечения двух окружностей достаточно сложны. Возможно ли воспользоваться тем, что заранее известно, что радиусы всегда одинаковые, и существенно упростить формулу расчета?
Например, мы просто:
– рассчитали ту часть радиуса, который находится в зоне пересечения (2R минус расстояние между точками)
– поделили полученную цифру на 2R
Получилась цифра процента пересечения почти удовлетворительной точности. Условно, подобный расчет предполагает как будто пересекаются не окружности, а квадраты. Поэтому начинает сильно ошибаться в сторону увеличения, когда зоны пересечения малы. Например визуально видно, что зоны пересекаются процентов на 5, а расчет показывает 20%.
Можно ли как-то уточнить формулу, не слишком усложняя алгоритм расчета, по крайней мере таким образом, чтобы его можно было посчитать в экселе.
|
Чему равна площадь пересечения двух треугольников, если (см)?Winiki 2 месяца назад
В прямоугольник ABCD вписаны два треугольника – ∆AED и ∆BFA. При этом нам абсолютно случайно стали известны значения площадей для трёх фигур:
Задача: Чему равна площадь пересечения двух треугольников ∆AED и ∆BFA? Sahgi = ? P.S. Не забывайте, что короткие ответы вредят самочувствию вашего аккаунта! Знаете ответ? |
|
Есть интересный вопрос? Задайте его нашему сообществу, у нас наверняка найдется ответ! |
Делитесь опытом и знаниями, зарабатывайте награды и репутацию, заводите новых интересных друзей! |
Задавайте интересные вопросы, давайте качественные ответы и зарабатывайте деньги. Подробнее.. |
Статистика проекта за месяц
Новых пользователей: 4429
Создано вопросов: 16333
Написано ответов: 37952
Начислено баллов репутации: 897908