Материал из Решебника
Информация о задаче
Задача №2473 параграфа №1 главы №8 “Применения интеграла” книги Г.Н. Бермана “Сборник задач по курсу математического анализа” (22-е издание, 2002 год).
Условие задачи
Найти площадь петли линии [math]y^2=x(x-1)^2[/math].
Решение
Так как [math]y^2ge{0}[/math], то [math]x(x-1)^2ge{0}[/math], что равносильно [math]xge{0}[/math]. При условии [math]xge{0}[/math] получим две ветви заданного графика:
[dmath]
|y|=sqrt{x}cdot|x-1|;;
left[begin{aligned}
&y=-sqrt{x}cdot|x-1|;\
&y=sqrt{x}cdot|x-1|.
end{aligned}right.
[/dmath]
Эти ветви симметричны относительно оси абсцисс, при этом каждая ветвь имеет с данной осью две общие точки: [math](0;0)[/math] и [math](1;1)[/math]. Если [math]xin(0;1)cup(1;+infty)[/math], то ветвь [math]y=-sqrt{x}cdot|x-1|[/math] расположена под осью Ox, а ветвь [math]y=sqrt{x}cdot|x-1|[/math] – над данной осью.
Рассматриваемые ветви образуют петлю при [math]xin[0;1][/math]. Так как ветви симметричны относительно оси абсцисс, то искомая площадь [math]S=2S_1[/math], где [math]S_1[/math] – площадь между ветвью [math]y=sqrt{x}cdot|x-1|[/math] и осью Ox.
[dmath]
S=2intlimits_{0}^{1}left(sqrt{x}cdot|x-1|right)dx
=2intlimits_{0}^{1}left(sqrt{x}cdot(1-x)right)dx
=2intlimits_{0}^{1}left(x^{1/2}-x^{3/2}right)dx
=4cdotleft.left(frac{x^{3/2}}{3}-frac{x^{5/2}}{5}right)right|_{0}^{1}
=frac{8}{15}.
[/dmath]
Ответ
[math]frac{8}{15}[/math]
Заметили ошибку, опечатку, или неправильно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
– 37 –
1.2 Приложения
определённого интеграла.
При решении
большинства задач на геометрические
приложения определённого интеграла,
прежде всего, надо ответить на два
вопроса:
1) Какая формула
соответствует Вашей задаче? 2) Каковы
пределы интегрирования в определённом
интеграле, который даёт искомый результат?
Чтобы ответить на эти вопросы необходимы
рисунки линий из условий задачи, причем
речь не идёт о точных графиках, а лишь
о взаимном расположении линий и о точках
их пересечений.
Задача
1. Вычислить
площадь фигуры, ограниченной петлёй
линии
Решение.
Уравнение (неявное) линии не изменяется
при замене
на
,
следовательно, линия симметрична
относительно оси абсцисс. Часть линии,
которая лежит в верхней полуплоскости,
является графиком функции
Заметим, что по
умолчанию все параметры считаются
положительными. Область определения
этой функции:
Её график пересекает
ось абсцисс в точках
и при
Вся линия имеет
вид
Заштрихованная
фигура является криволинейной трапецией.
Базовая формула для вычисления площади
такой фигуры:
.
В нашей задаче
искомая площадь (учитывая симметрию):
Задача
2. Найти
площадь фигуры, ограниченной графиками
функций:
и
и прямой
.
Решение.
Для построения эскиза фигуры достаточно
заметить следующее:
-
функция
четная,
а
нечетная, следовательно, график
симметричен относительно оси ординат,
а
относительно начала координат; -
-
Обе функции
положительны при
и стремятся к нулю при
;
-
Равенство
имеет место лишь в точке
Такой «картинке»
соответствует формула
В нашем случае
Вычисляем площадь:
Замечание
1. Линии,
указанные в условии задачи, ограничивают
ещё одну фигуру: она лежит левее оси
ординат. Однако, её площадь бесконечна,
ибо интеграл (несобственный!)
расходится: при
подынтегральная функция эквивалентна
Задача
3. Найти
площадь фигуры, ограниченной графиками
функций
и
.
Решение.
Внешне неэлементарную функцию
выразим через элементарные
Фигура имеет вид
Чтобы найти пределы
интегрирования в формуле из предыдущей
задачи, надо решить уравнение
,
которое распадается на две такие системы
и
Их решения:
Так как верхняя граница фигуры задана
двумя различными формулами, надо
воспользоваться аддитивностью
определённого интеграла. Имеем для
искомой площади:
Замечание
2. Вообще
говоря, для функции
можно получить элементарное представление.
Действительно, для функции
Элементарное
представление имеет вид
.
Сдвиги вдоль координатных осей преобразуют
в
:
Задача 4.
найти площадь фигуры, ограниченной
линиями
и
Решение.
Чтобы нарисовать линию, заданную
параметрическими уравнениями, нарисуем
(схематично) сначала графики функций
и
.
Теперь нетрудно
заметить, что линия
состоит из двух ветвей: верхняя
соответствует изменению параметра от
до
,
нижняя соответствует значениям
.
Обе ветви выходят из начала координат
которое соответствует
.
Решив систему
найдём два замечания
параметра
,
при которых ветви линии
пересекают прямую
.
Заштрихованную фигуру можно понимать
как «разность» двух криволинейных
трапеций. Формула для площади трапеции
примыкающей к оси
:
где
параметрические уравнения криволинейной
границы трапеции,
соответствует левой границе трапеции,
а
правой.
В нашей задаче
большая трапеция ограничена верхней
ветвью линии
и
,
меньшая трапеция ограничена нижней
ветвью и
.
Итак, имеем для площади:
Здесь при вычислении
интеграла мы использовали свойство
аддитивности и свойства интеграла от
четной функций по симметричному
промежутку.
Задача
5. Найти
площадь фигуры, ограниченной петлёй
линии

Решение.
Сначала изобразим линию в декартовой
системе
:
это график функций
;

это график функций

Прямые
вертикальные
асимптоты.
Чтобы построить
в полярной системе координат точку
с координатами
,
проводим луч
с началом в полюсе
и по этому лучу откладываем отрезок
длиной
.
Вращая луч вокруг полюса и откладывая
по нему полярный радиус
,
соответствующий полярную углу
,
получим требуемую линию.
Декартов график
нашей функции показывает, что с увеличением
угла
от
до
полярный радиус
увеличивается, то есть точка удаляется
от полюса в бесконечность. Вертикальная
асимптота
этого графика означает, что в полярной
системе линия не пересекает луч
.
Если теперь изменять
в отрицательном направлении(т.е. вращать
луч по часовой стрелке), то в силу четности
косинуса получим симметричную относительно
полярной оси ветвь линии.
Значениям
и
соответствует одна и та же точка линии
– точка самопересечения. Таким образом,
петля линии соответствует изменению
от
до
.
Вычислим площадь верхней части фигуры.
Она представляет собой криволинейный
сектор, площадь которого вычисляется
по формуле
.
В нашем случае
.
С учётом симметрии получим для площади:
Замечание
3. пусть
полярная и декартова системы координат
совместимы обычным образом. Формулы
связи декартовых координат
с полярными
:
Если
текущая точка данной линии, то можно
показать, что при
Это означает, что
прямая
– это асимптота линии при
.
То же самое можно сказать и о прямой.
.
Задача
6. Найти
длину графика функции
.
Решение. Формула
длины линии(или её части), заданной явно
,
имеет вид
В нашем случае
и
– граничные точки области определения
данной функции
определена на отдельных отрезках вида
,
на которых
.
Однако, проинтегрировать эту функцию
по отрезку
можно лишь для
.
Имеем для нашей задачи:
(теорема
Барроу),
,
Задача
7. вычислить
длину внешней части линии
.
Решение.
Как и в задаче 5, рассмотрим сначала
график данной функции в декартовой
системе координат.
График функции
– это синусоида, растянутая вдоль оси
.
Возведение синуса в куб не изменяет
промежутки возрастания и убывания,
экстремумы и нули.
В полярной системе
координат линия имеет следующий вид.
При
полярный радиус
,
т.е. точка линии находится в полюсе. При
увеличении
(при
вращении луча против часовой стрелке)
возрастает, т.е. точка линии удаляется
от полюса. Максимальное удаление линия
имеет при
.
При дальнейшем увеличении
до
точка вернётся в полюс, причем по
симметричной ветви линии. Точка
самопересечения соответствует значениям
и
.
Внешняя часть линии соответствует
.
Формула для
вычисления длины линии
:
Предварительные
вычисления:
Имеем для искомой
длины:

Задача
8. найти
прямую
,
которая делит каждую арку циклоиды
на части, длины
которых относятся как
.
Решение.
Длина дуги линии заданной параметрическими
уравнениями
вычисляется по формуле
Так как арки
циклоиды одинаковые, будем рассматривать
первую из них, которая соответствует
значениям параметра
.
Предварительные вычисления:
— это подынтегральная
функция в формуле для вычисления длины
части циклоиды. Вообще говоря,
,
но
,
значит
Прямая
,
делит эту арку циклоиды на 3 части. Две
части, лежащие ниже прямой имеют
одинаковые длины, ибо арка симметрично
относительно прямой
,
проходящей через вершину арки. По условию
задачи суммарная длина этих двух частей
равна длине части, которая лежит выше
прямой
.
Чтобы ответить на вопрос задачи, надо
найти значение параметра
такое, что

Если вычислить
эти интегралы, то придем к уравнению
При
условии
это уравнение имеет один корень
.
Для этого значения параметра
.
Итак, искомая прямая имеет уравнение
.
Задача
9. фигура,
ограниченная осью
и одной волной синусоиды
вращается вокруг: а) оси
;
б) оси
.
Найти объёмы получающихся тел вращения.
Решение.
Если стандартную трапецию, ограниченную
графиком
и прямыми
,
вращать вокруг оси
или оси
,
то получим тела, объёмы которых вычисляются
по формулам:
,
.
Волна синусоиды
состоит из двух полуволн, которые при
вращении дают равновеликие тела. При
вращении вокруг
объём тела не зависит от того, какую из
полуволн (или волн) вращаем. Напротив,
для вращения вокруг
это
существенно. Для определённости
рассмотрим первую полуволну, которая
соответствует изменению
от
до
.
Имеем для искомых объёмов:
Задача
10. Фигура,
ограниченная петлёй линии
вращается вокруг: а) оси
;
б) оси
.
Найти объёмы получающихся тел вращения.
Решение.
Графики функций
и
Сочетание четности
функции
и нечетности функции
означает симметрию линии
относительно оси
.
Поэтому достаточно рассматривать
.
Значению параметра
соответствует точка
.
Для значений
соответствующая часть линии
лежит ниже оси
,
а для
выше оси. Значению
соответствует точка
.
Эта же точка соответствует и
:
точка
это точка самопересечения линии
.
Заштрихованная
часть петли – это криволинейная трапеция,
причем меньшему значению абсциссы
соответствует
,
а большему
– значение
.
Для вычисления
объёмов можно использовать формулы из
предыдущей задачи, заменив
на
,
на
и
:
,
.
Имеем для искомых
объёмов:
Коэффициент 2 в
последней формуле учитывает симметрию
фигуры при вращении вокруг
.
Замечание
4. в данной
задаче, пункт а), фигура вращения вокруг
прямой, которая пересекает её. В общем
случае это недопустимо. Однако, в нашем
случае ось вращения – это ось симметрии
фигуры и две половинки фигуры дают одно
и то же тело вращения. Это же замечание
относится к задачам 12 и 13.
Задача
11.
Полуокружность
вращается вокруг той касательной,
которая параллельна диаметру. Найти
площадь получающейся поверхности.
Решение.
Пусть центр окружности лежит на оси
ординат, а касательная – это ось абсцисс.
Уравнение такой окружности
.
Явное уравнение нижней полуокружности
Общая формула для
вычисления площади поверхности вращения
где
ордината текущей точки линии, которая
вращается,
подынтегральное выражение в формуле
для вычисления длины линии. В случае
явного задания линии
,
,
эта формула принимает вид:
Предварительные
вычисления:
Вычисляем площадь:
Соседние файлы в папке RGR 3
- #
- #
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Merhaba |
Заголовок сообщения: Площадь петли линии
|
||
|
Добрый вечер!!!
|
||
| Вернуться к началу |
|
||
|
Merhaba |
Заголовок сообщения: Re: Площадь петли линии
|
|
pewpimkin
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Площадь петли линии
в форуме Интегральное исчисление |
LegG |
6 |
230 |
09 сен 2020, 21:24 |
|
Найти площадь петли линии
в форуме Интегральное исчисление |
ruslan95 |
1 |
1596 |
03 май 2014, 14:12 |
|
Найти площадь петли кривой
в форуме Maple |
dddsss |
5 |
684 |
24 мар 2019, 15:51 |
|
Петли в псевдографе
в форуме Дискретная математика, Теория множеств и Логика |
Piteryo |
0 |
238 |
19 мар 2016, 12:28 |
|
Найти длину петли
в форуме Интегральное исчисление |
LonelyGamer |
1 |
405 |
03 апр 2016, 16:22 |
|
Найти длину дуги петли
в форуме Интегральное исчисление |
md_house |
2 |
581 |
10 май 2018, 15:17 |
|
Найти площадь площадь ограниченной линиям
в форуме Интегральное исчисление |
bibibo |
3 |
659 |
15 апр 2014, 19:33 |
|
Линии
в форуме Аналитическая геометрия и Векторная алгебра |
FCJUVENTUS |
1 |
362 |
02 ноя 2013, 12:59 |
|
Линии
в форуме Аналитическая геометрия и Векторная алгебра |
russian89nur |
1 |
585 |
10 ноя 2014, 23:42 |
|
Векторные линии
в форуме Векторный анализ и Теория поля |
Sykes |
3 |
234 |
14 апр 2021, 13:10 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 5 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Уравнение петли в параметрическом виде
Построим график параметрической функции x=x(t) и y=y(t), которая задаёт прямую или кривую линию,
где параметр t лежит в промежутке [a, b],
и вы можете указать свои границы.
Задайте также функции x и y, зависящих от параметра.
Примеры кривых
| Название кривой | Уравнение |
|---|---|
| Окружность | |
| Спираль | |
| Дельтоида | |
| Астроида | |
| Гипоциклоиды | |
| Кардиоида | |
| Нефроида | |
| Эпициклоиды | |
| Бабочка | |
| Фигуры Лиссажу | |
| Сердце |
Правила ввода выражений и функций
3.14159.. e Число e – основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности – знак для бесконечности
© Контрольная работа РУ – калькуляторы онлайн
Где учитесь?
Для правильного составления решения, укажите:
Вычисление площади фигуры, ограниченной параметрически заданной кривой
Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x = a , x = b , а также непрерывной (неотрицательной или неположительной) функцией y = f ( x ) . Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t . В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.
После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.
Основная формула для вычисления
Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x = a , x = b , ось O x и параметрически заданная кривая x = φ ( t ) y = ψ ( t ) , а функции x = φ ( t ) и y = ψ ( t ) являются непрерывными на интервале α ; β , α β , x = φ ( t ) будет непрерывно возрастать на нем и φ ( α ) = a , φ ( β ) = b .
Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S ( G ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t .
Мы вывели ее из формулы площади криволинейной трапеции S ( G ) = ∫ a b f ( x ) d x методом подстановки x = φ ( t ) y = ψ ( t ) :
S ( G ) = ∫ a b f ( x ) d x = ∫ α β ψ ( t ) d ( φ ( t ) ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t
Учитывая монотонное убывание функции x = φ ( t ) на интервале β ; α , β α , нужная формула принимает вид S ( G ) = – ∫ β α ψ ( t ) · φ ‘ ( t ) d t .
Если функция x = φ ( t ) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.
Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой
В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.
Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x = 2 cos t y = 3 sin t .
Решение
У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3 . См на иллюстрацию:
Попробуем найти площадь 1 4 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x ∈ a ; b = 0 ; 2 . Далее умножим полученное значение на 4 и найдем площадь целой фигуры.
Вот ход наших вычислений:
x = φ ( t ) = 2 cos t y = ψ ( t ) = 3 sin t φ α = a ⇔ 2 cos α = 0 ⇔ α = π 2 + πk , k ∈ Z , φ β = b ⇔ 2 cos β = 2 ⇔ β = 2 πk , k ∈ Z
При k , равном 0 , мы получим интервал β ; α = 0 ; π 2 . Функция x = φ ( t ) = 2 cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:
– ∫ 0 π 2 3 sin t · 2 cos t ‘ d t = 6 ∫ 0 π 2 sin 2 t d t = 3 ∫ 0 π 2 ( 1 – cos ( 2 t ) d t = = 3 · t – sin ( 2 t ) 2 0 π 2 = 3 · π 2 – sin 2 · π 2 2 – 0 – sin 2 · 0 2 = 3 π 2
Значит, площадь фигуры, заданной исходной кривой, будет равна S ( G ) = 4 · 3 π 2 = 6 π .
Ответ: S ( G ) = 6 π
Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале x ∈ a ; b = – 2 ; 2 . В этом случае у нас бы получилось:
φ ( α ) = a ⇔ 2 cos α = – 2 ⇔ α = π + π k , k ∈ Z , φ ( β ) = b ⇔ 2 cos β = 2 ⇔ β = 2 π k , k ∈ Z
Таким образом, при k равном 0 , мы получили β ; α = 0 ; π . Функция x = φ ( t ) = 2 cos t на этом интервале будет монотонно убывать.
После этого вычисляем площадь половины эллипса:
– ∫ 0 π 3 sin t · 2 cos t ‘ d t = 6 ∫ 0 π sin 2 t d t = 3 ∫ 0 π ( 1 – cos ( 2 t ) d t = = 3 · t – sin ( 2 t ) 2 0 π = 3 · π – sin 2 · π 2 – 0 – sin 2 · 0 2 = 3 π
Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.
Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x = a · cos t y = b · sin t . Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса S э л и п с а = πab .
Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x = R · cos t y = R · sin t , где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R : S к р у г а = πR 2 .
Разберем еще одну задачу.
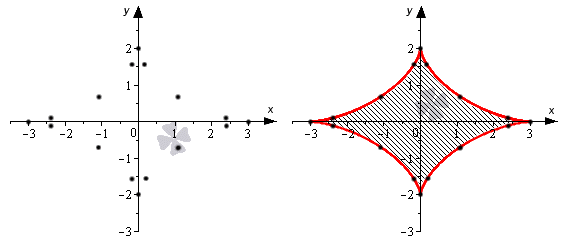
Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x = 3 cos 3 t y = 2 sin 3 t .
Решение
Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x = a · cos 3 t y = a · sin 3 t .
Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.
У нас x = φ ( t ) = 3 cos 3 t , y = ψ ( t ) = 2 sin 3 t .
Данные функции являются определенными для всех действительных значений t . Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x = φ ( t ) = 3 cos 3 t , y = ψ ( t ) = 2 sin 3 t для некоторых t = t 0 ∈ 0 ; 2 π π 8 , π 4 , 3 π 8 , π 2 , . . . , 15 π 8 , получим точки x 0 ; y 0 = ( φ ( t 0 ) ; ψ ( t 0 ) ) .
Составим таблицу итоговых значений:
| t 0 | 0 | π 8 | π 4 | 3 π 8 | π 2 | 5 π 8 | 3 π 4 | 7 π 8 | π |
| x 0 = φ ( t 0 ) | 3 | 2 . 36 | 1 . 06 | 0 . 16 | 0 | – 0 . 16 | – 1 . 06 | – 2 . 36 | – 3 |
| y 0 = ψ ( t 0 ) | 0 | 0 . 11 | 0 . 70 | 1 . 57 | 2 | 1 . 57 | 0 . 70 | 0 . 11 | 0 |
| t 0 | 9 π 8 | 5 π 4 | 11 π 8 | 3 π 2 | 13 π 8 | 7 π 4 | 15 π 8 | 2 π |
| x 0 = φ ( t 0 ) | – 2 . 36 | – 1 . 06 | – 0 . 16 | 0 | 0 . 16 | 1 . 06 | 2 . 36 | 3 |
| y 0 = ψ ( t 0 ) | – 0 . 11 | – 0 . 70 | – 1 . 57 | – 2 | – 1 . 57 | – 0 . 70 | – 0 . 11 | 0 |
После этого отметим нужные точки на плоскости и соединим их одной линией.
Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x ∈ a ; b = 0 ; 3 :
φ ( α ) = a ⇔ 3 cos 3 t = 0 ⇔ α = π 2 + πk , k ∈ Z , φ ( β ) = b ⇔ 3 cos 3 t = 3 ⇔ β = 2 πk , k ∈ Z
Если k равен 0 , то у нас получится интервал β ; α = 0 ; π 2 , и функция x = φ ( t ) = 3 cos 3 t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:
– ∫ 0 π 2 2 sin 3 t · 3 cos 3 t ‘ d t = 18 ∫ 0 π 2 sin 4 t · cos 2 t d t = = 18 ∫ 0 π 2 sin 4 t · ( 1 – sin 2 t ) d t = 18 ∫ 0 π 2 sin 4 t d t – ∫ 0 π 2 sin 6 t d t
У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу J n ( x ) = – cos x · sin n – 1 ( x ) n + n – 1 n J n – 2 ( x ) , где J n ( x ) = ∫ sin n x d x .
∫ sin 4 t d t = – cos t · sin 3 t 4 + 3 4 ∫ sin 2 t d t = = – cos t · sin 3 t 4 + 3 4 – cos t · sin t 2 + 1 2 ∫ sin 0 t d t = = – cos t · sin 3 t 4 – 3 cos t · sin t 8 + 3 8 t + C ⇒ ∫ 0 π 2 sin 4 t d t = – cos t · sin 3 t 4 – 3 cos t · sin t 8 + 3 8 t 0 π 2 = 3 π 16 ∫ sin 6 t d t = – cos t · sin 5 t 6 + 5 6 ∫ sin 4 t d t ⇒ ∫ 0 π 2 sin 6 t d t = – cos t · sin 5 t 6 0 π 2 + 5 6 ∫ 0 π 2 sin 4 t d t = 5 6 · 3 π 16 = 15 π 96
Мы вычислили площадь четверти фигуры. Она равна 18 ∫ 0 π 2 sin 4 t d t – ∫ 0 π 2 sin 6 t d t = 18 3 π 16 – 15 π 96 = 9 π 16 .
Если мы умножим это значение на 4 , получим площадь всей фигуры – 9 π 4 .
Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x = a · cos 3 t y = a · sin 3 t , можно найти по формуле S а с т р о и д ы = 3 πa 2 8 , а площадь фигуры, которая ограничена линией x = a · cos 3 t y = b · sin 3 t , считается по формуле S = 3 πab 8 .
Уравнение петли в параметрическом виде
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/vychislenie-ploschadi-figury-ogranichennoj-paramet/
http://yukhym.com/ru/integrirovanie-funktsii/ploshchad-figury-ogranichennoj-parametricheskimi-krivymi.html
[/spoiler]
кто умеет рисовать график петли кривой, заданной параметрически объясните плииз как?
Rav
Знаток
(268),
закрыт
14 лет назад
x=t^2 – 4
y=t^3 – 4t
и если не трудно найдите площадь) я сам решил, просто сверить ответы…
спасибо!
Адмирал Худ
Гуру
(2807)
14 лет назад
Берёте t=0, 1, 2 …и для каждого значения вычисляете по указанным формулам x и y. Точки с этими координатами строите на листочке в клеточку и соединяете плавной линией.
Можно по другому. Избавиться от параметрического задания, привести к уравнению y=f(х) :
x = t²–4 => t = √(x+4)
y = t³–4t => y = √(x+4)³ – 4√(x+4)
Последний график строим как обычно.
Площадь не могу определить, фигура не замкнутая.