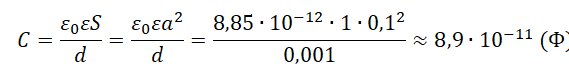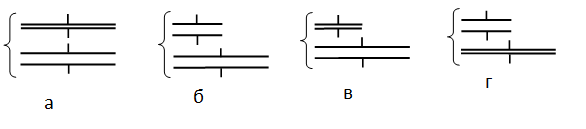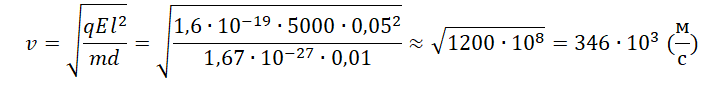Перейти к контенту
Условие задачи:
Определить площадь пластин плоского воздушного конденсатора электроемкостью 1 мкФ, если расстояние между пластинами 1 мм.
Задача №6.4.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(C=1) мкФ, (d=1) мм, (S-?)
Решение задачи:
Электроемкость плоского конденсатора определяется по следующей известной формуле:
[C = frac{{varepsilon {varepsilon _0}S}}{d}]
Выразим из этой формулы искомую площадь пластин конденсатора (S):
[S = frac{{Cd}}{{varepsilon {varepsilon _0}}}]
Задача решена в общем виде, остается только произвести расчет. Напомним, что электрическая постоянная (varepsilon _0) равна 8,85·10-12 Ф/м, диэлектрическая проницаемость воздуха (varepsilon) равна 1. Не забывайте переводить численные значения величин в систему СИ.
[S = frac{{{{10}^{ – 6}} cdot {{10}^{ – 3}}}}{{1 cdot 8,85 cdot {{10}^{ – 12}}}} = 113;м^2]
Мы получили какое-то огромное число, тем не менее в ответах в конце сборника указан такой же ответ.
Ответ: 113 м2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.4.9 Плоский воздушный конденсатор состоит из двух пластин площадью 100 см2 каждая
6.4.11 Плоский конденсатор составлен из двух круглых пластин диаметром 0,54 м каждая
6.4.12 Плоский воздушный конденсатор погрузили в керосин. Во сколько раз изменилась
( 9 оценок, среднее 4.56 из 5 )
Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.
Плоский конденсатор — система двух разноименно заряженных пластин.
Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:
U=Ed
Электроемкость конденсатора
Определение
Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.
Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).
Электроемкость конденсатора определяется формулой:
C=ε0εSd
- ε0 — диэлектрическая постоянная, равная 8,85∙10–12 Кл2/(Н∙м2);
- ε — диэлектрическая проницаемость среды;
- S (м2) — площадь каждой пластины.
Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.
Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:
C=QU=qU
Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.
Энергия конденсатора
Формула энергии конденсатора
Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:
Wэ=q22C=CU22
Подсказки к задачам
| Конденсатор отключен от источника | q = q′ |
| Конденсатор подключен к источнику | U = U′ |
| Количество теплоты и энергия конденсатора | Q = ∆Wэ |
Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.
10 см = 0,1 м
1 мм = 0,001 м
Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.
Площадь квадратной пластины равна квадрату ее стороны:
S = a2
Соединения конденсаторов
| Последовательное соединение | Параллельное соединение | |
| Схема | 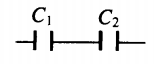 |
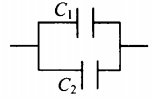 |
| Напряжение |
U=U1+U2 |
U=U1=U2 |
| Заряд |
q=q1=q2 |
q=q1+q2 |
| Электроемкость |
1C=1C1+1C2 |
C=C1+C2 |
Подсказки к задачам
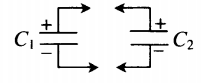
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами. | Схема соединения конденсаторов одноименными полюсами:
Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
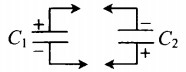
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами. |
Схема соединения конденсаторов разноименными полюсами: Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
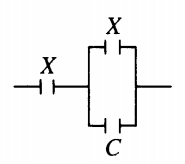
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.
Электрическая емкость параллельного соединения равна:
Cпарал=X+C
Электроемкость последовательного соединения:
1Cпослед=1Cпарал+1X=1X+C+1X
Учтем, что суммарная электроемкость равна C:
1C=1X+C+1X
Преобразуем, умножим выражение на CX(X+C):
X(X+C)=CX+C(X+C)
Раскроем скобки:
X2+XC=CX+CX+C2
X2−CX−C2=0
Решив уравнение, получим: X = 25,9 пФ.
Разбор задач на тему «Заряженная частица в поле конденсатора»
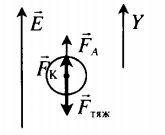
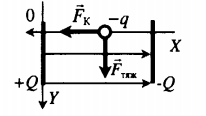
| Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U? | Условие равновесия исходит из второго закона Ньютона:
−Fтяж+−FK+−FA=0 ρш > ρ, поэтому −Fтяж> −FA. В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так: Проекция второго закона Ньютона на ось ОУ: FK+FA=Fтяж Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: Fтяж=ρш43πr3g Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: FА=ρ43πr3g Сила Кулона: FK=qUd qUd+ρ43πr3g=ρш43πr3g q=(ρш43πr3g−ρ43πr3g)dU=4πr3gd(ρш−ρ)3U |
| Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l? | 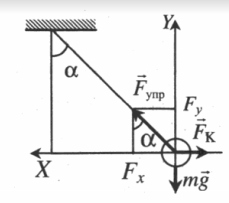
Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−Fупр=0 Проекции на оси ОХ и ОУ соответственно: Fупрsinα−FK=0 Fупрcosα−mg=0 Отсюда: kΔlsinα=qUd kΔlcosα=mg Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: (kΔl)2sin2α+(kΔl)2cos2α=(qUd)2+(mg)2 (kΔl)2(sin2α+cos2α)=(qUd)2+(mg)2 sin2α+cos2α=1 (kΔl)2=(qUd)2+(mg)2 U=dq√(kΔl)2−(mg)2 |
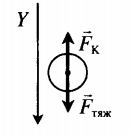
| Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=0 Проекция на вертикальную ось: Fтяж−FK=0 Fтяж=mg FK=qUd mg=qUd d=qUmg |
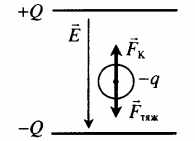
| Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью −E, направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли? | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок: Если Fтяж > FK, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: a=mg−qEm s=b Если Fтяж < FK, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: a=qE−mgm s=d Начальная скорость шарика равна нулю. Поэтому перемещение также равно: s=at22 Сделаем вычисления для случая Fтяж > FK: at22=b mg−qEmt22=b t=√2bmmg−qE Выполняя вычисления для случая Сделаем вычисления для случая Fтяж < FK, получим: t=√2bmqE−mg |
| Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого −E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Если сила Кулона направлена вправо, то sx = d. Если сила Кулона направлена вправо, то sx = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: ax=qEm ay=g Проекции перемещений на эти же оси: sx=axt22 sx=Δh=gt22 axt22=b Или: qEmt22=b Так как время движения шарика по вертикали и горизонтали одинаково: t2=2Δhg=2mbqE Δh=mbgqE |
Задание EF17979
Введите ответ в поле ввода
Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?
Для каждой величины определите соответствующий характер изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.
2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.
3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.
Решение
Емкость конденсатора определяется формулой:
C=ε0εSd
Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.
Вот как взаимосвязана электроемкость и заряд конденсатора:
C=qU
Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.
С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.
Ответ: 113
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18574
Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.
Алгоритм решения
1.Проанализировать каждый этап эксперимента.
2.Установить, от чего зависит угол отклонения стрелки электрометра.
3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.
Решение
На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.
На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:
C=ε0εSd
S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.
Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.
На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:
C=qU
Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.
Ответ: Увеличатся
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18695
Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?
Алгоритм решения
- Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
- Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.
Решение
Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18703
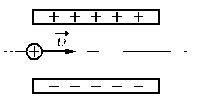
Ответ записать в км/с, округлив до десятков.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.
3.Выяснить, при каком условии протон успеет вылететь из конденсатора.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса протона: m = 1,67∙10–27 кг.
• Заряд протона: q = 1,6∙10–19 Кл.
• Расстояние между обкладками конденсатора: d = 1 см.
• Длина пластин конденсатора: l = 5 см.
• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.
1 см = 0,01 м
5 см = 0,05 м
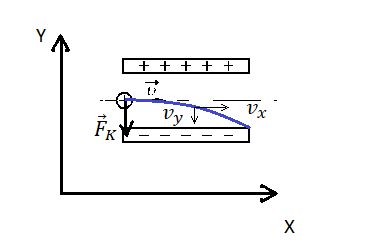
Сделаем рисунок:
Изначально протон обладает только горизонтальной скоростью v, равной vx. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.
Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью vx:
t=lvx=lv
Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):
0,5d=at22
Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:
t=√da
Приравняем правые части уравнений времени и получим:
lv=√da
Отсюда скорость равна:
v=√al2d
Ускорение выразим из второго закона Ньютона:
FK=ma=qUd
a=qUmd
Но известно, что:
U=Ed
Поэтому:
a=qEdmd=qEm
Отсюда:
Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙103 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.
Ответ: 350
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.9k
Расчёт ёмкости конденсатора
Конденсаторы нашли в наше время очень широкое применение в электронике и электротехнике, ведь они являются основными элементами большинства электрических цепей и схем. Постараемся подробно в данной статье рассказать — что такое электроемкость конденсатора. Так же будут приведены применяемые формулы расчета, описаны различные виды таких устройств и рассказано об их маркировке. Кроме того будет затронуто влияние различных факторов на емкость конденсатора.
Конденсатор
Прежде чем разобраться с тем, что такое емкость простейшего конденсатора, необходимо определиться, что из себя представляет этот электроэлемент. Конденсатором является радиоэлектронная деталь, которая может накапливать и отдавать определенную порцию электрического заряда. Состоит устройство из следующих элементов:
- Корпуса. Зачастую выполняется из алюминия. По форме он может быть плоским, сферическим и цилиндрическим.
- Обкладок (2 и более). Их делают из металлических пластинок или фольги.
- Диэлектрической прокладки. Устанавливается между обкладками и служит в качестве изолятора.
- Двух или более выводных контактов для подключения устройства в электроцепь.
Работает такой накопитель электрического заряда следующим образом.
- В момент подключения элемента к источнику электрического тока, он выступает в роли проводника. В этот момент электроток имеет максимальное значение, а напряжение — минимальное.
- На обкладках элемента начинают скапливаться положительные и отрицательные заряды (электроны и ионы). Таким образом происходит зарядка самого устройства. На момент заряда сила электротока постепенно уменьшается, а напряжение наоборот — увеличивается.
- После того как количество заряда в конденсаторе станет больше допустимого предела, он разряжается и процесс опять начинает повторяться циклически.
Основой работоспособности данного устройства является его емкость. Именно от этого параметра зависит время накопления заряда и общая «вместимость» устройства. О том, как на схемах обозначается простейший конденсатор, поможет понять следующий рисунок ниже.
Электрическая емкость, как и сами конденсаторы, нашли широкую область применения. Их используют в качестве:
- Частотных фильтров.
- Источника импульсов для различной фотоаппаратуры.
- Сглаживателей пульсирующих токов в выпрямителях.
- Фазосдвигающих элементов для электрических двигателей.
Применение конденсаторов в различных сферах основано именно на способности устройства накапливать электрический заряд. В более сложной электроаппаратуре эти устройства используются для бесперебойного поддержания определенного напряжения в разных накопителях данных.
Емкость
Емкостью конденсатора является физическая величина, которая определяет отношение между накопленным зарядом на обкладках и разностью потенциалов между ними.
В системе «СИ» емкость конденсатора и ее единица измерения — Фарад. В формулах для ее обозначения используется буква Ф (F). Однако емкость конденсатора редко измеряется в Фарадах, потому что это довольно большая величина. Чаще всего применяют ее кратные и дольные значения.
Значение электроемкости конденсатора всегда можно найти в маркировке устройства, которая нанесена на его корпус.
На схеме элемент обозначается буквой «С». Обозначение емкости является обязательным условием, ведь это позволит упростить процесс подбора необходимой электродетали для схемы.
Зависимость
Благодаря приведенному ранее описанию, мы узнали — что такое емкость. Далее попытаемся разобраться, от чего зависит эта характеристика. Емкость конденсатора зависит от расстояния между обкладками, их площади, а так же от самого материала диэлектрика. Благодаря этому можно сказать, от чего зависит емкость устройства: она прямопропорциональна площади пластины конденсатора и обратно пропорциональна расстоянию между пластинами.
Рассмотрим, как найти данную величину. Для плоского конденсатора формула расчета емкости выглядит следующим образом:
Зависимость способности устройства накапливать заряд от площади его обкладок и толщины диэлектрической прослойки так же указывает на то, что на данную величину оказывают влияние и общие размеры элемента.
Расчет
Расчет емкости конденсатора делается по довольно простой формуле:
- q — величина заряда, накопленного конденсатором.
- φ1−φ2 — разница потенциалов между его обкладками.
Данное выражение помогает довольно легко рассчитать емкость любого плоского конденсатора. Как и говорилось ранее в статье, этот величина электроёмкости конденсаторов всегда зависит от его геометрических размеров.
Плоский конденсатор
Отличительная особенность плоского конденсатора — наличие двух параллельно расположенных обкладок. Такие устройства могут иметь квадратную, круглую или прямоугольную форму.
Рассмотрим далее, как определить емкость данного вида конденсаторов. Найти емкость такого типа конденсаторов всегда поможет следующая формула:
Электроемкость
Зачастую применение конденсаторов подразумевает подключение в цепь сразу нескольких таких элементов. Благодаря этому можно увеличить общую емкость. Формула для определения электроемкости плоского конденсатора при параллельном подключении выглядит следующим образом:
Определение общей емкости для такой электроцепи делается следующим образом: C=C1+C2
Величина заряда и напряжение для такой схемы соединения определяется следующим образом:
Определить емкость конденсатора для последовательного соединения элементов позволит формула:
То есть в этом случае общую электроемкость плоского конденсатора находят с помощью выражения:
Благодаря данным выражениям найдем общее напряжение и определим величину заряда для последовательного соединения элементов:
Емкость конденсатора и применяемые формулы расчетов для различных вариантов соединения плоских устройств приведены на рисунке ниже. Можно сказать, что она очень наглядная и удобная для использования:
Сферический конденсатор
Сферическое устройство имеет две обкладки в форме концентрических сфер, между которыми расположен диэлектрик. Емкость сферического конденсатора можно определить следующим образом:
В данном выражении значение «4π» определяет коэффициент рассеивания зарядов на поверхности сферических плоскостей.
Расчет емкости сферического конденсатора можно сделать по формуле для плоского устройства в том случае, если зазор по сравнению с радиусом сферы имеет довольно маленькое значение.
Цилиндрический
Цилиндрическое устройство немного схоже с ранее описанным сферическим. В них применяются схожие по форме обкладки. Они имеют так же круглую форму, а значит на расчет емкости цилиндрического устройства так же будет влиять такой параметр, как радиус обкладок. Отличием заключается только в самой вытянутой форме пластин цилиндрического конденсатора. Емкость цилиндрического конденсатора определяется по формуле:
Сферические и цилиндрические типы элементов сильно зависимы от толщины слоя диэлектрика. Чем он толще, тем меньше будет объем заряда, а значит у него повысится устойчивость к воздействию пробивного напряжения.
Проверка
Как отмечалось ранее, емкость устройства проставляется на его корпусе. Проверить паспортную величину и имеющуюся емкость устройства можно при помощи тестера с режимом «СХ». Например, для этого подойдут популярные модели M890D, AM-1083, DT9205A, UT139C, другие. Далее надо будет:
- Выпаять и разрядить устройство. Разрядка проводится строго изолированным металлическим предметом.
- Вставить ножки конденсатора в пазы «СХ», соблюдая полярность.
- Прибор отобразит на табло результат измерений. Его нужно будет сравнить с тем, который прописан в маркировке на его корпусе. Если значения между собой сильно отличаются, то это говорит о том, что элемент неисправный и требует замены.
Если мультиметр показал наличие бесконечной емкости, то это говорит о коротком замыкании внутри корпуса устройства и оно так же признается неисправным, требующим замены. Кроме того неисправность всегда можно определить визуально по трещинам или вздутию корпуса.
Заключение
В статье было описано — что такое конденсатор, как определить его емкость, от чего зависит этот параметр и основные формулы для расчета емкости различных типов таких устройств. Устройства всегда имеют на корпусе специальную маркировку, поэтому довольно просто выбрать наиболее подходящий по значению накопитель электрозаряда. Кроме того был приведен способ проверки устройства, который позволяет определить возможные его неисправности.
Плоский конденсатор. Заряд и емкость конденсатора.
Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье мы разберемся, из чего они состоят, как работают и для чего применяются 👍 В первую очередь, рассмотрим устройство и принцип работы, а затем плавно перейдем к основным свойствам и характеристикам — заряду, энергии и, конечно же, емкости конденсатора.
Плоский конденсатор.
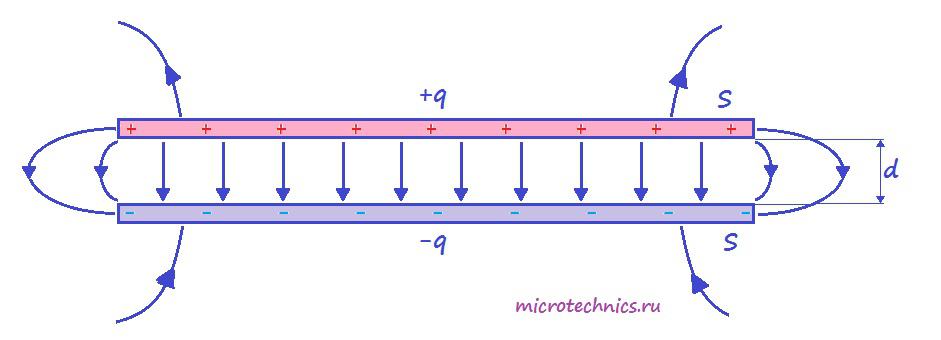
Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:
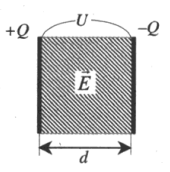
Такое устройство называется плоским конденсатором, а пластины — обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).
А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.
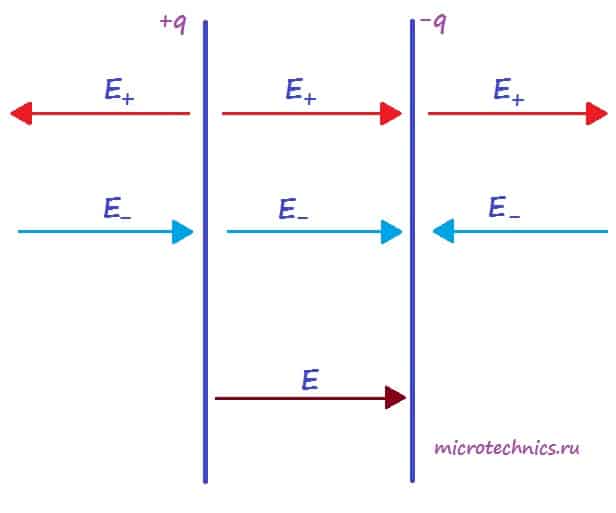
Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:
Каждая из обкладок конденсатора в отдельности создает электрическое поле:
- положительно заряженная пластина ( +q ) создает поле, напряженность которого равна E_
- отрицательно заряженная пластина ( -q ) создает поле, напряженность которого равна E_
Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:
Здесь sigma — это поверхностная плотность заряда: sigma = frac
, а varepsilon — диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:
Но направления векторов разные — внутри конденсатора вектора направлены в одну сторону, а вне — в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:
Соответственно, вне конденсатора (слева и справа от обкладок) поля пластин компенсируют друг друга и результирующая напряженность равна 0.
Процессы зарядки и разрядки конденсаторов.
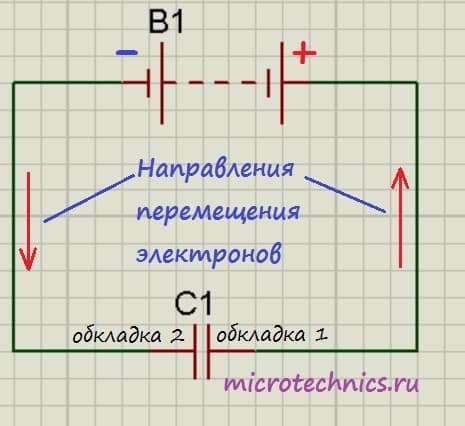
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что будет происходить?
Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной.
Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Именно так происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию. Как видите, здесь нет ничего сложного.
Емкость и энергия конденсатора.
Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда q одного из проводников к разности потенциалов между проводниками:
Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является неимоверно большой, поэтому чаще всего используются микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:
Здесь у нас d — это расстояние между пластинами конденсатора, а q — заряд конденсатора. Подставим эту формулу в выражение для емкости:
Если в качестве диэлектрика выступает воздух, то во всех формулах можно подставить varepsilon = 1 . Для запасенной же энергии конденсатора справедливы следующие выражения:
Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.
Итак, резюмируем — сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики, так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку.
Как найти площадь пластины конденсатора
Если двум изолированным друг от друга проводникам сообщить заряды 1 и 2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников. Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой . Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: 1 = – 2 = . В этом случае можно ввести понятие электрической емкости .
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда одного из проводников к разности потенциалов Δφ между ними:
В системе СИ единица электроемкости называется фарад (Ф):
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами , а проводники, составляющие конденсатор, – обкладками .
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским . Электрическое поле плоского конденсатора в основном локализовано между пластинами (рис. 1.6.1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния . В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками (рис. 1.6.2). Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля (см. § 1.4).
Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением (см. § 1.3)
Согласно принципу суперпозиции, напряженность поля, создаваемого обеими пластинами, равна сумме напряженностей и полей каждой из пластин:
Внутри конденсатора вектора и параллельны; поэтому модуль напряженности суммарного поля равен
Вне пластин вектора и направлены в разные стороны, и поэтому = 0. Поверхностная плотность σ заряда пластин равна , где – заряд, а – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна , где – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
(сферический конденсатор),
(цилиндрический конденсатор).
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов (рис. 1.6.3) напряжения на конденсаторах одинаковы: 1 = 2 = , а заряды равны 1 = 1 и 2 = 2. Такую систему можно рассматривать как единый конденсатор электроемкости , заряженный зарядом = 1 + 2 при напряжении между обкладками равном . Отсюда следует
Таким образом, при параллельном соединении электроемкости складываются.
При последовательном соединении (рис. 1.6.4) одинаковыми оказываются заряды обоих конденсаторов: 1 = 2 = , а напряжения на них равны и Такую систему можно рассматривать как единый конденсатор, заряженный зарядом при напряжении между обкладками = 1 + 2. Следовательно,
При последовательном соединении конденсаторов складываются обратные величины емкостей.
Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.
Площадь пластины (обкладки) в плоском конденсаторе. Калькулятор онлайн.
Онлайн калькулятор вычисления площади пластины (обкладки) в плоском конденсаторе, позволит найти площадь пластины (обкладки) через электроёмкость и расстояние между пластинами, а также через расстояние между пластинами, напряжение и заряд на пластине. Калькулятор произведет вычисление и даст подробное решение. Единицы измерения, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие.
Калькулятор содержит:
Площадь пластины (обкладки) в плоском конденсаторе через электроёмкость и расстояние между пластинами.
Площадь пластины (обкладки) в плоском конденсаторе через расстояние между пластинами, напряжение и заряд на пластине.
Площадь пластины (обкладки) в плоском конденсаторе через электроёмкость и расстояние между пластинами
Плоский конденсатор представляет собой две параллельные проводящие пластины, разделенные диэлектриком, расположенные на малом расстоянии друг от друга.
Площадь пластины (обкладки) в плоском конденсаторе через электроёмкость и расстояние между пластинами определяется формулой, где
ε0 – электрическая постоянная, ε0 = 8.85418781762039 × 10-12
ε – диэлектрическая проницаемость диэлектрика
C – емкость плоского конденсатора
d – расстояние между пластинами
Единица измерения площади является – Метр квадратный (м2, m2).
Диэлектрическая проницаемость ε =
Электроемкость C
Расстояние между пластинами d =
Единица измерения площади S
Площадь пластины (обкладки) в плоском конденсаторе через расстояние между пластинами, напряжение и заряд на пластине
Плоский конденсатор представляет собой две параллельные проводящие пластины, разделенные диэлектриком, расположенные на малом расстоянии друг от друга.
Площадь пластины (обкладки) в плоском конденсаторе через расстояние между пластинами, напряжение и заряд на пластине определяется формулой, где
ε0 – электрическая постоянная, ε0 = 8.85418781762039 × 10-12
ε – диэлектрическая проницаемость диэлектрика
Q – заряд на пластине
d – расстояние между пластинами
U – напряжение
Единица измерения площади является – Метр квадратный (м2, m2).
Диэлектрическая проницаемость ε =
Заряд Q =
Расстояние между пластинами d =
Напряжение U =
Единица измерения площади S
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Плоский конденсатор
Определение 1
Плоский конденсатор – это самый простой конденсатор, который представляет собой две плоские проводящие пластины, называемые обкладками, расположенные параллельно друг другу, разделенные диэлектриком, причем расстояние между пластинами должно быть намного меньше, чем размеры пластин.
Конденсаторы наравне с резисторами являются наиболее используемыми электронными компонентами. Самым интересным случаем является тот, когда заряды пластин плоского конденсатора противоположны по знаку и одинаковы по модулю, как представлено на рисунке ниже.
Рисунок 1. Конденсатор. Автор24 — интернет-биржа студенческих работ
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
На пластинах сосредоточен заряд – между ними возникает электрическое поле. У плоского конденсатора электрическое поле в основном сосредоточено между его обкладками, но в окружающем пространстве также имеет место быть электрическое поле, которое называется полем рассеяния. При решении задач им, в большинстве случаев, пренебрегают. Чтобы определить величины данного поля, необходимо рассмотреть схематическое изображение плоского конденсатора, которое представлено на рисунке ниже.
Рисунок 2. Плоский конденсатор. Автор24 — интернет-биржа студенческих работ
Каждой пластиной конденсатора создается электрическое поле:
- положительно заряженная частица +q создающая электрическое поле напряженностью Е+;
- отрицательно заряженная частица -q создающая электрическое поле напряженностью Е-.
«Плоский конденсатор: примеры решения задач» 👇
Формула для расчета напряженности поля для равномерно заряженной пластины выглядит следующим образом:
$Епл = j / (2*e¬_0*e)$
где: j – поверхностная плотность заряда; е – диэлектрическая проницаемость диэлектрического слоя между обкладками конденсатора.
Определение 2
Плотность заряда – это величина электрического заряда, который приходится на одну единицу объема, площади или длины, измеряющаяся в кулонах на метр.
Так как площадь пластин у рассматриваемого конденсатора одинакова, то модули напряженности равны между собой:
$Е+ = Е- = q / (2*e_0*e*S)$
где S – площадь пластин.
Однако направление векторов разные, то есть внутри конденсатора векторы направлены в одну сторону, а вне его в противоположные. Поэтому внутри пластин результирующее поле определяется следующим образом:
$Е = Е+ + Е- = (q / (2*e_0*e*S)) + (q / (2*e_0*e*S)) = q / (e_0*e*S)$
Таким образом вне плоского конденсатора электрические поля обкладок компенсируют друг друга – результирующая напряженность равна 0.
Примеры решения задач
Предположим, что необходимо рассчитать расстояние между пластинами плоского конденсатора при следующих условиях: разность потенциалов равняется 150 вольт, заряд на обкладке конденсатора равняется $10^{-8}$ кулон, площадь пластин 10^{-2}$ метра диэлектрический слой сделан из слюд, диэлектрическая проницаемость которой равняется 7. метра диэлектрический слой сделан из слюд, диэлектрическая проницаемость которой равняется 7.
Емкость конденсатора рассчитывается по следующей формуле:
$С = (е*е_0*S) / d$
где: е – диэлектрическая проницаемость слюды; е0 – диэлектрическая проницаемость вакуума; S – площадь пластин; d – расстояние между пластинами.
Определение 3
Диэлектрическая проницаемость – это коэффициент, который входит в математическую запись закона Кулона для силы взаимодействия между точечными зарядами, находящимися в однородной диэлектрической (изолирующей) среде на определенном расстоянии друг от друга.
Из представленной выше формулы можно вывести формулу для расчета расстояния между пластинами:
$d = (е*е_0*S) / С$
Емкость любого конденсатора может быть рассчитана по формуле:
$С = q/U$
где q – заряд на обкладке конденсатора; U – разность потенциалов.
Таким образом получается следующая формула для расчета расстояния между пластинами:
$d = (U*e*e_0*S) / q = (150*7*8.85*10^{-12}*10^{-2}) / 10^{-8} = 9.3 * 10^{-3}$
Предположим, что необходимо рассчитать первоначальную энергию плоского воздушного конденсатора и его энергию, если пластины раздвинуть до расстояния $1,5*10^{-2}$ при следующих исходных данных: первоначальная разность потенциалов 500 вольт, площадь пластин $2*10^{-2}$ метра, первоначальное расстояние между обкладками конденсатора $1,5-10^{-3}$, а источник напряжения в случае раздвижения пластин не отключается.
Энергия электрического поля конденсатора можно рассчитать по следующей формуле:
$W = (C*U^2) / 2$
где С – электрическая емкость конденсатора; U – разность потенциалов.
Электрическая емкость плоского конденсатора рассчитывается по формуле:
$С = (е*е_0*S) / d$
Если учесть, что рассматриваемый конденсатор воздушный, то первоначальная емкость может быть рассчитана – электрическая проницаемость воздуха равняется 1, по формуле:
$С_1 = (е_0*S) / d_1$
где, $d_1$ – первоначальная емкость конденсатора.
В таком случае первоначальная энергия конденсатора рассчитывается по формуле:
$W_1 = ((е_0*S) / d_1) * ((C*U^2) / 2) = (8.85 * 10 ^{-12}*2*10^{-2}*500^2) / (2*1.5*10^{-3}) = 14.8 * 10^{-6}$
При изменении расстоянии между обкладками конденсатора и не выключенном источнике напряжения разность потенциалов не меняется и, следовательно, формула для расчета энергии конденсатора при именном расстоянии между пластинами имеет следующий вид:
$W_2 = ((е_0*S)/d_2) * (U^2/2) = W_1*(d_1/d_2) = 14.8*10^{-6} * (1.5*10^{-3} / 1.5*10^{-2}) = 1.5 * 10^{-6}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме