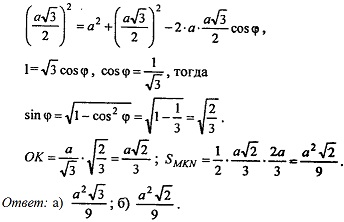Как найти площадь плоскость сечения тетраэдры - Сайт, где вы сможете решить свои вопросы

я могу помочь с этим заданием

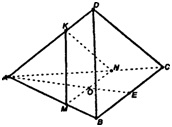
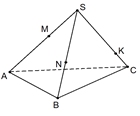
а) Пусть т. О – центр грани АВС. Построим МК || DB, MN || ВС.
пл .MKN – искомое сечение.
Пусть ребро тетраэдра равно а. Тогда

Т.к. ΔADB – равносторонний, а КМ || DB, то ΔАМК – также равносторонний, АМ=КМ=
(углы с соответственно параллельными и одинаково направленными сторонами):

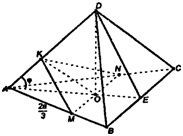
б) Построим отрезок в пл. ADO. Т.к. пл.то
Т.к. и то
Значит, ΔKMN — искомое сечение,
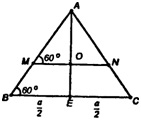
ΔAMN – равносторонний, MN = AM =

Из ΔADE по теореме косинусов имеем:
DE² = AD² + АЕ² – 2 ∙ AD ∙ АЕ ∙ cos φ,

Источник

Тетраэдр. Построение сечений тетраэдра

План урока

Тетраэдр;
Построение сечений тетраэдра.

Цели урока

Знать, что такое тетраэдр и как называются его элементы;
Знать, что понимают под сечением тетраэдра;
Уметь строить сечения тетраэдров.

Разминка

Какая фигура на плоскости называется многоугольником?
Что представляет собой множество всех общих точек двух различных непараллельных плоскостей?
Две параллельные плоскости пересечены третьей (секущей) плоскостью. Что можно сказать о взаимном расположении прямых по которым секущая плоскость пересекает данные параллельные плоскости?
Боковые стороны трапеции параллельны плоскости α. Параллельны ли плоскость α и плоскость трапеции?
Прямая a пересекает плоскость α. Лежит ли в плоскости α хоть одна прямая, параллельная прямой α?

Рис. 1. Тетраэдр

Рассмотрим произвольный треугольник ABC и точку S, не лежащую в плоскости этого треугольника (рис. 1). Соединим точку S отрезками с вершинами треугольника ABC. В результате получим треугольники SAB, SBC, SCA. Пространственная фигура, состоящая из треугольников ABC, SAB, SBC, SCA называется тетраэдром и обозначается SABC.

Тетраэдр является разновидностью многогранников, которым будет посвящена одна из глав курса стереометрии.

Определение 1

Тетраэдр
– это многогранник, состоящий из треугольника, точки не лежащий в плоскости этого треугольника и трёх отрезков соединяющих данную точку с вершинами данного треугольника.

Треугольники, из которых состоит тетраэдр, называются
гранями
тетраэдра.

Стороны этих треугольников называются
рёбрами
тетраэдра.

Вершины этих треугольников называются
вершинами
тетраэдра.

Определение 2

Тетраэдр, у которого все грани — равносторонние треугольники, называется
правильным
.

Таким образом, тетраэдр SABC (как и любой другой тетраэдр) имеет четыре грани (ABC, SAB, SBC, SCA), шесть рёбер (AB, BC, AC, SA, SB, SC) и четыре вершины (S, A, B, C). Два ребра тетраэдра, не имеющие общих вершин, называют противоположными. На рисунке 1 парами противоположных рёбер являются SA и BC, SB и AC, SC и AB. Одну из граней можно рассматривать как основание тетраэдра. В этом случае остальные грани называют боковыми.

Упражнение 1

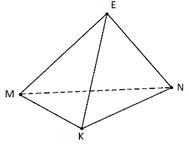
Изобразите треугольник MNK и точку E, не лежащую в плоскости этого треугольника. Соедините отрезками точку E с вершинами треугольника MNK.

а) Запишите обозначение тетраэдра, изображённого на полученном рисунке, а также все грани, рёбра и вершины этого тетраэдра.

б) Запишите пары противоположных рёбер этого тетраэдра.

Построение сечений тетраэдра

При решении многих стереометрических задач, связанных с тетраэдром, важно уметь строить на рисунке их сечения различными плоскостями. Разберём что называют сечением тетраэдра.

Определение 3

Секущая плоскость тетраэдра
– это плоскость по обе стороны от которой имеются точки данного тетраэдра.

Секущая плоскость тетраэдра пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки представляет собой сечение тетраэдра.

Определение 4

Сечение тетраэдра
—многоугольник, образованный пересечением плоскости с данным тетраэдром.

Тетраэдр имеет четыре грани, значит сечение тетраэдра не может иметь более четырёх сторон. Следовательно, сечением тетраэдра могут быть только треугольники и четырёхугольники.

Рассмотрим примеры построения различных сечений тетраэдра.

Рис. 2. К примеру 1

Пример 1

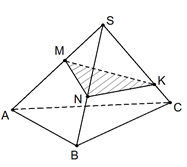
На рёбрах SA, SB, SC тетраэдра SABC отмечены точки соответственно M, N и K.

Построить сечение тетраэдра плоскостью MNK

Рис. 3. Решение

Решение

На рисунке 2 изображён исходный тетраэдр.

При построении сечений первым делом соединяем точки, лежащие на одних плоскостях (гранях). В данном случае точки M и N лежат в плоскости ABS, поэтому их соединяем. Аналогично N и K, M и K. Тогда плоскость MNK пересекает грани тетраэдра по отрезкам MN, NK и MK. В совокупности плоскость представляет собой треугольник MNK, который и является сечением данного тетраэдра.

Пример 2

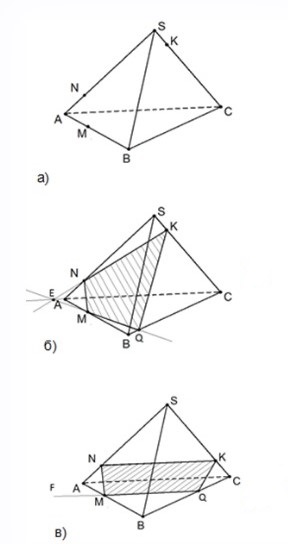
На рёбрах AB, SA, SC тетраэдра SABC отмечены точки соответственно M, N и K. Построить сечение тетраэдра плоскостью MNK.

Рис. 4. К примеру 2

Решение

Построим прямую, по которой плоскость MNK пересекает плоскость грани ABC. Точка M является общей точкой этих плоскостей. Чтобы построить ещё одну общую точку, продолжим отрезки KN и AC до их пересечения в точке E (рис. 4, б), которая и является второй общей точкой плоскостей MNK и ABC. Значит, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро BC в некоторой точке Q. Четырёхугольник MNKQ – искомое сечение.

Если точки N и K расположены таким образом, что прямые NK и AC параллельны, то прямая NK параллельна грани ABC и, следовательно, плоскость MNK пересекает грань ABC по некоторой прямой MF, параллельной NK. Вторая общая точка плоскостей ABC и MNK (точка Q) находится на пересечении MF и BC (рис. 4, в).

Пример 3

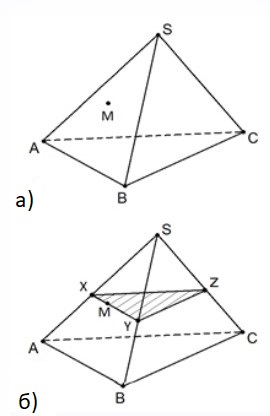
Точка M лежит на боковой грани ABS тетраэдра SABC (рис. 5, а).

Построить сечение тетраэдра плоскостью, проходящей через точку M параллельно основанию ABC.

Рис. 5. К примеру 3

Решение

Так как секущая плоскость параллельна плоскости ABC, то она параллельна прямым AB, BC и CA. Значит, секущая плоскость пересекает боковые грани тетраэдра по прямым, параллельным сторонам треугольника ABC. Проведём через точку M прямую, параллельную отрезку AB и обозначим буквами X и Y точки пересечения этой прямой с боковыми рёбрами SA и SB (рис. 5. б). Теперь через точку X проведём прямую, параллельную отрезку AC. Обозначим точку пересечения этой прямой с ребром SC буквой Z. Проведем отрезок YZ.

Треугольник XYZ является искомым сечением.

Упражнение 2

1. Может ли сечением тетраэдра быть:

а) треугольник;

б) четырёхугольник;

в) пятиугольник.

2. В тетраэдре SABC точки M, N, K – середины рёбер SA, SB, SC соответственно. Найдите площадь сечения тетраэдра SABC плоскостью MNK, если площадь треугольника ABC равна 80 см².

3. Изобразите тетраэдр SABC и отметьте точку M на ребре AB. Постройте сечение тетраэдра плоскостью, проходящей через точку M параллельно прямым AC и SB.

Контрольные вопросы

Какая геометрическая фигура называется тетраэдром?
Что представляет собой сечение тетраэдра?
Какие геометрические фигуры могут являться сечением тетраэдра?

Ответы

Упражнение 1

1.(рис. 6)

а) EMNK; грани – EMK, EKN, EMN, MNK; ребра – MK, KN, MN, EM, EK, EN; вершины – E, M, N, K.

б) MK и EN, MN и EK, KN и EM.

Рис. 6. К упражнению 1

Упражнение 2

1.а) да; б) да; в) нет

2. 20 см²

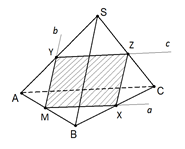
3. Через точку M проведём прямую a, параллельную AC;

обозначим точку пересечения прямых a и BC буквой X;

через точку M проведём прямую b, параллельную SB;

обозначим точку пересечения прямых b и SA буквой Y;

через точку Y проведём прямую c, параллельную AC;

обозначим точку пересечения прямых c и SC буквой Z;

Четырёхугольник MYZX – искомое сечение.

Рис. 7. К упражнению 2

Источник

: Категория: Математика; Опубликовано: 21 декабря 2021

В таблице даны самые необходимые формулы для фигуры тетраэдр — это нахождения площади, объема, высоты, сечения, ребра, поверхности.

Эту таблицу с формулами можно не только сохранить на компьютере, в закладках или вашей социальной сети. Но можно скачать и распечатать для использования на уроках.

Сохраните материал в вашей социальной сети, чтобы легко найти его:

Ответы на домашние задания:

Классификация по яркости раздел астрофизика
Что означает мораторий
Как найти количество протонов, нейтронов и электронов
Как делить в столбик, примеры деления на однозначное число
Где на карте мира расположена Албания
Русские слова в английском языке 4 класс
Теория всего. Искривленное пространство. Гравитационное поле. Физика.
Разделы астрономии: какой и что изучает.
Химический элемент Калий
Замораживания атомов газа
Что вызывает день и ночь?
Что такое юснатурализм
Разработана сверхтекучая жидкость с отрицательной массой
Потребности человека материальные, социальные, духовные – обществознание
Cлова на букву -А в английском языке

Источник

Геометрия. Объясните, пожалуйста, как найти площадь сечения тетраэдра.

мойше цехновицер

Ученик

(9),
на голосовании

7 лет назад

В тетраэдре DABC угол DBA = угол DBC = 90 градусов, DB = 6, AB = BC = 8, AC = 12. Постройте сечение тетраэдра плоскостью, проходящей через середину DB и параллельной плоскости ADC (построил). Найдите площадь сечения. Как это сделать?

Голосование за лучший ответ

Михаил Ужов

Эксперт пока не указал должность

7 лет назад

Две грани – прямоугольные треугольники. Стороны сечения – средние линии этих треугольников, равные половинам гипотенузы.
Гипотенуза равна √(DB²+AB²)=√(36+64)=10; Стороны равны по 5.
Третья сторона сечения равна половине АС, 12/2=6
А дальше – формула Герона:
р=(5+5+6)/2=8
S=√(8×3×3×2)=12

Юлия Коваленко

Мудрец

(18185)

7 лет назад

Можно и как сказал Михаил, но зачем такие сложности?

Допустим, обозначь точку сечения на стороне ВС как С1, на стороне АВ как А1, на стороне DВ как D1. У тебя получается, что СС1=С1В, АА1=А1В, DD1=D1B.Находишь D1B, С1В, А1В. По теореме Пифагора считаешь D1C1, А1D1. А1С1=1/2АС как средняя линия треугольника АВС. Итак, ты нашёл все стороны треугольника сечения и доказал, что он равнобедренный. Проводишь в нём высоту, считаешь её, по формуле S=1/2основания*высоту находишь его площадь.

Источник

Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через точки, делящие рёбра PC и BC в отношении 2:1, считая от вершины C, параллельно ребру BP, если все рёбра тетраэдра равны 3.

Спрятать решение

Решение.

Построим заданное сечение. Пусть точки K и L делят стороны BC и PC в отношении 2 : 1, так как сечение параллельно ребру PB, то и его следы будут параллельны этому ребру и будут делить ребра AP и AB в отношении 2 : 1, считая от вершины A. Таким, образом, прямоугольник KLMN  — искомое сечение.

Треугольники CKL и CPB подобны по двум углам, тогда имеем откуда KL  =  10. Аналогично получим, что ML  =  1. Таким образом, получим: