Как найти площадь по координатам вершин формула - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 января 2022 года; проверки требуют 2 правки.

Формула площади Гаусса (формула землемера или формула шнурования или алгоритм шнурования) — формула определения площади простого многоугольника, вершины которого заданы декартовыми координатами на плоскости. В формуле векторным произведением координат и сложением определяется площадь области, охватывающей многоугольник, а затем из нее вычитается площадь окружающего многоугольника, что дает площадь многоугольника внутри. Также она называется формулой шнурования, так как положительные и отрицательные слагаемые, состоящие из перемножаемых координат, располагаются крест-накрест, как при завязывании шнурков. Она находит применение в геодезии, лесном хозяйстве и других областях.

Формула была описана Мейстером (1724—1788) в 1769 году и Гауссом в 1795 году. Она может быть проверена путём деления многоугольника на треугольники, но её также можно рассматривать как частный случай теоремы Грина.

Формула определения площади определяется путём взятия каждого ребра многоугольника АВ и вычисления площади треугольника АВО с вершиной в начале координат О через координаты вершин. При обходе вокруг многоугольника образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника. Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется, если она слева, и вычитается, если она справа с точки зрения из начала координат.

Формула площади верна для любого самопересекающегося многоугольника, который может быть выпуклым или вогнутым.

Определение[править | править код]

Формула может быть представлена следующим выражением:

${displaystyle {begin{aligned}mathbf {S} &={frac {1}{2}}left|sum _{i=1}^{n-1}x_{i}y_{i+1}+x_{n}y_{1}-sum _{i=1}^{n-1}x_{i+1}y_{i}-x_{1}y_{n}right|=\&={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+dots +x_{n-1}y_{n}+x_{n}y_{1}-x_{2}y_{1}-x_{3}y_{2}-dots -x_{n}y_{n-1}-x_{1}y_{n}|,end{aligned}}}$

где

S — площадь многоугольника,

n — количество сторон многоугольника,

(x_i, y_i), i = 1, 2, …, n — координаты вершин многоугольника.

Другое представление этой же формулы^[1]^[2]:

${displaystyle {begin{aligned}mathbf {S} &={frac {1}{2}}left|sum _{i=1}^{n}x_{i}(y_{i+1}-y_{i-1})right|=\&={frac {1}{2}}left|sum _{i=1}^{n}y_{i}(x_{i+1}-x_{i-1})right|=\&={frac {1}{2}}left|sum _{i=1}^{n}x_{i}y_{i+1}-x_{i+1}y_{i}right|=\&={frac {1}{2}}left|sum _{i=1}^{n}det {begin{pmatrix}x_{i}&y_{i}\x_{i+1}&y_{i+1}end{pmatrix}}right|,end{aligned}}}$

где

x_n+1 = x₁, x₀ = x_n,

y_n+1 = y₁, y₀ = y_n.

Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны, и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, то детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина.

Примеры[править | править код]

Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости. Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую координату x первой вершины и умножим её на координату y второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определён по следующей формуле^[3]:

${displaystyle mathbf {S} _{text{tri.}}={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|,}$

где x_i и y_i обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3.

Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x₅ и y₅:

${displaystyle mathbf {S} _{text{pent.}}={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|.}$

S для четырехугольника — переменные до x₄ и y₄:

${displaystyle mathbf {S} _{text{quad.}}={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{1}y_{4}|.}$

Более сложный пример[править | править код]

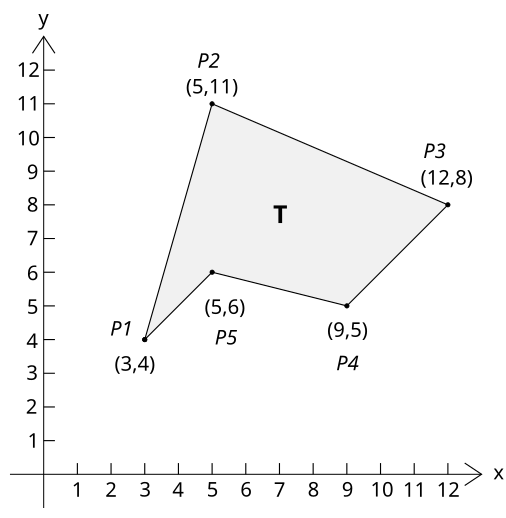
Рассмотрим многоугольник, представленный на рисунке и заданный точками (3, 4), (5, 11), (12, 8), (9, 5), (5, 6):

Площадь этого многоугольника:

${displaystyle {begin{aligned}mathbf {S} &={frac {1}{2}}|3times 11+5times 8+12times 5+9times 6+5times 4-{}\&qquad -4times 5-11times 12-8times 9-5times 5-6times 3|=\&={frac {60}{2}}=30.end{aligned}}}$

Объяснение названия[править | править код]

Формула называется «формулой шнурков» из-за общего метода, используемого для её вычисления. Этот метод использует матрицу. В качестве примера возьмём треугольник с вершинами (2, 4), (3, −8), (1, 2). Затем построим следующую матрицу, «обходя вокруг» треугольника и заканчивая начальной точкой:

${displaystyle {begin{bmatrix}2&4\3&-8\1&2\2&4end{bmatrix}}.}$

Сначала проведём диагональ вниз и вправо косой чертой, как показано ниже:

и перемножим пары чисел, соединённых чертой, а затем сложим все суммы:

(2 × −8) + (3 × 2) + (1 × 4) = −6.

Сделаем то же самое, проводя косую черту по диагонали вниз и влево, как показано ниже:

(4 × 3) + (−8 × 1) + (2 × 2) = 8.

Затем вычтем сумму второй группы из первой и возьмём модуль:

|(−6) − (8)| = 14.

Деление результата на два даёт площадь.
Организация чисел в матрицу с диагональными линиями упрощает запоминание формулы.
В результате проделанной операции с рисованием диагональных (косых) линий матрица с числами напоминает зашнурованную обувь, отсюда и происходит название «алгоритма шнурования».

Хорошее описание “Шнуровки Гаусса” представлено в видео на канале Wild Mathing [1]

См. также[править | править код]

Планиметр
Теорема Грина

Примечания[править | править код]

↑ Shoelace Theorem Архивная копия от 23 сентября 2020 на Wayback Machine, Art of Problem Solving Wiki.
↑ Weisstein, Eric W. Polygon Area. Wolfram MathWorld. Дата обращения: 24 июля 2012. Архивировано 12 мая 2012 года.
↑ Richard Rhoad; George Milauskas; Robert Whipple. Geometry for Enjoyment and Challenge. — new. — McDougal Littell (англ.) (рус., 1991. — С. 717—718. — ISBN 0-86609-965-4.

Источник

Площадь по заданным координатам.

Как найти (вычислить) площадь фигуры (треугольник, четырехугольник, трапеция, многоугольник и др.) по координатам?

Какие есть формулы и методы, позволяющие находить площадь через координаты?

бонус за лучший ответ (выдан): 5 кредитов

Для вычисления площади простого многоугольника с любым количеством вершин, представленных в виде списка координат, при последовательном обходе которых, не образуются пересекающиеся линии, применяется формула Гаусса, иначе называемая “формулой землемера”, “формулой геодезиста”, “формулой шнурования”, “алгоритмом шнурования”, а так же “методом треугольников”.

Суть метода заключается в построении треугольников, состоящих из сторон многоугольника и лучей проведённых из начала координат к вершинам многоугольника, и сложении площадей треугольников, включающих внутреннюю часть многоугольника с вычитанием площадей треугольников, расположенных снаружи.

Площадь, вычисленная по приведенной формуле, будет иметь отрицательное значение при обходе фигуры по часовой стрелке и положительное при обходе против часовой стрелки.

Фигура многоугольника может иметь произвольную геометрию. Например:

Список координат многоугольника представлен в виде массива: (x1, y1), (x2, y2), (x3, y3),…(xn, yn).

Для многоугольника на первом рисунке он задан точками: (3,4), (5,11), (12,8), (9,5), (5,6). Его площадь будет равна:

Существует также метод трапеций, основанный на сложении и вычитании площадей трапеций, образованных каждой из сторон многоугольника, её проекцией на ось абсциссы и перпендикулярами, опущенных из вершин на абсциссу. При обходе вершин по часовой стрелке учитывается величина координаты вершин. Если первая вершина меньше второй, то площадь трапеции прибавляется, если нет, то отнимается.

Для многоугольника ABCDE на левом нижнем рисунке существует 5 трапеций : ABJH, CBJF, CDIF, EDIG и EAHG.

Так как X1<X2, X3<X4 и X5<X1, то площади трапеций ABJH, CDIF и EAHG складываются, а X3>X4 и X4<X5, следовательно, площади трапеций CBJF и EDIG вычитаются:

S = S(ABJH) – S(CBJF) + S(CDIF) – S(EDIG) + S(EAHG)

Площади трапеций рассчитываются по формуле;

Sтрапеции = 1/2 *((a+b))*h,

где a, b – основания трапеции,

h – высота трапеции.

Значения a, b и h вычисляются по координатам.

В декартовых координатах круг может быть представлен двумя точками: центр А и любая точка В, лежащая на окружности. Для расчета площади круга необходимо вычислить его радиус по формуле:

автор вопроса выбрал этот ответ лучшим

Ксарфакс
[156K]

5 лет назад

Площадь фигуры по координатам вершин

Если известны координаты всех вершин, то площадь заданной геометрической фигуры (треугольника, прямоугольника, трапеции, ромба и т.д) можно найти по стандартным формулам. Но предварительно нужно найти длину сторон, диагоналей и т.п. (всё зависит от фигуры) с помощью формулы нахождения длины отрезка по заданным координатам.

Эта формула выглядит следующим образом:

Здесь:

AB – отрезок,

точка A имеет координаты (x1, y1),

точка B имеет координаты (x2, y2).

Рассмотрим несколько примеров.

1) Треугольник ABC имеет координаты A(2,3); B(6,7); C(5,0). Его площадь можно найти по формуле Герона:

Здесь:

S – площадь треугольника,

a, b, c – стороны,

p – полупериметр, который равен половине суммы сторон a, b и c.

Найдём, чему равны стороны треугольника по формуле нахождения длины отрезка по координатам:

AB = √(4² + 4²) = √32 ≈ 5,66.

AC = √(3² + (-3)²) = √18 ≈ 4,24.

BC = √((-1)² + (-7)²) = √50 ≈ 7,07.

Полупериметр треугольника будет равен (5,66 + 4,24 + 7,07) / 2 ≈ 16,97 / 2 ≈ 8,49.

Отсюда площадь треугольника ABC ≈ √(8,49 * 2,83 * 4,25 * 1,42) ≈ √145 ≈ 12,04.

2) Ромб ABCD имеет координаты A(1,2); B(3,4); C(5,2); D(3,0). Площадь можно найти через диагонали:

Здесь:

S – площадь ромба,

d1 и d2 – диагонали.

Таким образом, нам нужно найти диагонали AC и BD.

AC = √(4² + 0) = √16 = 4.

BD = √(0 + (-4)²) = √16 = 4.

Отсюда площадь ромба ABCD = 0,5 * 4 * 4 = 8.

3) Трапеция ABCD имеет координаты A(1,1); B(3,4); C(5,4); D(6,1). Стандартная формула площади трапеции такая:

Здесь:

S – площадь трапеции,

a и b – основания,

h – высота.

Высота трапеции (пусть это будет BE) – это перпендикуляр, который был опущен из вершины трапеции (из точки B) на её основание (в нашем случае это AD).

Определим координаты её отрезка:

координаты первой точки совпадают с точкой B, это (3,4).
координаты 2 точки (точка E) будут (3,1) – так как абсцисса совпадает с абсциссой точки B, а ордината совпадает с ординатой точек A и D.

Высота трапеции BE = √(0 + (-3)²) = √9 = 3.

Теперь посчитаем длину оснований:

BC = √(2² + 0) = √4 = 2.

AD = √(5² + 0) = √25 = 5.

Таким образом, площадь трапеции ABCD = 3 * 0,5 * (2 + 5) = 10,5.

Степан-16
[34.5K]

5 лет назад

Первоначально нужно вычислить длины сторон. В этом здесь будет основная задача. Получив стороны, вычисляем площади по стандартным формулам.

Самый простой случай – для прямоугольника, когда его стороны параллельны осям координат. Тогда одна сторона будет равна разнице абсцисс, вторая ординат.

Треугольник. Допустим, основание параллельно оси абсцисс. Вычисляем его длину, как разницу абсцисс. Далее нужно найти высоту. Она будет равна разнице ординат третьей вершины и ординаты любой из вершин основания. Затем – площадь по формуле: половина произведения основания на высоту.

И т.д.

Если же стороны фигуры не параллельны осям, то находить длины сторон придется уже более сложными расчетами. Допустим, прямоугольник. Первую сторону будем искать, как если бы она была гипотенузой в составе прямоугольного треугольника. Каждая сторона будет равна квадратному корню из суммы квадратов абсцисс и ординат концов отрезков стороны.

Так и для любой фигуры. Вначале определяем длины сторон как гипотенузу треугольника. После чего применяем стандартные формулы площадей.

Эления
[445K]

3 года назад

Рассчитать площадь какой угодно геометрической фигуры, зная координаты, не составляет сложности. Каждая из точек, соответствующая вершинам искомой фигуры, будь это треугольник, четырех- или многоугольник, имеет определенную координату, а значит у нее есть значение, через которое можно рассчитать площадь.

Координаты, как найти на графике, чтобы узнать площадь фигуры? Проецируем на оси абсцисс и ординат прямые, проведя перпендикуляр из каждой точки. Полученные значения будут исходной величиной. Каждая из сторон фигуры – это разница двух точек на горизонтальную и вертикальную оси. Разница между значениями означает длину стороны фигуры. А зная все стороны и их значение, по формуле находим площадь.

Пример 1. Ищем площадь треугольника.

Мы видим два отрезка зеленого цвета AB и BC, которые образуют стороны равнобедренного треугольника, а основание есть отрезок на оси абсцисс AC.

Даны значения: AC основание в промежутке от “-4” до “+4”, то есть длина основания равна восьми.

Будет лучше, если посчитать площадь этого треугольника, как сумму из образовавших его двух треугольников, которые являются прямыми, ABO и BOC, совпадающие прямым углом с координатой “0” на графике.

Известна длина каждй из сторон, образующих прямой угол (AO или OC) х = 4 – 0 = 4 и y = 2 – 0 = 2 (BO).

Зная длину двух сторон, образующих прямой угол (AO и BO), находим длину основания (AB или BC). Тогда уже знаем все длины каждой из сторон обоих прямых треугольников. Остается только найти площадь по формуле:

Зная площадь каждого из прямых треугольников, умножаем на два, получаем сумму заштрихованного треугольника на графике ABC.

И еще математически можно записать решение следующим образом, исходя из того, что имеем изначально следующую систему неравенств:

Пример 2.

Пример 3. Есть парабола, ищем площадь фигуры, ограниченную кривой параболы. Чтобы посчитать, используем интеграл.

Бекки Шарп
[71.2K]

3 года назад

Рассмотрим простой случай, где буквально на пальцах можно посчитать площадь через обычную формулу, а затем применим к этой задаче формулу Гаусса.

У нас есть трапеция, у которой известны координаты вершин. (3:2) (5:2) (9:6) (6:6). Мы знаем, что площадь трапеции равна сумме оснований, деленной на 2 и умноженной на высоту.

S = (a+b)/2 х h Считаем площадь: S = (3+2):2х4 = 10. Ответ – 10.

А теперь по теореме Гаусса.

Не смотря на страшный вид, формула очень простая. В квадратных скобках мы перемножаем абсциссу первой точки с ординатой второй, прибавляем абсциссу второй, умноженную на ординату третьей и так идем по кругу фигуры. Далее вычитаем ординату первой умноженную на абсциссу второй и т.д. В квадратных скобках у нас может получиться отрицательное число.

S= 0,5 х [3х6+6х6+9х2+5х2 – 2х6-6х9-6х5-2х3] = 10

Таким образом можно найти площадь любой сложной фигуры, зная ее координаты.

dydySacha
[10.8K]

5 лет назад

Можно взять милиметровку и нанести точки с заданными координатами, согласно осей абсцис и ординат. Соединить эти точки между собой и замерить длины образовавшихся сторон, а с помощью формулы по определению площади образовавшейся фигуры узнать её значение подставив данные в эту формулу.

Алиса в Стране
[363K]

3 года назад

Существует специальная формула, называемая формулой Гаусса, она и позволит нам определить искомую площадь по координатам. Вот как эта формула выглядит:

Формула выглядит немного устрашающе, но давайте попробуем в ней разобраться. У нас есть многоугольник и есть его координаты, подсчитать n – количество сторон многоугольника несложно, а дальше просто нужно подставлять значения в эту формулу, нужно только быть внимательным и не перепутать какие координаты куда надо писать.

Давайте теперь приведем пример нахождения такой площади через формулу Гаусса. Допустим, у нас есть вот такой пятиугольник:

Координаты его пяти вершин, как мы видим: (3, 4), (5, 11), (12, 8), (9, 5), (5, 6).

Теперь нам остается только очень внимательно подставить эти координаты в нашу формулу, n = 5, координаты известны, вот что у нас получится:

Когда разбираешься в этой формуле, понимаешь, насколько она проста и даже легко запоминается, несмотря на то, что сначала кажется очень сложной.

duselldorf
[4.3K]

5 лет назад

Для вычисления площади геометрической фигуры по координатам ее вершин, нужно воспользоваться формулой Гаусса, иногда ее называют формулой землемера или формулой геодезиста, так как она применяется геодезистами для определения площади земельного участка, например, при межевании:

где

А – площадь многоугольника с заданными координатам его вершин,

n – количество сторон многоугольника,

(xi, yi) – координаты вершин многоугольника,

i = 1, 2,…, n — номер вершины многоугольника.

Бархатные лапки
[382K]

3 года назад

Находим площадь вот такого несложного четырехугольника. Координаты его вершин нам известны. Применяем формулу Гаусса, которая выглядит так:

S (площадь) = 0,5 [6х4 +9х7 + 10х6 + 7х3 – 3х9 – 4х10 – 7х7 – 6х6] = 8 (квадратных единиц)

Как видим если применять при решении формулу Гаусса то решить такую задачку несложно.

Не вижу здесь серьезных проблем. Мы, как я понял, имеем готовые точки координат, которые нужно проставить на координатной плоскости. Далее, соединяя эти точки, получаем фигуру, как в примере вопроса – квадрат, треугольник и т.п.

Теперь вычисляем площадь любой из полученных фигур по формуле ей соответствующей.

Знаете ответ?

Источник

Как найти площадь треугольника по координатам его вершин?

1способ:

Найти длины трёх сторон треугольника и вычислить площадь по формуле Герона. Способ удобен, если длины сторон являются целыми числами. В противном случае предстоят громоздкие вычисления.

2 способ:

вывести формулу для нахождения площади и использовать её для вычисления.

Утверждение

Площадь треугольника ABC с вершинами в точках A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) можно вычислить с помощью формулы

$[S_{Delta ABC} = frac{1}{2}left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} right|.]$

Доказательство:

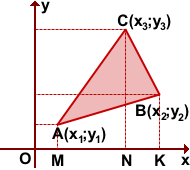Рассмотрим треугольник ABC,

A(x₁;y₁), B(x₂;y₂), C(x₃;y₃)

Опустим перпендикуляры из вершин треугольника на координатные оси.

$[S_{Delta ABC} = S_{MACN} + S_{NCBK} - S_{MABK} ]$

$[S_{MACN} = frac{{MA + CN}}{2} cdot MN = frac{{y_1 + y_3 }}{2} cdot (x_3 - x_1 ),]$

$[S_{NCBK} = frac{{NC + BK}}{2} cdot NK = frac{{y_3 + y_2 }}{2} cdot (x_2 - x_3 ),]$

$[S_{MABK} = frac{{MA + BK}}{2} cdot MK = frac{{y_1 + y_2 }}{2} cdot (x_2 - x_1 ).]$

$[S_{Delta ABC} = ]$

$[= frac{{y_1 + y_3 }}{2} cdot (x_3 - x_1 ) + frac{{y_3 + y_2 }}{2} cdot (x_2 - x_3 ) - frac{{y_1 + y_2 }}{2} cdot (x_2 - x_1 ) = ]$

$[= frac{1}{2}[(y_1 + y_3 )(x_3 - x_1 ) + (y_3 + y_2 )(x_2 - x_3 ) - (y_1 + y_2 )(x_2 - x_1 )] = ]$

$[= frac{1}{2}[x_3 y_1 - x_1 y_1 underline { + x_3 y_3 } - x_1 y_3 + x_2 y_3 underline { - x_3 y_3 } + x_2 y_2 - x_3 y_2 - ]$

$[= frac{1}{2}[(x_2 y_3 - x_2 y_1 ) + ( - x_1 y_3 + x_1 y_1 ) + (x_1 y_2 - x_1 y_1 ) + ]$

$[= frac{1}{2}[x_2 (y_3 - y_1 ) - x_1 (y_3 - y_1 ) + x_1 (y_2 - y_1 ) - x_3 (y_2 - y_1 )] = ]$

$[= frac{1}{2}[(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )].]$

С учетом вариантов взаимного расположения точек A, B и C формула для вычисления площади треугольника по координатам его вершин приобретает вид:

$[ S_{Delta ABC} = frac{1}{2}left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} right|. ]$

Что и требовалось доказать.

3 способ:

Найти длины двух сторон и косинус угла между ними и вычислить площадь треугольника через стороны и синус угла между ними.

4 способ:

Найти длину и уравнение одной стороны треугольника и длину высоты, проведённой к этой стороне. Вычислить площадь через сторону и высоту.

Рассмотрим эти способы на конкретном примере.

Найти площадь треугольника, вершины которого имеют координаты A(-1;-3), B(3;4), C(5;-5).

1 способ:

Находим длины сторон треугольника ABC.

$[AB = sqrt {(x_B - x_A )^2 + (y_B - y_A )^2 } ]$

$[ AB = sqrt {(3 - ( - 1))^2 + (4 - ( - 3))^2 } = sqrt {16 + 49} = sqrt {65} ;]$

$[AC = sqrt {(x_C - x_A )^2 + (y_C - y_A )^2 } ]$

$[AC = sqrt {(5 - ( - 1))^2 + ( - 5 - ( - 3))^2 } = sqrt {36 + 4} = sqrt {40} ;]$

$[BC = sqrt {(x_C - x_B )^2 + (y_C - y_B )^2 } ]$

$[BC = sqrt {(5 - 3)^2 + ( - 5 - 4)^2 } = sqrt {4 + 81} = sqrt {85} .]$

Поскольку длины сторон выражены иррациональными числами, вычислять площадь треугольника по формуле Герона — не самый лучший способ.

2 способ:

Подставляем в формулу x₁=-1, y₁=-3, x₂=3, y₂=4, x₃=5, y₃=-5:

$[S_{Delta ABC} = frac{1}{2}left| {(3 - ( - 1))( - 5 - ( - 3)) - (5 - ( - 1))(4 - ( - 3))} right| = ]$

$[= frac{1}{2}left| {4 cdot ( - 2) - 6 cdot 7} right| = frac{1}{2} cdot 50 = 25.]$

3 способ:

Угол A образован векторами AC и AB. Отсюда

$[ cos angle A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{{left| {overrightarrow {AB} } right| cdot left| {overrightarrow {AC} } right|}} ]$

Находим координаты векторов:

$[overrightarrow {AB} (x_B - x_A ;y_B - y_A )]$

$[overrightarrow {AC} (x_C - x_A ;y_C - y_A )]$

Скалярное произведение

Длины AB и AC уже знаем:

$[cos angle A = frac{{10}}{{sqrt {65} cdot sqrt {40} }} = frac{{10}}{{sqrt {5 cdot 13} cdot sqrt {5 cdot 4 cdot 2} }} = ]$

$[= frac{{10}}{{5 cdot 2sqrt {26} }} = frac{1}{{sqrt {26} }}.]$

Синус и косинус одного угла связаны соотношением:

Синус угла от 0° до 180° является положительным числом, поэтому

$[sin angle A = sqrt {1 - cos ^2 angle A} ]$

$[sin angle A = sqrt {1 - frac{1}{{26}}} = sqrt {frac{{25}}{{26}}} = frac{5}{{sqrt {26} }}.]$

Отсюда

$[S_{Delta ABC} = frac{1}{2} cdot AB cdot AC cdot sin angle A,]$

$[S_{Delta ABC} = frac{1}{2} cdot sqrt {65} cdot sqrt {40} cdot frac{5}{{sqrt {26} }} = 25.]$

4 способ:

Найдём уравнение прямой AB. Подставляем координаты A и B в уравнение y=kx+b:

$[left{ begin{array}{l} - 3 = k cdot ( - 1) + b \ 4 = k cdot 3 + b \ end{array} right.]$

Отсюда k=7/4, b=-5/4

$[y = frac{7}{4}x - frac{5}{4},4y = 7x - 5,]$

Найдём расстояние от точки C до прямой AB:

$[d = frac{{left| {7 cdot 5 - 4 cdot ( - 5) - 5} right|}}{{sqrt {7^2 + 4^4 } }} = frac{{50}}{{sqrt {65} }}.]$

Это расстояние равно высоте треугольника, проведённой из вершины C к стороне AB. Отсюда

$[S_{Delta ABC} = frac{1}{2} cdot AB cdot d = frac{1}{2} cdot sqrt {65} cdot frac{{50}}{{sqrt {65} }} = 25.]$

Источник

Невероятный алгоритм, который я, за свои 30 лет нигде и никогда раньше не встречал. Решил поделиться с Вами, надеюсь, будет интересно!

Давненько не было математики… один космос, да космос. А ведь раньше на канале было полным полно математики, а теперь что?.. Но, этому есть объяснение. Полгода назад стал папкой сразу двух сыновей, и сами понимаете, времени для творчества совсем мало, прям критически мало.

Так вот, что там с формулой Гаусса?

Давайте представим, что у нас есть треугольник с координатами вершин (1,1), (5,2), (2,5) и стоит задача найти его площадь.

Невероятно редкая формула площади. "Шнуровка Гаусса"

Выписываем координаты вершин в 2 столбца, начиная двигаться по контуру треугольника против часовой стрелки. В левый столбец – координата “х”, в правый – координата “у”. Последняя координата в конце повторяется.

Далее, перемножаем столбцы между собой. Для начала, берем “Зеленое” направление, а затем “красное”.

Этот алгоритм называют “Шнуровкой Гаусса”, просто посмотрите на внешний вид…

Итак, перемножаем координаты и складываем. Должно в итоге получится 2 числа:

Площадь фигуры находится как половина разности 29-ти и 14-ти.

Проверить данное число крайне просто, учитывая, что все построения я выполнял в CAD системе (1 ед = 10мм).

По этому же принципу можно вычислить площадь любого многогранника. Достаточно просто знать координаты.

Вот вам примерчик “на дом” для тренировки. Попробуйте вычислить площадь, и делитесь ответами в комментариях!

Подписывайтесь и ставьте лайки, если было интересно!

Источник

Площадь треугольника по координатам вершин – формулы для расчета

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

делящий противоположную углу сторону пополам — медиана;
разделяющий угол при вершине на два равных — биссектриса;
падающий под прямым углом на противоположную углу сторону — высота.

Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

Тогда координаты его векторов AB- и AC- выразятся так:

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

Необходимо определить координаты векторов, образующих стороны треугольника.
Затем, следует вычислить длины их сторон.
Посчитать полупериметр фигуры.
Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1 2 + y1 2 )^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

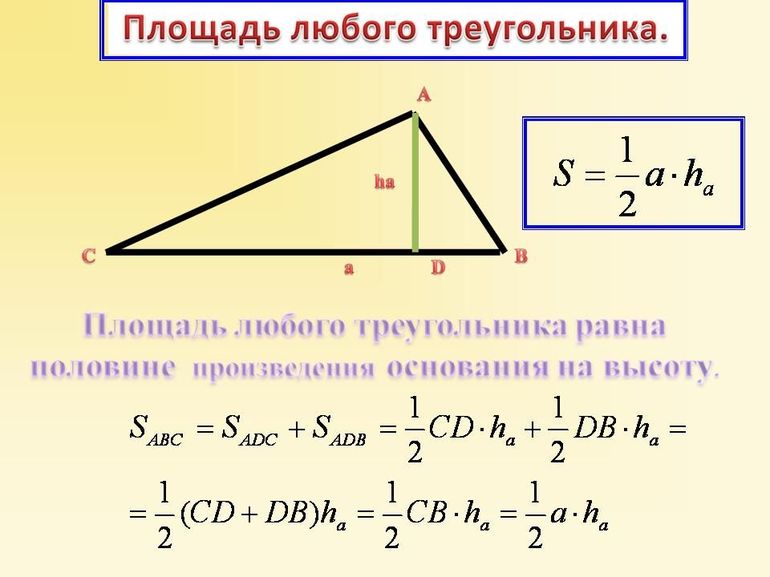
Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

Онлайн калькулятор. Площадь треугольника построенного на векторах.

Этот онлайн калькулятор позволит вам очень просто найти площадь треугольника построенного на векторах.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади треугольника построенного на векторах и закрепить пройденый материал.

Калькулятор для вычисления площади треугольника построенного на векторах

Выберите каким образом задается треугольник:

Введите значения векторов: Введите координаты точек:

Инструкция использования калькулятора для вычисления площади треугольника построенного на векторах

Ввод данных в калькулятор для вычисления площади треугольника построенного на векторах

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления площади треугольника построенного на векторах

Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.

Теория. Площадь треугольника построенного на векторах

Определение Площадь треугольника образованного векторами a и b равна половине модуля векторного произведения этих векторов:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Вычисление площади треугольника построенного на векторах.

Этот калькулятор онлайн вычисляет площадь треугольника построенного на векторах. Треугольник может быть задан координатами двух векторов или координатами трех вершин треугольника.

Онлайн калькулятор для вычисления площади треугольника построенного на векторах не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac<2> <3>)

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac<5> <7>)

[spoiler title=”источники:”]

http://ru.onlinemschool.com/math/assistance/vector/triangle_area/

http://www.math-solution.ru/math-task/vect-area-triangle

[/spoiler]

Источник

Определение[править | править код]

Примеры[править | править код]

Более сложный пример[править | править код]

Объяснение названия[править | править код]

См. также[править | править код]

Примечания[править | править код]

Площадь фигуры по координатам вершин

Площадь треугольника по координатам вершин – формулы для расчета

Самый простой многоугольник и вектор

Фигура на плоскости

Направленный отрезок

Методы вычисления площади по координатам

Универсальный подход

Использование формулы Герона

Другие способы

Решение задачи

Онлайн калькулятор. Площадь треугольника построенного на векторах.

Калькулятор для вычисления площади треугольника построенного на векторах

Инструкция использования калькулятора для вычисления площади треугольника построенного на векторах

Ввод данных в калькулятор для вычисления площади треугольника построенного на векторах

Дополнительные возможности калькулятора вычисления площади треугольника построенного на векторах

Теория. Площадь треугольника построенного на векторах

Решение задач по математике онлайн

Калькулятор онлайн.Вычисление площади треугольника построенного на векторах.

Вам также может понравиться

Как найти число символов в тексте

Поднялась плитка на полу как исправить

Как найти свое айпи видео

Добавить комментарий Отменить ответ

Калькулятор онлайн.
Вычисление площади треугольника построенного на векторах.