а – длина листа вдоль главной жилки, измеряемая от места соединения черешка с листовой пластиной растения, или же от заднего выступа листа для утопающего в листовой пластине черешка (лист №4 в таблице 2), до конца вершинки листа, см;
b – ширина листа по крайним точкам поперек листовой пластины, или же общая ширина листа в наибольших двух поперечных сечениях листа растения, поэтому при замерах половинок она определяется как сумма максимальной ширины у каждой половинки измеряемого листа, см;
b/a – отношение ширины к длине листа;
Sab- площадь прямоугольника длиной а и шириной b, описанного вокруг измеряемого листа, см2;
Sф- фактическая (измеренная по сантиметровым и малым клеткам сетки палетки) на фотоизображении площадь листа, см2;
Кn- коэффициент площади, показывающий отношение фактической площади листа к площади описанного прямоугольника.
В таблице 1 приведены вспомогательные для проведения измерений геометрические параметры:
Sпр- площадь прямоугольника, выделенного на фотоснимке листа с палеткой по целым сантиметровым клеткам (фиг.2), см2;
nц- целые сантиметровые клетки вокруг листовой пластины внутри прямоугольника, выделенного на фотоснимке, шт.;
nн- количество малых клеток в сетке палетки на нижней половинке листовой пластины, шт.;
nв- количество малых клеток в сетке палетки на верхней половинке листовой пластины, шт.
Для удобства измерений увеличенное изображение листа растения (фиг.2) распечатывается на принтере, а затем прямоугольник Sпрвыделяется на сетке, например, обводом шариковой ручкой или карандашом. Этот прием позволяет не терять внимательности при подсчете количества малых клеток на верхней и нижней половинках измеряемого листа.
На серийно изготовляемой палетке для картографических измерений приняты малые клетки размерами 2×2 мм. Можно изготовить самому такую палетку на прозрачном листе из пластмассы, например, из листов обложек папок для бумаг. При этом на прозрачном листе пластика, вырезанном больше размеров наиболее крупных листьев изучаемых древесных и иных растений, составляется сетка с миллиметровыми или двухмиллиметровыми клетками любыми доступными средствами, например, нанесением линий сетки тушью чертежным рейсфедером.
Формула для вычисления фактической площади листа изучаемого растения (в нашем примере малые клетки имеют стороны по 2 мм, поэтому на сантиметровой клетке находится 25 малых клеток):
Sф=Sпр-nц-(nн+nв)/25.
![]()
Например таких, чтобы было понятно о чём идет речь.

Нужно найти качественную бумагу (постоянной толщины), скопировать картинку в файл, распечатать его на той бумаге, вырезать каждую фигурку и взвесить. На бумаге нарисовать прямоугольник или квадрат известной площади, его тоже вырезать и взвесить. Площадь остальных фигурок найдутся из пропорции S(x)=S(квадрата)*(m(x)/m(квадрата)).
Если большая точность не нужна, то можно распечатать фигурки на прозрачной бумаге (кальке), наложить рисунки на миллиметровку и подсчитать количество клеток.
автор вопроса выбрал этот ответ лучшим
![]()
Татьяна Ьеглова
[169K]
7 лет назад
Накладываем на изображение фигуры прозрачный трафарет, например, из кальки, с нанесённой на него сеткой, состоящей из квадратных клеток, размер которых соответствует единице измерения площади фигуры. То есть, если площадь фигуры кратна квадратным сантиметрам, то сетка будет с ячейкой 1 см х 1 см.
Затем считаем количество целых клеток в пределах наружного контура фигуры. Записываем. Считаем количестве неполных клеток, делим его на два и прибавляем результат к числу целых клеток.
Всё это можно проделать также в программах Autocad или Archicad.
![]()
Nelli4ka
[114K]
7 лет назад
В геодезии, например, в этом случае прибегают к помощи квадратной палетки, которая представляет собой расчерченную в мелкую сетку прозрачную поверхность, например, из стекла.

Берем нашу фигуру произвольной формы и накладываем на нее палетку. Считаем, сколько квадратов у нас занято фигурой, а сколько – находятся в свободном от нее пространстве. Далее уже легко определяют площадь фигуры, прежде – вычисляют площадь квадрата палетки и отнимают от нее процентное соотношение свободных квадратов.
Фигуру нужно внести в квадрат, на этот квадрат нанести случайные точки, посчитать процентное соотношение точек попавших внутрь фигуры и снаружи. Высчитать площадь квадрата, из площади квадрата вычесть проценты точек оказавшихся снаружи фигуры.

![]()
Грустный Роджер
[397K]
7 лет назад
Проще всего планиметром. Это специальный измерительный инструмент для измерения площадей плоских фигур произвольной формы.
Если же планиметра нет, то придётся по клеточкам, как посоветовали в предыдущем ответе.
Знаете ответ?
Are you confused about measuring the area using square paper? Here you can find more information on measuring the area using square paper. This topic includes the definition of the area, How to measure the area using square paper. You can also check the examples for a better understanding of the concept.
Do Refer:
- Measuring Area in Square Units
- Find the Area of the Shaded Region
- Areas of Irregular Figures
Area – Definition
The area is defined as the amount of space occupied by the surface of an object. The area is measured in square units.
How to Measure the Area using Square Paper?
Here we will discuss how to measure the area using square paper. Take a square paper and draw any shape. We can determine the area covered by that shape by counting the no of squares. Steps to be followed for measuring the area are as follows
Step 1: Count the no of Full Squares
Step 2: Count the no of Half Squares also we know that two triangles make one square.
Step 3: If the square is more than half, consider it as 1.
Step 4: If the square is less than half, Don’t consider it. Thus we get the area of the figure.
Finding the Area using Square Paper Examples
Example 1:
Find the area of the below figure?
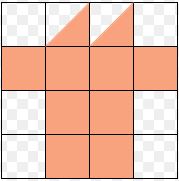
Solution:
No of squares=8
No of half squares=2
We know two half squares becomes one.
Total no of squares=8+1=9.
Therefore, the Area of the figure=9squnits.
Example 2:
Find the area of the below figure?
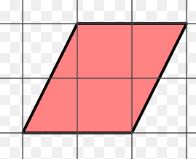
Solution:
since the first square is less than half don’t consider it.
The second one is full square.
The third one is more than half. So we have to consider it as one.
the fourth one is more than half. So we have to consider it as one.
The Fifth one is full square.
The sixth one is less than half. So don’t consider it.
No of Full squares=2
No of half squares=2 i.e. 1 square.
No of squares less than half is 2. So, we exclude the two squares.
Therefore, the total area of the figure is 2+1=3 sq units.
Example 3:
Find the area of the below figure?
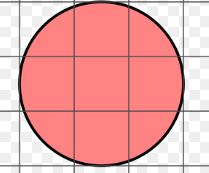
Solution:
No of Full squares=5
No of Half squares=4 i.e. 2 squares
Therefore, the total area of the figure is 5+2= 7 sq units.
Example 4:
Find the area of the below figure?
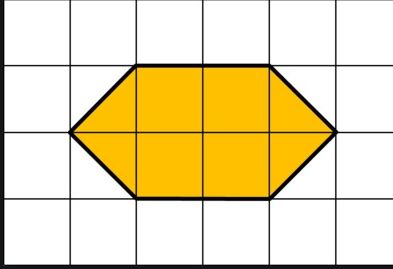
Solution:
Here no of Full squares=4
No of half squares=4 i.e. 2 squares
Therefore, the total area of the figure=4+2=6 sq units.
Example 5:
Measure the area of the below figure?
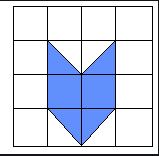
Solution:
No of Full squares=2
No of half squares=4 i.e. 2 squares
Therefore, the total area of the figure is 2+2=4 sq units.
Example 6.
Measure the area of the following figure?
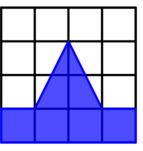
Solution:
No of Full squares=4
No of squares more than half=2
No of squares less than half=2. So don’t consider it.
Therefore, the total area of the figure is 4+2=6 sq units.
Example 7:
Measure the area of the figure below?

Solution:
Count the no of squares=25
Therefore, the total area of the figure is 25 sq units.
Example 8:
Measure the area of the below figure
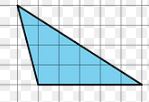
Solution:
No of full squares=5
No of half squares=2 i.e 1 square
No. of squares more than half should be considered as 1. There are 4 such squares
Therefore, the total area of the figure is 5+1+4=10 sq units
FAQs on Measuring the Area with Square Paper
1. Which will measure the surface covered by a two-dimensional object?
The area measures the surface covered by a two-dimensional object.
2. What is the Measurement of the area?
Square units are the measurement of the area.
3. Write the steps for measuring the area using square paper?
- Count the no. of Full Squares
- Count the no. of Half Squares also we know that two triangles make one square.
- If the square is more than half, consider it as 1.
- If the square is less than half, Don’t consider it. Thus we get the area of the figure.
Лабораторная работа Измерению площади плоской фигуры палеткой.
Оборудование:
модели палеток, миллиметровка, модели
фигур, прозрачная бумага, прозрачная
миллиметровка, бумага в клетку 1см на 1
см, карандаши.
Ход
работы:
1.
Рассмотрим различные модели палеток,
прозрачную миллиметровку.
Сделаем
вывод о возможности использования
клетчатой бумаги или обычной миллиметровки
для измерения площади плоской фигуры,
наложением модели фигуры или ее копии
на прозрачном носителе на миллиметровку.
2.
Обведем контур фигуры на листе
миллиметровки.
Измерим
площадь фигуры. Для этого подсчитаем
число квадратных сантиметров лежащих
внутри фигуры. Затем подсчитаем число
квадратных сантиметров, задевающих
фигуру, но не лежащих внутри нее.
3.
Используя формулу
 ,
,
где n
–
число квадратов, целиком лежащих внутри
фигуры, и m
– число квадратов, задевающих фигуру,
но не лежащих внутри нее, подсчитаем
площадь фигуры.
4.
Разделим какой-либо кривой линией данную
фигуру (ее копию на миллиметровке) на
две части, найдем площадь каждой части
и сумму площадей этих частей. Сравним
результат с площадью всей фигуры.
5.
Возьмем в качестве единичного квадрата
четверть квадратного сантиметра и
выполним все операции из пунктов 2-3.
Сравним полученный результат с
первоначальным.
6.
Проделаем операции, указанные в пунктах
2-3, еще дважды.
Сравним результаты трех измерений между
собой.
При
выполнении лабораторной работы возникает
ряд вопросов. Вот некоторые из них:
-
Зависит
ли площадь фигуры от ее положения на
плоскости?
Или,
иначе говоря, если сдвинуть фигуру и
изменить ее положение на плоскости
относительно сети квадратов, изменится
ли площадь фигуры? Или еще иначе, имеют
ли равные фигуры равные площади?
Интуиция,
наглядные представления о площадях
подсказывают положительный ответ на
этот вопрос. К такому же выводу приводят
и строгие рассуждения. Реально же мы
получаем противоположный результат.
Меняя положение фигуры относительно
сети квадратов (пункт 6 ) получаем, что
одна и та же фигура имеет разные числовые
значения площади при одной и той же
единице площади. -
Если
фигуру разбить на несколько частей, то
как связаны между собой площадь всей
фигуры и площади ее частей?
Интуиция,
наглядные представления о площадях
подсказывают, что площадь фигуры равна
сумме площадей ее частей. К такому же
выводу приводят нас и строгие рассуждения.
А на деле сумма площадей частей фигуры(
см. пункт 4) отличается от ее площади,
найденной в пункте 3. -
Что
произойдет с площадью, если изменить
единичный отрезок?
Интуиция
и здесь подсказывает, что площади всех
фигур изменяются “одинаково”, т.е.
площадь каждой фигуры при “новой”
единице измерения длины будет равна
площади этой фигуры при “старой”
единице длины, умноженной на одно и то
же число. К такому же выводу нас приведут
и строгие рассуждения. В пункте 5
лабораторной работы получилось не так.
Почему
же, выполняя лабораторную работу по
нахождению площади фигуры с помощью
палетки, мы видим, что эти очевидные
свойства площади не выполняются. Причина
такого положения в приближенном характере
измерения площади с помощью палетки. С
помощью палетки мы получаем площади
входящих и объемлющих многоугольников
(фигур, составленных из квадратов
определенного ранга), а не собственно
площадь измеряемой фигуры. Искомая
площадь есть предел последовательности
площадей, получаемых в процессе измерения
с помощью все более мелкой палетки. А
ее значение при выбранной единице
площади не зависит ни от способа наложения
палетки, ни от способа разбиения фигуры
на части. Если же выбрать другую единицу
площади, то значение искомой площади
изменится – умножится на определенное
число.
Соседние файлы в папке величина
- #
- #
- #
- #
- #
- #
- #
- #
Простой способ изобразить площадь круга – нарисовать его на миллиметровке. Площадь круга будет примерно равна числу квадратов внутри круга, умноженному на площадь каждого квадрата. Это только приблизительное значение, потому что окружность круга пересекает некоторые квадраты. Вы получите более близкое приближение, если посчитаете количество неполных квадратов, а также количество полных квадратов внутри круга. Это приводит к тому, что довольно легко определить значение числа пи.
-
Используйте миллиметровку с меньшими квадратами, чтобы получить более точный подсчет площади круга с радиусом 1 дюйм.
Нарисуйте круг с радиусом один дюйм на миллиметровой бумаге. Подсчитайте количество квадратов целого графа внутри круга. Умножьте это число на размер каждого квадрата. Подсчитайте количество неполных квадратов, умножьте количество частичных квадратов на размер каждого квадрата и разделите это число на 2. Добавление чисел, полученных вами в обоих расчетах, даст вам приблизительную площадь круга. Круг с радиусом 1 дюйм имеет площадь приблизительно 3, 14 квадратных дюйма.
Удвойте радиус, на этот раз рисуя круг с радиусом 2 дюйма. Этот круг имеет площадь около 12, 5 квадратных дюймов. Снова удвойте радиус, рисуя круг с радиусом 4 дюйма. Площадь этого круга составляет около 50, 25 квадратных дюймов. Удвоение радиуса увеличивает площадь круга в четыре раза.
Разделите область самого большого круга на область самого маленького круга: 50.25 / 3.14 = 16. Радиус этого круга был 4, а 16 – это квадрат 4. Разделите область среднего круга на область самого маленького круга: 12, 5 / 3, 14 = 4. Радиус этого круга был 2, а 4 – квадрат 2.
Поместите это в формулу по-другому. Площадь круга с радиусом 1, умноженная на квадрат любого радиуса, дает площадь круга с этим радиусом. Площадь круга с радиусом 1 является постоянной величиной, и ей было присвоено имя pi. Таким образом, у нас есть формула для площади круга: пи умноженный на квадрат радиуса.
