Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Рассчитать площадь прямоугольника с подробным решением. Калькулятор находит площадь по формуле через длину и ширину прямоугольника. Основные способы и объяснение формул, по которым вы сможете самостоятельно решить свои задачи.
Онлайн-калькулятор площади прямоугольника
Вначале давайте разберемся с определением. У прямоугольника есть 4 стороны. Каждая сторона равна противоположной и параллельна ей. Здесь важно понимать, что все 4 стороны не могут быть равны, иначе получится квадрат. В прямоугольнике будут 2 одинаковые стороны одной длины и 2 одинаковые другой.
Все 4 угла, находящиеся внутри прямоугольника, — прямые. То есть каждый угол равен 90°.
Формула площади прямоугольника через его стороны
Чтобы найти площадь SS прямоугольника, нужно перемножить две его стороны: сторону aa умножаем на сторону bb.
S=a⋅b.S = a cdot b.
У нас есть прямоугольник ABCDABCD. Одна его сторона ABAB равна 55 см, вторая BCBC равна 33 см. Нам нужно найти его площадь SS.
Решение:
Чтобы найти площадь SS, нужно умножить сторону ABAB на сторону BCBC и получаем: S=5⋅3S = 5 cdot 3.
Ответ: S=15S = 15 см2.
Формула площади прямоугольника через диагонали
Площадь прямоугольника можно также рассчитать, зная длину диагоналей и острый угол между ними:
S=12d2sinα.S = frac {1}{2}d^2 sin alpha.
Помним, длины диагоналей в прямоугольнике равны и при пересечении делятся пополам.
Дан прямоугольник ABCDABCD. Его диагональ ACAC равна 88 см, а острый угол между диагоналями 30°30°. Найдите площадь фигуры.
Используем приведенную выше формулу и получаем:
S=12⋅82⋅sin30∘=12⋅64⋅12=644=16S = frac{1}{2} cdot 8^2 cdot sin 30^{circ} = frac{1}{2} cdot 64 cdot frac{1}{2} = frac{64}{4} = 16
Ответ: S=16S = 16 см2.
Не знаете, как решить задачу по геометрии онлайн? Оформите заказ на Студворк!
Тест по теме «Площадь прямоугольника»
Площадь прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем, как вычислять площадь прямоугольника.

Различные формулы вычисления площади (а их действительно немало), изучают в 8 классе школы.
Что такое площадь прямоугольника
Но для начала давайте все-таки дадим основные определения:
Прямоугольник – это геометрическая фигура, относящаяся к категории четырехугольников. Ее отличительная особенность в том, что противоположные стороны лежат на параллельных прямых (то есть параллельны друг другу) и равны.
Прямоугольник является параллелограммом (что это такое?) и выглядит вот так:

А частным случаем прямоугольника, если у него все стороны равны между собой, является квадрат.
Площадь любой геометрической фигуры, формально говоря, это ее размер. Другими словами, размер того пространства, которое находится внутри границ фигуры.
В отношении четырехугольников применимо еще понятие «квадратура». С его помощью показывали, сколько квадратов вместится внутрь фигуры.
Собственно, отсюда и пошло современное обозначение площадей, когда речь идет о габаритах помещения или какой-то территории. Мы часто слышим «столько-то квадратных метров (миллиметров, сантиметров, километров)» или просто «столько-то квадратов».

Для площади геометрических фигур действуют определенные правила:
- Она не может быть отрицательной.
- У равных фигур всегда равные площади.
- Если две фигуры не пересекаются друг с другом, то их общая площадь равна сумме площадей фигур по отдельности.
- Если одна фигура вписана в другую, то ее площадь всегда меньше, чем у второй.
Обычно фигуры, которые имеют равные площади, называют «равновеликими».
Как найти площадь прямоугольника
Площадь прямоугольника вычисляется по очень простой формуле – надо лишь перемножить его стороны.
Возьмем, к примеру, такой прямоугольник:
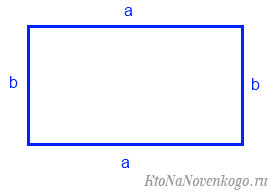
Площадь геометрической фигуры обычно обозначается латинской буквой «S». И тогда формула для конкретного примера будет:
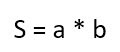
Например, если мы имеем прямоугольник со сторонами 2 и 3 сантиметра, то его площадь составит 2 * 3 = 6 сантиметров.
Но бывают случаи, когда неизвестны размеры сторон прямоугольника, а площадь вычислить все равно надо. Для этого существуют более сложные формулы.
Формула площади прямоугольника через периметр
Если известна длина только одной стороны, но известен еще и периметр прямоугольника.
В этом случае есть два варианта.
- Первый — вычислить длину второй стороны. Для этого надо вспомнить, что периметр (обозначается буквой «Р») считается по формуле:
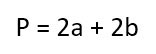
И тогда обратные расчеты выглядят вот так:
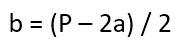
Ну а после того, как станет известна длина второй стороны прямоугольника, можно прибегнуть к классической формуле.
- Ну и второй вариант – воспользоваться сразу готовой формулой:
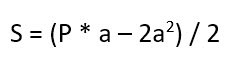
Площадь прямоугольника через диагональ
-
Известна одна сторона и длина диагонали.
Тут опять же есть два варианта. В первом случае вычисляем длину второй стороны, используя теорему Пифагора.
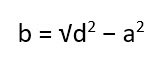
Второй вариант – опять же сразу прибегнуть к готовой формуле:
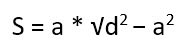
-
Если известны длина диагоналей и угол между ними.
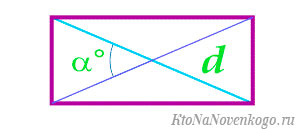
В этом случае стоит воспользоваться вот такой формулой:
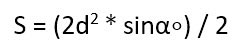
Вот и все, что нужно знать о вычислении площади прямоугольников.
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
Пусть `A`, `B` и `C` – углы треугольника`ABC`; `a`, `b` и `c` – противолежащие этим углам стороны; `h_a`, `h_b` и `h_c` – высоты к этим сторонам; `r` – радиус вписанной окружности;`R` – радиус описанной окружности; `2p=(a+b+c)` – периметр треугольника; `S` – площадь треугольника
| `S=1/2ah_a=1/2bh_b=1/2ch_c`, | (1) |
| `S=1/2 ab sinC=1/2acsinB=1/2bcsinA`, | (2) |
| `S=pr`, | (3) |
| ``S=sqrt(p(p-a)(p-b)(p-c))` – формула Герона, | (4) |
| `S=(abc)/(4R)`. | (5) |
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
`R=(abc)/(4S)=(13*14*15)/(4*84)=65/8=ul(8,125)`.
Для треугольника `KLM` вычисленная по формуле Герона затруднительны, более простой путь – найти косинус, например, угла `M`. По теореме косинусов
`13=14+15-2sqrt(14)*sqrt(15)cosM iffcosM=8/(sqrt(14)*sqrt(15))`,
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
`S_(KML)=1/2KM*LMsinM=1/2*(sqrt(14)*sqrt(15)*sqrt(146))/(sqrt(14)*sqrt(15))=(sqrt(146))/2`,
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.{1}^{○}$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
`(S_(DBC))/(S_(ABC))=(DC)/(AC)`.
$$ 2.{2}^{○}$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
`(S_(KBL))/(S_(ABC))=(BK*BL)/(BA*BC)`.
$$ 2.{3}^{○}$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC~DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Известно, что три медианы треугольника пересекаются в одной точке и делятся в отношении `2:1`, считая от вершины. Пусть `O` – точка пересечения медиан треугольника `DeltaABC` площади `S` (рис. 7а). Надо доказать, что площади всех шести треугольников с верш иной в точке `O`, составляющих треугольник `ABC`, равны между собой, т. е. равны `1/6S`.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Точка `M` – середина стороны `BC` (рис. 7б), по утверждению $$ 2.{1}^{○}$$ о сравнении площадей `S_(ABM)=1/2S`. Медиана `BN`, пересекая медиану `AM` в точке `O` (рис. 7в), делит её в отношении `AO:OM=2:1`, т. е. `OM=1/3AM`. По тому же утверждению $$ 2.{1}^{○}$$ площадь треугольника `BOM` составляет `1//3` площади треугольника `ABM`, т. е.
`S_(BOM)=1/3(1/2S)=1/6S`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
1. Обозначим `S_(ABC)=S`, `S_(DBKO)=sigma` и `S_(ADO)=a`. По утверждению $$ 2.{1}^{○}$$ имеем `S_(ABK)=a+sigma=3/5S` (так как `BK:BC=3:5`). Площадь `a` треугольника `ADO` найдём как часть площади треугольника `ADC`, зная, что `S_(ADC)=1/3S` (так как `AD:AB=1:3`).
2. Через точку `D` проведём прямую `DL“||“AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL“||“AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK“||“DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
`22/45`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
Пусть `O` – точка пересечения медиан треугольника `ABC` (рис. 10) и пусть `m_a=AM=3`, `m_b=BN=4` и `m_c=CP=5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
Итак, `S=3`, `S_1=8`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
Из решения предыдущей задачи следует, что `S_(OCD)=S_1=1/3S` (здесь `S` – площадь треугольника `ABC`). Кроме того, площади подобных треугольников относятся как квадраты сходственных сторон, поэтому `(S_1)/(S_0)=(2/3)^2`. Таким образом, имеем `S_0=9/4S_1=3/4S`, т. е.
`S_(m_am_bm_c)=3/4S_(abc)`.
Из рассуждений в решении Примера 9 следует, что всегда существует треугольник со сторонами, равными медианам данного треугольника, поскольку всегда существует подобный ему треугольник со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`. Кроме того, становится ясным план построения треугольника по трём отрезкам, равным его медианам: сначала строится треугольник `OCD` (см. рис. 10) со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`, затем точка `N` – середина отрезка `OD`, потом точка `A` (из `AN=NC`) и точка `B` (из `OB=OD`). Это построение осуществимо, если существует треугольник `OCD`, т. е. если существует треугольник со сторонами `m_a`, `m_b`, `m_c`. Итак, вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
`S=pr=(14+1)*sqrt3=15sqrt3`.
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
`x=(2ab)/(a+b)cos varphi/2`.
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Центр окружности `I_a` лежит на пересечении биссектрисы угла `A` и биссектрис внешних углов при вершинах `B` и `C`. Легко видеть, что если `D`, `F` и `E` – точки касания, то `I_aD=I_aF=I_aE=r_a`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
`S_(ABC)=S_(ABI_a)+S_(ACI_a)-S_(BCI_a)=1/2 cr_a+1/2br_a-1/2ar_a=`
`=r_a (c+b-a)/2=r_a(2p-2a)/2=r_a(p-a)`.
Итак,
Калькулятор для расчета площади
Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
|
|
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
Способ нахождения площади треугольника:
| a= |
|
| b= | |
|
c= |
Вычислить
Рассчитать площадь круга, если известен:
| r= |

|
Вычислить
Способ нахождения площади параллелограмма:
| a= |

|
|
h=
|
|
Вычислить
Рассчитать площадь сектора круга, если известен:
|
r= |

|
|
θ= |
Вычислить
Способ нахождения площади трапеции:
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.
| Метрические единицы измерения площади: | |
| Квадратный метр, производная единица системы СИ 1 м2 = | 1 са (сантиар) |
| Квадратный километр – 1 км2 = | 1 000 000 м2 |
| Гектар – 1 га = | 10 000 м2 |
| Ар (сотка) – 1 а = | 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м) |
| Квадратный дециметр, 100 дм2 = | 1 м2; |
| Квадратный сантиметр, 10 000 см2 = | 1 м2; |
| Квадратный миллиметр, 1 000 000 мм2 = | 1 м2. |
Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.
