Как найти площадь полигона по координатам

Площадь
полигона S
по координатам его вершин вычисляется
по формулам (1.14):

(1.14)

где
x_i
, y_i
– координаты i
– ой вершины полигона;

x_i+1
, y_i+1
– координаты последующей i+1
вершины полигона;

x_i-1
, y_i-1
– координаты предыдущей i
– 1 вершины полигона;

n
– число вершин в полигоне.

Таблица 1.4

Определение площади
полигона по координатам

1.5 Определение площадей участков на планах.

Наиболее
распространенным и достаточно точным
способом определения площадей участков,
имеющих криволинейные контуры, является
измерение площадей планиметром.

Перед измерением
площадей планиметр поверяют и, если
есть необходимость, юстируют.

Затем
определяют цену деления каретки
планиметра. Для этого, на листе плана
устанавливают иглу планиметра в любую
точку замкнутого контура, площадь
которого известна: полигона, квадрата
сетки квадратов, окружности известного
радиуса и т д. берут отсчет по каретке
( если у планиметра одна каретка) или
по обеим кареткам планиметра. Затем
обводят контур по часовой стрелке,
возвращая иглу в исходную точку, и вновь
берут отсчеты.

При работе с
однокареточным планиметром площадь
контура обводят дважды, а при работе с
двухкареточным планиметром один раз.
Цену деления у однокареточного планиметра
р определяют по формуле (1.15):

Р=
S_изв/(n_к-n_н)ср
; (1.15)

Где
S_изв
– известная площадь контура ;

n_к
, n_н–
соответственно конечный и начальный
отсчеты по каретке ;

(n_к-n_н)ср
– среднее значение разности отсчетов
из первого и второго обводов контура.

Цена
деления у двухкаретного планиметра
определяется как, среднее арифметическое
из цены деления по первой и второй
кареткам. Для измерения площади контура
полюс планиметра устанавливают вне
контура, а иглу в любую точку контура.
Затем берут начальный отсчет (при
однокареточном планиметре) по каретке,
обводят контур по часовой стрелке.
Возвращая иглу в исходную точку, и снова
берут отсчет по каретке. Затем повторно
обводят этот же контур, записывая отсчеты
в таблицу. Площадь контура вычисляют
по формуле (1.16):

S_i=p*(n_ik
–
n_iн)ср,
(1.16),

где
(n_ik
– n_iн)ср
–среднее значение разности отсчетов
из первого и второго обводов i-го
контура.

При измерении
площадей планиметром необходимо
выполнять следующие требования:

• не
  допускать, чтобы угол между рычагами
  планиметра был меньше 30° или больше
  150°,

• не
  допускать схода обводного колесика с
  листа бумаги.

Таблица 1.7

Ведомость вычисления
площадей участков угодий

двухкаретным
планиметром ПП-2К

Сумма
измеренных площадей должна равняться
теоретической сумме площади полигона.
Из-за неизбежных погрешностей будет
невязка:

ΔS
=S_план
–
S_коор,

Где
S_план
–сумма площадей участков, вычисленная
по показаниям планиметра;

S_коор
– площадь полигона, вычисленная по
координатам;

Относительная
невязка вычисляется по формуле (1.17):

ΔS
=( ΔS/S_коор)
=

Если
Δ не превышает 1/120, то считают точность
измерения площадей планиметром
удовлетворительной. В этом случае
находят поправку на измеренные планиметром
площади участков, для чего невязку
распределяют на площади участков
пропорционально их площадям. Если же
относительная ошибка больше допустимой,
измерение площадей участков повторяют
заново.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 января 2022 года; проверки требуют 2 правки.

Формула площади Гаусса (формула землемера или формула шнурования или алгоритм шнурования) — формула определения площади простого многоугольника, вершины которого заданы декартовыми координатами на плоскости. В формуле векторным произведением координат и сложением определяется площадь области, охватывающей многоугольник, а затем из нее вычитается площадь окружающего многоугольника, что дает площадь многоугольника внутри. Также она называется формулой шнурования, так как положительные и отрицательные слагаемые, состоящие из перемножаемых координат, располагаются крест-накрест, как при завязывании шнурков. Она находит применение в геодезии, лесном хозяйстве и других областях.

Формула была описана Мейстером (1724—1788) в 1769 году и Гауссом в 1795 году. Она может быть проверена путём деления многоугольника на треугольники, но её также можно рассматривать как частный случай теоремы Грина.

Формула определения площади определяется путём взятия каждого ребра многоугольника АВ и вычисления площади треугольника АВО с вершиной в начале координат О через координаты вершин. При обходе вокруг многоугольника образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника. Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется, если она слева, и вычитается, если она справа с точки зрения из начала координат.

Формула площади верна для любого самопересекающегося многоугольника, который может быть выпуклым или вогнутым.

Определение[править | править код]

Формула может быть представлена следующим выражением:

где

S — площадь многоугольника,

n — количество сторон многоугольника,

(x_i, y_i), i = 1, 2, …, n — координаты вершин многоугольника.

Другое представление этой же формулы^[1][2]:

где

x_n+1 = x₁, x₀ = x_n,

y_n+1 = y₁, y₀ = y_n.

Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны, и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, то детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина.

Примеры[править | править код]

Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости. Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую координату x первой вершины и умножим её на координату y второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определён по следующей формуле^[3]:

где x_i и y_i обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3.

Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x₅ и y₅:

S для четырехугольника — переменные до x₄ и y₄:

Более сложный пример[править | править код]

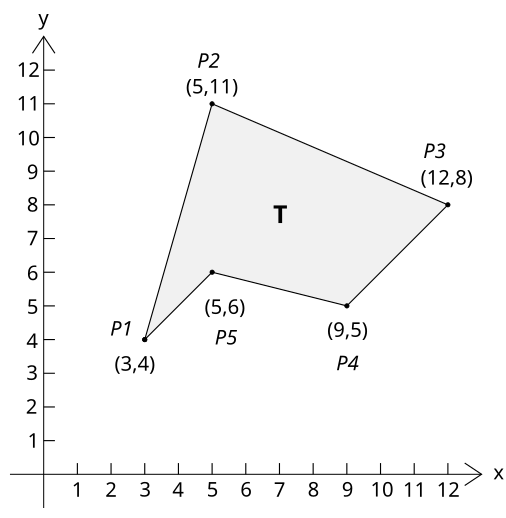
Рассмотрим многоугольник, представленный на рисунке и заданный точками (3, 4), (5, 11), (12, 8), (9, 5), (5, 6):

Площадь этого многоугольника:

Объяснение названия[править | править код]

Формула называется «формулой шнурков» из-за общего метода, используемого для её вычисления. Этот метод использует матрицу. В качестве примера возьмём треугольник с вершинами (2, 4), (3, −8), (1, 2). Затем построим следующую матрицу, «обходя вокруг» треугольника и заканчивая начальной точкой:

Сначала проведём диагональ вниз и вправо косой чертой, как показано ниже:

и перемножим пары чисел, соединённых чертой, а затем сложим все суммы:

(2 × −8) + (3 × 2) + (1 × 4) = −6.

Сделаем то же самое, проводя косую черту по диагонали вниз и влево, как показано ниже:

(4 × 3) + (−8 × 1) + (2 × 2) = 8.

Затем вычтем сумму второй группы из первой и возьмём модуль:

|(−6) − (8)| = 14.

Деление результата на два даёт площадь.
Организация чисел в матрицу с диагональными линиями упрощает запоминание формулы.
В результате проделанной операции с рисованием диагональных (косых) линий матрица с числами напоминает зашнурованную обувь, отсюда и происходит название «алгоритма шнурования».

Хорошее описание “Шнуровки Гаусса” представлено в видео на канале Wild Mathing [1]

См. также[править | править код]

• Планиметр
• Теорема Грина

Примечания[править | править код]

ТЕМА: Определение площади полигона по координатам его вершин.

ЦЕЛЬ: Определить площадь полигона аналитическим методом.

ИСХОДНЫЕ ДАННЫЕ:

1. Координаты
вершин полигона

2. Направление
измерения углов полигона (правые).

ОБЕСПЕЧЕНИЕ:

1.       Калькулятор.

2.       Инструкционная карта.

3.       Каталог координат.

Полигоном называют территорию, ограниченную замкнутым
теодолитным ходом. При известных координатах вершин теодолитного хода площадь
полигона или любой фигуры ограниченной прямыми линиями можно вычислить по двум
формулам:

Удвоенная площадь полигона равна сумме произведений абсциссы
каждой точки на разность ординат последующей и предыдущей точек.

Она же (удвоенная площадь) равна сумме произведений каждой
ординаты на разность абсцисс предыдущей и последующей точек.

2S = x₁(y₂-y₃)+x₂(y₃-y₁)+x₃(y₁-y₂)

2S = y₁(x₃-x₂)+y₂(x₁-x₃)+y₃(x₂-x₁)

                                                2
(x₂,
y₂)

                       1(x₁,
y₁)                                   
3 (x₃,
y₃)

СОДЕРЖАНИЕ И ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ РАБОТЫ:

1. В ведомость
вычисления площади полигона в графу 1 занести номера вершин хода.

2. В графы 2, 3
занести координаты по осям х и у.

3. Графы 4, 5
вычислить по формулам:

Δх_i = х _пред – х_посл 
или  Δх_i = х _i-1 – х _i+1

Δу_i = у _посл – у_пред 
или  Δу_i = у _i+1 – у _i-1

4.
Подбить суммы граф 4, 5, (Суммы должны равняться нулям).

5.
Графы 6, 7 вычислить по формулам:

х_i* Δу_i   или   х_i (у _i+1 – у _i-1)

 у_i * Δх_i      или     у_i (х _i-1 – х _i+1)

6.
Найти среднее значение удвоенной площади полигона и определить площадь полигона
в гектарах.

2S
= Σ (х_i*
Δу_i)
= Σ (х_i
(у _i+1
– у
_i-1))

2S
= Σ (у_i *
Δх_i)=
Σ (у_i (х _i-1 –
х _i+1))

Таблица
1- Ведомость вычисления площади полигона по координатам его вершин.

            Схема
полигона                                S= 2S_ср/2=_________________________

                                                                  
_________________________

Вывод:______________________________________________________________________________________________________________________________________________________________________________________

Выполнил:__________________________

Инструкция по использованию калькулятора

Координаты вершин полигона (широту и долготу) следует указывать в градусах в виде десятичной дроби. Координаты вершин указываются последовательно и в одном направлении (по часовой или против часовой стрелки).