Как рассчитать площадь поверхности конуса
На данной странице калькулятор поможет рассчитать площадь поверхности конуса онлайн. Для расчета задайте высоту, радиус или образующую.
Конус – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.
Образующая конуса – это отрезок, соединяющий вершину и границу основания.
Боковая поверхность через радиус и образующую
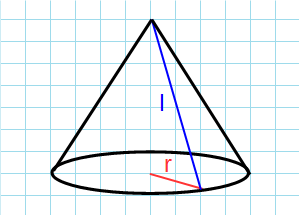
Формула боковой поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Боковая поверхность через радиус и высоту
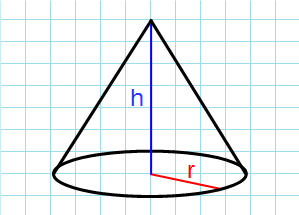
Формула боковой поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Полная площадь через радиус и образующую

Формула площади полной поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Полная площадь через радиус и высоту

Формула полной площади поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Конус — это совокупность всех лучей, которые исходят из какой-либо точки пространства и пересекают плоскую поверхность.
Онлайн-калькулятор площади поверхности конуса
Точка, которая является началом этих лучей, называется вершиной конуса. В случае когда в основании конуса лежит многоугольник, конус превращается в пирамиду.
Конус состоит из некоторых элементов, знать которые необходимо для решения задач.
Образующая — отрезок, соединяющий точку, лежащую на окружности круга, который является основанием, и вершину конуса.
Высота — расстояние от плоскости основания до точки вершины конуса.
Виды конуса
Конус может быть нескольких видов:
Прямым, если его основанием является эллипс или круг. Причем вершина должна точно проектироваться в центр основания.
Косым — это тот случай, когда центр фигуры, лежащей в основании, не совпадает с проекцией вершины на это основание.
Круговым — соответственно, если основание — круг.
Усеченным — область конуса, которая будет лежать между основанием и сечением плоскости, параллельной основанию и пересекающей этот конус.
Формула площади поверхности конуса
Для нахождения полной площади поверхности конуса нужно найти сумму площади основания (или оснований, если конус усеченный) конуса и площади его боковой поверхности:
S=Sосн+SбокS=S_{text{осн}}+S_{text{бок}}
SоснS_{text{осн}} — площадь основания (оснований) конуса;
SбокS_{text{бок}} — площадь боковой поверхности конуса.
Рассмотрим примеры нахождения площади поверхности обычного прямого кругового конуса, а также усеченного этого же конуса.
Формула площади поверхности кругового конуса
Sосн=π⋅r2S_{text{осн}}=picdot r^2
Sбок=π⋅r⋅lS_{text{бок}}=picdot rcdot l
rr — радиус круга (основания) кругового конуса;
ll — длина образующей этого конуса.
Найти площадь поверхности кругового конуса, если радиус основания равен 3 (см.), а высота hh треугольника, путем вращения которого образовался данный конус, равна 4 (см.)
Решение
r=3r=3
h=4h=4
Образующую можно найти, если рассмотреть треугольник, катетами которого являются радиус и высота, а гипотенузой – сама образующая ll. По теореме Пифагора имеем:
l2=r2+h2l^2=r^2+h^2
l2=32+42l^2=3^2+4^2
l2=25l^2=25
l=5l=5
Вычислим площадь основания конуса:
Sосн=π⋅r2=π⋅32≈28.26S_{text{осн}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅r⋅l=π⋅3⋅5≈47.10S_{text{бок}}=picdot rcdot l=picdot 3cdot 5approx47.10 (см. кв.)
Полная площадь
S=Sосн+Sбок≈28.26+47.10=75.36S=S_{text{осн}}+S_{text{бок}}approx28.26+47.10=75.36 (см. кв.)
Ответ: 75.36 см. кв.
Формула площади поверхности усеченного кругового конуса
Для усеченного кругового конуса площадь боковой поверхности можно найти по формуле:
Sбок=π⋅l⋅(r+r′)S_{text{бок}}=picdot lcdot (r+r’)
ll — длина образующей конуса;
rr — радиус основания;
r′r’ — радиус круга, получаемый при усечении кругового конуса.
Условие возьмем из предыдущей задачи, добавив к нему только лишь радиус второго основания r′r’. Пусть он будет равен 2 (см.). Требуется вычислить полную площадь поверхности этого усеченного конуса.
Решение
l=5l=5
r=3r=3
r′=2r’=2
Оснований у нас теперь два, поэтому полная площадь оснований будет равна сумме площадей этих оснований с радиусами rr и r′r’:
Sосн=Sосн r+Sосн r’S_{text{осн}}=S_{text{осн r}}+S_{text{осн r’}}
Площадь основания радиуса rr:
Sосн r=π⋅r2=π⋅32≈28.26S_{text{осн r}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь основания радиуса r′r’:
Sосн r’=π⋅r′2=π⋅22≈12.56S_{text{осн r’}}=picdot r’^2=picdot 2^2approx12.56 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅l⋅(r+r′)=π⋅5⋅(3+2)≈78.50S_{text{бок}}=picdot lcdot (r+r’)=picdot 5cdot (3+2)approx78.50 (см. кв.)
Полная площадь:
S=Sосн+Sбок=Sосн r+Sосн r’+Sбок≈28.26+12.56+78.50=119,32S=S_{text{осн}}+S_{text{бок}}=S_{text{осн r}}+S_{text{осн r’}}+S_{text{бок}}approx28.26+12.56+78.50=119,32 (см. кв.)
Ответ: 119,32 см. кв.
Не знаете, как решить задачу по геометрии? Наши эксперты оперативно помогут вам с решением!
Тест по теме «Площадь поверхности конуса»
Площадь поверхности конуса состоит из площади боковой поверхности конуса и площади основания (круга).
|
Рис. (1). Конус |
Площадь боковой поверхности конуса вычисляется по формуле: где (R) — радиус конуса, (l) — образующая конуса. Площадь основания конуса вычисляется по формуле S(круга) = Площадь полной поверхности конуса вычисляется по формуле S(полн.) =S(бок.) +S(круга) =πRl+πR2. Объём конуса вычисляют по формуле V = 13⋅H⋅ S(круга) = πR2⋅H3 |
Площадью боковой поверхности конуса является площадь её развёртки.
Развёрткой боковой поверхности конуса является круговой сектор.
|
Рис. (2). Развёртка конуса |
α
— градусная мера центрального угла. Радиус этого сектора — образующая конуса (AK = KB = l)
|
Источники:
Рис. 1. Конус. © Якласс
Рис. 2. Развёртка конуса. © Якласс
Все формулы для площадей полной и боковой поверхности тел
1. Площадь полной поверхности куба

a – сторона куба
Формула площади поверхности куба,(S):
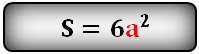
2. Найти площадь поверхности прямоугольного параллелепипеда

a, b, c – стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):

3. Найти площадь поверхности шара, сферы

R – радиус сферы
π ≈ 3.14
Формула площади поверхности шара (S):
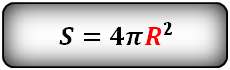
4. Найти площадь боковой и полной поверхности цилиндра
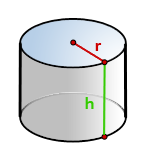
r – радиус основания
h – высота цилиндра
π ≈ 3.14
Формула площади боковой поверхности цилиндра, (Sбок):
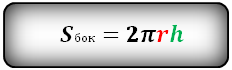
Формула площади всей поверхности цилиндра, (S):

5. Площадь поверхности прямого, кругового конуса
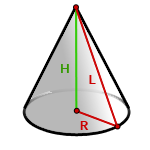
R – радиус основания конуса
H – высота
L – образующая конуса
π ≈ 3.14
Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):

Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):

Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):

Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):

6. Формулы площади поверхности усеченного конуса
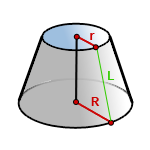
R – радиус нижнего основания
r – радиус верхнего основания
L – образующая усеченного конуса
π ≈ 3.14
Формула площади боковой поверхности усеченного конуса, (Sбок):

Формула площади полной поверхности усеченного конуса, (S):
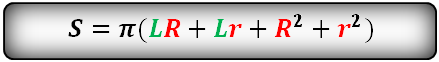
7. Площадь поверхности правильной пирамиды через апофему
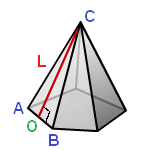
L – апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)
P – периметр основания
Sосн – площадь основания
Формула площади боковой поверхности правильной пирамиды (Sбок):
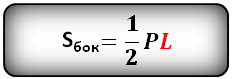
Формула площади полной поверхности правильной пирамиды (S):
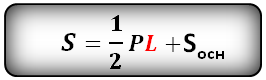
8. Площадь боковой поверхности правильной усеченной пирамиды
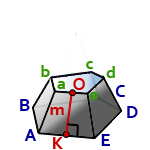
m – апофема пирамиды, отрезок OK
P – периметр нижнего основания, ABCDE
p – периметр верхнего основания, abcde
Формула площади боковой поверхности правильной усеченной пирамиды, (S):
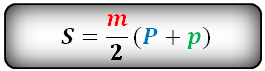
9. Площадь поверхности шарового сегмента

R – радиус самого шара
h – высота сегмента
π ≈ 3.14
Формула площади поверхности шарового сегмента, (S):

10. Площадь поверхности шарового слоя
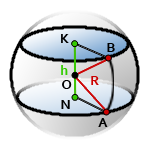
h – высота шарового слоя, отрезок KN
R – радиус самого шара
O – центр шара
π ≈ 3.14
Формула площади боковой поверхности шарового слоя, (S):

11. Площадь поверхности шарового сектора
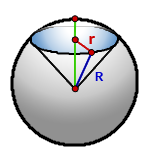
R – радиус шара
r – радиус основания конуса = радиус сегмента
π ≈ 3.14
Формула площади поверхности шарового сектора, (S):

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого кругового конуса (боковую, полную и основания), а также разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади конуса
- 1. Боковая поверхность
- 2. Основание
-
3. Полная площадь
-
Примеры задач
Формула вычисления площади конуса
1. Боковая поверхность
Площадь (S) боковой поверхности конуса равняется произведению числа π на радиус основания и на длину образующей.
Sбок. = πRl

Образующая (l) соединяет вершину конуса и границу основания, другими словами, точку на окружности.
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
Основанием конуса является круг, площадь которого вычисляется так:
Sосн. = πR2
Учитывая то, что диаметр круга равняется двум его радиусам (d = 2R), данную формулу можно представить в виде:
Sосн. = π(d/2)2
3. Полная площадь
Для вычисления суммарной площади конуса следует сложить площади боковой поверхности и основания:
Sполн. = πRl + πR2 = πR(l + R)
Примеры задач
Задание 1
Вычислите площадь боковой поверхности конуса, если известно, что его радиус равен 16 см, а длина образующей – 5 см.
Решение:
Используем соответствующую формулу с известными нам величинами:
S = 3,14 ⋅ 16 см ⋅ 5 см = 251,2 см2.
Задание 2
Высота конуса равна 4 см, а его радиус – 3 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если рассмотреть конус в сечении, то можно заметить, что его высота, радиус и образующая представляют собой прямоугольный треугольник. Следовательно, воспользовавшись теоремой Пифагора, можно найти длину образующей (является гипотенузой):
l2 = (4 см)2 + (3 см)2 = 25 см2.
l = 5 см.
Осталось только использовать найденное и известные по условиям задачи значения, чтобы рассчитать площадь:
S = 3,14 ⋅ 3 см ⋅ (5 см + 3 см) = 75,36 см2.
