В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
-
Формула площади правильной призмы
- 1. Общая формула
-
2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
- Примеры задач
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы
Основание: равносторонний треугольник.
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 3ah |
| полная |  |
microexcel.ru
3. Площадь правильной четырехугольной призмы
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 4ah |
| полная | Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
4. Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 6ah |
| полная |  |
microexcel.ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:

Обозначения
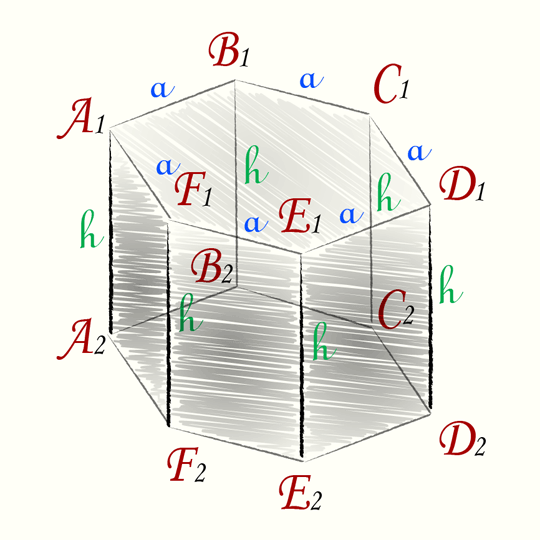
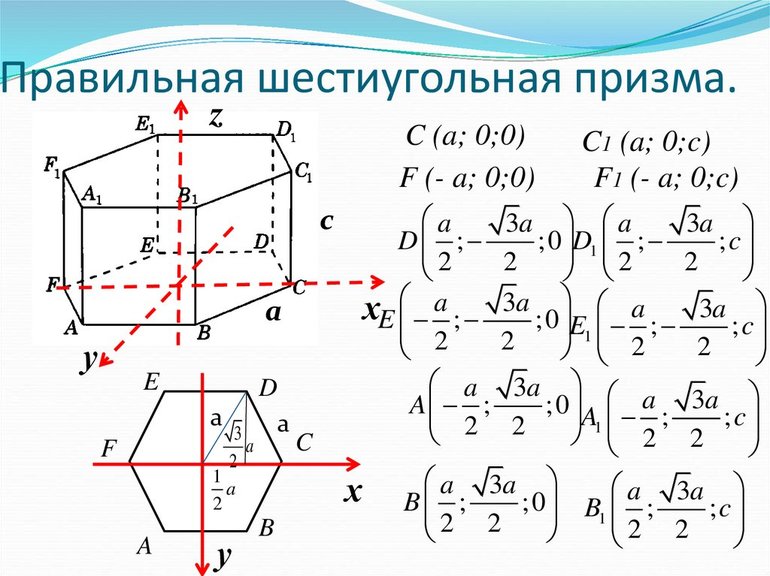
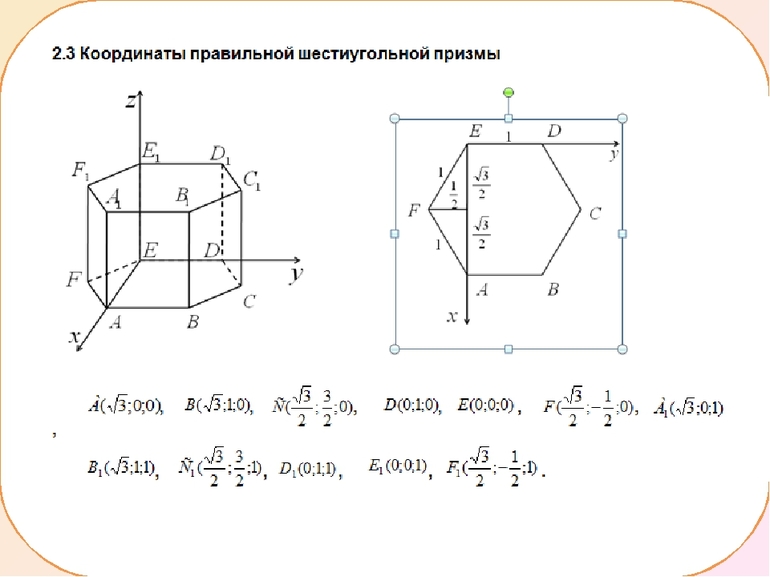
- $ABCDEFA_1B_1C_1D_1E_1F_1$ — правильная шестиугольная призма
- $a$ — длина стороны основания призмы
- $h$ — длина бокового ребра призмы
- $S_{text{осн.}}$ — площадь основания призмы
- $S_{text{бок.}}$ — площадь боковой грани призмы
- $S_{text{полн.}}$ — площадь полной поверхности призмы
- $V_{text{призмы}}$ — объем призмы
Площадь оснований призмы
В основаниях призмы находятся правильные шестиугольники со стороной $a$. По свойствам правильного шестиугольника, площадь оснований призмы равна $$ S_{text{осн.}}=frac{3sqrt{3}}{2}cdot a^2 $$ Таким образом, получается, что $S_{ABCDEF}=S_{A_1B_1C_1D_1E_1F_1}=frac{3sqrt{3}}{2}cdot a^2$.
Площадь полной поверхности призмы
Площадь полной поверхности призмы складывается из площадей боковых граней призмы и площадей ее оснований. Каждая из боковых граней призмы является прямоугольником со сторонами $a$ и $h$. Следовательно, по свойствам прямоугольника $$ S_{text{бок.}}=acdot h $$ У призмы шесть боковых граней и два основания, следовательно, площадь ее полной поверхности равна $$ S_{text{полн.}}=6cdot S_{text{бок.}}+2cdot S_{text{осн.}}=6cdot acdot h+2cdot frac{3sqrt{3}}{2}cdot a^2$$
Объем призмы
Объем призмы вычисляется как произведение площади ее основания на ее высоту. Высотой правильной призмы является любое из ее боковых ребер, например, ребро $AA_1$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{text{призмы}}=S_{text{осн.}}cdot AA_1=frac{3sqrt{3}}{2}cdot a^2cdot h $$
Правильный шестиугольник в основаниях призмы

Находим $EA_1$

- $AA_1=h$
- $AE=sqrt{3}cdot a$ — как мы только что выяснили
- $angle EAA_1=90^{circ}$ — по свойствам правильной призмы
Таким образом, получается, что треугольник $AEA_1$ прямоугольный. По свойствам прямоугольного треугольника $$ EA_1=sqrt{AA_1^2+AE^2}=sqrt{h^2+3cdot a^2} $$ Если $h=a$, то тогда $$ EA_1=2cdot a $$ После аналогичных рассуждений получаем, что $FB_1=AC_1=BD_1=CE_1=DF_1=sqrt{h^2+3cdot a^2}$.
Находим $EB_1$

- $BB_1=h$
- $BE=2cdot a$ — потому что $EO=OB=a$
- $angle EBB_1=90^{circ}$ — по свойствам правильной призмы
Таким образом, получается, что треугольник $BEB_1$ прямоугольный. По свойствам прямоугольного треугольника $$ EB_1=sqrt{BB_1^2+BE^2}=sqrt{h^2+4cdot a^2} $$ Если $h=a$, то тогда $$ EB_1=sqrt{5}cdot a $$ После аналогичных рассуждений получаем, что $FC_1=AD_1=BE_1=CF_1=DA_1=sqrt{h^2+4cdot a^2}$.
Находим $OF_1$

- $FF_1=h$
- $FO=a$
- $angle OFF_1=90^{circ}$ — по свойствам правильной призмы
Таким образом, получается, что треугольник $FOF_1$ прямоугольный. По свойствам прямоугольного треугольника $$ OF_1=sqrt{FF_1^2+OF^2}=sqrt{h^2+a^2} $$ Если $h=a$, то тогда $$ OF_1=sqrt{2}cdot a $$ После аналогичных рассуждений получаем, что $OA_1=OB_1=OC_1=OD_1=OE_1=sqrt{h^2+a^2}$.
Находим $FE_1$

- $EE_1=h$
- $FE=a$
- $angle FEE_1=90^{circ}$ — по свойствам правильной призмы
Таким образом, получается, что треугольник $FEE_1$ прямоугольный. По свойствам прямоугольного треугольника $$ FE_1=sqrt{FE^2+EE_1^2}=sqrt{h^2+a^2} $$ Если $h=a$, то тогда $$ FE_1=sqrt{2}cdot a $$ После аналогичных рассуждений получаем, что длины диагоналей остальных боковых граней призмы также равны $sqrt{h^2+a^2}$.
Площадь правильной шестиугольной призмы
Правильная шестиугольная призма — это прямая призма основанием которой служит правильный шестиугольник.
Площадь правильной шестиугольной призмы
Как мы видим — призма имеет два основания, эти основания правильные шестиугольники со стороной a, и шесть боковых сторон, которые представляют из себя прямоугольники со сторонами a и h
Площадь правильной шестиугольной призмы складывается из двух площадей оснований и шести площадей боковых граней.
[ S_{призмы} = 2S_{осн} + 6S_{бок} ]
Подставим сюда формулу площади прямоугольника и формулу площади правильного шестиугольника и получим:
[ S_{призмы} = 2frac{3sqrt{3}}{2}a^2 + 6ah ]
или
[ S_{призмы} = 3a(sqrt{3}a + 2h) ]
Вычислить, найти площадь правильной шестиугольной призмы по формуле (3)
Площадь правильной шестиугольной призмы |
стр. 334 |
|---|
A hexagonal prism is a three-dimensional geometric structure with two hexagonal bases connected by six rectangular faces. It is a polyhedron with eight faces, twelve vertices, and eighteen edges. It is also known as an octahedron as it has eight faces; two of the eight faces are hexagons, which are the bases of the prism, and the other six faces are rectangles, which are the lateral (or) side faces of the prism. The top and bottom faces of the hexagonal prism are in the shape of a hexagon and are congruent with each other.
There are two kinds of hexagonal prisms, namely, a regular hexagonal prism and an irregular hexagonal prism.
- A regular hexagonal prism is a prism that has two hexagonal bases whose all sides are of the same length. In a regular hexagonal prism, the angles also measure the same.
- An irregular hexagonal prism is a prism that has two irregular hexagonal bases. All the sides of the base do not have the same length, and the measures of each angle are different.
Surface Area of a Hexagonal Prism
The total area that is covered by the surfaces of a hexagonal prism is referred to as its surface area. The surface area of a prism is measured in terms of square units such as sq. m, sq. cm, sq. in, etc. A hexagonal prism has two types of areas just like other three-dimensional shapes: lateral surface area (LSA) and total surface area (TSA).
Let us consider a hexagonal prism that has an apothem length “a”, a base length “s”, and a height “h”. We know that the general formula to calculate the lateral surface area of a prism is the product of its base and height. So, the lateral surface area of the prism of a hexagonal prism is determined by calculating the product of the perimeter of the base of the hexagonal prism and its height.
The formula to determine the lateral surface area of the hexagonal prism is equal to the sum of the areas of its six rectangular faces. Thus,
Lateral surface area of hexagonal prism (LSA) = 6sh sq. units.
Where “s” is the length of the base edge, and
“h” is the height of the prism.
The formula to determine the surface area of a hexagonal prism is given as follows:
Total Surface Area, TSA = 2×(Area of hexagonal base) + 6×(Area of rectangular faces) = 6s(a + h).
Total surface area of the hexagonal prism (TSA) = 6s(a + h) sq. units.
Where “a” is the apothem length,
“s” is the length of the base edge, and
“h” is the height of the prism.
The formula to determine the surface area of a hexagonal prism in the case of a regular hexagonal prism, TSA = 6sh + 3√3s2.
Total surface area of the hexagonal prism (TSA) = 6sh + 3√3s2 sq. units.
Where “s” is the length of the base edge, and
“h” is the height of the prism.
Volume of a Hexagonal Prism
The volume of a hexagonal prism is the amount of space enclosed by it in three-dimensional space. It is also referred to as the amount of substance that it can hold, which is the capacity of a hexagonal prism. The formula for the volume of a hexagonal prism is equivalent to the product of its base area and height, which is measured in terms of cubic units such as cm3, m3, in3, etc.
The formula for finding the volume of a hexagonal prism is given as follows,
Volume of the Hexagonal Prism (V) = Base area × height
The formula for calculating the volume of a hexagonal prism when the length of the edge of the base and height of the prism is known is given as follows.
Volume of the Hexagonal Prism (V) = [(3√3)/2]s2h
Where “s” is the length of the base edge, and
“h” is the height of the prism.
The formula for calculating the volume of a hexagonal prism when the apothem length, length of the edge of the base, and height of the prism are known is given as follows.
Volume of the Hexagonal Prism (V) = 3ash
Where “a” is the apothem length,
“s” is the length of the base edge, and
“h” is the height of the prism.
Solved Example on Volume of a Hexagonal Prism
Example 1: Calculate the volume of a hexagonal prism with a base edge length of 15 cm and a height of 12 cm.
Solution:
Given data,
Length of the base edge (s) = 15 cm
The height of the prism (h) = 12 cm
We know that,
The volume of a hexagonal prism = [(3√3)/2]s2h
= (3/2) × (1.732) × (15)2 × 12
= 7,014.805 cu. cm
Hence, the volume of the hexagonal prism is 7,014.805 cu. cm.
Example 2: Determine the volume of the hexagonal prism if its height is 10 inches and its base area is given as 60 sq. in.
Solution:
Given data,
Base area = 60 sq. in
The height of the prism (h) = 10 inches
We know that
The volume of the hexagonal prism (V) = Base area × height
= 60 × 10 = 600 cu. in
Hence, the volume of the hexagonal prism is 600 cu. in.
Example 3: Calculate the volume of a hexagonal prism if its height is 13 cm, the length of each side of the base is 10 cm, and the apothem length is 8 cm.
Solution:
Given data,
Length of the base edge length (s) = 10 cm
Apothem length (a) = 8 cm
The height of the prism (h) = 13 cm
We know that
The volume of the hexagonal prism (V) = 3ash cubic units
= 3 × 8 × 10 × 13 = 3,120 cu. cm
Hence, the volume of the hexagonal prism is 3,120 cu. cm.
Example 4: Find the total surface area of a hexagonal prism if the length of each side of the base is 8 cm and the height is 10 cm.
Solution:
Given data,
Length of the base edge (s) = 8 cm
The height of the prism (h) = 10 cm
We know that,
The total surface area of the hexagonal prism = 6sh + 3√3s2
= 6 × 8 × 10 + 3√3 × (8)2
= 480 + 3√3 × 64
= 480 + 332.554 = 812.554 sq. cm
Thus, the total surface area of the hexagonal prism is 812.554 sq. cm.
Example 5: Determine the lateral surface area of a hexagonal prism with a base edge length of 12 cm and a height of 9 cm.
Solution:
Given data,
Length of the base edge length (s) = 12 cm
The height of the prism (h) = 9 cm
We know that,
The lateral surface area of a hexagonal prism = 6sh sq. units
LSA = 6 × 12 × 9
LSA = 648 sq. cm
Hence, the volume of the hexagonal prism is 648 sq. cm.
FAQs on Hexagonal Prism
Question 1: What is the Volume of a Hexagonal Prism?
Answer:
The volume of a hexagonal prism is the amount of space enclosed by it in three-dimensional space. It is also referred to as the amount of substance that it can hold, which is the capacity of a hexagonal prism. The formula for the volume of a hexagonal prism is equivalent to the product of its base area and height, which is measured in terms of cubic units such as cm3, m3, in3, etc.
The formula for finding the volume of a rectangular prism is given as follows,
The volume of the hexagonal prism (V) = Base area × height
Question 2: How to determine the Volume of a Hexagonal Prism?
Answer:
Follow the steps given below to determine the volume of a hexagonal prism:
Step 1: Calculate the base area of the prism using the appropriate formula.
Step 2: Note down the value of the height of the given hexagonal prism.
Step 3: Substitute the values of the given dimensions in the formula, V = [(3√3)/2]s2h
Step 4: Finally, write the final value in appropriate cubic units.
Question 3: How can we determine the Volume of a Hexagonal Prism when its Base Area and Height are given?
Answer:
We know that the general formula for calculating the volume of any prism is the product of its base area and its height. A hexagonal prism is a prism that has a hexagon as its base. So, we can also use the same formula for determining the volume of a hexagonal prism. As both the base area and the height of the hexagonal prism are given, the formula to determine the volume of a hexagonal prism is given as follows:
Volume of a hexagonal prism = Base Area × height.
Question 4: What will happen to the Volume of the Hexagonal Prism if its Height is reduced to Half?
Answer:
We know that the formula for calculating the volume of the hexagonal prism is V = 3abh. Where “a” is the apothem length, “s” is the length of the base edge, and “h” is the height of the prism. So, the volume of the prism is directly proportional to its height. So, if the height is reduced to half, the new height will become (h/2). So, the volume of the new hexagonal prism will be 3ab (h/2) = (1/2) (3abh) = V/2. Therefore, we can conclude the volume will also be reduced by half.
Question 5: What is meant by the Surface Area of a Hexagonal Prism?
Answer:
The total area that is covered by the surfaces of a hexagonal prism is referred to as its surface area. The surface area of a prism is measured in terms of square units such as sq. m, sq. cm, sq. in, etc. The formula to determine the surface area of a hexagonal prism is given as follows:
Total Surface Area, TSA = 2(Area of hexagon base) + 6(Area of rectangle faces) = 6s(a + h), where the “a” is apothem length of the prism, “s” is the length of the base edge, and “h” is the height of the prism.
The formula to determine the surface area of a hexagonal prism in the case of a regular hexagonal prism, TSA = 6sh + 3√3s2.
Question 6: How to determine the Lateral Surface Area of a Hexagonal Prism?
Answer:
Follow the steps mentioned below to determine the lateral surface area of the hexagonal prism:
- Step 1: Note down the values of the apothem length, base length, and height of the given hexagonal prism.
- Step 2: Substitute the given values in the formula of the lateral surface area of a hexagonal prism, LSA = 6sh.
- Step 3: Write the resulting value in square units.
Общие сведения
Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.
Кроме основания и граней, в состав стереофигуры входит:
- высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
- боковые рёбра — стороны, являющиеся общими для боковых граней;
- вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
- диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
- диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.
Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.
В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.
Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.
Свойства шестигранника
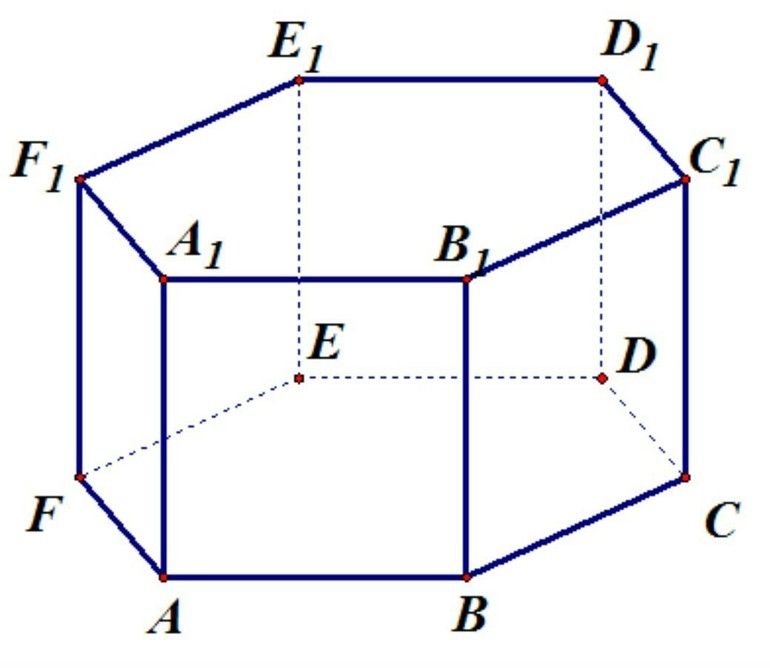
Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.
Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:
- Площадь основания. Так как в основе тела лежат правильные шестиугольники, то, используя их свойства, можно получить формулу: S = (3 * a 2 * √ 3) / 2, где: а — сторона многоугольника.
- Площадь полной поверхности. Определяется она из равенства: Sb = 6 * a * h + 2 * (3 * a 2 * √ 3) / 2. Из-за того, что площадь плоскости можно получить путём сложения сторон призмы и двух поверхностей её основания, а грань — прямоугольник (S прямоугольника = a * h), то указанная формула будет верной.
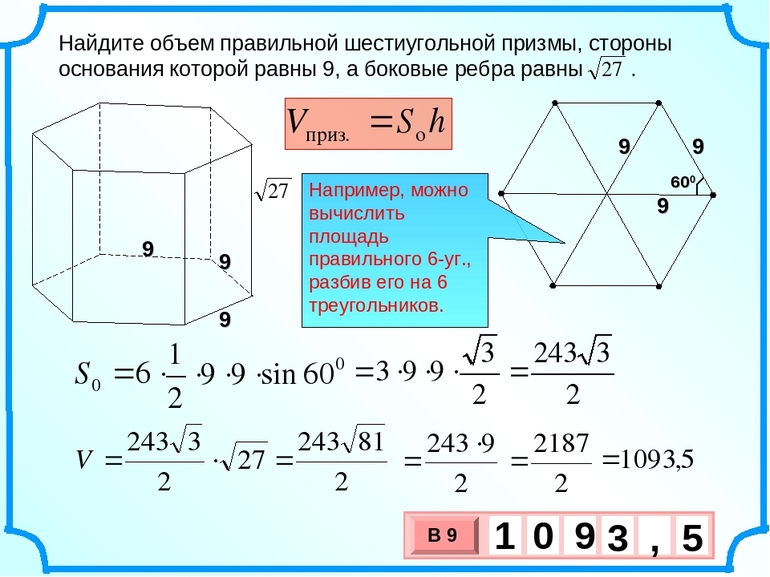
- Объём. Он равняется произведению площади основания на высоту. Роль последней может играть ребро любой стороны, например, BB1. Учитывая сказанное, формулу можно записать так: V = S * BB 1 = ((3 √ 3) / 2) * (a2 * h).
Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .
Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.
По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA12 + AE2)= √(h2 + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB12 + BE2) = √(h2 + 4 *a) = √5 *a. Сторона FE1 = √(FE2 + EE2) = √(h2 + a2) = √2 *a.
Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h2 + a2), что и следовало доказать.
Решение простого примера
Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.
Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.
Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.
Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.
С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.
Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E2 = C1C2 + CE = 22 + (4 c3) 2. C1E2 = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.
Задача высокого уровня
Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.
Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.
В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.
Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.
Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.
Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R2 = (12 * 2) / 3 √ 3 = 8 /√3.
Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a2 * sin60 / 2 = (R2 * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.