Как найти площадь половины шара

Сегмент шара

Сферический сегмент

Шаровым сегментом называется часть шара, отсеченная от него плоскостью.

Формулы:
$S_{lateral}=2 pi R H$ — площадь боковой поверхности
— площадь основания
$V=pi H^2(R- frac{1} {3} H)$ — формула объема

Сегмент шара

Точность вычисления

Знаков после запятой: 5

Площадь боковой поверхности

Слой шара

Сферический слой

Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.

Формулы:
$S_{lateral}=2 pi R (H_2-H_1)$ — площадь боковой поверхности
$V = pi left[ H_2^2 left( R - frac{1} {3} H_2 right) - H_1^2 left( R - frac{1} {3} H_1 right) right]$ — объем

Шаровой слой

Точность вычисления

Знаков после запятой: 5

Площадь боковой поверхности

Источник

The surface area of a hemisphere is the area covered by the faces of the hemisphere. The curved surface area and the base area sum up to make the total surface area of the hemisphere. The area of only the curved part is called the curved surface area of hemisphere. Before learning the formula for the surface area of hemisphere, let’s understand what is hemisphere followed by the formula and solved examples.

What is the Surface Area of a Hemisphere?

The surface area of a hemisphere is also known as the total surface area of hemisphere. The total surface area of a hemisphere is the total area of all the faces (curved and base area). A hemisphere is formed when a plane divides a sphere into two equal parts. To put it another way, a hemisphere is an exact half of a sphere in geometry. It is made up of two parts: hemi, which means half, and sphere, which is a 3D mathematical shape. When a sphere is sliced at the precise center along its diameter, two equal hemispheres are generated. As a result, a hemisphere is a three-dimensional geometric object consisting of half of a sphere with one side flat and the other as a round bowl.

Surface Area of a Hemisphere Formula

The surface area of a hemisphere is the total surface area of a hemisphere. The surface area of hemisphere is defined by two types of hemispheres, the solid hemisphere, and the hollow hemisphere. The surface area can be found in two ways:

The curved surface area of a hemisphere (CSA).
The total surface area of a hemisphere (TSA).

Curved Surface Area of Hemisphere Formula

The curved surface area of hemisphere formula is defined as the area covered by its curved surface. It is equal to half of the total surface area of a sphere. The formula for the curved surface area of hemisphere equals two times the product of pi and the square of the radius of the hemisphere.

Curved surface area of a hemisphere = 1/2 (Curved surface area of a sphere)

CSA = 1/2 (4πr²)

CSA = 2πr²

Therefore, the formula for curved surface area of hemisphere formula becomes,

CSA = 2πr²

Where,

CSA is the curved surface area,

π is a constant with the value of 3.14,

r is the radius of hemisphere.

Base Area

The base of the hemisphere is in a circular shape, and therefore, the formula for the base area of the hemisphere is equal to the area of a circle.

Base Area = πr²

Total Surface Area of a Hemisphere Formula

The total surface area of a hemisphere is defined as the total space covered by the surface of the hemisphere. The total surface area is given by the sum of its curved surface area and base area. The formula for total surface area equals three times the product of the pi (π) and the square of the radius of the hemisphere.

Total surface area of a hemisphere = Curved surface area + Base area

TSA = 2πr² + πr²

TSA = 3πr²

Therefore, the formula for the total surface area of a hemisphere becomes,

TSA = 3πr²

Where,

TSA is the total surface area,

π is a constant with the value of 3.14,

r is the radius of hemisphere.

Surface Area of a Hollow Hemisphere Formula

The surface area of a hollow hemisphere formula should be first explained in order to understand the formula well. A hollow hemisphere has two diameters as the hollow inner hemisphere creates another smaller diameter. If noted carefully, it can be seen that the surface area of a hollow hemisphere consists of the curved surface area of the bigger hemisphere, the curved surface area of the smaller hemisphere, and the area of the remaining base. Let’s break down the areas in order to obtain the surface area of a hollow hemisphere,

The curved surface area of the outer hemisphere = 2πR²
The curved surface area of the inner hemisphere = 2πr²
The base area of the hollow hemisphere = π(R² – r²)

Therefore, the total surface area of the hemisphere = 2πR² + 2πr²+ π(R² – r²)

TSA = 2πR² + 2πr² + πR² – πr²

TSA = 3πR² + πr²

How to Find the Surface Area of a Hemisphere?

The surface area of a hemisphere can be found by following easy steps based on what type of hemisphere is given. If a solid hemisphere is given, the formula of total surface area and curved surface area can be used based on the requirement, and if a hollow hemisphere is given, the formula for a hollow hemisphere must be used. Following are the steps that can be followed to obtain the surface areas based on the requirement.

Curved Surface Area of a Hemisphere

The formula for the curved surface area of a hemisphere when the given radius is “r” is 2πr². Below are the steps provided to find the curved surface area of a hemisphere:

Note down the radius of the hemisphere.
Put the “r” value in the formula for the curved surface area of sphere, that is, CSA = 2πr².
Present the final answer in square units.

Example: Calculate the curved surface area of a hemisphere radius of 5 m. (Use π = 3.14).

Solution:

We have,

r = 5

Using the formula we get,

CSA = 2πr²

= 3 (3.14) (5)²

= 235.5 sq. m

Total Surface Area of a Hemisphere

The formula for the total surface area of a hemisphere when the given radius is “r” is 3πr². Below are the steps provided to find the curved surface area of a hemisphere:

Note down the radius of the hemisphere.
Put the “r” value in the formula for the total surface area of sphere, that is, TSA = 3πr².
Present the final answer in square units.

Example: Calculate the total surface area of a hemisphere diameter of 16cm.

Solution:

We have,

d = 16cm

r = 8cm

Using the formula we get,

TSA = 3πr²

= 3 (3.14) (8)²

= 602.88 sq. cm.

Surface Area of a Hollow Hemisphere

The formula for the surface area of a hollow hemisphere when the given radius is “r” is 3πR²+ πr². Below are the steps provided to find the surface area of a hollow hemisphere:

Note down the radius of the hemisphere.
Put the “r” value in the formula for the total surface area of a sphere, that is, TSA = 3πR²+ πr².
Present the final answer in square units.

Real-Life Examples of Hemisphere

The examples of hemispheres can be seen in everyday life. For instance, the bowl that we use to eat food from is nothing but a hollow hemisphere. The half-cut shell of the coconut is an example of a hollow hemisphere. When we cut round-shaped fruits like oranges, tamarind, watermelon, etc., the shape of the fruit becomes a solid hemispherical shape. Below shown images are real-life examples of hemispheres.

Solved Example on Surface Area of Hemisphere

Example 1: Calculate the total surface area of a hemisphere radius of 4 m.

Solution:

We have,

r = 4

Using the formula we get,

TSA = 3πr²

= 3 (3.14) (4)²

= 150.72 sq. m

Example 2: Calculate the radius of a hemisphere if its total surface area is 200 sq. m.

Solution:

We have,

A = 200

Using the formula we get,

A = 3πr²

=> r² = A/3π

=> r² = 200/3 (3.14)

=> r = 4.60 m

Example 3: Calculate the radius of a hemisphere if its total surface area is 350 sq. m.

Solution:

We have,

A = 200

Using the formula we get,

A = 3πr²

=> r² = A/3π

=> r² = 350/3 (3.14)

=> r = 6.09 m

Example 4: Calculate the curved surface area of a hemisphere radius of 4 m.

Solution:

We have,

r = 4

Using the formula we get,

CSA = 2πr²

= 3 (3.14) (4)²

= 150.72 sq. m

Example 5: Calculate the radius of a hemisphere if its curved surface area is 790 sq. m.

Solution:

We have,

A = 790

Using the formula we get,

A = 2πr²

=> r² = A/2π

=> r² = 350/2 (3.14)

=> r = 7.46 m

FAQs on Surface Area of a Hemisphere

Question 1: What is the lateral surface area of a hemisphere?

Answer:

The lateral surface area of hemisphere is another name for the curved surface area of hemisphere and the formula for curved surface area of a hemisphere is 2πr².

Question 2: How to find the base area of a hemisphere?

Answer:

The base area of hemisphere has circular shape and therefore, the area of circle will be used to find the base area of hemisphere. Hence, base area becomes πr².

Question 3: How to find the surface area of a hemisphere?

Answer:

The formula for total surface area of a hemisphere when the given radius is “r” is 3πr². Below are the steps provided to find curved surface area of a hemisphere:

Note down the radius of the hemisphere.

Put the “r” value in the formula for total surface area of sphere, that is, TSA = 3πr².

Present the final answer in square units.

Question 4: Explain the difference between the curved surface area of hemisphere and the surface area of a hemisphere.

Answer:

The curved surface area of hemisphere is only the area covered by the curved surface and the formula for curved surface area of hemisphere is 2πr². While the surface area of a hemisphere is the sum of the curved surface area and the base area of hemisphere, therefore, the formula for TSA becomes 3πr².

Question 5: What is the surface area of a hemispherical shell?

Answer:

The surface area of a hemisphere shell is equal to the surface area of a solid hemisphere as we are looking at the surface of the hemisphere and not volume. Therefore, the surface area of the hemispherical shell is 3πr².

Surface Area of a Sphere

Surface Area of a Cube

Surface Area of a Cuboid

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.

Определение сегмента шара
Формулы для нахождения площади сегмента шара
- Площадь основания
- Площадь сферической поверхности
- Площадь полной поверхности
Пример задачи

Определение сегмента шара

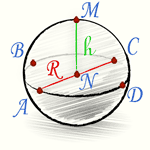
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.

R – радиус шара;
r – радиус основания сегмента;
h – высота сегмента; это длина перпендикуляра от центра его основания (точка O₂) до точки на поверхности шара.

Связь между радиусом основания сегмента, его высотой и радиусом шара:

Формулы для нахождения площади сегмента шара

Площадь основания

Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):

S_осн. = πr²

Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.

Площадь сферической поверхности

Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.

S_{сфер. пов.} = 2πRh

Площадь полной поверхности

Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.

S_полн. = S_осн. + S_{сфер. пов.} = π (2Rh + r²)

Пример задачи

Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.

Решение

Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.

S_осн. = 3,14 ⋅ (4,7 см)² = 69,3626 см²

S_{сфер. пов.} = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см²

S_полн. = S_осн. + S_{сфер. пов.} = 69,3626 см² + 90,432 см² = 159,7946 см²

Источник

У этого термина существуют и другие значения, см. сегмент.

Пример сферического сегмента (окрашен синим цветом). Вторая половина сферы также представляет собой сферический сегмент

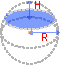
Сфери́ческий сегме́нт — поверхность, часть сферы, отсекаемая от неё некоторой плоскостью. Плоскость отсекает два сегмента: меньший сегмент называется также сферическим кругом^[1].
Если секущая плоскость проходит через центр сферы, то высота обоих сегментов равна радиусу сферы, и каждый из таких сферических сегментов называют полусферой.

Шарово́й сегме́нт — геометрическое тело, часть шара, отсекаемая от него некоторой плоскостью. Поверхностью шарового сегмента является объединение сферического сегмента и круга (основания шарового сегмента), границы которых совпадают.

Объём и площадь поверхности[править | править код]

Если радиус основания сегмента равен , высота сегмента равна , тогда объём шарового сегмента равен ^[2]

${displaystyle V={frac {pi h}{6}}(3a^{2}+h^{2}),}$

площадь поверхности сегмента равна

или

${displaystyle A=2pi r^{2}(1-cos theta ).}$

Параметры , и связаны соотношениями

${displaystyle r^{2}=(r-h)^{2}+a^{2}=r^{2}+h^{2}-2rh+a^{2},}$

${displaystyle r={frac {a^{2}+h^{2}}{2h}}.}$

Подстановка последнего выражения в первую формулу для вычисления площади приводит к равенству

${displaystyle A=2pi {frac {(a^{2}+h^{2})}{2h}}h=pi (a^{2}+h^{2}).}$

Заметим, что в верхней части сферы (синий сегмент на рисунке) ${displaystyle h=r-{sqrt {r^{2}-a^{2}}},}$ в нижней части сферы ${displaystyle h=r+{sqrt {r^{2}-a^{2}}},}$ следовательно, для обоих сегментов справедливо выражение и можно привести другое выражение для объёма:

${displaystyle V={frac {pi h^{2}}{3}}(3r-h).}$

Формула для определения объёма также может быть получена при интегрировании поверхности вращения:

${displaystyle V=int _{x}^{r}pi left(r^{2}-x^{2}right)dx=pi left({frac {2}{3}}r^{3}-r^{2}x+{frac {1}{3}}x^{3}right)={frac {pi }{3}}r^{3}(cos theta +2)(cos theta -1)^{2}.}$

Применение[править | править код]

Объём объединения и пересечения двух пересекающихся сфер[править | править код]

Объём объединения двух сфер радиусов r₁ и r₂ равен
^[3]

${displaystyle V=V^{(1)}-V^{(2)}}$

где

${displaystyle V^{(1)}={frac {4pi }{3}}r_{1}^{3}+{frac {4pi }{3}}r_{2}^{3}}$

является суммой объёмов двух сфер по отдельности, а

${displaystyle V^{(2)}={frac {pi h_{1}^{2}}{3}}(3r_{1}-h_{1})+{frac {pi h_{2}^{2}}{3}}(3r_{2}-h_{2})}$

является суммой объёмов двух сферических сегментов, образующих пересечение данных сфер. Пусть d < r₁ + r₂ — расстояние между центрами сфер, тогда исключение величин h₁ и h₂ приводит к выражению ^[4]^[5]

${displaystyle V^{(2)}={frac {pi }{12d}}(r_{1}+r_{2}-d)^{2}left(d^{2}+2d(r_{1}+r_{2})-3(r_{1}-r_{2})^{2}right).}$

Площадь поверхности, ограниченной кругами разных широт[править | править код]

Площадь поверхности, ограниченной кругами разных широт, является разностью площадей поверхности двух соответствующих сферических сегментов. Для сферы радиуса r и широт φ₁ и φ₂ данная площадь равна ^[6]

${displaystyle A=2pi r^{2}|sin varphi _{1}-sin varphi _{2}|.}$

Площадь квадратного участка поверхности шара[править | править код]

Участок, вырезанный на сфере радиуса r четырьмя дугами больших кругов, имеющими одинаковую угловую длину θ и попарно перпендикулярными (сферический квадрат, аналог квадрата на плоскости), имеет площадь

${displaystyle A=8r^{2}(1-cos theta /2).}$

Если угол θ мал (по сравнению с 1 радианом), то справедливо приближённое равенство, основывающееся на приближении ${displaystyle cos xto 1-x^{2}/2}$ при

${displaystyle Aapprox 8r^{2}{frac {theta ^{2}}{8}}=r^{2}theta ^{2}.}$

Например, площадь квадратного участка поверхности Земли (R_⊕ = 6378 км) со сторонами, равными 1 градусу, составляет

${displaystyle A(1^{circ })=8cdot R_{oplus }^{2}(1-cos 0{,}5^{circ })approx R_{oplus }^{2}cdot left({frac {pi }{180}}right)^{2}approx 12,391,{text{км}}^{2}.}$

1 квадратная секунда поверхности Земли имеет площадь в 3600² раз меньше: A(1′′) ≈ 12 391 км² / (60 · 60)² ≈ 956 м².

Обобщения[править | править код]

Сечения других тел[править | править код]

Сфероидальный сегмент получается при отсечении части сфероида таким образом, что она обладает круговой симметрией (обладает осью вращения). Аналогичным образом определяют эллипсоидальный сегмент.

Сегмент гиперсферы[править | править код]

Объём -мерного сегмента гиперсферы высотой и радиуса в -мерном евклидовом пространстве определяется по формуле ^[7]

${displaystyle V={frac {pi ^{frac {n-1}{2}},r^{n}}{,Gamma left({frac {n+1}{2}}right)}}int limits _{0}^{arccos left({frac {r-h}{r}}right)}sin ^{n}t,mathrm {d} t,}$

где Gamma (гамма-функция) задаётся выражением ${displaystyle Gamma (z)=int _{0}^{infty }t^{z-1}mathrm {e} ^{-t},mathrm {d} t.}$

Выражение для объёма можно переписать в терминах объёма единичного -мерного шара ${displaystyle C_{n}={pi ^{n/2}/Gamma left[1+{frac {n}{2}}right]}}$ и гипергеометрической функции ${displaystyle {}_{2}F_{1}}$ или регуляризованной неполной бета-функции ${displaystyle I_{x}(a,b)}$ как

${displaystyle V=C_{n},r^{n}left({frac {1}{2}},-,{frac {r-h}{r}},{frac {Gamma [1+{frac {n}{2}}]}{{sqrt {pi }},Gamma [{frac {n+1}{2}}]}}{,,}_{2}F_{1}left({tfrac {1}{2}},{tfrac {1-n}{2}};{tfrac {3}{2}};left({tfrac {r-h}{r}}right)^{2}right)right)={frac {1}{2}}C_{n},r^{n}I_{(2rh-h^{2})/r^{2}}left({frac {n+1}{2}},{frac {1}{2}}right).}$

Формула для площади поверхности может быть записана в терминах площади поверхности единичного -мерного шара ${displaystyle A_{n}={2pi ^{n/2}/Gamma left[{frac {n}{2}}right]}}$ как

${displaystyle A={frac {1}{2}}A_{n},r^{n-1}I_{(2rh-h^{2})/r^{2}}left({frac {n-1}{2}},{frac {1}{2}}right),}$

где

Также справедливы следующие формулы^[8]:
${displaystyle A=A_{n}p_{n-2}(q),quad V=V_{n}p_{n}(q),}$ где
${displaystyle q=1-h/r(0leq qleq 1),quad p_{n}(q)={frac {1-G_{n}(q)/G_{n}(1)}{2}},}$

${displaystyle G_{n}(q)=int limits _{0}^{q}(1-t^{2})^{(n-1)/2}dt.}$

При

${displaystyle G_{n}(q)=sum _{i=0}^{k}(-1)^{i}{binom {k}{i}}{frac {q^{2i+1}}{2i+1}}.}$

Было показано^[9], что при и ${displaystyle p_{n}(q)to 1-F({q{sqrt {n}}}),}$ где — стандартное нормальное распределение.

Литература[править | править код]

А. И. Маркушевич, А. Я. Хинчин, П. С. Александров. Основные понятия сферической геометрии // Энциклопедия элементарной математики. Книга 4 – Геометрия. — Москва: ГИФМЛ, 1963.

Примечания[править | править код]

Источник

Площадь поверхности шарового сегмента

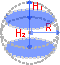
Часть шара, [шар, сфера] осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом. Основанием шарового сегмента называется круг ABCD. Высотой шарового сегмента называется отрезок NM, т.е. длина перпендикуляра, восстановленного из центра N основания до пересечения с поверхностью шара. Точка M называется вершиной шарового сегмента.

Площадь поверхности шарового сегмента равняется произведению его высоты на окружность большого круга шара.

[ S = 2 pi R h ]

(R – радиус большого круга шара, h=NM – высота шарового сегмента)

Формулы шара, сферы

Вычислить, найти площадь поверхности шарового сегмента по формуле (1)

Площадь поверхности шарового сегмента	стр. 318

Источник

Сегмент шара

Шаровой слой

What is the Surface Area of a Hemisphere?

Surface Area of a Hemisphere Formula

Curved Surface Area of Hemisphere Formula

Base Area

Total Surface Area of a Hemisphere Formula

Surface Area of a Hollow Hemisphere Formula

How to Find the Surface Area of a Hemisphere?

Curved Surface Area of a Hemisphere

Total Surface Area of a Hemisphere

Surface Area of a Hollow Hemisphere

Real-Life Examples of Hemisphere

Solved Example on Surface Area of Hemisphere

FAQs on Surface Area of a Hemisphere

Related Articles

Определение сегмента шара

Формулы для нахождения площади сегмента шара

Площадь основания

Площадь сферической поверхности

Площадь полной поверхности

Пример задачи

Объём и площадь поверхности[править | править код]

Применение[править | править код]

Объём объединения и пересечения двух пересекающихся сфер[править | править код]

Площадь поверхности, ограниченной кругами разных широт[править | править код]

Площадь квадратного участка поверхности шара[править | править код]

Обобщения[править | править код]

Сечения других тел[править | править код]

Сегмент гиперсферы[править | править код]

Литература[править | править код]

Примечания[править | править код]

Площадь поверхности шарового сегмента

Формулы шара, сферы

Вычислить, найти площадь поверхности шарового сегмента по формуле (1)

Площадь поверхности шарового сегмента

Добавить комментарий Отменить ответ

Сегмент шара

Шаровой слой

What is the Surface Area of a Hemisphere?

Surface Area of a Hemisphere Formula

Curved Surface Area of Hemisphere Formula

Base Area

Total Surface Area of a Hemisphere Formula

Surface Area of a Hollow Hemisphere Formula

How to Find the Surface Area of a Hemisphere?

Curved Surface Area of a Hemisphere

Total Surface Area of a Hemisphere

Surface Area of a Hollow Hemisphere

Real-Life Examples of Hemisphere

Solved Example on Surface Area of Hemisphere

FAQs on Surface Area of a Hemisphere

Related Articles

Определение сегмента шара

Формулы для нахождения площади сегмента шара

Площадь основания

Площадь сферической поверхности

Площадь полной поверхности

Пример задачи

Объём и площадь поверхности[править | править код]

Применение[править | править код]

Объём объединения и пересечения двух пересекающихся сфер[править | править код]

Площадь поверхности, ограниченной кругами разных широт[править | править код]

Площадь квадратного участка поверхности шара[править | править код]

Обобщения[править | править код]

Сечения других тел[править | править код]

Сегмент гиперсферы[править | править код]

Литература[править | править код]

Примечания[править | править код]

Площадь поверхности шарового сегмента

Формулы шара, сферы

Вычислить, найти площадь поверхности шарового сегмента по формуле (1)

Площадь поверхности шарового сегмента

Вам также может понравиться

Как найти таблицу символов в ворде

Как составить желание на здоровье

Как найти общий язык родителями мужа

Добавить комментарий Отменить ответ