Как найти площадь поля по формуле

Unit Converter

Enter the field length (ft) and the field width (ft) into the Field Area Calculator. The calculator will evaluate the Field Area. 

• All Area Calculators
• Reduction of Area Calculator
• Lawn Area Calculator
• House Area Calculator

Field Area Formula

The following two example problems outline the steps and information needed to calculate the Field Area.

FA = FL * FW

• Where FA is the Field Area (ft^2)
• FL is the field length (ft) 
• fW is the field width (ft) 

How to Calculate Field Area?

The following example problems outline how to calculate Field Area.

Example Problem #1:

1. First, determine the field length (ft). 
   • The field length (ft) is given as: 100.
2. Next, determine the field width (ft). 
   • The field width (ft) is provided as: 100.
3. Finally, calculate the Field Area using the equation above: 

FA = FL * FW

The values provided above are inserted into the equation below and computed.

FA = 100 * 100 = 10,000 (ft^2)

---

Example Problem #2: 

For this problem, the variables required are provided below:

field length (ft) = 200

field width (ft) = 200

Test your knowledge using the equation and check your answer with the calculator

.FA = FL * FW = ?

Что такое гектар земли

Для обозначения размеров земельных наделов используют разные значения площади. Сегодня мы расскажем, чему равен 1 гектар , что это такое и как перевести эту меру площади в другие значения.

Что такое гектар

Гектар — внесистемная единица измерения площади. Он равен площади квадрата со стороной 100 метров. 10 000 квадратных метров — это 1 гектар земли.

Гектары используют для обозначения площади больших участков, преимущественно сельскохозяйственного назначения. В настоящее время в России эта единица измерения площади введена в качестве внесистемной единицы без ограничения срока использования в областях применения «сельское и лесное хозяйство». МОЗМ — Международная организация законодательной метрологии — относит в своих рекомендациях гектар к единицам измерения, «которые могут временно применяться до даты, установленной национальными предписаниями, но которые не должны вводиться, если они не используются».

Интересный факт: впервые эта единица измерения и ее международное обозначение — ha — введены в 1879 году Международным комитетом мер и весов. Сегодня ha допущен к использованию вместе с другими единицами Международной системы единиц.

До введения гектара в России использовались другие меры площади. Например, для обозначения площади больших наделов использовали десятину — она примерно равна гектару. Также в обиходе применяли другие меры длины, например — версту. Она равна 1,6 километра. Сажень равнялся 2,13 метра, аршин — 0,71 метра, а одной из самых маленьких единиц измерения длины был вершок — он равнялся 0,045 метра или 4,5 сантиметра.

Какие еще меры площади существуют и когда их используют

Мы выяснили, сколько м² в 1 га — 10 тыс м². Помимо гектара, в России используют другие меры площади: квадратные километры, ары и квадратные метры. Более привычное и распространенное название аров — сотки. Каждая из принятых мер площади применяется в строго определенных ситуациях.

Квадратные километры — самая большая единица измерения площади, которая используется в России. Это — квадрат со стороной 1 000 м, в одном км² 1 000 000 м². Квадратные километры используют для определения площади городов, регионов, районов , отдельных континентов и даже планеты Земля. Например, общая площадь нашей планеты — 510 072 000 км². В одном квадратном километре 100 гектар. Соответственно, 1 ha — это всего лишь 0,01 от одного квадратного километра.

Гектары — вторая по величине единица измерения, которую используют в нашей стране. Чаще всего ее применяют для обозначения площади лесов, сельскохозяйственных угодий, полей для выращивания кормовых культур и других нежилых наделов. Площади больших земельных участков тоже могут выражаться в гектарах, но это происходит крайне редко — наделы, в которых больше 1 га, скорее являются исключением из правил.

Ары , или сотки — третья по величине единица измерения, самая распространенная в обиходе и известная всем. Сотка — это квадрат земли со стороной 10 м, в одной сотке — 100 квадратных метров. А 100 соток образуют площадь в один гектар. Ары используют для обозначения площади земельных участков — например, небольших наделов для личного сельскохозяйственного использования, участков в дачных поселках, небольших городах. Во всех объявлениях о продаже площадь наделов указывают в сотках.

Квадратные метры — еще одна распространенная мера площади. Ее используют преимущественно для обозначения площади дачных домов, частных жилых домов, коттеджей, комнат, квартир, таунхаусов и другой жилой недвижимости. В квадратных метрах измеряют и площадь коммерческих объектов — например, магазинов, складов, производственных цехов.

Как перевести в гектары квадратные метры и сотки

В 1 га (гектаре) 10 000 квадратных метров земли и 100 соток. Чтобы перевести одну меру площади в другую, нужно выполнить простые расчеты. Чтобы посчитать, сколько гектар в определенном количестве соток, нужно умножить число соток на 0,01, потому что один ар — это 0,01 часть гектара. Чтобы посчитать, сколько га в м², нужно умножить количество квадратных метров на 0,0001, потому что один квадратный метр — это 0,0001 часть ha.

Например: нам известны площади двух разных участков. Вы знаете, гектар — это сколько соток и м². Один участок — 23 сотки, другой участок — 350 квадратных метров. Обе площади нужно перевести в гектары. Для этого:

📌 умножаем 23 сотки на 0,01 — получаем 0,23, значит, в этом участке 0,23 гектара;

📌 умножаем 350 квадратных метра на 0,0001 — получаем 0,035, значит, в этом наделе 0,035 гектара.

Вы знаете, 1 га — сколько это в м² и сколько соток в одном гектаре . Чтобы произвести обратные расчеты — перевести площадь участка из гектар в сотки и квадратные метры, тоже нужно решить простой пример. В одном гектаре 100 соток, соответственно, чтобы перевести га в ары, нужно умножить площадь надела в гектарах на 100. В одном гектаре 10 тысяч м², значит, чтобы получить площадь надела в м², нужно умножить его площадь в га на 10 000.

Например. У нас есть три участка. Первый площадью 2 гектара, второй — 3,4 гектара, третий — 10,6 гектар. Нужно перевести эти площади в ары и квадратные метры, для этого:

📌 умножаем 2 на 100 и 10 000, получаем числа 200 и 20 000 — в наделе площадью 2 га 200 соток и 20 000 квадратных метров;

📌 умножаем 3,4 на 100 и 10 000, получаем 340 и 34 000 — в наделе площадью 3,4 га 340 соток и 34 000 квадратных метров;

📌 умножаем 10,6 на 100 и 10 000, получаем 1060 и 106 000 — в наделе площадью 10,6 га 1060 соток и 106 000 квадратных метров.

Для примера приведем простые расчеты:

✅ 100 соток — это 1 гектар;

✅ 2 гектара — это 20 000 в метрах в квадрате;

✅ 50 гектаров — это 500 000 в метрах в квадрате;

✅ 15 гектаров — это 150 000 в метрах в квадрате;

✅ 24 гектара — это 240 000 в метрах в квадрате.

Очевидно, что использовать общепринятые единицы измерения удобнее, чем переводить гектары в квадратные метры или сотки. Лучше обозначать площадь больших участков в квадратных километрах, средних — в гектарах, небольших — в сотках, совсем маленьких — в квадратных метрах. При необходимости можно легко перевести одну единицу измерения в другую с помощью калькулятора.

Как измерить площадь участка и какую единицу измерения использовать

Если вам нужно измерить площадь участка, можно использовать три способа замера.

👣 Пройти по участку . Этот способ не дает точных данных, потому что длина шагов у каждого разная. Подходит для вычисления площади небольшого участка — например, определенной зоны в огороде или плодовом саду.

Наметьте визуально квадрат или прямоугольник, площадь которого вы хотите узнать. Пройдите по одной его стороне, затем по другой — эти стороны должны соприкасаться в углу. Посчитайте количество шагов для каждой из сторон и приступите к расчетам.

Средняя длина шага взрослого человека — 70 сантиметров. Перемножьте число шагов одной стороны прямоугольника на 70 и разделите на сто — вы получите длину в метрах. Затем проведите те же расчеты, но используя количество шагов по другой стороне участка. Полученные два значения перемножьте между собой — у вас получится площадь участка, выраженная в квадратных метрах.

Например: вам нужно узнать площадь участка. Вы измерили его шагами и выяснили, что длина одной стороны — 56 шагов, а длина другой стороны — 78 шагов. Рассчитаем длину обеих сторон в метрах:

📌 56 × 70 / 100 = 39,2 метра;

📌 78 × 70 / 100 = 54,6 метра.

Перемножим полученные значения: 39,2 × 54,6. Получается 2140 квадратных метров — это площадь нашего участка. Если перевести ее в сотки, получится 21,4 сотки, а если в гектары — 0,214 гектар.

Этот способ практически не используют для выполнения расчета площади участков со сложной геометрией — например, трапециевидных.

📏 Использовать рулетку . Этот способ быстрее и точнее по сравнению с измерением шагами. Чтобы узнать площадь участка, просто измерьте его стороны рулеткой. Затем перемножьте полученные значения между собой — получите площадь в квадратных метрах.

Если нужно рассчитать площадь круглого участка или участка другой сложной формы, используйте специальные формулы для расчета. Например, чтобы найти площадь круглого участка, используйте формулу P=¼πd², где d — это диаметр, а π примерно равно 3,14.

👷 Заказать расчет у геодезистов. Этот способ замера требует денег — услуги геодезистов стоят денег. Зато он самый точный и не требует от вас временных затрат, расчетов. Геодезисты могут посчитать площадь участка сложной формы с точностью до сантиметра, а это важно, например, для межевания.

Онлайн калькулятор расчета площади земельного участка. Калькулятор расчета площади земельного участка по длине его четырех сторон. Введите длину сторон земельного участка и рассчитайте его площадь онлайн.

Калькулятор площади земельного участка

Простой способ рассчитать площадь земельного участка онлайн

Оставить Комментарий Отменить Комментарий

неправильно высчитывается площадь этим калькулятором. Меньше процента на 2.

• Аноним –> –>
• Ответить

Аноним –> –>

Ответить

Аноним –> –>

Ответить

Михаил –> –>

Ответить

зная только 4 стороны невозможно правильно определить площадьэто работает, только если участок примерно вписывается углами в окружностьчтобы правильно посчитать, нужно ещё два противолежащих угла знать. для этого нужны дирекционные углы из кадастрового плана

Если площадь участка рассчитывается по формуле Брахмагупты, подобной формуле Герона для треугольника, (а иначе по четырем сторонам площадь 4-угольника не просчитать), то она верна только для случая, когда суммы противоположных углов четырехугольника равны между собой и равна 180 градусов. То есть, когда фигуру можно вписать в окружность. В других случаях появится ошибка.

Инструкция для калькулятора расчета площади земельного участка неправильной формы

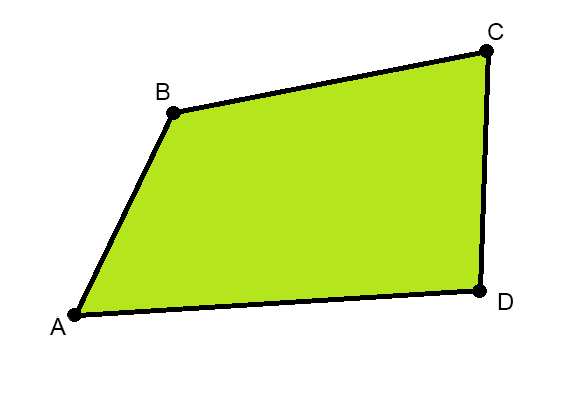
Примите к сведению, калькулятор Вариант 1 считает площадь участка, который вписывается углами в окружность. Проверить подходит ли Ваш участок под это условие можно, учитывая, что противоположные углы вписанного четырехугольника в сумме дают 180°. Если Ваш участок не вписывается в окружность, то калькулятор будет выдавать небольшую погрешность (величина который будет зависеть от того, насколько сильно Ваш участок не вписывается в окружность).

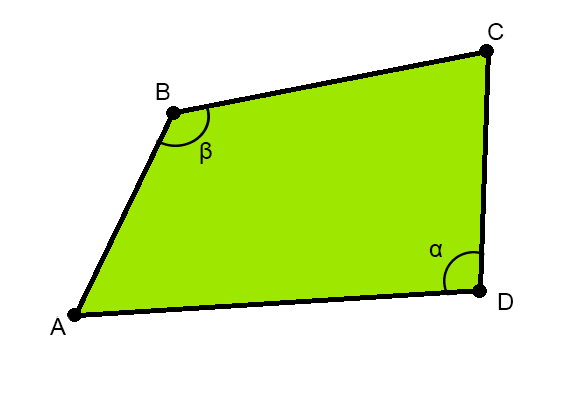
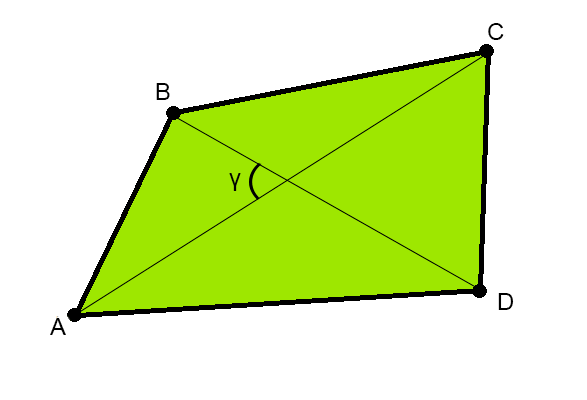
Впишите размеры сторон AB, BC, CD, DA в метрах.

Замеры участка проводят, с помощью длинной рулетки, лазерного дальномера, мерного колеса. Также можно изготовить деревянную треногу (наподобие циркуля) зафиксировав расстоянием между «ногами» в 1 м и, шагая таким приспособлением вдоль границы делянки подсчитать количество шагов.

Нажмите «Рассчитать».

Онлайн калькулятор позволяет определить площадь (в квадратных метрах, сотках, акрах и гектарах) земельного участка или поля, имеющего неправильную форму. Это пригодится для корректного оформления документов права собственности на землю, продажи, сдачи в аренду или его деления (т.н. межевания) без применения топографической съемки и специальных картографических программ. Также иногда просто нужно посчитать сколько соток имеет участок, чтобы прикинуть его рыночную стоимость.

2 467

1. Формула площади равнобедренной трапеции через стороны и угол

b – верхнее основание

a – нижнее основание

c – равные боковые стороны

α – угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R – радиус вписанной окружности

D – диаметр вписанной окружности

O – центр вписанной окружности

H – высота трапеции

α, β – углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d – диагональ трапеции

α, β – углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m – средняя линия трапеции

c – боковая сторона

α, β – углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b – верхнее основание

a – нижнее основание

h – высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам 

1. На клетчатой бумаге с размером клетки  изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: 

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

 , где и — диагонали.

Получим: 

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки  

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача.  Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 – 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга 

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в  раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в  раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.

Ответ: 7.

Задачи на координатной плоскости 

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.