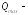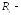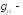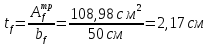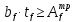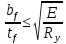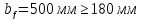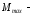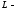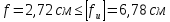Площадь – поперечное сечение – балка
Cтраница 1
Площадь поперечного сечения балки равна FI 2 ( 0 012 – 0 85 0 01 х х 1 68) 0 054 м2, т.е. почти на 43 % больше, чем у спроектированной балки. В соответствии с [7] примем, что вес продольных и поперечных ребер жесткости составляет 0 3 от веса несущих элементов.
[1]
Итак, площадь поперечного сечения балки при расположении ребра в сжатой зоне составляет 59 3 % от площади поперечного сечения балки при расположении ребра в растянутой зоне. При других соотношениях размеров тавра и других соотношениях допускаемых напряжений при растяжении и сжатии экономия будет иной.
[2]
F – площадь поперечного сечения балки; а Т / – – скорость распространения упругой деформации.
[3]
Отношение между площадью поперечного сечения балки и общей площадью нагреваемой поверхности оказывает влияние на прогреваемость бетона. Поэтому лучше применять балки широкие, а не тонкие и высокие. В качестве основной арматуры рекомендуется использовать более двух арматурных стержней и еще лучше разместить часть основной арматуры во втором ряду. Если балка во время пожара не имеет возможности свободно удлиняться из-за отсутствия температурных швов на концевых опорах или они недостаточны, то в балке будут возникать продольные сжимающие усилия, которые в общем повышают предел огнестойкости балки, но могут оказать и вредное влияние на опорные стены или колонны, вызывая у них изгиб. Вследствие воздействия огня на внутренних опорах неразрезных балок и плит при их пределе огнестойкости 1 5 ч и более возрастают поперечные силы и при отношении 2 5 / M / Q / io 3 снижается предел огнестойкости изгибаемого элемента.
[4]
J – момент инерции площади поперечного сечения балки относительно горизонтальной линии, проходящей через центр тяжести площади поперечного сечения; R – радиус кривизны оси изогнутой балки, который выражается формулой ( § 6 гл.
[5]
Сочетание требований равнопрочности и минимальности площади поперечного сечения балки ( последнее эквивалентно минимальности объема статически определимой балки) рассмотрено в статье А. Ю. Ишлинского О равнопрочном сечении балки ( Ученые записки Московского государственного университета, вып.
[6]
Этот интеграл представляет собой статический момент площади поперечного сечения балки относительно нейтральной оси. Он равен нулю, и, следовательно, нейтральная ось при изгибе проходит через центр тяжести сечения.
[7]
Этот интеграл представляет собой статический момент площади поперечного сечения балки относительно нейтральной оси. Он равен нулю, и, следовательно, нейтральная ось при изгибе проходит через центр тяжести сечения.
[8]
При этом величина, FI будет равна площади всего поперечного сечения балки. Если балка сначала собирается на прихватках, а затем свариваются швы / и 2, то изгиб от швов находится при эксцентр иси-тетах е3 и е2 ( рис. 6 – 15, а) и моменте инерции всего сечения. Расстояния е2 и е3 взяты от центра тяжести площади поперечного сечения балки до Центра тяжести площади пластических деформаций.
[9]
Здесь F, Sx, Sy, Ix, Iy, Ixy – площадь поперечного сечения балки, статические моменты этой площади относительно осей хну, осевые моменты инерции указанной площади относительно осей х и у и центробежный момент инерции площади в системе осей ху.
[10]
При определении продольного сокращения по формуле ( 22) в нее следует подставить площадь всего поперечного сечения балки F. Если балка сначала собрана на прихватках, а затем сваривают швы 1 н 2, то изгиб от швов находят при эксцентрицитетах РЗ и е2 ( рис. 19, а) и моменте инерции всего сечения двутавра.
[12]
А – юонстанта; Е – модуль Юнга; I – момент инерции площади поперечного сечения балки; р – масса единица длины; L – длина балки.
[13]
Итак, площадь поперечного сечения балки при расположении ребра в сжатой зоне составляет 59 3 % от площади поперечного сечения балки при расположении ребра в растянутой зоне. При других соотношениях размеров тавра и других соотношениях допускаемых напряжений при растяжении и сжатии экономия будет иной.
[14]
Как видно из формулы (7.52), несущая способность балки пропорциональна моменту сопротивления WKM, а расход материала – площади F поперечного сечения балки. Поэтому рациональными с точки зрения расхода материала являются такие типы сечений, у которых отношение WJF имеет возможно большее значение.
[15]
Страницы:
1
2
3
I-Beams are one of the several standard structural shapes for steel. These types of beams are often used in trusses in buildings. I beam is generally manufactured from structural steels with hot and cold rolling or welding processes. Due to its shape, I beam has the high moment of inertia and stiffness which makes it resistant to bending moments. The following Steel I beam cross-sectional area calculator has been developed to calculate the cross sectional area of structural steel I beams.
I-Beams are one of the several standard structural shapes for steel. These types of beams are often used in trusses in buildings. I beam is generally manufactured from structural steels with hot and cold rolling or welding processes. Due to its shape, I beam has the high moment of inertia and stiffness which makes it resistant to bending moments. The following Steel I beam cross-sectional area calculator has been developed to calculate the cross sectional area of structural steel I beams.
Code to add this calci to your website 
Formula:
A = 2Bh + Hb
Where,
A = Cross Section Area
B = Width
h = Flange Thickness
H = Flange-Flange Inner Face Height
b = Web Thickness
Example:
Calculate the Steel I Beam Cross-Sectional Area with the width of 50 mm, the flange thickness of 20 mm, flange-flange inner face height of 30 mm, and web thickness of 15 mm.
Solution:
Cross Section Area = (2 x 50 x 20) + (30 x 15)
= 2450 mm2.
В
курсовой работе следует запроектировать
главную балку среднего ряда, на которую
с двух сторон опираются вспомогательные
балки. Расчетная схема представляет
собой однопролетную шарнирно опертую
балку, нагруженную сосредоточенными
силами Р,
численно равными опорным реакциям двух
вспомогательных балок

Сосредоточенная
нагрузка от пары вспомогательных балок,
опирающихся на главную балку:
-
расчетная
эксплуатационная
-
расчетная
предельная
|
где, |
|
расчетная |
|
|
расчетная |
|
|
|
расчетная |
|
|
|
расчетная |
Нагрузка
на погонный метр участка шириной l:
-
расчетная
эксплуатационная
-
расчетная
предельная
Способ
определения изгибающих моментов и
поперечных сил зависит от количества
сил Р = 10, нагружающих балку. Если
количество сил Р ≥ 5, то нагрузка на
главную балку может быть принята как
равномерно распределенная на единицу
длины.
Определение усилий в главной балке
Определяем
опорные реакции:
Определяем
изгибающие моменты:
Момент
на опоре равен нулю.

поперечные усилия:
где,

– эмпирический коэффициент, учитывающий
нагрузку от собственного веса главных
балок
Рис.
3.1
Расчетная схема, эпюры изгибающих
моментов и поперечных сил главной балки
3.2 Подбор сечения главной балки
В
виду того, что главные балки имеют
значительные пролеты и воспринимают
большие нагрузки, их, как правило,
выполняют составными в виде двутавров,
сваренных из трех листов.
Сечение
составной сварной двутавровой балки
показано на рис. 3.2.
Для
проектирования этого сечения необходимо
определить четыре размера: hw
высоту стенки, tw
толщину стенки, bf
ширину полки, tf
толщину полки.
Определяем
требуемый момент сопротивления сечения
главной балки:
где,

расчетный изгибающий момент по длине
главной балки, кН⋅см;

для отношения Af
/ Aw = 0,5;

1,12
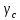
условий работы;

сопротивление стали, кН/см2.
Рис.
3.2. Схема поперечного сечения главной
балки
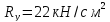
сопротивление стали главной балки.
Определяем
оптимальную высоту стенки исходя из
требований минимального расхода стали:
Окончательно
высота стенки увязывается с сортаментом
листовой прокатной стали.
Принимаем
высоту стенки hw
= 1500
мм.
|
В |
Выполняем
проверку прочности полученной толщины
стенки, исходя из ее работы на срез от
действия максимальной поперечной силы:
|
где, |
|
максимальная |
|
|
принятая |
|
|
|
расчетное |
|
|
|
характеристическое |
|
|
|
коэффициент |
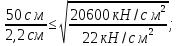
Принимаем
толщину стенки tw
= 14 мм.
Определяем
требуемую площадь поперечного сечения
одного пояса балки:
Производим
компоновку размеров поясного листа bf
и tf.
Ширину
поясного листа bf
принимаем в пределах:
Определяем
требуемую толщину пояса:
|
|
Окончательные
размеры bf
и tf
должны соответствовать стандартам
проката универсальной широкополочной
стали.
Принимаем
толщину пояса tf
=22 мм, ширину
пояса bf
= 500
мм.
Проверяем
выполнение требований:
-
-
условие
технологии свариваемости
-
условие
местной устойчивости сжатого пояса
-
условие
равномерного распределения напряжений
по ширине пояса
-
конструктивное
требование
-
конструктивное
требование
-
конструктивное
требование
Определяем
геометрические характеристики балки:
Момент
инерции:
Момент
сопротивления:
Статический
момент полки балки относительно
нейтральной оси:
Статический
момент полусечения относительно
нейтральной оси:
Принятое
сечение главной балки проверяется по
первой группе предельных состояний.
(3.20)
Определяем
площадь поперечного сечения стенки
балки:
Определяем
площадь поперечного сечения одного
пояса балки:
Расчетное
сопротивление стали сдвигу:

Определяем
нормальные напряжения:

где,

расчетный изгибающий момент относительно
оси х-х в сечении главной балки, кН∙см;

значение которого принимается в
зависимости от отношения Af
/ Aw;

сопротивления сечения нетто относительно
оси х-х, см3;

сопротивление стали главной балки,
кН/см2.
Коэффициент
определяется
в зависимости от отношения Af
/ Aw = 110


При
коэффициент β
=
Прочность
стенки на срез при действии максимальных
касательных напряжений проверяется в
соответствии с найденными фактическими
характеристиками сечения балки:

Для
обеспечения требований второй
группы предельных состояний
выполняется проверка деформативности
балки: фактический прогиб, не должен
превышать граничное значение, определенное
строительными нормами.
При
принятой расчетной схеме главной балки
фактический прогиб определяем по
формуле:
|
где, |
|
граничное |
|
|
максимальный |
|
|
|
пролет |
|
|
|
модуль |
|
|
|
момент |
|
|
|
расчетная |
|
|
|
расчетная |
Условие
выполняется, следовательно, сечение
подобрано удовлетворительно.
Соседние файлы в папке Металлы Новак
- #
10.02.201692.11 Кб11Дополнительное.dwg
- #
10.02.2016345.69 Кб7Лист на печать.bak
- #
10.02.2016478.01 Кб11Лист на печать.dwg
- #
10.02.2016684.02 Кб7Металич.констр.bak
- #
10.02.2016555.95 Кб13Металич.констр.dwg
- #
При строительстве деревянных домов, каркасных построек, деревянных надстроек над капитальными зданиями (мансарда, второй этаж) применяются почти всегда только деревянные балки перекрытий. Это связано как с необходимостью максимально близких физико-технических характеристик всех строительных материалов, так и с соображениями прочности – нет смысла на относительно легкие деревянные или каркасные стены монтировать тяжелые элементы перекрытий.
В современном строительстве используются деревянные балки трех видов:
- цельное или тесаное бревно – сравнительно редко, в основном при создании бревенчатых домов;
- цельный или срощенный брус – наиболее частый вариант, используется обычно именно цельный брус;
- клееные балки с сечением в виде прямоугольника, уголка, тавра или двутавра.
Соответственно, при расчете нагрузочной способности перекрытий, шага балок перекрытия и их сечения необходимо учитывать особенности выбранного материала и знать его характеристики.
Технические условия для деревянных балок перекрытия изложены в ГОСТ 4981-87. Этот документ предусматривает несколько видов балок:
- БЦ0 – балка из цельной древесины без черепных брусков;
- БЦ1 – то же, с одним черепным бруском;
- БЦ2 – то же с двумя черепными брусками;
- БК0 – балка из клееной древесины без черепных брусков;
- БК1 – то же, с одним черепным бруском;
- БК2 – то же с двумя черепными брусками.
Обратите внимание, что ГОСТ рассматривает балки из бруса с прямоугольным сечением, бревно-кругляк рассчитывается по отдельным нормативам.
По иллюстрациям хорошо видно – фактически ГОСТ рассматривает только балки с прямоугольным сечением, уголок и тавр, двутавр в документе не упоминается. Соответственно, и данные о размерах таких изделий, точнее, требования к размерам есть только для этих типов изделий (таблица 1).
Прочностные характеристики для расчетов берутся из СНиП II-25-80 для изделий из цельной древесины, ГОСТ 19414-90 для срощенного бруса и ГОСТ 20850-84 для клееного бруса.
Обычно принимают следующие расчетные сопротивления для древесины сортов 1…3 по таблице 2.
Если вместо хвойной древесины (сосна, ель) используются другие породы дерева, принимают данные из таблицы 3.
Площадь сечения, моменты инерции и сопротивления определяются по формулам из таблицы ниже (для квадратного и прямоугольного бруса).
Есть также уже готовый набор значений для типовых размеров бруса с квадратным сечением.
Таким образом, подставляя в стандартные расчетные формулы данные из таблиц 1…5, можно получить необходимые данные для деревянных балок с прямоугольным или квадратным профилем. Для более сложных сечений расчет вести сложнее, и если для балок типов БЦ и БК данные в ГОСТах есть, то для деревянного двутавра исходную информацию найти трудно – как минимум потому, что каждый производитель изготавливает двутавровые балки по собственным техническим условиям.
Фактически для расчета балки сложного сечения необходимо принимать формулы для вычисления момента инерции и сопротивления по таблице 7.
Полученные из таблиц данные используют для расчета прогиба балки (момент инерции) и для расчета несущей способности (момент сопротивления).
Таким образом, на основании приведенных данных и формул можно определить необходимую площадь сечения балки с простым или сложным профилем, а также ее прогиб. Если выбранное сечение удовлетворяет условиям прочности и обеспечивает прогиб менее допустимой величины, балка полностью подходит для строительства.





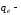
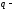
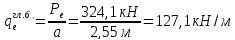







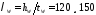 назначаем ее толщину:
назначаем ее толщину: