
Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.
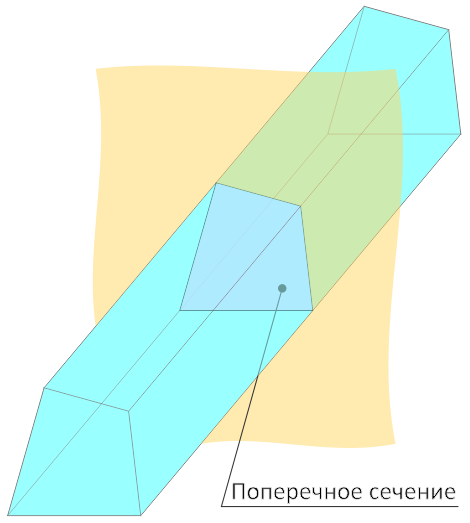
Сечение может иметь простую или сложную форму, а также быть составным.
Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.
Площадь поперечного сечения
В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.
Формулы для расчета площади основных фигур.
Пример:
Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением.

Для расчета общей площади, сложное сечение раскладывается на простые фигуры:
Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто.

В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:
A=A1+A2+A3-A4
Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.
Площадь составного сечения
Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым.

Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.
Эти сечения сами по себе тоже являются сложными.
Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.
В результате сложив все составляющие профили, получим площадь всего сечения.
Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.
Длина поперечного сечения
Длиной поперечного сечения называют полную (габаритную) длину фигуры как расстояние по горизонтали между двумя её наиболее удаленными точками.
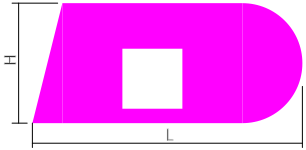
Длина поперечного сечения обозначается латинской буквой L или l и измеряется стандартно в миллиметрах или сантиметрах.
Ширина сечения определяется аналогично, но обозначается буквой H или h.
При решении задач, длину, ширину и площади поперечного сечения рекомендуется переводить соответственно в метры и м2.
Понятие «поперечное сечение» является одним из основных при расчетах на прочность в сопротивлении материалов и технической механике.
Различают два основных вида расчета площади сечений:
- Геометрический — когда требуется найти площадь сечения тела по известным размерам;
- Прочностной — расчет площади поперечного сечения бруса проводится по условию прочности.
Пример расчета поперечных сечений >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:

Понятие о геометрических характеристиках однородных поперечных сечений. Центр тяжести; статические моменты; моменты инерции – осевые, центробежный, полярный; моменты сопротивления; радиусы инерции. Главные оси и главные моменты инерции. Понятие об упруго-геометрических характеристиках неоднородных сечений.
2. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ
2.1. Некоторые сведения о геометрических характеристиках
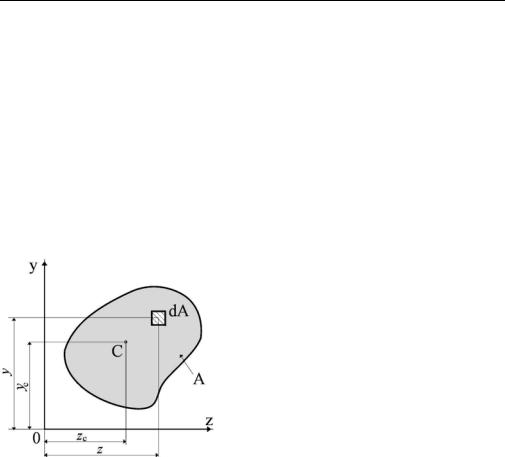
Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации).
Рассмотрим произвольное поперечное сечение A (сечение бруса) с координатами центра тяжести zc, yc. В точке (z, y) выделим элемент площади dA. Основные геометрические характеристики поперечных сечений элементов конструкций (в том числе и данного сечения) описываются интегралами следующего вида
∫ym zn dA.
A
Рассмотрим некоторые характерные варианты записи этого интеграла и получим выражения для основных геометрических характеристик.
Площадь поперечного сечения
При m=0, n=0 интеграл приобретает вид
∫dA = A ,
A
а соответствующая характеристика, как видим, представляет собой площадь поперечного сечения элемента.
Оказывается, что во многих случаях деформирования тела знание только площади его поперечного сечения недостаточно.
Статические моменты
Если m=1, n=0, тогда получим характеристику
∫y dA = Sz ,
A
которая называется статическим моментом относительно оси z,
или, при m=0, n=1,
∫z dA = Sy
A
статическим моментом относительно оси y.
12
Статический момент относительно данной оси – сумма произведений элементарных площадей dA на их расстояние до данной оси, взятая по всей площади сечения А.
На основании теоремы Вариньяна (из курса теоретической механики) следует, что
|
Sz = ∫y dA =yc A, |
Sy = ∫z dA =zc A, |
|
A |
A |
а для сложного сечения (состоящего из нескольких простых, каждое из кото-
|
рых имеет площадь Ai и координаты собственного центра тяжести yc |
, zс ) |
|
|
i |
i |
|
|
Sz = ∑yci Ai , |
Sy = ∑zci Ai . |
Статический момент относительно какой-либо оси равен произведению всей площади фигуры на расстояние от ее центра тяжести до этой оси.
Отсюда можем получить формулы для определения координат центра тяжести сечения:
|
y = |
Sz |
= ∑yci Ai , |
z |
= |
Sy |
= ∑zci Ai . |
|
c |
A |
∑Ai |
c |
A |
∑Ai |
|
Как видим, относительно осей, проходящих через центр тяжести сечения, статические моменты равны нулю, а сами эти оси называются центральными.
Размерность статических моментов – м3 в системе СИ.
Осевые моменты инерции
Если m=2, n=0, тогда получим характеристику
∫y2 dA = Jz ,
A
которая называется осевым моментом инерции относительно оси z,
или, при m=0, n=2,
∫z2 dA = J y –
A
осевым моментом инерции относительно оси y.
Осевой момент инерции относительно данной оси – сумма произведений элементарных площадей dA на квадрат их расстояний до данной оси, взятая по всей площади сечения А.
Центробежный момент инерции
Если m=1, n=1, тогда получим характеристику
∫z y dA = Jzy ,
A
которая называется центробежным моментом инерции.
13

Центробежный момент инерции относительно осей координат – сумма произведений элементарных площадей dA на их расстояния до этих осей, взятая по всей площади сечения А.
Если хотя бы одна из осей y или z является осью симметрии сечения, центробежный момент инерции такого сечения относительно этих осей равен нулю (так как в этом случае каждой положительной величине z·y·dA можем поставить в соответствие точно такую же, но отрицательную, по другую сторону от оси симметрии сечения, см. рисунок).
Рассмотрим дополнительные геометрические характеристики, которые могут быть получены из перечисленных основных и также часто используются в расчетах на прочность и жесткость.
Полярный момент инерции
Полярным моментом инерции Jp называют характеристику
J p = Jz + J y .
С другой стороны,
J p = Jz + J y = ∫y2 dA +∫z2 dA = ∫(y2 + z2 ) dA = ∫ρ2 dA.
A A A A
Полярный момент инерции (относительно данной точки) – сумма произведений элементарных площадей dA на квадраты их расстояний (ρ2 = y2 + z2 ) до этой точки, взятая по всей площади сечения А.
Размерность моментов инерции – м4 в СИ.
Момент сопротивления Момент сопротивления относительно некоторой оси – величина равная мо-
менту инерции относительно той же оси отнесенному к расстоянию (ymax или zmax) до наиболее удаленной от этой оси точки
|
W = |
J |
z |
; W |
= |
J y |
. |
|
z |
ymax |
y |
zmax |
|||
Размерность моментов сопротивления – м3 в СИ.
Радиус инерции Радиусом инерции сечения относительно некоторой оси, называется величи-
на, определяемая из соотношения:
|
iz = |
J |
z |
, |
iy = |
J y |
. |
|
|
A |
A |
||||||
Радиусы инерции выражаются в м в системе СИ.
Замечание: сечения элементов современных конструкций часто представляют собой некоторую композицию из материалов с разным сопротивлением упругим деформациям, характеризуемым, как известно из курса физики, модулем Юнга E. В самом общем случае неоднородного сечения модуль Юнга является непрерывной функцией координат точек сечения, т. е. E=E(z, y). Поэтому жесткость неоднородного по упругим свойствам сечения
14
характеризуется более сложными, чем геометрические характеристики однородного сечения, характеристиками, а именно упруго-геометрическими вида
∫E (z, y) ym zn dA.
A
2.2. Вычисление геометрических характеристик простых фигур
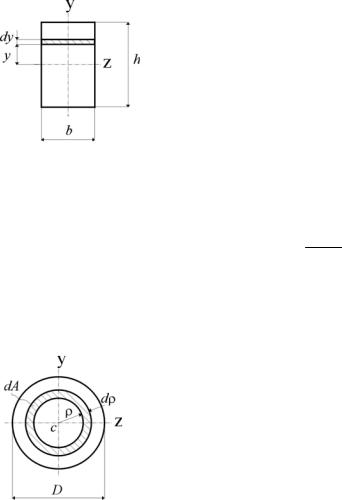
Прямоугольное сечение
Определим осевой момент инерции прямоугольника относительно оси z.
Разобьем площадь прямоугольника на элементарные площадки с размерами b (ширина) и dy (высота). Тогда площадь такого элементарного прямоугольника (заштрихован) равна dA=b·dy. Подставляя значение dA в первую формулу, получим
|
Jz = ∫y2 dA = +h∫/ 2 y2 b dy =b |
y3 |
+h / 2 = |
b h3 |
. |
||
|
3 |
12 |
|||||
|
A |
−h / 2 |
−h / 2 |
||||
По аналогии запишем
J y = h12b3 .
Подобным образом можно получить геометрические характеристики и для других простых фигур.
Круглое сечение
Сначала удобно найти полярный момент инерции Jp.
Затем, учитывая, что для круга Jz=Jy, а Jp=Jz+Jy, найдем
Jz=Jy=Jp/2.
Разобьем круг на бесконечно малые кольца толщиной dρ и радиусом ρ; площадь такого кольца dA = 2 π ρ dρ. Подставляя выражение для dA в выражение для Jp и интегрируя,
получим
|
J p = ∫ρ2 dA = D∫/ 2 ρ2 2 π ρ dρ= 2 π |
ρ4 |
D / 2 = |
π D4 |
, |
||||||
|
A |
0 |
4 |
0 |
32 |
||||||
тогда |
J p |
π D4 |
||||||||
|
Jz = J y = |
= |
. |
||||||||
|
2 |
64 |
|||||||||
2.3. Вычисление моментов инерции относительно параллельных осей
Пусть известны моменты инерции произвольного сечения относительно центральных осей z и y:
|
Jz = ∫y2 dA ; |
J y = ∫z2 dA; |
Jzy = ∫z y dA. |
|
A |
A |
A |
15
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нормальные напряжения в поперечных сечениях бруса вычисляются по формуле [c.6]
А – площадь поперечного сечения бруса. — [c.6]
Чему равны нормальные напряжения в поперечных сечениях бруса ппи растяжении-сжатии [c.13]
Jр — полярный момент инерции поперечного сечения бруса k , — эффективный коэффициент концентрации напряжений при симметричном цикле изменения соответственно нормальных и касательных напряжений [c.5]
Mj , Му — изгибающий момент в поперечном сечении бруса соответственно относительно оси х или у, [c.6]
М , Мк — крутящий момент в поперечном сечении бруса [c.6]
Плоские поперечные сечения бруса остаются плоскими и поворачиваются на некоторый угол одно относительно другого. [c.154]
Цилиндрический брус, закрепленный одним концом и нагруженный парой сил с моментом М, действующей в плоскости поперечного сечения бруса, подвергается деформации, называемой кручением. Для изучения этого вида деформации на поверхность круглого резинового стержня наносят сетку из равноотстоящих окружностей и образующих (рис 131, а). Если один конец стержня закрепить, а другой нагрузить парой сил, действующей в плоскости, перпендикулярной к оси стержня, то можно заметить, что образующие цилиндра превращаются в винтовые линии большого шага (рис. 131, б), а прямоугольники сетки превращаются в параллелограммы. [c.187]
В отличие от простых видов деформации на практике нередки случаи, когда в поперечных сечениях бруса возникают сразу несколько внутренних силовых факторов. Такие случаи принято называть сложным сопротивлением. Расчеты на прочность и жесткость при сложном сопротивлении основываются обычно на принципе независимости действия сил. Необходимо заметить, что иногда указанные виды расчетов можно упростить, если пренебречь (в пределах требуемой степени точности) второстепенными деформациями и привести, таким образом, сложную деформацию к более простой. [c.195]
Наиболее удобным способом решения задач на косой изгиб является приведение его к двум прямым плоским изгибам Для этого возникающий в поперечном сечении изгибающий момент раскладывают на два изгибающих момента, которые действуют в плоскостях, проходящих через главные оси инерции сечения. При косом изгибе в поперечных сечениях бруса возникают в общем случае как поперечные силы, так и изгибающие моменты. Однако влиянием касательных напряжений, появление которых обусловлено действием сил Q, в расчетах на прочность обычно пренебрегают. [c.199]
Применив метод сечений, найдем, что в любом поперечном сечении бруса действуют изгибающие моменты Мр = = Рур и Мр = Р2р, а также продольная сила N = Р (рис. 140, б). Нетрудно заметить, что здесь, как и в рассмотренном выше случае, имеет место совместное действие косого изгиба с осевым растяжением (сжатием). А потому формула для определения напряжения в произвольной точке сечения с координатами 2 и у будет аналогична (12.19), т. е. [c.204]
Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную с координатными осями Ог и Оу (рис. 9). Выделим элемент площади dp с координатами 2, у. По аналогии с выражением для момента силы относительно какой-либо оси можно составить выражение и для момен- та площади, которое называется статическим моментом. Так, произведение элемента площади dF на расстояние у от оси Ог [c.13]
При поперечном изгибе, когда в сечениях бруса действует Q и М, возникают не только нормальные напряжения а, но и касательные напряжения т. [c.247]
При сложном изгибе в поперечных сечениях бруса в общем случае возникают четыре внутренних силовых фактора Q , Qy, [c.332]
Если опасное сечение известно, то в нем нужно отыскать опасные точки. Наглядное представление о распределении напряжений о (М ) и а (Mj) по поперечному сечению бруса дают соответствующие эпюры, представленные на рис. 322, б. Для построения эпюры суммарных напряжений а . необходимо провести базис эпюры перпендикулярно к нейтральной линии. Так как из формулы (12.1) следует, что эпюра а линейна, то для ее построения кроме известной нулевой точки достаточно вычислить какую-либо одну ординату, например для точки А. Очевидно наиболее напряженными точками сечения будут точки, наиболее удаленные от нейтральной линии — точки Д и В (рис. 322, б). В данном случае в точке А действует наибольшее растягивающее, а в точке В — наибольшее сжимающее напряжение. [c.334]
Внутренние силы и напряжения, возникающие в поперечных сечениях бруса при растяжении и сжатии [c.29]
Под растяжением, как указывалось в 3, понимается такой вид нагружения, при котором в поперечных сечениях бруса (стержня) возникают только нормальные силы, а все прочие внутренние силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю. [c.29]
Под кручением понимается такой вид, нагружения, при котором в поперечных сечениях бруса возникает только крутящий момент. Прочие силовые факторы (изгибающие моменты, нормальная и поперечные силы) равны нулю. [c.81]
Механизм деформирования бруса с круглым поперечным сечением можно представить себе в следующем виде будем считать, что каждое поперечное сечение бруса в результате действия внешних моментов поворачивается в своей плоскости на некоторый угол как жесткое целое. Этот угол поворота для различных сечений будет различным. Сказанное представляет собой гипотезу, т. е. предположение, оправдываемое общими правдоподобными соображениями о характере возникающих перемещений. [c.83]
Касательные напряжения в поперечных сечениях бруса направлены в каждой точке перпендикулярно к текущему радиусу р. Из условия парности следует, что точно такие же напряжения возникают и в продольных сечениях бруса (рис. 83). Наличие этих напряжений проявляется, например, при испытании на кручение деревянных образцов. [c.86]
На рис. 93 в качестве п])имера показана форма закрученного бруса прямоугольного поперечного сечения. На поверхность бруса предварительно была нанесена мелкая прямоугольная сетка, которая деформировалась вместе с поверхностными частицами металла. Поперечные линии сетки заметно искривлены, следовательно, искривлены будут и поперечные сечения бруса. [c.92]
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСА [c.106]
Возьмем некоторое поперечное сечение бруса (рис. 110). Свяжем его с,системой координат х, у и рассмотрим два следующих интеграла [c.106]
Внутренние силовые факторы, возникающие в поперечных сечениях бруса при изгибе [c.118]
Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают изгибающие моменты (см. 3). Если изгибающий момент в сечении является единствен)1ым силовым фактором, а поперечные и нормальная силы отсутствуют, [c.118]
Легко обнаружить, что совокупность точек, расположенных до изгиба в плоскости поперечного сечения бруса, после изгиба также образует плоскость, но переместившуюся в пространстве. Действительно, рассмотрим среднее поперечное сечение АА (рис. 131, а). Точки [c.125]
Свяжем теперь напряжение о с внутренними силовыми фактора.ми, возникающими в поперечном сечении бруса при чистом изгибе. [c.126]
Е результате изменения длины отдельных участков бруса его поперечные сечения получают линейные перемещения U вдоль геометрической оси. Перемещения сечений бруса отсчитываются от неподвижного сечения. Для построения эпюры С/ (J(z j надо определить перемещения текущих сечений каждого участка бруса относительно. неподвижного сечения. Они равны удлинению части бруса, заключенному между неподрижным и рассматриваемым текущим сечением. Поэтому перемещению Lifzj приписывается знак “плюс”, если рассматриваемая часть бруса удлиняется (удлинение этой части [c.8]
Еозникают ли при осевом растяжении-сжатии в поперечных сечениях бруса касательные напряжения [c.13]
Кручением называется такой вид нагружения (деформации), пои котором в поперечных сечениях бруса возникает только один внутренний силовой фактор – кпутящий момент М)(. Этот вид нагружения возникает при приложении к брусу пар сил, плоскости действия котошх перпендикулярны его оси. Такие брусья принято называть валами. [c.13]
JV главный центральный момент и[1ерции поперечного сечения бруса [c.5]
N — мощность продольная сила в поперечном сечении бруса п — коэффициент запаса прочности, угловая скорость в о61мин [c.6]
Начнем с того, что пользуясь принципом независимости действия сил, определим отдельно напряжения, возникающие в брусе при кручении, и отдельно — при изгибе. При изгибе в поперечных сечениял бруса возникают, как известно, нормальные напряжения, достигающие наибольшего значения в крайних волокнах балки а = М/Шх, и касательные напряжения, достигающие наибольшего значения у нейтральной оси и определяемые по формуле Журавского. Для круглых и вообще массивных сечений значения их незначительны по сравнению с касательными напряжениями от кручения и ими можно пренебречь. [c.253]
Надо сказать, что задача о кручении бруса может быть решена не только методами сопротивления материалов, но также и методами теории упругости без принятия каких-либо гипотез, кроме предположения о непрерывности строения вещества. Решение, полученное этим путем, показывает, что круглое поперечное сечение бруса действительно остается плоским и поворачибается как жесткое целое. В поперечных сечениях возникают только касательные напряжения. [c.83]
При решении задач, связанных с изгибом, возникает необходимость оперировать некоторыми геометрическими характеристиками поперечных сечений бруса. Эти характеристики имеют применение в основном в пределах задач изгиба и в силу своего узкого приклад-Н010 значения в общем курсе геометрии не изучаются. Их рассматривают обычно в курсе сопротивления материалов. Настоящая глава и посвящена этому вопросу. [c.106]
Рассмотрим наиболее простой случай изгиба, а именно, чистый изгиб. Под чистым изгибом, как уже указывалось, понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают только изгибающие моменты, а <3 = 0. Для тех участков бруса, где соблюдается это условие, изгибающий момент согласно второму выражению (4,1) остается постоянным (Л1 = сопз1). Условия чистого изгиба могут возникать при различных внешних нагрузках. Некоторые характерные примеры показаны на рис. 130. [c.124]
Предыдущие лекции:
Лекция 1. Вводная. Часть 1.
Лекция 1. Вводная. Часть 2.
1. Зачем нужны геометрические характеристики плоских сечений бруса
Как видно из предыдущей лекции, для того, чтобы вычислить среднее напряжение на площадке необходимо знать площадь этой площадки. Этим примером применение геометрических характеристик конечно не ограничивается. В следующих лекциях будут рассматриваться различные виды напряженного состояния: растяжение-сжатие, изгиб, срез, кручение. Для определения напряжений и деформаций в которых нужно знать геометрическин характеристики поперечных сечений, которые будут рассмотрены в этой лекции.
Для дальнейшего изучения данной темы не помешает вспомнить основы интегрального исчисления (раздел высшей математики, которую изучают на младших курсах технических ВУЗов).
Для лучшего усвоения этой темы будет полезно вспомнить раздел интегрального исчисления из курса Высшей математики и особенно кратные интегралы (в этой лекции мы будем использовать двойные интегралы).
2. Площади поперечных сечений

Универсальный способ найти площадь поперечного сечения – с помощью интеграла. На рисунке показано произвольное сечение. Поперечное сечение разбиваем на элементарные прямоугольники и сумма площадей этих элементарных прямоугольников будет приблизительно равна площади сечения. Если размер элементарного прямоугольника стремится к нулю, то получим интеграл с помощью которого можно получить точное значение площади поперечного сечения:

Здесь и далее под интегралом по области (поперечному сечению) естественно имеется в виду двойной интеграл, который в части случаев сводится к обычному определенному интегралу.
Пример 1:
Найдем площадь прямоугольного треугольника:

Самое главное в таких примерах разбить сечение на элементарные площади, записать выражение для этой элементарной площади для подстановки под интеграл и увидеть пределы интегрирования. Это касается не только этого примера, но и следующих в этой лекции.
Разобьем треугольник на элементарные прямоугольники, найдем площадь элементарного прямоугольника и составим интеграл для вычисления площади:

В итоге получили привычную формулу. Аналогично можно вычислить площади других простейших фигур. В приведенном примере для построения интеграла была использована прямоугольная декартова система координат. Иногда удобно то же самое проделать с помощью полярной системе координат, например, для определения площади полукруга.
Сечение может состоять из нескольких простых фигур, выражения для площадей или их значения известны. В этом случае интеграл можно заменить знаком суммы и площадь составной фигуры будет равна сумме площадей элементарных фигур. Очевидно, что если составная фигура имеет отверстия, то площади отверстий войдут в общую сумму со знаком “-“.
Площадь сечения всегда положительна, но площадь элементарной фигуры (отверстия) из которых состоит сечение может быть отрицательной.
3. Статические моменты площади. Центр тяжести поперечного сечения
Геометрическая характеристика статический момент площади важна как сама по себе так и в качестве инструмента для определения центра тяжести поперечного сечения. И, если площадь не зависит от положения поперечного сечения (передвинув сечение мы получим тот же результат, единственное, на что это повлияет – удобство составления интеграла), то статический момент площади вычисляется относительно оси координат и зависит от положения сечения относительно этой оси. Это видно из формул для определения статического момента площади. Статическими моментами площади называются интегралы вида (относительно осей x и y соответственно):

Статические моменты площади могут быть положительными, отрицательными, равными нулю.
Оси, относительно которых статические моменты площади равны нулю называются центральными осями.

На рисунке оси координат x и y – произвольные, yC и xC – центральные. Центр тяжести поперечного сечения лежит на центральных осях. Это свойство основано на следствии первой теореме о среднем.
Пусть функция f(x) непрерывна на отрезке [a;b]. Тогда на отрезке [a;b] найдется такая точка c, что

более подробно об этой теореме, ее доказательстве и следствиях можно прочитать на стр. 226 [1].
[1] Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу.: Учебник для университетов и пед. вузов/ Под ред. В.А. Садовничего – М.: Высш. шк. 1999. – 695 с.

Откуда можно найти координаты центра тяжести сечения:

Если сечение состоит из нескольких простых фигур, то координаты центра тяжести сечения находятся как суммы статических моментов площади деленные на площадь сечения:

Пример 2:
Найдем площадь и координаты центра тяжести сечения, состоящего из двух простых фигур двумя способами. Все размеры заданы в сантиметрах.
Способ 1 с помощью разбиения на простые фигуры. Слева показано заданное сечение, справа оно со вспомогательной системой координат и разбиением на более простые фигуры:

Вспомогательную систему координат можно выбирать произвольно, на рисунке она выбрана так, чтобы было меньше промежуточных вычислений. Затем разбиваем трапецию на прямоугольный треугольник и прямоугольник. Центр тяжести треугольника находится на пересечении медиан, а центр тяжести прямоугольника на пересечении диагоналей. Находим площади простых фигур, площадь сечения, координаты центров тяжести простых фигур. Затем вычисляем координаты центра тяжести сечения через суммы. Ход вычислений приведен ниже (расчет был сделан в бесплатной программе SMath Studio которая очень удобна для таких простых вычислений):

А теперь проделаем то же самое с помощью интегрирования. В то же время это демонстрация определения статических моментов площади с помощью интегралов. Для этого не нужно разбивать сечение на простые фигуры, но без вспомогательной системы координат так же не обойтись:

Здесь для вычисления интегралов записаны выражения функций y(x)=Kx+B, коэффициенты определены из двух уравнений по двум точкам:
x=0; y=3.1
x=3; y=1.7
и x(y)=Ky+B
эта функция кусочная, если y находится на отрезке [0;1.7], то x(y)=3
если y находится на отрезке [1.7;3.1], то коэффициенты уравнения x(y)=Ky+B находятся по тем же двум точкам.

Как видно, результат полученный разными способами совпал.
Выбор способа вычисления зависит от вида поперечного сечения.
Если размеры заданы в сантиметрах, то статические моменты площади будут выражены в кубических сантиметрах
4. Моменты инерции (осевые, центробежный и полярный)
Интегралы вида

называются осевыми моментами инерции. Для поперечного сечения они всегда положительные, а для простых фигур из которых поперечное сечение состоит могут быть отрицательными (если эта фигура является вырезом).
Интеграл вида

называется центробежным моментом инерции, он может быть положительным, отрицательным и равным нулю

Интеграл вида

называется полярным моментом инерции.
Для полярной системы координат
![]()
поэтому

В частности для круглого сечения
![]()
Пример 3:
Найдем осевые и центробежный моменты инерции для прямоугольного сечения относительно центральных осей:

Моменты инерции выражаются в единицах длины в четвертой степени. Например, если размеры заданы в метрах, то моменты инерции будут выражены в метрах в четвертой степени.

5. Понятие о радиусах инерции
Осевые радиусы инерции:

6. Моменты сопротивления
Отношение осевых моментов инерции к координатам наиболее удаленных точек сечения называется осевыми моментами сопротивления (в системе главных центральных осей – об этом понятии во второй части этой лекции):

При использовании материалов блога ссылка на источник обязательна
