Площадь поперечного сечения
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
S = πR2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a2 + b2 = c2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a2 + b2)
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S= c*h
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
S=a*b
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
S =2R*h
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
S =2а*h
где 2а – значение хорды, расчета площади поперечного сечения.
В этой статье разберемся с понятием “площадь сечения” и проанализируем справочные данные. Выбору площади поперечного сечения проводов (иначе говоря, толщины) уделяется большое внимание на практике и в теории. Ведь от площади сечения зависит сопротивление 1 метра провода, а значит – максимальный ток, ограниченный температурой нагрева, и падение напряжения на данном участке провода.
Расчет сечения провода
Строго говоря, понятие “толщина” для провода используется в разговорной речи, а более научные термины – диаметр и площадь сечения. На практике толщину провода всегда характеризуют площадью сечения.
Рассчитать сечение провода на практике можно очень просто. Зная диаметр (например, измерив его штангенциркулем), можно легко вычислить площадь сечения по формуле
S = π (D/2)², где
- S – площадь сечения провода, мм2
- π – 3,14
- D – диаметр токопроводящей жилы провода, мм. Его можно измерить, например, штангенциркулем.
Формулу площади сечения провода можно записать в более удобном виде: S = 0,8 D².
Поправка. Откровенно говоря, 0,8 – округленный коэффициент. Более точная формула: π (1/2)² = π / 4 = 0,785. Спасибо внимательным читателям 😉
Рассмотрим только медный провод, поскольку в 90% в электропроводке и электромонтаже применяется именно он. Преимущества медных проводов перед алюминиевыми – удобство в монтаже, долговечность, меньшая толщина (при том же токе).
Но с ростом диаметра (площади сечения) высокая цена медного провода съедает все его преимущества, поэтому алюминий в основном применяют там, где ток превышает значение 50 Ампер. В данном случае используют кабель с алюминиевой жилой 10 мм2 и толще.
Площадь сечения проводов измеряется в квадратных миллиметрах. Самые распространенные на практике (в бытовой электрике) площади сечения: 0,75, 1,5, 2,5, 4 мм2
Есть и другая единица измерения площади сечения (толщины) провода, применяемая в основном в США, – система AWG. На Дзене Самэлектрик.ру есть таблица сечений проводов по системе AWG и перевод из AWG в мм2.
Рекомендую почитать также мою статью про выбор сечения провода для постоянного тока там много теоретических выкладок и рассуждений о падении напряжения, сопротивлении проводов для разных сечений, и какое сечение выбрать оптимальнее для разных допустимых падений напряжения.
И ещё статья на Дзене – Падение напряжения на трехфазных кабельных линиях большой длины. приведен реальный пример объекта, приводятся формулы и рекомендации, как уменьшить потери. Потери на проводе прямо пропорциональны току и длине. И обратно пропорциональны сопротивлению.
При выборе площади сечения проводов следует руководствоваться тремя основными принципами.
- Площадь сечения провода (иначе говоря, его толщина) должна быть достаточной для прохождения через него электрического тока. Достаточной – это означает, что при прохождении максимально возможного в данном случае тока нагрев провода будет допустимым (как правило, не более 60 С)
- Сечение провода должно быть достаточным, чтобы падение напряжения на нём не превышало допустимое значение. Это особенно актуально для длинных кабельных линий (десятки и сотни метров) и больших токов.
- Толщина провода и его защитная изоляция должна обеспечивать его механическую прочность, а значит надежность.
Например, для питания люстры в гостиной используются лампочки с суммарной потребляемой мощностью 100 Вт (ток чуть более 0,5 А). Вроде бы, вполне достаточно проводов с площадью сечения 0,5 мм2? Но какой электрик в здравом уме будет закладывать такой провод в потолочную плиту? В данном случае как правило применяют 1,5 мм2.
На самом деле, выбор толщины провода зависит от одного параметра – максимальной рабочей температуры. При превышении этой температуры провод и изоляция на нём начнут плавиться и разрушаться. Иначе говоря, максимальный рабочий ток для провода с определенным сечением ограничивается только максимальной его рабочей температурой. И временем, которое сможет проработать провод в таких условиях.
Ниже дана общеизвестная таблица сечения проводов для подбора площади сечения медных проводов в зависимости от тока. Исходные данные – площадь сечения проводника.
Максимальный ток для разной толщины медных проводов
Таблица 1
(Данные из таблицы 1.3.4 ПУЭ)
Выделены номиналы проводов, используемых в бытовой электрике. “Один двужильный” – это кабель с двумя проводами, один из них – Фаза, другой – Ноль. То есть, это однофазное питание нагрузки. “Один Трехжильный” – это при трехфазном питании.
Эта таблица показывает, при каких токах и в каких условиях можно эксплуатировать провод данного сечения.
Животрепещущий пример из практики – если на розетке написано “Max.16A”, то можно для этой одной розетки проложить провод сечением 1,5мм2. Но обязательно защитить розетку автоматическим выключателем на ток не более 13А, а лучше – 10А.
В таблице одножильный провод – означает, что рядом (на расстоянии менее 5 диаметров провода) не проходит больше никаких проводов. Двужильный провод – два провода рядом, как правило, в одной общей изоляции. Это более тяжелый тепловой режим, поэтому максимальный ток меньше. И чем больше проводов в кабеле или пучке, тем меньше должен быть максимальный ток для каждого проводника из-за возможного взаимного нагрева.
Эту таблицу я считаю не совсем удобной для практики. Ведь чаще всего исходный параметр – это мощность потребителя электроэнергии, а не ток, и исходя из этого нужно выбирать провод.
Как найти ток, зная мощность? Нужно мощность Р (Вт) поделить на напряжение (В), и получим ток (А):I = P/U
Как найти мощность, зная ток? Нужно ток (А) умножить на напряжение (В), получим мощность (Вт):P = I U
Эти формулы – для случая активной нагрузки (потребители в жилах помещениях, типа лампочек и утюгов). Для реактивной нагрузки обычно используется коэффициент от 0,7 до 0,9 (в промышленности, где работают мощные трансформаторы и электродвигатели).
Предлагаю вам вторую таблицу, в которой исходные параметры – потребляемый ток и мощность, а искомые величины – сечение провода и ток отключения защитного автоматического выключателя.
Выбор толщины провода и автоматического выключателя, исходя из потребляемой мощности и тока
Ниже – таблица выбора сечения провода, исходя из известной мощности или тока. А в правом столбце – выбор автоматического выключателя, который ставится в этот провод.
Таблица 2
Красным цветом выделены критические случаи, в которых лучше перестраховаться и не экономить на проводе, выбрав провод потолще, чем указано в таблице. А ток автомата – поменьше.
Глядя в табличку, можно легко выбрать сечение провода по току, либо сечение провода по мощности.
А также – выбрать автоматический выключатель под данную нагрузку.
В этой таблице данные приведены для следующего случая.
- Одна фаза, напряжение 220 В
- Температура окружающей среды +30 С
- Прокладка в воздухе или коробе (в закрытом пространстве)
- Провод трехжильный, в общей изоляции (кабель)
- Используется наиболее распространенная система TN-S с отдельным проводом заземления
- Достижение потребителем максимальной мощности – крайний, но возможный случай. При этом максимальный ток может действовать длительное время без отрицательных последствий.
Если температура окружающей среды будет на 20 С выше, или в жгуте будет несколько кабелей, то рекомендуется выбрать большее сечение (следующее из ряда). Особенно это касается тех случаев, когда значение рабочего тока близко к максимальному.
Вообще, при любых спорных и сомнительных моментах, например
- возможное в будущем увеличение нагрузки
- большие пусковые токи
- большие перепады температур (электрический провод на солнце)
- пожароопасные помещения
нужно либо увеличивать толщину проводов, либо более детально подойти к выбору – обратиться к формулам, справочникам. Но, как правило, табличные справочные данные вполне пригодны для практики.
Таблица зависимости тока защитного автомата (предохранителя) от сечения
(Дополнение к статье)
А вот как к максимальному току в зависимости от площади сечения провода относятся немцы. В правом столбце – рекомендация по выбору автоматического (защитного) выключателя.
Таблица 3
Как видно, немцы перестраховываются, и предусматривают больший запас по сравнению с нами.
Хотя, возможно, это от того, что таблица взята из инструкции из “стратегического” промышленного оборудования.
Хорошая советская книга на тему статьи:
• Карпов Ф. Ф. Как выбрать сечение проводов и кабелей, 1973 год / Брошюра из Библиотеки электромонтера. Приведены указания и расчеты, необходимые для выбора сечений проводов и кабелей до 1000 В. Полезно для тех, кто интересуется первоисточниками., zip, 1.57 MB, скачан: 2949 раз./
Источник статьи
——————————————————————-
Статья заинтересовала? Лайк, подписка, комментарий!
Ещё больше статей на канале СамЭлектрик.ру
и на блоге СамЭлектрик.ру.
Спасибо, что читаете меня! Мне тоже интересно то, о чем я пишу!
Пожалуйста, будьте вежливы и уважайте мнение автора и читателей! Хейтеров отправляю в баню.
Внимание!
Автор не гарантирует, что всё написанное на этой странице – истина.
За ваши действия и за вашу безопасность ответственны только вы!

Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.
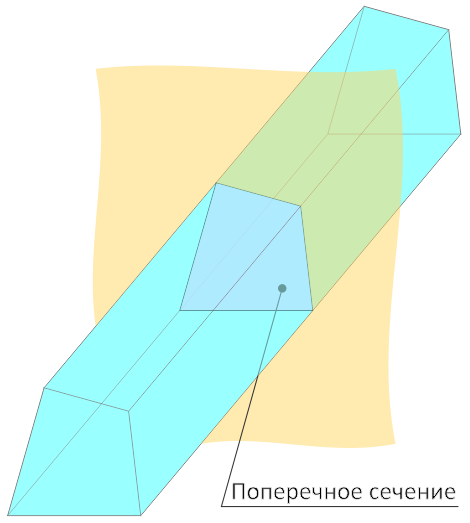
Сечение может иметь простую или сложную форму, а также быть составным.
Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.
Площадь поперечного сечения
В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.
Формулы для расчета площади основных фигур.
Пример:
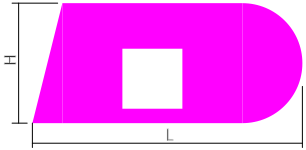
Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением.

Для расчета общей площади, сложное сечение раскладывается на простые фигуры:
Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто.

В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:
A=A1+A2+A3-A4
Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.
Площадь составного сечения
Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым.

Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.
Эти сечения сами по себе тоже являются сложными.
Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.
В результате сложив все составляющие профили, получим площадь всего сечения.
Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.
Длина поперечного сечения
Длиной поперечного сечения называют полную (габаритную) длину фигуры как расстояние по горизонтали между двумя её наиболее удаленными точками.
Длина поперечного сечения обозначается латинской буквой L или l и измеряется стандартно в миллиметрах или сантиметрах.
Ширина сечения определяется аналогично, но обозначается буквой H или h.
При решении задач, длину, ширину и площади поперечного сечения рекомендуется переводить соответственно в метры и м2.
Понятие «поперечное сечение» является одним из основных при расчетах на прочность в сопротивлении материалов и технической механике.
Различают два основных вида расчета площади сечений:
- Геометрический — когда требуется найти площадь сечения тела по известным размерам;
- Прочностной — расчет площади поперечного сечения бруса проводится по условию прочности.
Пример расчета поперечных сечений >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Как вычислить площадь поперечного сечения
Поперечное сечение образуется под прямым углом по отношению к продольной оси. Причем, сечение разных геометрических фигур представлено может быть различными формами. К примеру, у параллелограмма сечение по внешнему виду напоминает прямоугольник или квадрат, у цилиндра – прямоугольник или круг и т.д.
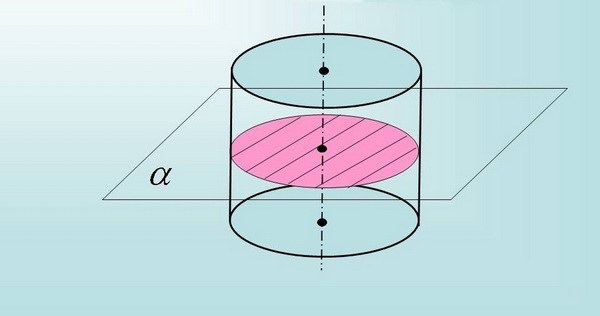
Вам понадобится
- – калькулятор;
- – исходные данные.
Инструкция
Чтобы найти площадь сечения параллелограмма, нужно знать значение его основания и высоту. Если, к примеру, известна лишь длина и ширина основания, то найдите диагональ, используя для этого теорему Пифагора (квадрат длины гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов: a2 + b2 = c2). Ввиду этого, c = sqrt (a2 + b2).
Найдя значение диагонали, подставьте его в формулу S= c*h, где h – высота параллелограмма. Полученный результат и будет величиной площадью поперечного сечения параллелограмма.
Если же сечение проходит вдоль двух оснований, то его площадь рассчитывайте по формуле: S=a*b.
Для вычисления площади осевого сечения цилиндра, проходящей перпендикулярно основаниям (при условии, что одна сторона этого прямоугольника равна радиусу основания, а вторая – высоте цилиндра), используйте формулу S =2R*h, в которой R – величина радиуса окружности (основания), S – площадь поперечного сечения, а h – высота цилиндра.
Если по условиям задачи сечение не проходит через ось вращения цилиндра, но при этом параллельно его основаниям, значит, сторона прямоугольника не будет равна диаметру окружности основания.
Самостоятельно вычислите неизвестную сторону путем построения окружности основания цилиндра, проведения перпендикуляров от стороны прямоугольника (плоскости сечения) к окружности и расчета размера хорды (по теореме Пифагора). После этого подставьте в S =2а*h полученное значение (2а – значение хорды) и рассчитайте площадь поперечного сечения.
Площадь сечения шара определяется по формуле S = πR2. Обратите внимание на то, что, если расстояние от центра геометрической фигуры до плоскости будет совпадать с плоскостью, то площадь сечения равна будет нулю, потому как шар касается плоскости лишь в одной точке.
Обратите внимание
Дважды пересчитывайте полученный результат: так вы не допустите ошибки в расчетах.
Полезный совет
Чтобы рассчитать площадь сечения любой другой геометрической фигуры, воспользуйтесь математическим справочником, в котором подобраны формулы для расчета и даны подробные рекомендации.
Источники:
- Стереометрия. Теория
- поперечное сечение
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
You may encounter situations in which you have a three-dimensional solid shape and need to figure out the area of an imaginary plane inserted through the shape and having borders defined by the boundaries of the solid.
For example, if you had a cylindrical pipe running under your home measuring 20 meters (m) in length and 0.15 m across, you might want to know the cross-sectional area of the pipe.
Cross sections can be perpendicular to the orientation of the axes of the solid if any exist. In the case of a sphere, any cutting plane through the sphere regardless of orientation will result in a disk of some size.
The area of the cross-section depends on the shape of the solid determining the cross-section’s boundaries and the angle between the solid’s axis of symmetry (if any) and the plane that creates the cross section.
Cross-Sectional Area of a Rectangular Solid
The volume of any rectangular solid, including a cube, is the area of its base (length times width) multiplied by its height: V = l × w × h.
Therefore, if a cross section is parallel to the top or bottom of the solid, the area of the cross-section is l × w. If the cutting plane is parallel to one of the two sets the sides, the cross-sectional area is instead given by l × h or w × h.
If the cross-section is not perpendicular to any axis of symmetry, the shape created may be a triangle (if placed through a corner of the solid) or even a hexagon.
Example: Calculate the cross-sectional area of a plane perpendicular to the base of a cube with a volume of 27 m3.
-
Since l = w = h for a cube, any one edge of the cube must be 3 m long (since 3
× 3
× 3 = 27). A cross-section of the type described would therefore be a square 3 m on a side, giving an area of 9 m2.
Cross-Sectional Area of a Cylinder
A cylinder is a solid created by extending a circle through space perpendicular to its diameter. The area of a circle is given by the formula πr2, where r is the radius. It therefore makes sense that the volume of a cylinder would be the area of one of the circles forming its base.
If the cross-section is parallel to the axis of symmetry, then the area of the cross-section is simply a circle with an area of πr2. If the cutting plane is inserted at a different angle, the shape generated is an ellipse. The area uses the corresponding formula: πab (where a is the longest distance from the center of the ellipse to the edge, and b is the shortest).
Example: What is the cross-sectional area of the pipe under your home described in the introduction?
-
This is just πr2 = π(0.15 m)2=
π(0.0225) m2 = 0.071 m2. Note that the length of the pipe is irrelevant to this calculation.
Cross-Sectional Area of a Sphere
Any theoretical plane placed through a sphere will result in a circle (think about this for a few moments). If you know either the diameter or the circumference of the circle the cross-section forms, you can use the relationships C = 2πr and A = πr2 to obtain a solution.
Example: A plane is rudely inserted through the Earth very close to the North Pole, removing a section of the planet 10 m around. What is the cross-sectional area of this chilly slice of Earth?
- Since C = 2πr = 10 m, r = 10/2π = 1.59 m; A = πr2= π(1.59)2= 7.96 m2.
