{S = pi (R^2 – r^2)}
С помощью приведенных калькулятора и формул можно рассчитать площадь кольца через радиусы или диаметры онлайн.
Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.
Содержание:
- калькулятор площади кольца
- формула площади кольца через радиусы
- формула площади кольца через диаметры
- примеры задач
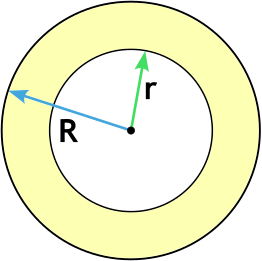
Формула площади кольца через радиусы
{S = pi (R^2 – r^2)}
R – внешний радиус кольца
r – внутренний радиус кольца
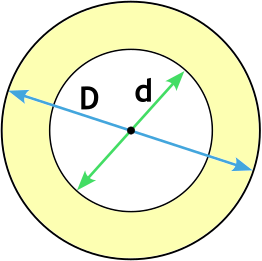
Формула площади кольца через диаметры
{S= dfrac{pi}{4}(D^2 – d^2)}
D – внешний диаметр кольца
d – внутренний диаметр кольца
Примеры задач на нахождение площади кольца
Задача 1
Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.
Решение
В условии задачи даны радиусы ограничивающих кольцо окружностей, поэтому воспользуемся первой формулой.
S = pi (R^2 – r^2) = pi (7^2 – 3^2) = pi (49 – 9) = 40pi approx 125.66371 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Полученный ответ можно проверить с помощью калькулятора .
Задача 2
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны dfrac{4}{sqrt{pi}} и dfrac{2}{sqrt{pi}}.
Решение
Задача похожа на предыдущую, поэтому алгоритм ее решения будет тот же.
S = pi (R^2 – r^2) = pi ({Big(dfrac{4}{sqrt{pi}} Big) }^2 – {Big(dfrac{2}{sqrt{pi}} Big) }^2) = pi (dfrac{16}{pi} – dfrac{4}{pi}) = pi dfrac{12}{pi} = 12 : см^2
Ответ: 12 : см^2
Наш калькулятор может производить вычисления с выражениями. Для того, чтобы ввести радиусы из условия их нужно записать в понятном для калькулятора формате:
dfrac{4}{sqrt{pi}} : rarr : 4/sqrt(pi)
dfrac{2}{sqrt{pi}} : rarr : 2/sqrt(pi)
Если ввести данные в таком формате, можно проверить ответ .
Задача 3
Найдите площадь кольца образованного двумя окружностями с общим центром если радиусы равны 15 и 13.
Решение
Задача аналогична предыдущим.
S = pi (R^2 – r^2) = pi (15^2 – 13^2) = pi (225 – 169) = 56pi approx 175.92919 : см^2
Ответ: 56pi approx 175.92919 : см^2
Проверка .
Задача 4
Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.
Решение
Задача аналогична предыдущим.
S = pi (R^2 – r^2) = pi (13^2 – 12^2) = pi (169 – 144) = 25pi approx 78.53982 : см^2
Ответ: 25pi approx 78.53982 : см^2
Проверка .
Как рассчитать площадь кольца
На данной странице калькулятор поможет рассчитать площадь кольца онлайн. Для расчета задайте внутренние и внешние радиусы или диаметры.
Через радиусы
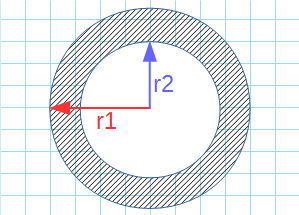
Формула для нахождения площади кольца через внешний и внутренний радиус:
π – константа равная (3.14); r1 – внешний радиус; r2 – внутренний радиус.
Через диаметры
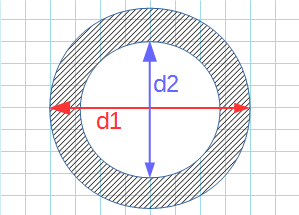
Формула для нахождения площади кольца через внешний и внутренний диаметр:
π – константа равная (3.14); d1 – внешний диаметр; d2 – внутренний диаметр.
Площадь кольца
Онлайн калькулятор
Площадь кольца по радиусам или диаметрам
Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
у внутренней окружности
Площадь кольца по толщине и любому другому параметру
Чему равна площадь кольца ограниченного двумя окружностями, если:
толщина кольца t =
Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² – 2²) = 3.14 ⋅ (9 – 4) = 3.14 ⋅ 5 = 15.7 см²
Ответ: S = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² – 2²) = 0.785 ⋅ (16 – 4) = 9.42 см²
Ответ: S = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² – (5 – 2 ⋅ 2)²) = 0.785 ⋅ (25 – 1) = 18.84 см²
Площадь круга: как найти, формулы
О чем эта статья:
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Ответ: 113,04 см 2 .
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Ответ: 6358,5 мм 2 .
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Ответ: 18,84 см 2 .
Задача: определить площадь кольца, если известны радиусы
Условие задачи:
Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.
Дано:
Радиус внешней окружности, R = 10 см
Радиус внутренней окружности, r = 8 см
Пояснение к рисунку:
O – общий центр окружностей
Найти площадь кольца: S
Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.
Формула площади внешнего круга.
Формула площади внутреннего круга.
После подстановки и преобразования, получаем следующее выражение для площади кольца.
Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/ploshad-kruga
http://www-formula.ru/zadacha/solve-area-annulus-know-radius
[/spoiler]
Содержание
- Площадь кольца
- Онлайн калькулятор
- Площадь кольца по радиусам или диаметрам
- Площадь кольца по толщине и любому другому параметру
- Теория
- Площадь кольца через радиусы
- Формула
- Пример
- Площадь кольца через диаметры
- Формула
- Пример
- Площадь кольца через толщину
- Формулы
- Пример
- Площадь кольца
- Формула площади кольца через радиусы
- Формула площади кольца через диаметры
- Примеры задач на нахождение площади кольца
- Онлайн калькулятор для расчета площади кольца
- Расчет площади кольца через внешний и внутренний радиус
- Расчет площади кольца через внешний и внутренний диаметр
- Калькулятор онлайн расчета площади кольца по заданным радиусам или диаметрам.
- 01) Площадь кольца по радиусам большего и меньшего круга
- 02) Площадь кольца по диаметрам большего и меньшего круга
- Как найти площадь кольца ограниченного двумя окружностями
- Площадь кольца
- Онлайн калькулятор
- Площадь кольца по радиусам или диаметрам
- Площадь кольца по толщине и любому другому параметру
- Теория
- Площадь кольца через радиусы
- Формула
- Пример
- Площадь кольца через диаметры
- Формула
- Пример
- Площадь кольца через толщину
- Формулы
- Пример
- Найти площадь кольца образованного двумя окружностями
- Площадь кольца
- Онлайн калькулятор
- Площадь кольца по радиусам или диаметрам
- Площадь кольца по толщине и любому другому параметру
- Теория
- Площадь кольца через радиусы
- Формула
- Пример
- Площадь кольца через диаметры
- Формула
- Пример
- Площадь кольца через толщину
- Формулы
- Пример
- Задача: определить площадь кольца, если известны радиусы
- Условие задачи:
- Найти площадь кольца: S
- Ответ:
- Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами R1 и R2, R12
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Задача: определить площадь кольца, если известны радиусы
- Условие задачи:
- Найти площадь кольца: S
- Ответ:
Площадь кольца
Онлайн калькулятор
Площадь кольца по радиусам или диаметрам
Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
у внутренней окружности
Площадь кольца по толщине и любому другому параметру
Чему равна площадь кольца ограниченного двумя окружностями, если:
Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² — 2²) = 3.14 ⋅ (9 — 4) = 3.14 ⋅ 5 = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² — 2²) = 0.785 ⋅ (16 — 4) = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² — (5 — 2 ⋅ 2)²) = 0.785 ⋅ (25 — 1) = 18.84 см²
Источник
Площадь кольца
С помощью приведенных калькулятора и формул можно рассчитать площадь кольца через радиусы или диаметры онлайн.
Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.
Содержание:
Формула площади кольца через радиусы
R — внешний радиус кольца
r — внутренний радиус кольца
Формула площади кольца через диаметры
D — внешний диаметр кольца
d — внутренний диаметр кольца
Примеры задач на нахождение площади кольца
В условии задачи даны радиусы ограничивающих кольцо окружностей, поэтому воспользуемся первой формулой.
S = pi (R^2 — r^2) = pi (7^2 — 3^2) = pi (49 — 9) = 40pi approx 125.66371 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Полученный ответ можно проверить с помощью калькулятора .
Задача похожа на предыдущую, поэтому алгоритм ее решения будет тот же.
Наш калькулятор может производить вычисления с выражениями. Для того, чтобы ввести радиусы из условия их нужно записать в понятном для калькулятора формате:
Если ввести данные в таком формате, можно проверить ответ .
Задача аналогична предыдущим.
S = pi (R^2 — r^2) = pi (15^2 — 13^2) = pi (225 — 169) = 56pi approx 175.92919 : см^2
Ответ: 56pi approx 175.92919 : см^2
Задача аналогична предыдущим.
S = pi (R^2 — r^2) = pi (13^2 — 12^2) = pi (169 — 144) = 25pi approx 78.53982 : см^2
Источник
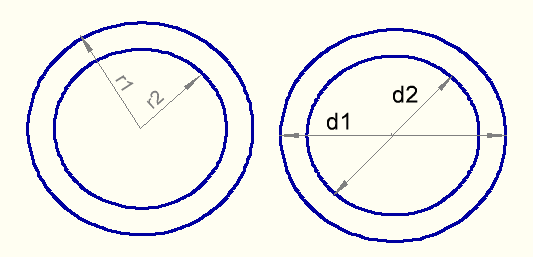
Онлайн калькулятор для расчета площади кольца
Расчет площади кольца производится через внешний (r1) и внутренний (r2) радиус, а так же через внешний (d1) и внутренний (d2) диаметр. Внешний и внутренний диаметр, внешний и внутренний радиус в онлайн калькуляторе безразмерные величины, если ответ Вам нужен в кв. мм, то все величины задаваемые для расчета должны быть в мм. Так же для удобства Вы можете задать кол-во знаков после запятой в ответе.
Расчет площади кольца через внешний и внутренний радиус
Расчет площади кольца через внешний и внутренний диаметр
Калькулятор для расчета площади кольца
Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями. Площадь кольца, ограниченного окружностями радиусов R и r, определяется как разность площадей кругов с такими радиусами: Площадь кольца также может быть вычислена путём умножения числа пи на квадрат половины длины самого большого отрезка, лежащего внутри кольца. Это можно доказать через теорему Пифагора — такой отрезок будет являться касательной к кругу меньшего радиуса. Половина длины отрезка с.
Онлайн калькулятор для расчета площади сектора кольца
Сектор кольца – это часть круга, ограниченная дугами разных радиусов, проведенных из одной точки, и двумя радиусами, проведенными к концам большей дуги. Расчет площади сектора кольца производится через внешний (r1) и внутренний (r2) радиус и угол сегмента круга. Внешний и внутренний диаметр сегмента круга в онлайн калькуляторе безразмерные величины, если ответ Вам нужен в кв. мм, то все величины задаваемые для расчета должны быть в мм. Так же для удобства Вы можете задать кол-во знаков после.
Расчет числа витков катушки на тороидальном ферритовом сердечнике
Маркировка размеров кольцевых сердечников Сначала цифрами указывается величина начальной магнитной проницаемости, затем марка используемого материала, и потом размер кольца в миллиметрах: 2000НН D x d x h Где — 2000 величина начальной магнитной проницаемости, НН – марка материала, D – внешний диаметр, d – внутренний диаметр, h – толщина кольца, все размеры в миллиметрах. Для более простых расчетов стоит воспользоваться оценочными формулами, позволяющими получить приближенные значения.
Тороидальный сварочный трансформатор из доступных материалов
Многим известно что массогабаритные характеристики у тороидов намного лучше, чем у Ш и П — образных трансформаторов (1,3-1,5 раза). Конструкция предполагает использование отслуживших срок промышленных сварочных трансформаторов, для этого его разбирают и и пластин 90 на 450 мм собирают бублик. подойдут такие трансформаторы как — ТС270 или ТСА310. Для изготовления бублика необходимо склепать обруч из пластин, внешним диаметром 260 мм. Затем внутрь обруча вставляют первую пластину, придерживая ее.
Устройство для наматывания катушек и трансформаторов на основе швейной машины
Г.М.Билецкий, г.Черновцы При изготовлении различных устройств часто возникает необходимость изготовления различных намоточных узлов (трансформаторов, дросселей и др.). При отсутствии специальных станков их приходится наматывать вручную. Изготовить катушку из нескольких витков не составляет труда, но изготовление высококачественного трансформатора или высокоиндуктивного дросселя — достаточно долгая и кропотливая работа. Я предлагаю в качестве намоточного станка использовать обычную.
Источник
Калькулятор онлайн расчета площади кольца по заданным радиусам или диаметрам.
Калькулятора онлайн рассчитывает площадь кольца и выводит формулы с подробным решением:
- по радиусам: площадь кольца равна произведению числа π на разность квадратов внешнего и внутреннего радиусов кольца;
- по диаметрам: площадь кольца равна произведение одной четвертой числа π на разность квадратов внешнего и внутреннего диаметров кольца.
01) Площадь кольца по радиусам большего и меньшего круга
расчет площади кольца по радиусам большего и меньшего круга
02) Площадь кольца по диаметрам большего и меньшего круга
расчет площади кольца по диаметрам большего и меньшего круга
| Исходные данные: | Решение: |
 |
|
| Радиус меньшего круга кольца | r = |
| Диаметр меньшего круга кольца | d = |
1. Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.
2. Площадь кольца, ограниченного окружностями радиусов R и r, определяется как разность площадей кругов с такими же радиусами.
3. Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
- Блок исходных данных выделен желтым цветом , блок промежуточных вычислений выделен голубым цветом , блок решения выделен зеленым цветом .
Источник
Как найти площадь кольца ограниченного двумя окружностями
Площадь кольца
Онлайн калькулятор
Площадь кольца по радиусам или диаметрам
Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
у внутренней окружности
Площадь кольца по толщине и любому другому параметру
Чему равна площадь кольца ограниченного двумя окружностями, если:
Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² — 2²) = 3.14 ⋅ (9 — 4) = 3.14 ⋅ 5 = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² — 2²) = 0.785 ⋅ (16 — 4) = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² — (5 — 2 ⋅ 2)²) = 0.785 ⋅ (25 — 1) = 18.84 см²
Найти площадь кольца образованного двумя окружностями
Площадь кольца
Онлайн калькулятор
Площадь кольца по радиусам или диаметрам
Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
у внутренней окружности
Площадь кольца по толщине и любому другому параметру
Чему равна площадь кольца ограниченного двумя окружностями, если:
Теория
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² — 2²) = 3.14 ⋅ (9 — 4) = 3.14 ⋅ 5 = 15.7 см²
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² — 2²) = 0.785 ⋅ (16 — 4) = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² — (5 — 2 ⋅ 2)²) = 0.785 ⋅ (25 — 1) = 18.84 см²
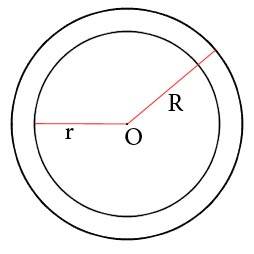
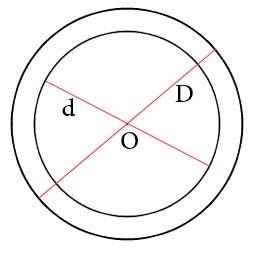
Задача: определить площадь кольца, если известны радиусы
Условие задачи:
Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.
Дано:
Радиус внешней окружности, R = 10 см
Радиус внутренней окружности, r = 8 см
Пояснение к рисунку:
O — общий центр окружностей
Найти площадь кольца: S
Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.
Формула площади внешнего круга.
Формула площади внутреннего круга.
После подстановки и преобразования, получаем следующее выражение для площади кольца.
Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами R1 и R2, R12
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,900
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Задача: определить площадь кольца, если известны радиусы
Условие задачи:
Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.
Дано:
Радиус внешней окружности, R = 10 см
Радиус внутренней окружности, r = 8 см
Пояснение к рисунку:
O — общий центр окружностей
Найти площадь кольца: S
Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.
Формула площади внешнего круга.
Формула площади внутреннего круга.
После подстановки и преобразования, получаем следующее выражение для площади кольца.
Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Источник
При помощи нашего калькулятора вы легко сможете узнать площадь кольца.
Для того что бы вычислить площадь кольца необходимо знать его внутренний и внешний радиус или внутренний и внешний диаметр. Если нам известны указанные величины, для нас не составит труда вычислить площадь кольца.
Площадь кольца рассчитывается по следующим формулам:
- Если нам известен радиус:
Формула для расчета площади кольца через радиус:
S=π(R2-r2)
- Если нам известен диаметр:
Формула для расчета площади кольца через диаметр:
S=π/4(D2-d2)
Где S – площадь кольца, R – внешний радиус кольца, r – внутренний радиус кольца, D – внешний диаметр кольца, d – внутренний диаметр кольца, π – число Пи которое всегда примерно равно 3,14.
