Как найти площадь поперечного сечения шара

Как найти площадь сечения шара

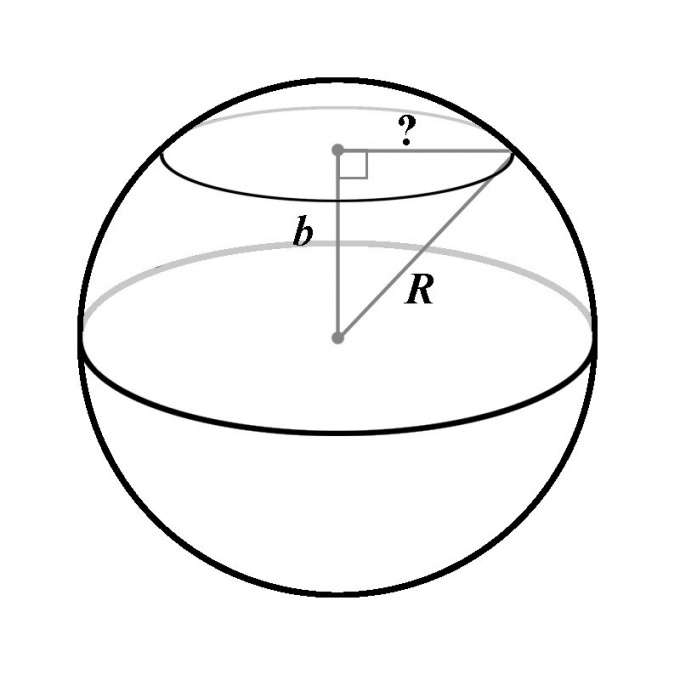
Пусть дан шар с радиусом R, который на некотором расстоянии b от центра пересекает плоскость. Расстояние b меньше или равно радиусу шара. Требуется найти площадь S получающегося при этом сечения.

Инструкция

Очевидно, что если расстояние от центра шара до плоскости равно радиусу плоскости, то плоскость касается шара только в одной точке, и площадь сечения будет равна нулю, то есть если b = R, то S = 0. Если b = 0, то секущая плоскость проходит через центр шара. В этом случае сечение будет представлять собой круг, радиус которого совпадает с радиусом шара. Площадь этого круга будет, согласно формуле, равна S = πR^2.

Эти два крайних случая дают границы, между которыми всегда будет лежать искомая площадь: 0 < S < πR^2. При этом любое сечение шара плоскостью всегда является кругом. Следовательно, задача сводится к тому, чтобы найти радиус окружности сечения. Тогда площадь этого сечения вычисляется по формуле площади круга.

Поскольку расстояние от точки до плоскости определяется как длина отрезка, перпендикулярного плоскости и начинающегося в точке, второй конец этого отрезка будет совпадать с центром окружности сечения. Такой вывод вытекает из определения шара: очевидно, что все точки окружности сечения принадлежат сфере, а следовательно, лежат на равном расстоянии от центра шара. Это значит, что каждая точка окружности сечения может считаться вершиной прямоугольного треугольника, гипотенузой которого служит радиус шара, одним из катетов — перпендикулярный отрезок, соединяющий центр шара с плоскостью, а вторым катетом — радиус окружности сечения.

Из трех сторон этого треугольника заданы два — радиус шара R и расстояние b, то есть гипотенуза и катет. По теореме Пифагора длина второго катета должна быть равна √(R^2 – b^2). Это и есть радиус окружности сечения. Подставляя найденное значение радиуса в формулу площади круга, легко прийти к выводу, что площадь сечения шара плоскостью равна:S = π(R^2 – b^2).В частных случаях, когда b = R или b = 0, выведенная формула полностью согласуется с уже найденными результатами.

Видео по теме

Источники:

• сечение шара плоскостью

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Напомним,
что шаром называется тело, состоящее из всех точек пространства,
находящихся на расстоянии не большем заданного от некоторой данной точки. Эта
точка – центр шара, а заданное расстояние – радиус шара.

Шар
так же, как цилиндр и конус, является телом вращения. Он получается в
результате вращения полукруга вокруг его диаметра.

Поверхность,
образуемая при этом вращении полуокружности, называется сферой. Можно
сказать, что сфера – это как бы оболочка, или граница, шара. Как окружность
есть граница круга, так и сфера – это граница шара.

Назовём
элементы сферы и шара.

Радиус
сферы – это отрезок, соединяющий центр сферы и любую её точку.

Хорда
сферы – отрезок, соединяющий две точки сферы.

Диаметр
сферы – хорда сферы, проходящая через её центр.

Радиус,
хорда, диаметр шара – это радиус, хорда, диаметр его сферы.

Любое
сечение шара плоскостью есть круг. Центром этого круга является основание
перпендикуляра, опущенного из центра шара на секущую плоскость.

Плоскость,
которая проходит через центр шара, называется диаметральной плоскостью.
Сечение ею шара – большим кругом, а сечение сферы – большой
окружностью.

Любая
диаметральная плоскость шара является его плоскостью симметрии. Центр
шара является его центром симметрии.

Плоскость,
проходящая через точку А сферы и перпендикулярно радиусу, проведённому в
эту точку, называется касательной плоскостью. Точка А называется точкой
касания.

Свойство
касательной плоскости к сфере: радиус сферы,
проведённый в точку касания, перпендикулярен касательной плоскости.

Признак
касательной плоскости к сфере: плоскость,
перпендикулярная радиусу сферы в конечной его точке на сфере, является
касательной к сфере.

Касательная
плоскость пересекается с шаром в единственной точке – в точке касания.

Касательной
прямой к сфере (шару) называется прямая, имеющая со сферой
единственную общую точку.

Отрезки
касательных к сфере, проведённые из одной точки, равны и составляют равные углы
с прямой, проходящей через эту точку и центр сферы.

Линией
пересечения двух сфер является окружность.

Площадь
сферы радиуса : .

Объём
шара
радиуса : .

Шаровым
сегментом называется часть шара, отсекаемая от него плоскостью.
Площадь боковой поверхности шарового сегмента:

 .

Объём
шарового сегмента:

,

где
 –
радиус шара,  –
высота шарового сегмента.

Шаровым
сектором называется тело, которое получается из шарового
сегмента и конуса, основанием которого является сечение плоскостью данного шара.

Площадь
боковой поверхности шарового сектора:

 .

Объём
шарового сектора:

,

где
 –
радиус шара,  –
высота сегмента.

Шар
называется вписанным в многогранник, а многогранник – описанным около
шара, если поверхность шара касается всех граней многогранника.

Шар
называется описанным около многогранника, а многогранник – вписанным
в шар, если поверхность шара проходит через все вершины многогранника.

Шар
называется вписанным в цилиндр, а цилиндр – описанным около шара,
если поверхность шара касается оснований цилиндра и всех образующих.

Шар
называется описанным около цилиндра, если окружности оснований цилиндра
принадлежат поверхности шара.

Шар
называется вписанным в конус (усечённый конус), а конус
(усечённый конус) – описанным около шара, если поверхность шара касается
основания (оснований) конуса и всех образующих.

Шар
называется описанным около конуса (усечённого конуса), если окружность
основания и вершина (окружности оснований) конуса принадлежат поверхности шара.

Если
боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую
пирамиду можно вписать шар.

Около
пирамиды можно описать шар тогда и только тогда, когда около её основания можно
описать окружность.

Если
боковые рёбра пирамиды равны между собой (или одинаково наклонены к плоскости
основания), то около такой пирамиды можно описать шар.

В
призму можно вписать шар тогда и только тогда, когда в перпендикулярное
сечение этой призмы можно вписать окружность, а высота призмы равна диаметру
окружности, вписанной в это перпендикулярное сечение.

Описать
шар около призмы можно тогда и только тогда, когда призма прямая и около её основания
можно описать окружность.

Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.

Задача
первая. Радиус шара увеличили в  раза.
Во сколько раз увеличился объём шара?

Решение.

Задача
вторая. Объём шара равен  см³.
Найдите диаметр шара.

Решение.

Задача
третья. Шар пересечен плоскостью. Площадь сечения равна  см².
Расстояние от центра шара до плоскости сечения равно  см.
Найдите площадь поверхности шара.

Решение.

Задача
четвёртая. В конус с радиусом основания, равным  см,
и высотой, равной  см,
вписан шар. Найдите отношение площади боковой поверхности конуса к площади
поверхности шара.

Решение.

Задача
пятая. Найдите объём шарового сектора, если радиус
окружности его основания равен  см,
а радиус шара –  см.

Решение.

Задача
шестая. Шар с радиусом  см
пересечён плоскостью, находящейся на расстоянии  см
от центра шара. Найдите площадь сечения.

Решение.

Площадь поперечного сечения

При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:

S = πR²

При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.

Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:

a² + b² = c²

Из нее можно вывести такую формулу:

c = S*q*r*t*(a² + b²)

Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:

S= c*h

S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:

S=a*b

используется в тех случаях, когда сечение идет параллельно двум основаниям.

При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:

S =2R*h

где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.

Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:

S =2а*h

где 2а – значение хорды, расчета площади поперечного сечения.