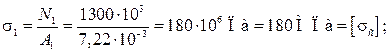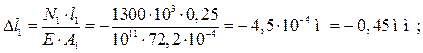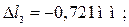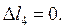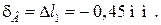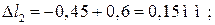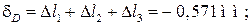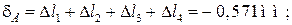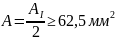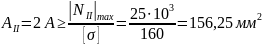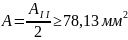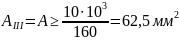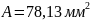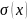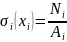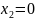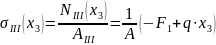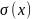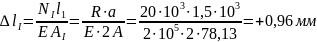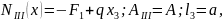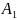Пример 1. Определить площадь поперечных сечений на всех участках чугунного стержня (рис



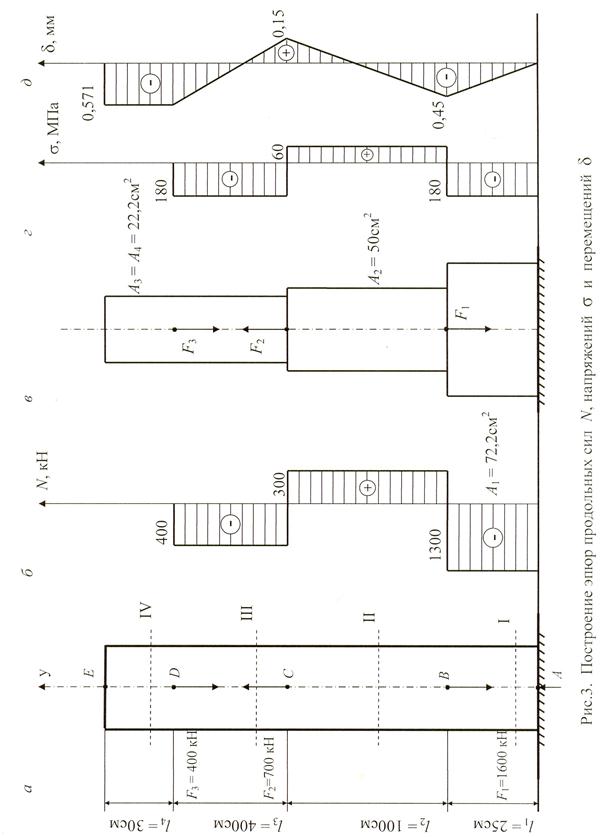
Определить площадь поперечных сечений на всех участках чугунного стержня (рис. 3, а). Построить эпюры продольных сил N, напряжений σ и перемещений δ. Принять для чугуна [σс] = 180 МПа, [σр] = 60 МПа, Е = 10 5 МПа = 10 11 Па.
Рассматриваемый стержень имеет одну опорную реакцию R, и для него можно составить лишь одно уравнение статики: Σ Y = 0. Значит, эта система статически определима:
Стержень подвергается растяжению – сжатию. Выделяем участки нагружения 1 – 4 (между точками приложения внешних сил), в пределах которых намечаются сечения I – IV.
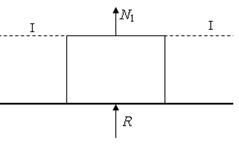
Для определения N 1 на первом участке рассмотрим равновесие части стержня, расположенной ниже сечения I – I. На нее действует реакция R (рис. 4). Уравнение статики Σ Y = 0 имеет вид
Полученный в результате подсчета знак минус при N 1 указывает,
что N 1 имеет направление, противоположное заданному, и что первый участок сжат.
Рис. 4. Определение внутренних сил N 1
На часть стержня, расположенную ниже сечения II — II, действуют реакция R и сила F 1. Тогда продольная сила в сечении II — II равна
Аналогично определяются N 3, N 4: N 3 = – 400 кН; N 4 = 0. По вычисленным значениям N строится эпюра продольных сил (см. рис. 3, б).
Из условия прочности 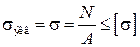
A 1 = 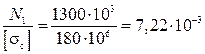
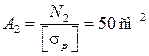
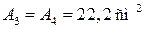
Вычисления сделайте самостоятельно.
Рассчитываемый стержень с найденными площадями поперечных сечений показан на рис.3, в.
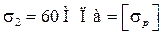
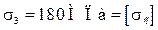
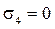
Проделанные расчеты напряжений являются проверочными.
На рис. 3, г показана эпюра нормальных напряжений. Вычислим
деформации участков стержня:
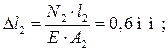
Перемещение любого сечения стержня равно сумме деформаций участков, расположенных между сечением и опорой.
Перемещение δ А точки А: δ А = 0. Перемещение точки В обусловлено деформацией участка I:
Перемещение точки С складывается из деформаций участков I и II:
Перемещение точки D складывается из деформаций участков I, II
Перемещение точки E складывается из деформаций участков I, II, III
По вычисленным значениям δ строится эпюра перемещений (см. рис. 3, д).
Задача 1. Растяжение и сжатие
(статически определимая система)
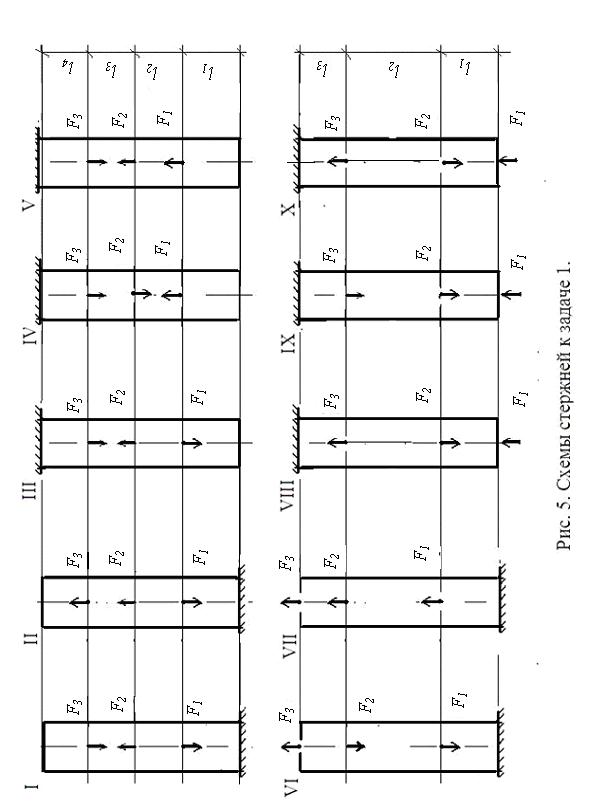
Произвести расчет стержня постоянного поперечного сечения (рис. 5) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σ], равным 210 МПа и модулем продольной упругости Е, равным 200 ГПа. Данные к задаче приведены в табл. 1.
1) вычислить продольные силы на участках стержня и построить эпюру N;
2) определить размеры поперечного сечения (сторону квадрата или диаметр);
3) вычислить нормальные напряжения на участках стержня и построить эпюру σ по длине стержня;
4) вычислить деформацию участков стержня и построить эпюру перемещений δ.
| Номер строки | Номер схемы | Нагрузка, кН | Длина участков, см | Форма сечения | |||
| F 1 | F 2 | F 3 | l1 , l4 | l2 | l3 | ||
| I | Круг | ||||||
| II | Квадрат | ||||||
| III | Круг | ||||||
| IV | Квадрат | ||||||
| V | Круг | ||||||
| VI | Квадрат | ||||||
| VII | Круг | ||||||
| VIII | Квадрат | ||||||
| IX | Круг | ||||||
| X | Квадрат | ||||||
| в | а | б | в | а | б | в | в |
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Самое популярное на сайте:
Движение декабристов. Причины возникновение движения декабристов: Причины возникновение движения декабристов: — отказ власти от проведения реформ (ликвидации крепостного права и ограничения.
Стропильные и подстропильные конструкции Железобетонные балки скатных покрытий перекрывают пролеты 12 и 18 м, железобетонные фермы – 18 и 24 м.
Нормирование труда Сущность нормирования труда. Задачи и методы технического нормирования. Виды норм затрат труда. Рабочее время.
Виды проездных документов Заключение договора перевозки между пассажиром и перевозчиком удостоверяется проездным документом (билетом).
Мир в начале XX века Мир в начале XX в. Страны мира к началу XX в. различались не только по своему положению в качестве метрополий .
Источник
Площадь поперечного сечения
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a 2 + b 2 = c 2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a 2 + b 2 )
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
где 2а – значение хорды, расчета площади поперечного сечения.
Источник
Поскольку
площади поперечных сечений стержня на
разных его участках различны, найдем
минимально необходимое значение
из условия прочности каждого из участков.
1. На первом
участке
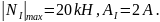
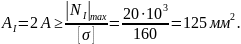
Отсюда получим
.
2. На втором участке
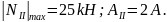
.
Отсюда следует,
что
.
3. На
третьем участке
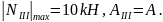
.
Из полученных
значений A
выбираем наибольшее, т.е. принимаем
.
В итоге получим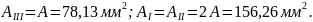
4. Построение эпюры нормальных напряжений
Построим эпюру
нормальных напряжений (т.е. график
),
которая позволит проверить правильность
подбора площадей поперечных сечений
стержня.
Нормальные
напряжения в сечении стержня определяем
по формуле (2.1).
Используя эту
формулу, установим закономерности
изменения напряжений на каждом из
участков
, (где i
номер участка).
I
участок
:

II
участок

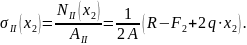
Отсюда следует:
при

при

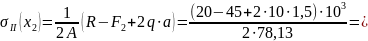
.
III
участок

.
Отсюда получим:
при


при

.
По полученным
данным строим эпюру
(см. рис. 6, в), порядок построения которой
аналогичен построению эпюры нормальных
сил N(x).
Анализ построенной
эпюры нормальных напряжений показывает,
что лишь в одном, наиболее нагруженном
сечении стержня напряжения достигают
допускаемой величины, а в других
поперечных сечениях напряжения меньше
допускаемых. Это свидетельствует о
правильности подбора площадей поперечных
сечений стержня.
5. Проверка выполнения условия жесткости
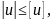
где
– осевое перемещение крайнего правого
сечения стержня.
Согласно (2.10)
.
Используя формулы
(2.8) или (2.9), определим абсолютные
удлинения (укорочения) участков стержня.
I
участок:

Поскольку
,
то используя формулу (2.9) получим
.
II
участок:
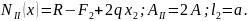
Согласно (2.8) находим
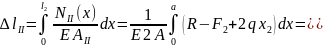

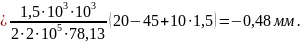
III
участок:
тогда
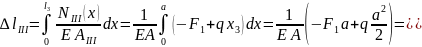
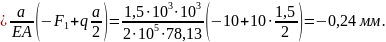
Перемещение
крайнего правого сечения стержня:

Проверяем выполнение
условия жесткости:

Требуемая
жесткость стержня обеспечена. Поэтому
в качестве окончательного принимаем
значение площади A,
установленное из условия прочности.
Примечание.
Если же условие жесткости не выполняется
и
превышает
более чем на 5 %, то значение площади A
определяют из условия жесткости. Для
этого записывают
в аналитическом виде и приравнивая к
,
находят необходимое значение площади
A.
Это значение будет больше того, что было
получено из условия прочности, и его
принимают в качестве окончательного.
2.6.2. Пример решения задачи №2.
Расчёт статически
неопределимой стержневой системы
Абсолютно жесткий
брус (рис. 7), нагруженный сосредоточенной
силой
,
опирается на шарнирно-неподвижную опору
и поддерживается стальными
шарнирно-закрепленными стержнями
круглого поперечного сечения.
Требуется:
Площади поперечных
сечений стержней
и
взять из расчета по допускаемым
напряжениям.
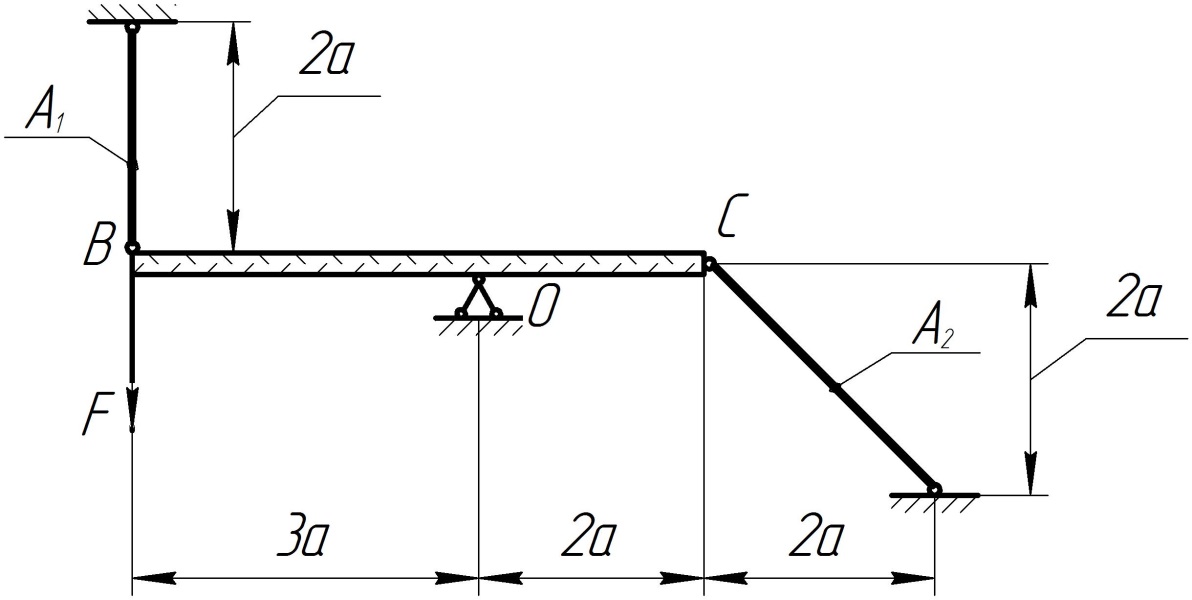
Рис. 7.
Статически неопределимая стержневая
система
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
You may encounter situations in which you have a three-dimensional solid shape and need to figure out the area of an imaginary plane inserted through the shape and having borders defined by the boundaries of the solid.
For example, if you had a cylindrical pipe running under your home measuring 20 meters (m) in length and 0.15 m across, you might want to know the cross-sectional area of the pipe.
Cross sections can be perpendicular to the orientation of the axes of the solid if any exist. In the case of a sphere, any cutting plane through the sphere regardless of orientation will result in a disk of some size.
The area of the cross-section depends on the shape of the solid determining the cross-section’s boundaries and the angle between the solid’s axis of symmetry (if any) and the plane that creates the cross section.
Cross-Sectional Area of a Rectangular Solid
The volume of any rectangular solid, including a cube, is the area of its base (length times width) multiplied by its height: V = l × w × h.
Therefore, if a cross section is parallel to the top or bottom of the solid, the area of the cross-section is l × w. If the cutting plane is parallel to one of the two sets the sides, the cross-sectional area is instead given by l × h or w × h.
If the cross-section is not perpendicular to any axis of symmetry, the shape created may be a triangle (if placed through a corner of the solid) or even a hexagon.
Example: Calculate the cross-sectional area of a plane perpendicular to the base of a cube with a volume of 27 m3.
-
Since l = w = h for a cube, any one edge of the cube must be 3 m long (since 3
× 3
× 3 = 27). A cross-section of the type described would therefore be a square 3 m on a side, giving an area of 9 m2.
Cross-Sectional Area of a Cylinder
A cylinder is a solid created by extending a circle through space perpendicular to its diameter. The area of a circle is given by the formula πr2, where r is the radius. It therefore makes sense that the volume of a cylinder would be the area of one of the circles forming its base.
If the cross-section is parallel to the axis of symmetry, then the area of the cross-section is simply a circle with an area of πr2. If the cutting plane is inserted at a different angle, the shape generated is an ellipse. The area uses the corresponding formula: πab (where a is the longest distance from the center of the ellipse to the edge, and b is the shortest).
Example: What is the cross-sectional area of the pipe under your home described in the introduction?
-
This is just πr2 = π(0.15 m)2=
π(0.0225) m2 = 0.071 m2. Note that the length of the pipe is irrelevant to this calculation.
Cross-Sectional Area of a Sphere
Any theoretical plane placed through a sphere will result in a circle (think about this for a few moments). If you know either the diameter or the circumference of the circle the cross-section forms, you can use the relationships C = 2πr and A = πr2 to obtain a solution.
Example: A plane is rudely inserted through the Earth very close to the North Pole, removing a section of the planet 10 m around. What is the cross-sectional area of this chilly slice of Earth?
- Since C = 2πr = 10 m, r = 10/2π = 1.59 m; A = πr2= π(1.59)2= 7.96 m2.
Площадь поперечного сечения
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
S = πR2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a2 + b2 = c2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a2 + b2)
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S= c*h
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
S=a*b
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
S =2R*h
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
S =2а*h
где 2а – значение хорды, расчета площади поперечного сечения.
Как определить площадь поперечного сечения
Если поперечное сечение объекта имеет сложную форму, для вычисления его площади следует разбить его на участки простых форм. После этого появится возможность рассчитать площади этих участков по соответствующим формулам, а затем их сложить.

Инструкция
Разделите поперечное сечение объекта на области, имеющие формы треугольников, прямоугольников, квадратов, секторов, кругов, полукругов и четвертей кругов. Если в результате разделения будут получаться ромбы, разделите каждый из них на два треугольника, а если параллелограммы – на два треугольника и один прямоугольник. Измерьте размеры каждой из этих областей: стороны, радиусы. Все измерения осуществляйте в одинаковых единицах.
Прямоугольный треугольник можно представить в виде половины прямоугольника, разделенного надвое по диагонали. Для расчета площади такого треугольника умножьте друг на друга длины тех сторон, которые примыкают к прямому углу (они называются катетами), затем результат умножения поделите на два. Если же треугольник прямоугольным не является, для расчета его площади вначале проведите в нем из любого угла высоту. Он окажется разделенным на два разных треугольника, каждый из которых будет прямоугольным. Измерьте длины катетов каждого из них, а затем по результатам измерений вычислите их площади.
Чтобы вычислить площадь прямоугольника, умножьте друг на друга длины двух его примыкающих друг к другу сторон. У квадрата они равны, поэтому можно длину одной стороны умножить саму на себя, то есть, возвести ее в квадрат.
Для определения площади круга поделите возведите его радиус в квадрат, а затем умножьте результат на число π. В случае, если фигура является не кругом, а полукругом, разделите площадь на два, а если четвертью круга – на четыре. У сектора измерьте угол между центром воображаемого центра и концами дуги, переведите его из градусов в радианы, умножьте на квадрат радиуса, а затем поделите на два.
Сложите все полученные площади между собой, и получится площадь, выраженная в единицах того же порядка, что и исходные данные. Например, если длины сторон и радиусы измерялись вами в миллиметрах, площадь получится в квадратных миллиметрах.
Значительно облегчить измерение площади сложной фигуры поможет прибор, называемый планиметром. Установите его шкалу на нуль, после чего проведите щупом по контуру фигуры. Прочитайте показания шкалы. Точность такого измерения получится сравнительно небольшой.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.