
Помогите ,пожалуйста, завтра контрольная, а я не знаю!!!
1) Как найти площадь поршня гидравлического пресса, если известна сила, которая давит на него, площадь второго поршня и сила, которая давит на второй поршень.
2) Как найти силу, которая давит на первый поршень, если известна площадь этого поршня, площадь второго поршня и сила, давящая на второй поршень.
(Если возникнут вопросы, то задавайте) Ответ запишите формулами и словами.
PLEASE, очень надо!!!
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,912 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Сообщающиеся сосуды. Гидравлический пресс
- Закон сообщающихся сосудов
- Сообщающиеся сосуды с различными жидкостями
- Гидравлический пресс
- Задачи
п.1. Закон сообщающихся сосудов
Как было показано в §31 данного справочника, давление столба жидкости не зависит от формы или размера дна сосуда. На одном и том же уровне (h) давление будет одинаковым.
Поэтому, когда жидкость приходит в равновесие, давление выравнивается, и её поверхность становится горизонтальной.
Второй случай с U-образной трубкой представляет значительный практический интерес, поскольку её колена являются так называемыми сообщающимися сосудами.
Сообщающиеся сосуды – сосуды с общим дном, в которых жидкость может свободно перетекать из одного колена в другое.
 |
Из сказанного выше следует, что при любой форме сообщающихся сосудов жидкость, налитая в них, будет перетекать, пока не установится на одном уровне в каждом из колен. |
Закон сообщающихся сосудов
В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне.
п.2. Сообщающиеся сосуды с различными жидкостями
Теперь рассмотрим, какой уровень установится, если в U-образную трубку налить две несмешивающиеся жидкости с различной плотностью, например, керосин и воду.
 |
На рисунке пунктиром обозначен горизонтальный уровень, который проходит под слоем керосина. На этом уровне в обоих коленах трубки находится вода, а значит, давления по закону Паскаля одинаковы. Можем записать $$ rho_2gh_2=rho_1gh_1 Rightarrow frac{h_2}{h_1}=frac{rho_1}{rho_2} $$ Получаем
|
В сообщающихся сосудах с различными жидкостями уровень жидкости выше в сосуде, в котором находится жидкость с меньшей плотностью.
п.3. Гидравлический пресс
Закон Паскаля и закон сообщающихся сосудов позволяет создавать гидравлические механизмы с многократным выигрышем в силе.
Гидравлический пресс состоит из двух сообщающихся цилиндрических сосудов разного диаметра. Сосуды заполняются водой, маслом или другой жидкостью. По закону Паскаля давление одинаково по всем направлениям и передается по всему объему.

Если подействовать на меньший поршень слева силой (F_1), направленной вниз, под поршнем возникнет избыточное давление (p=frac{F_1}{S_1}). Это давление будет передаваться по всему объему в жидкости, и под большим поршнем справа получим (p=frac{F_2}{S_2}). На большой поршень будет действовать сила (F_2=pS_2=F_1frac{S_2}{S_1}), направленная вверх.
За счет разности площади поршней получаем выигрыш в силе $$ k=frac{F_2}{F_1}=frac{S_2}{S_1} $$
Отношение силы давления большого поршня к силе давления малого поршня равно отношению площади большого поршня к площади малого поршня.
Гидравлический пресс был изобретен в 1795 году и с тех пор нашёл множество применений в различных отраслях производства. В современных прессах можно получить силу порядка сотен миллионов ньютонов, что используется для штамповки изделий из металла, прессования картона и хлопка, выдавливания масла из семян и т.д.
п.4. Задачи
Задача 1. Диаметр одного цилиндрического ведра в 1,2 раза больше, чем другого. В оба ведра налили по 5 л воды. В каком ведре давление на дно больше и во сколько раз?
Дано:
(d_1=1,2=d_2)
(V=5 text{л})
__________________
(frac{p_2}{p_1}-?)
Площадь дна каждого из ведер $$ S_1=frac{pi d^2_1}{4}, S_2=frac{pi d^2_2}{4} $$ Найдем высоту столба воды в каждом из ведер $$ V=ShRightarrow h_1=frac{V}{S_1}=frac{4V}{pi d^2_1}, h_2=frac{4V}{pi d^2_2} $$ Давление на дно в каждом из ведер $$ p_1rho gh_1=rho gcdotfrac{4V}{pi d^2_1}, p_2rho gh_2=rho gcdotfrac{4V}{pi d^2_2} $$ Отношение давлений $$ frac{p_2}{p_1}=frac{rho gcdot frac{4V}{pi d^2_2}}{rho gcdot frac{4V}{pi d^2_1}}=frac{d^2_1}{d^2_2}=left(frac{d_1}{d_2}right)^2 $$ Давление больше в узком ведре.
Отношение давлений равно отношению квадратов диаметров. $$ frac{p_2}{p_1}=1,2^2=1,44 $$ Ответ: больше в узком ведре; в 1,44 раза
Задача 2. Горизонтально расположенная труба заполнена водой и имеет два поршня. Площади поршней (S_1=10 text{см}^2, S_2=1 text{дм}^2). На поршень (B) действует сила (10 text{кН}). С какой силой нужно действовать на поршень (A), чтобы уравновесить силу, действующую на поршень (B)?
Дано:
(S_1=10 text{см}^2=0,001 text{м}^2)
(S_2=1 text{дм}^2=0,01 text{м}^2)
(F_2=10 text{кН}=10^4 text{Н})
__________________
(F_1-?)
При действии силы (F_2) на поршень (B) в воде возникает давление $$ p=frac{F_2}{S_2}. $$ По закону Паскаля давление передается во все стороны, и у поршня (A) получаем $$ p=frac{F_1}{S_1}. $$ Для уравновешивающей силы $$ frac{F_1}{S_1}=frac{F_2}{S_2}Rightarrow F-1=F_2frac{S_1}{S_2} $$ Подставляем $$ F_1=10^4cdot frac{0,001}{0,01}=10^3 (text{Н})=1 (text{кН}) $$ Ответ: 1 кН
Задача 3. U-образную трубку частично заполнили водой. В левое колено долили слой керосина высотой 25 см. В каком колене установился уровень выше? Найдите перепад высот (h) между уровнями поверхности воды в правом колене и уровнем керосина в левом колене. Ответ запишите в сантиметрах.
Дано:
(h_2=25 text{см}=0,25 text{м})
(rho_1=1000 text{кг/м}^3)
(rho_2=800 text{кг/м}^3)
__________________
(h-?)
На уровне под слоем керосина в обоих коленах трубки находится вода, а значит, давления на этом уровне по закону Паскаля одинаковы в обоих коленах. Можем записать $$ rho_2gh_2=rho_1gh_1Rightarrow h_1=frac{rho_2}{rho_1}h_2 $$ Поскольку плотность керосина меньше, уровень в левом колене с керосином выше.
Разность уровней begin{gather*} h=h_2-h_1=h_2-frac{rho_2}{rho_1}h_2\[7pt] h=left(1-frac{rho_2}{rho_1}right)h_2 end{gather*} Получаем: $$ h=left(1-frac{800}{1000}right)cdot 0,25=0,05 (text{м})=5 (text{см}) $$ Ответ: в левом колене с керосином; 5 см
Задача 4*. На дно мензурки налита ртуть и в нее опущен конец стеклянной трубки, запаянной сверху. Поверх ртути в мензурку налили слой воды высотой 25 см.
На какую высоту поднимется ртуть в стеклянной трубке?
Примите для расчетов (p_text{атм}=1,013cdot 10^5 text{Па}, g=9,8 text{м/с}^2)
Ответ укажите в миллиметрах.
На какую высоту поднимется ртуть при тех же условиях, если трубка не запаяна сверху?
Дано:
(rho_1=1000 text{кг/м}^3)
(rho_2=13600 text{кг/м}^3)
(h_1=25 text{см}=0,25 text{м})
(gapprox 9,8 text{м/с}^2)
(p_text{атм}=1,013cdot 10^5 text{Па})
__________________
(h_2-?, h’_2-?)
Рассмотрим запаянную трубку. На поверхность ртути, в которую опущен конец трубки, оказывают давление столб воды и атмосфера: $$ p=p_1+p_text{атм}=rho_1gh_1+p_text{атм} $$ Под действием этого давления ртуть в запаянной трубке поднимется на высоту $$ h_2=frac{p}{rho_2g}=frac{rho_1gh_1+p_text{атм}}{rho_2g} $$ Получаем $$ h_2=frac{1000cdot 9,8cdot 0,25+1,013cdot 10^5}{13600cdot 9,8}approx 0,778 (text{м})=778 (text{мм}) $$ Если трубка будет не запаяна, то при подъеме в ней ртути на нее сверху будет действовать атмосферное давление. Высота подъема begin{gather*} h’_2=frac{p-p_text{атм}}{rho_2g}=frac{rho_1gh_1}{rho_2g}=frac{rho_1}{rho_2}h_1\[7pt] h’_2=frac{1000}{13600}cdot 0,25approx 0,018 (text{м})=18 (text{мм}) end{gather*} Ответ: 778 мм; 18 мм
Примечание: заметим, что разность (h_text{атм}=778-18 = 760 text{мм}) – это нормальное атмосферное давление, измеренное в «миллиметрах ртутного столба» (см. §31 данного справочника). Поэтому (h_2=h’_2+h_text{атм}).
Задача 5. Малый поршень гидравлического пресса под действием силы 500 Н опустился на 9 см. При этом большой поршень поднялся на 3 см.
Какая сила действует на большой поршень со стороны жидкости?
Дано:
(F_1=500 text{Н})
(h_1=9 text{см}=0,09 text{м})
(h_2=3 text{см}=0,03 text{м})
__________________
(F_2-?)
Объем воды, вытесняемый при движении малого поршня вниз: (V=h_1S_1).
Жидкости практически несжимаемы, поэтому этот объем должен «прирасти» в цилиндре большого поршня за счет его движения вверх: (V=h_2S_2).
Получаем для выигрыша в силе: $$ h_1S_1=h_2S_2Rightarrow frac{S_2}{S_1}=frac{h_1}{h_2} $$ Выигрыш в силе равен отношению длин хода малого и большого поршней.
Выигрывая в силе, мы проигрываем в расстоянии.
Сила, действующая на большой поршень: $$ F_2=F_1frac{S_2}{S_1}=F_1frac{h_1}{h_2} $$ Подставляем: $$ F_2=500cdot frac{0,09}{0,03}=1500 (text{Н})=1,5 (text{кН}) $$ Ответ: 1,5 кН
Задача 6. Малый поршень гидравлического пресса площадью 1 м2 под действием силы 2 кН опустился на 24 см. Площадь большего поршня 8 м2. Найдите вес груза, который был поднят большим поршнем и высоту, на которую он был поднят.
Дано:
(S_1=1 text{м}^2)
(F_1=2000 text{Н})
(h_1=24 text{см}=0,24 text{м})
(S_2=8 text{м}^2)
__________________
(P-?, h_2-?)
Вес груза, который можно поднять с помощью пресса, равен силе (F_2), которая действует на большой поршень: $$ P=F_2=F_1frac{S_2}{S_1} $$ Получаем $$ P=2000cdot frac 81=16000 (text{Н})=16 (text{кН}) $$ Объем воды, вытесняемый при движении малого поршня вниз: (V=h_1S_1).
Жидкости практически несжимаемы, поэтому этот объем должен «прирасти» в цилиндре большого поршня за счет его движения вверх: (V=h_2S_2).
Следовательно $$ h_1S_1=h_2S_2Rightarrow h_2=h_1frac{S_1}{S_2} $$ Получаем begin{gather*} h_2=0,24cdot frac 81=0,03 (text{м})=3 (text{см}) end{gather*} Ответ: 16 кН; 3 см
Задача 7*. На дне аквариума лежал камень массой 390 г, полностью погруженный в воду. Когда его убрали, давление воды на дно аквариума уменьшилось на 25 Па. Найдите плотность камня, если длина аквариума 40 см, а ширина 14 см. ((g=9,8 text{м/с}^2)).
Дано:
(m=390 text{г}=0,39 text{кг})
(Delta p=25 text{Па})
(a=40 text{см}=0,4 text{м})
(b=14 text{см}=0,14 text{м})
(rho_0=1000 text{кг/м}^3)
(g=9,8 text{м/с}^2)
__________________
(rho-?)
Лежа на дне, камень занимал в аквариуме некий объем $$ V_text{к}=frac{m}{rho} $$ Остальной объем занимала вода. Их суммарный объем $$ V=V_text{в}+V_text{к}=Sh=abh $$ Высота слоя воды в аквариуме с камнем $$ h_1=frac{V_text{в}+V_text{к}}{ab} $$ Давление воды на дно в аквариуме с камнем begin{gather*} p_1=rho_0gh_1= rho_0gfrac{V_text{в}+V_text{к}}{ab} end{gather*} Когда камень забрали, в аквариуме осталась только вода объемом (V_text{в}).
Высота слоя воды в аквариуме без камня $$ h_2=frac{V_text{в}}{ab} $$ Давление воды на дно в аквариуме без камня $$ p_2=rho_0gh_2=rho_0gfrac{V_text{в}}{ab} $$ Разность давлений $$ Delta p=p_1-p_2=rho_0 gfrac{V_text{в}+V_text{к}}{ab}-rho_0gfrac{V_text{в}}{ab}=rho_0gfrac{V_text{к}}{ab}=frac{rho_0g}{ab}cdot frac{m}{rho} $$ Откуда плотность камня $$ rho=frac{rho_0g}{ab}cdot frac{m}{Delta p} $$ Подставляем $$ rho=frac{1000cdot 9,8}{0,4cdot 0,14}cdotfrac{0,39}{25}=2730 (text{кг/м}^3) $$ Ответ: 2730 кг/м3
Содержание:
- § 1 Гидравлическая машина
- § 2 Гидравлический пресс
- § 3 Решение задач
- § 4 Важно запомнить
§ 1 Гидравлическая машина
В этом уроке мы изучим устройство и принцип действия гидравлических машин.
В жизни человеку очень часто приходится сталкиваться с такими ситуациями, где нужно поднять груз большой массы на высоту или сжать какое-либо тело. Например, автомобилисту нужно сменить проколотое колесо. Для этого нужно приподнять автомобиль. Поднять 5 кг, 10 кг взрослому человеку не так сложно. Но поднять автомобиль? Или нужно выжать масло из семян подсолнуха, спрессовать бумагу. И вот в таких случаях на помощь приходят разные механизмы, позволяющие получить большую силу, прилагая незначительные усилия.
Одним из таких механизмов является гидравлическая машина.
Гидравлическая машина (от греческого слова гидравликос – водяной) – это машина, действие которой основано на законах движения и равновесия жидкостей. Первая гидравлическая машина была создана Паскалем, который называл ее машиной для увеличения силы.
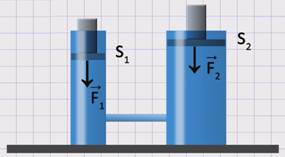
Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью (водой или маслом).
Рассмотрим принцип действия гидравлической машины. Обозначим площадь поршня в малом цилиндре S1, площадь поршня в большом цилиндре – S2, F1 и F2 – силы, действующие на поршни.
Если на поршень S1 подействовать с силой F1, то давление в малом цилиндре будет определяться по формуле:
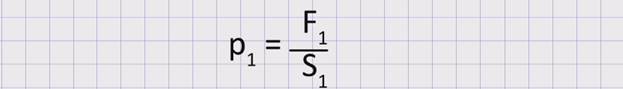
Давление в большом цилиндре:
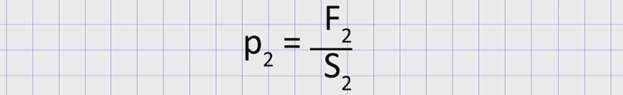
По закону Паскаля давление, производимое на жидкость или газ, передается в каждую точку по всем направлениям одинаково. Значит, давление в обоих цилиндрах будет одинаковым: p1 = p2 . Тогда можем приравнять правые части этих формул:

Читается эта формула так: сила F2, действующая на большой поршень, во столько раз больше силы F1, действующей на малый поршень, во сколько раз площадь большого поршня S2 больше площади малого поршняS1. Отношение F2 к F1показывается выигрышем в силе.
Итак, сделаем вывод. Приложив незначительное усилие F1 к малому поршню, мы можем получить во столько раз большую силу F2 на большом поршне, во сколько раз его площадь превышает площадь малого поршня.
Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.
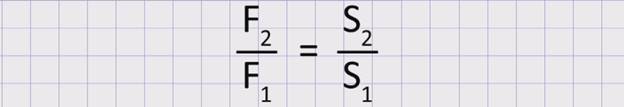
§ 2 Гидравлический пресс
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.
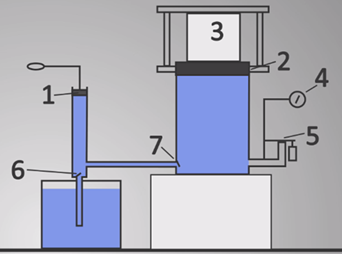
Принцип действия гидравлического пресса таков: на платформу большого поршня 2 кладется прессуемое тело 3. При помощи малого поршня 1 создается давление на жидкость, которое по закону Паскаля передается в каждую точку жидкости, заполняющей цилиндры. Так как площадь большого поршня во много раз больше площади малого, то и действующая на него сила окажется во столько же раз больше. Под действием этой силы большой поршень поднимается и сжимает тело. За значением давления, возникающего в жидкости, следят при помощи деформационного манометра 4, соединенного с предохранительным клапаном 5, который автоматически открывается при превышении допустимого значения давления. Клапаны 6 и 7 служат для перекачивания жидкости: при подъеме малого поршня 1 открывается клапан 6, и жидкость поступает в малый сосуд; при нажатии давление увеличивается, и этот клапан закрывается; открывается клапан 7, и жидкость переходит в большой сосуд.
Гидравлические прессы применяются для выжимания масла на маслобойных заводах, для прессования фанеры, картона, сена. В автомобилях используется гидравлический тормоз, в мастерских и в быту применяют гидравлический домкрат.
§ 3 Решение задач
Рассмотрим решение задачи на расчет выигрыша в силе в гидравлических машинах.

Запишем условие задачи. Нам известны масса m= 1500 кг, площадь малого поршня S1 = 10 см2 = 0, 001 м2, площадь большого поршня S2 = 0,1 м2. Найти F1.
Решение: Запишем формулу выигрыша в силе при помощи гидравлической машины:

Ответ: сила, приложенная к малому поршню,150 Н

Запишем условие задачи: F1= 200 Н, p = 400000 Па, S2 =0,04 м2. Найти показания динамометра, т.е. силу F2 = ? S1 =?

Ответ:F2 = 16 000 Н, S1 = 5 см2
§ 4 Важно запомнить
Гидравлическая машина – это машина, действие которой основано на законе Паскаля.
Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью.
Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.
Гидравлические прессы применяются для выжимания масла, для прессования фанеры, картона, сена. В автомашинах используется гидравлический тормоз, для подъема груза предназначен гидравлический домкрат.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. – М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября», 2002. – 272 с.
Использованные изображения:
«Важный вопрос, который следует задавать,
приступая к работе, это не вопрос
«Что я получу?»; вместо этого Вы должны
спрашивать себя «Каким я стану?»
Д. Рон
Данная тема будет связана с решением задач на тему «Закон
Паскаля. Гидравлический пресс».
Задача 1. Поршень гидравлического пресса, площадь
сечения которого составляет 200 см2, действует на зажатое в нем тело
силой 20 кН. Определите силу, с которой действует меньший поршень на масло в
прессе, если его площадь сечения 5 см2.
|
ДАНО: |
СИ |
РЕШЕНИЕ: Соотношение сил в гидравлическом прессе: Откуда искомая сила равна |
|
|
Ответ: 500 Н.
Задача 2. Малый поршень гидравлического пресса за один
ход опускается на расстояние 0,2 м, а большой поршень поднимается на 0,01 м. С
какой силой действует пресс на зажатое в нем тело, если на малый поршень
действует сила 500 Н?
|
ДАНО: |
РЕШЕНИЕ: Сила, действующая на малый поршень пресса, создает Сила, действующая на большой поршень: Запишем условие несжимаемости жидкости Согласно закону Паскаля, жидкость передает производимое на Тогда искомая сила |
|
|
Ответ: 10 кН.
Задача 3. Поршни гидравлического пресса, заполненного
водой, находятся на одном уровне. Если на большой поршень площадью 0,1 м2
встанет человек массой 70 кг, то поршень опуститься на 3 см. На какую высоту
при этом поднимется малый поршень, площадь которого 35 см2? Массы
поршней 700 г и 2 кг соответственно.
|
ДАНО: |
СИ |
РЕШЕНИЕ: Давление, которое создает малый поршень, было уравновешено Давление, создаваемое малым поршнем: Давление, создаваемое большим поршнем: Давление, создаваемое человеком: Давление столба воды: По закону Паскаля: Подставляя в закон Паскаля выражения, записанные выше, Преобразуем данную формулу и выразим из неё искомую высоту |
|
|
Ответ: 49 см.
Задача 4. Гидравлический пресс, заполненный водой,
имеет поршни, площади которых 200 см2 и 20 см2. На
большой поршень положили груз массой 60 кг. На какую высоту поднимется после
этого малый поршень? Плотность воды примете равной 1000 кг/м3.
|
ДАНО: |
РЕШЕНИЕ: В данной задаче ничего не говорится о том, с какими Допустим, что в отсутствии груза малый поршень пресса При равновесии жидкости, давление в точках, принадлежащих Давление в точке А: Давление в точке B: Тогда получаем В результате воздействия груза на большой поршень, малый Давление в точке А1: Давление в точке B1: Теперь запишем для этого состояния условие равновесия как Таким образом, получаем систему уравнений Решим систему уравнений методом подстановки Запишем условие несжимаемости жидкости Тогда получим Тогда искомая величина равна |
Ответ: 2,7 м.
Задача 5. С помощью гидравлического пресса с КПД 75%
требуется спрессовать тело массой 80 т так, чтобы максимальная сила давления на
верхнюю площадку пресса достигала величины 1 МН. Считая, что деформация тела по
вертикали подчиняется закону Гука, а тело при этом сжимается на 0,3 м, найти
величину работы, совершенной двигателем. Отношение площадей поршней 1/50.
Определите число ходов малого поршня, если за один ход он опускается на 0,1 м.
|
ДАНО: |
СИ |
РЕШЕНИЕ: Работа переменной силы давления второго поршня на тело Минимальная сила давления большого поршня на тело: Максимальная сила давления большого поршня на тело: Тогда работа равна Коэффициент полезного действия любого механизма Выразим совершенную работу прессом Запишем условие несжимаемости жидкости Объем жидкости, вытесненной малым поршнем: Объем жидкости, поступившей в широкий сосуд: Приравняем последние два выражения и далее выразим искомое |
|
|
Ответ: A1 = 513600 Дж; n = 150.
