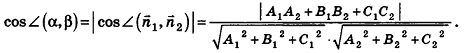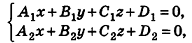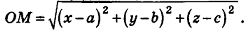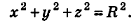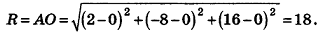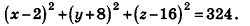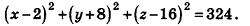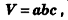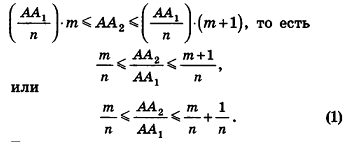Загрузить PDF
Загрузить PDF
Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру. Площадь поверхности является числовой характеристикой поверхности.[1]
Вычислить площадь поверхности объемной (трехмерной) фигуры довольно просто, если знать соответствующую формулу. Существует определенная формула для каждой фигуры, поэтому сначала нужно определить, какая фигура дана. Чтобы быстро вычислять площадь поверхности, запомните соответствующие формулы для разных фигур. В данной статье рассматриваются наиболее распространенные фигуры.
-
1
Запишите формулу для вычисления площади поверхности куба. У куба шесть равных квадратных граней. Так как стороны квадрата равны, площадь квадрата равна a2, где а – сторона. Так как у куба шесть равных квадратных граней, чтобы найти площадь поверхности, умножьте площадь одной грани (квадрата) на 6. Формула для вычисления площади поверхности (SA) куба: SA = 6а2, где а – ребро куба (сторона квадрата).[2]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте ребро куба. Ребра куба равны, поэтому можно измерить только одно (любое) ребро. Ребро измерьте с помощью линейки (или рулетки). Обратите внимание на используемые единицы измерения.
- Запишите значение, обозначив его через а.
- Например: а = 2 см
-
3
Значение а возведите в квадрат. То есть возведите в квадрат длину ребра куба. Для этого умножьте значение на себя. Если вы только приступили к изучению формул с квадратами, запишите формулу так: SA = 6*а*а.
- Сейчас вы вычислили значение площади одной из граней куба.
- Например: а = 2 см
- a2 = 2 х 2 = 4 см2
-
4
Вычисленное значение умножьте на шесть. Помните, что у куба шесть равных граней. Вычислив площадь одной из граней, умножьте полученное значение на 6, чтобы включить все грани куба.
- Это последний шаг в процессе вычисления площади поверхности куба.
- Например: а 2 = 4 см2
- SA = 6 х а2 = 6 х 4 = 24 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности прямоугольной призмы. У прямоугольной призмы шесть граней, причем равными являются только противоположные грани.[3]
Поэтому формула для вычисления площади поверхности прямоугольной призмы включает значения трех разных ребер: SA = 2ab + 2bc + 2ac.- Здесь а – ширина, b – высота, с – длина призмы.
- Если проанализировать формулу, можно понять, что она суммирует площади всех граней.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Найдите значения высоты, ширины и длины призмы. Три ребра не являются равными, поэтому нужно выполнить три измерения. Измерьте соответствующие ребра с помощью линейки (или рулетки). Ребра измеряйте в одной единице измерения.
- Измерьте длину грани, которая лежит в основании призмы; длину обозначьте через с.
- Например: с = 5 см
- Измерьте ширину грани, которая лежит в основании призмы; ширину обозначьте через а.
- Например: а = 2 см
- Измерьте высоту призмы; высоту обозначьте через b.
- Например: b = 3 см
-
3
Вычислите площадь одной грани призмы, а затем полученное значение умножьте на два. Помните, что у прямоугольной призмы шесть граней, причем равными являются только противоположные грани. Умножьте длину на высоту (с на а), чтобы найти площадь одной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[4]
- Например: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 см2
-
4
Вычислите площадь другой грани призмы, а затем полученное значение умножьте на два. Умножьте ширину на высоту (а на b), чтобы найти площадь другой грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[5]
- Например: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 см2
-
5
Вычислите площадь фронтальной грани, а затем полученное значение умножьте на два. Умножьте длину на ширину (с на b), чтобы найти площадь фронтальной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[6]
- Например: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 см2
-
6
Сложите три значения. Так как площадь поверхности – это суммарная площадь всех граней фигуры, сложите найденные значения площадей отдельных граней. Вы получите площадь поверхности прямоугольной призмы.[7]
- Например: SA = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности треугольной призмы. Треугольная призма имеет две равные треугольные грани и три прямоугольные грани. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти площади всех граней и сложить их. Формула для вычисления площади поверхности треугольной призмы: SA = 2S + РH, где S – площадь треугольной грани, Р – периметр треугольной грани, H – высота призмы.[8]
- Здесь S – это площадь треугольника (треугольной грани), которая вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание).
- Р – периметр треугольника (треугольной грани), который равен сумме всех сторон треугольника.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Вычислите площадь треугольной грани и умножьте ее на два. Площадь треугольника вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание). Так как треугольная призма имеет две равные треугольные грани, эту формулу можно умножить на два. Поэтому, чтобы вычислить площади двух треугольных граней, просто перемножьте основание и высоту треугольника (b*h).[9]
- Основание треугольника b – это его нижняя сторона.
- Например: b = 4 см
- Высота треугольника h – это перпендикуляр, опущенный на основание из противоположной вершины.
- Например: h = 3 см
- Площадь двух треугольных граней равна: 2(1/2)b*h = b*h = 4*3 =12 см.
-
3
Измерьте каждую сторону треугольника и высоту призмы. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти значение каждой стороны треугольника и высоты призмы. Высота призмы – это расстояние между треугольными гранями.
- Например: Н = 5 см
- Стороны треугольника – это три ребра одной (любой) из треугольных граней.
- Например: а = 2 см, b = 4 см, с = 6 см
-
4
Вычислите периметр треугольника. Для этого сложите все стороны треугольника: Р = а + b + с.
- Например: P = а + b + с = 2 + 4 + 6 = 12 см
-
5
Перемножьте периметр треугольной грани и высоту призмы. Помните, что высота призмы – это расстояние между треугольными гранями. Таким образом, Р умножьте на Н.
- Например: Р х Н = 12 х 5 = 60 см2
-
6
Сложите полученные значения. Чтобы найти площадь поверхности треугольной призмы, сложите два значения, вычисленные ранее.[10]
- Например: 2S + PH = 12 + 60 = 72 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности шара. Шар имеет изогнутую поверхность, поэтому формула включает математическую константу π (число Пи). Чтобы вычислить площадь поверхности шара, воспользуйтесь формулой SA = 4π*r2.[11]
- Здесь r – радиус шара, π ≈ 3,14.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус шара. Радиус шара равен половине его диаметра, то есть половине отрезка, который проходит через центр шара и соединяет две точки, лежащие на его поверхности.[12]
- Например: r = 3 см
-
3
Радиус шара возведите в квадрат. Для этого умножьте значение радиуса (r) на себя. Помните, что формулу можно записать так: SA = 4π*r*r.[13]
- Например: r2 = r x r = 3 x 3 = 9 см2
-
4
Перемножьте квадрат радиуса и приблизительное значение числа Пи. Число Пи является математической константой, которая равна отношению длины окружности к ее диаметру.[14]
Это иррациональное число со множеством цифр после десятичной запятой. Зачастую число Пи округляется до 3,14. Квадрат радиуса умножьте на π (на 3,14), чтобы вычислить площадь круглого сечения шара. [15]
- Например: π*r2 = 3,14 x 9 = 28,26 см2
-
5
Полученное значение умножьте на четыре. Чтобы найти значение площади поверхности сферы, площадь круглого сечения умножьте на 4.[16]
- Например: 4π*r2 = 4 x 28,26 = 113,04 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности цилиндра. Цилиндрическая поверхность этой фигуры ограничена двумя круглыми параллельными плоскостями, которые называются основаниями. Формула для вычисления площади поверхности цилиндра: SA = 2π*r2 + 2π*rh, где r – радиус основания, h – высота цилиндра, π ≈ 3,14.[17]
- 2π*г2 – это площадь двух оснований, а 2πrh – это площадь цилиндрической поверхности.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус основания и высоту цилиндра. Радиус окружности равен половине ее диаметра, то есть половине отрезка, который проходит через центр окружности и соединяет две точки, лежащие на ней.[18]
Высота цилиндра – это расстояние между его основаниями. Измерьте и запишите радиус основания и высоту цилиндра.- Например: r = 3 см
- Например: h = 5 см
-
3
Вычислите площадь основания и умножьте ее на два. Чтобы найти площадь основания, воспользуйтесь формулой для вычисления площади круга: S = π*г2. Сначала радиус возведите в квадрат, а затем полученное значение умножьте на число Пи. Результат умножьте на два, чтобы учесть второе равное основание.[19]
- Например: площадь основания = π*r2 = 3,14 х 3 х 3 = 28,26 см2
- Например: 2π*r2 = 2 x 28,26 = 56,52 см2
-
4
Вычислите площадь цилиндрической поверхности. Для этого воспользуйтесь формулой S = 2π*rh, по которой можно найти площадь поверхности трубы. Здесь труба – это поверхность между двумя основаниями цилиндра. Перемножьте двойку, число Пи, радиус и высоту.[20]
- Например: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 см2
-
5
Сложите полученные значения. Сложите площади двух оснований и площадь цилиндрической поверхности (между двумя основаниями), чтобы вычислить общую площадь поверхности цилиндра. Обратите внимание, что при сложении этих величин получится исходная формула: SA = 2π*r2 + 2π*rh.[21]
- Например: 2π*r2 + 2π*rh = 56,52 + 94,2 = 150,72 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности квадратной пирамиды. Квадратная пирамида имеет одно квадратное основание и четыре треугольные грани. Помните, что площадь квадрата равна квадрату его стороны. Площадь треугольника равна 1/2sl (половина основания треугольника, умноженная на его высоту). Так как пирамида имеет четыре треугольные грани, нужно площадь треугольника умножить на 4. Таким образом, площадь поверхности квадратной пирамиды вычисляется по формуле: SA = s2 + 2sl.[22]
- В этой формуле s – ребро квадратной грани (сторона квадрата), l – апофема пирамиды.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Найдите значения апофемы и ребра квадратной грани. Апофема (l) – это высота треугольной грани, то есть расстояние между основанием треугольника и его вершиной. Ребро квадратной грани (s) – это сторона квадрата. Помните, что у квадрата все стороны равны, поэтому измерьте любое ребро квадратной грани, а также измерьте апофему пирамиды.[23]
- Например: l = 3 см
- Например: s = 1 см
-
3
Найдите площадь квадратной грани. Для этого возведите в квадрат ребро этой грани (сторону квадрата), то есть умножьте значение s на себя.[24]
- Например: s2 = s х s = 1 х 1 = 1 см2
-
4
Вычислите общую площадь четырех треугольных граней. Вторая часть формулы включает суммарную площадь четырех треугольных граней. Согласно формуле 2ls, перемножьте 2, s и l. Так вы найдете суммарную площадь 4-х треугольных граней.[25]
- Например: 2 х s х l = 2 х 1 х 3 = 6 см2
-
5
Сложите полученные значения. Сложите площадь квадратной грани и общую площадь четырех треугольных граней, чтобы вычислить площадь поверхности пирамиды.[26]
- Например: s2 + 2sl = 1 + 6 = 7 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности конуса. Конус имеет круглое основание и закругленную боковую поверхность, которая сужается в вершине этой фигуры. Чтобы найти площадь поверхности конуса, нужно вычислить значения площади круглого основания и площади боковой поверхности, а затем сложить эти значения. Формула для вычисления площади поверхности конуса: SA = π*r2 + π*rl, где r – радиус круглого основания, l – образующая (расстояние между вершиной конуса и точкой, которая лежит на окружности круга), π ≈ 3,14.[27]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус основания и высоту конуса. Радиус – это отрезок, соединяющий центр круга и точку, которая лежит на его окружности. Высота – это расстояние между центром круга и высотой конуса.[28]
- Например: r = 2 см
- Например: h = 4 см
-
3
Найдите значение образующей конуса (l). Образующая конуса является гипотенузой треугольника, поэтому воспользуйтесь теоремой Пифагора, чтобы вычислить образующую: l = √(r2 + h2), где r – радиус круглого основания, h – высота конуса.[29]
- Например: l = √(r2 + h2) = √(2 х 2 + 4 х 4) = √(4 + 16) = √(20) = 4,47 см
-
4
Вычислите площадь круглого основания. Площадь круга вычисляется по формуле S = π*r2. Измерив радиус, возведите его в квадрат (умножьте r на себя), а затем квадрат радиуса умножьте на число Пи.[30]
- Например: π*r2 = 3,14 x 2 x 2 = 12,56 см2
-
5
Вычислите площадь боковой поверхности конуса. Сделайте это по формуле S = π*rl, где r – радиус круга, l – образующая, которая найдена ранее.[31]
- Например: π*rl = 3,14 x 2 x 4,47 = 28,07 см
-
6
Сложите полученные значения, чтобы найти площадь поверхности конуса. Площадь поверхности конуса равна сумме площади круглого основания и площади боковой поверхности конуса.[32]
- Например: π*r2 + π*rl = 12,56 + 28,07 = 40,63 см2
Реклама
Что вам понадобится
- Линейка
- Ручка или карандаш
- Бумага
Об этой статье
Эту страницу просматривали 69 399 раз.
Была ли эта статья полезной?
Площадь поверхности многогранника. В данной рубрике в опубликованных статьях ” Общий обзор. Формулы стереометрии ” и ” Что ещё необходимо знать для решения по стереометрии ” мы уже рассмотрели теоретические моменты, которые необходимы для решения.
В составе ЕГЭ по математике имеется целый ряд задач на определение площади поверхности и объема составных многогранников. Это, наверное, одни из самых простых задач по стереометрии. НО! Имеется нюанс. Не смотря на то, что сами вычисления просты, ошибку при решении такой задачи допустить очень легко.
В чём же дело? Далеко не все обладают хорошим пространственным мышлением, чтобы сразу увидеть все грани и параллелепипеды из которых «состоят» многогранники. Даже если вы умеете делать это очень хорошо, можете мысленно сделать такую разбивку, всё-таки следует не торопиться и воспользоваться рекомендациями из этой статьи.
Кстати, пока работал над данным материалом, нашёл ошибку в одной из задач на сайте. Нужна внимательность и ещё раз внимательность, вот так.
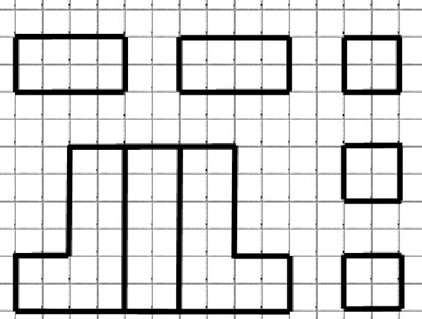
Итак, если стоит вопрос о площади поверхности, то на листе в клетку постройте все грани многогранника, обозначьте размеры. Далее внимательно вычисляйте сумму площадей всех полученных граней. Если будете предельно внимательны при построении и вычислении, то ошибка будет исключена.
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Используем оговоренный способ. Он нагляден. На листе в клетку строим все элементы (грани) в масштабе. Если длины рёбер будут большими, то просто подпишите их.
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ещё задачи 25881 , 77155 , 77156 . В них приведены решения другим способом (без построения), постарайтесь разобраться — что откуда взялось. Также решите уже представленным способом.
Если требуется найти объём составного многогранника. Разбиваем многогранник на составляющие его параллелепипеды, записываем внимательно длины их рёбер и вычисляем.
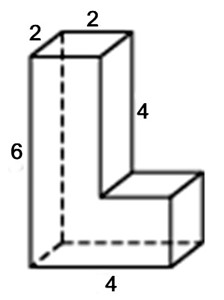
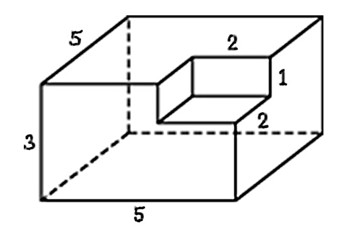
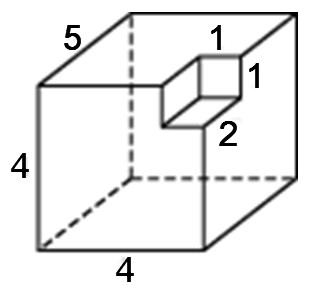
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Объем многогранника, изображенного на рисунке равен сумме объёмов двух многогранников с рёбрами 6,2,4 и 4,2,2
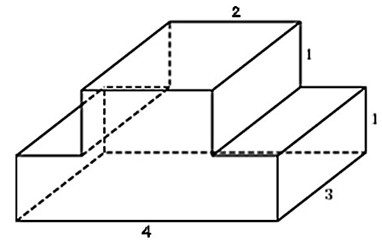
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
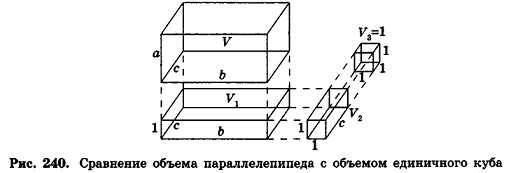
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
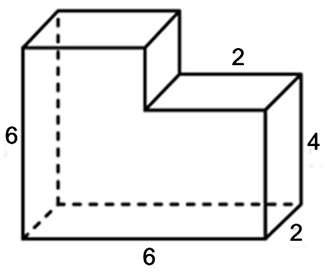
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Казалось бы, данные задачи можно вообще не рассматривать, они же просты и понятны. Но в их решении важна практика. Повторюсь, что ошибиться очень легко, попрактикуйтесь с подобными задачами и вы убедитесь.
В отк рытом банке задач много примеров аналогичных задач (смотрите здесь и здесь ). Договоритесь с одноклассниками решить одни и те же задачи, затем сверьтесь.
Мы продолжим рассматривать задачи данной части, не пропустите! Успехов вам.
Задание 8 (№ 25641) из Открытого банка заданий для подготовки к ЕГЭ по математике.
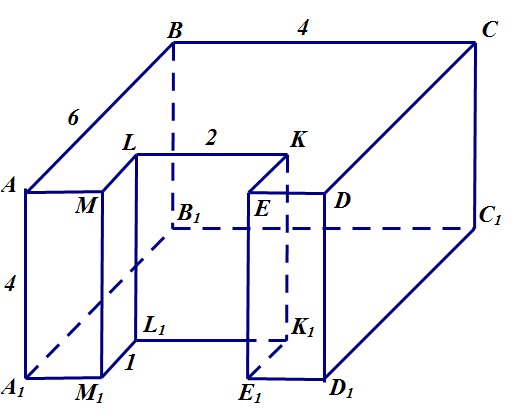
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)
Решение. Площадь поверхности многогранника равна сумме площадей всех его граней. Так как все грани этого многогранника — прямоугольники, то для нахождения площади каждой грани мы используем формулу площади прямоугольника:
S=ab, где a и b — длины двух смежных сторон прямоугольника.
Обозначим вершины многогранника:
1.Найдем сначала площадь боковой поверхности. Для этого, чтобы не пропустить ни одной грани, обойдем наш многогранник по часовой стрелке, и запишем площадь каждой грани:
2. Найдем площадь верхней грани. Для этого из площади прямоугольника ABCD вычтем площадь прямоугольника MLKE:
3. Площадь нижней грани равна площади верхней грани и равна 22.
4. Сложим получившиеся площади: 88+22+22=132.
Задание 8_1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности многогранника можно вычислить как сумму площадей всех его граней. Причем площади передней и задней граней, равны

и вся площадь поверхности равна
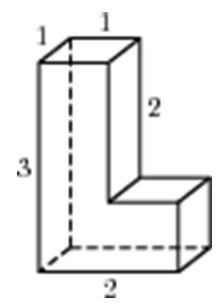
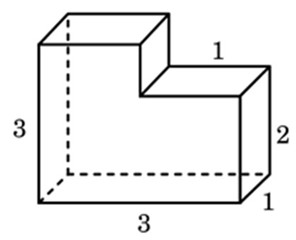
Задание 8_2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдем площадь поверхности как площадь поверхности прямоугольного параллелепипеда со сторонами 3, 3, 5 и вычтем площади двух граней 1х1 прямоугольного параллелепипеда со сторонами 1, 1 и 3 (см. рисунок).
Площадь поверхности большого параллелепипеда, равна

Площади двух граней 1х1 малого параллелепипеда, равны:

и площадь поверхности фигуры

Задание 8_3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Из рисунка видно, что площадь поверхности фигуры будет меньше площади прямоугольного параллелепипеда со сторонами 3, 4 и 5 на площади двух квадратов, размером 1х1, имеем:

Задание 8_4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Можно заметить, что площадь поверхности данной фигуры будет в точности совпадать с площадью поверхности прямоугольного параллелепипеда со сторонами 5, 3 и 5 и равна

Замечание. Не путайте вычисление объема фигуры и площади его поверхности!
Задание 8_5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности данной фигуры равна площади поверхности прямоугольного параллелепипеда со сторонами 3, 5 и 4, и равна

Замечание. Не путайте вычисление объема фигуры и площади его поверхности!
Задание 8_6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности данной фигуры можно вычислить как площадь поверхности прямоугольного параллелепипеда со сторонами 4, 4 и 6 плюс две грани 1х4 площадью 4 (см. рисунок) и минус две грани площадью 2х1 (они вычитаются из оснований). Таким образом, площадь фигуры равна

Задание 8_7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площади нижней и верхней граней равны 



Задание 8_8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности фигуры можно вычислить как площадь поверхности прямоугольного параллелепипеда со сторонами 4, 3 и 2, минус четыре площади боковых квадратов, размером 1х1. Имеем:

Задание 8_9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
На рисунке изображен прямоугольный параллелепипед с вырезом. Площадь поверхности такой фигуры будет равна площади поверхности всего параллелепипеда со сторонами 5, 7 и 1 минус две площади фронтального выреза площадью 2х1=2 и плюс четыре площади внутренних сторон выреза размерами 1х1 и 2х1. Таким образом, вся площадь поверхности многогранника равна
Задание 8_10. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности многогранника можно найти как сумму площадей двух прямоугольных параллелепипедов со сторонами 5, 4, 3 и 3, 2, 3 минус две площади основания нижнего параллелепипеда площадью 2х3 (две площади, т.к. она будет дважды учтена в большом и малом параллелепипедах). Таким образом, получаем:
Задание 8_11. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Найдем площадь поверхности фигуры как площадь прямоугольного параллелепипеда со сторонами 2, 2, 1 и вычтем две площади граней 1х1 во фронтальных плоскостях (передней и задней), получим:
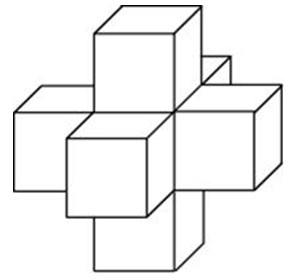
Задание 8_12. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Площадь поверхности данной фигуры можно найти как сумму площадей поверхности 6 кубов минус площадь поверхности одного куба (тот что внутри и эти грани не входят в площадь поверхности), получаем:
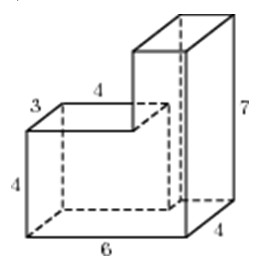
Задание 8_13. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдем площадь поверхности этого многогранника как сумму площадей поверхности большого (6х6х2) и малого (3х3х4) прямоугольных параллелепипедов и вычтем дважды площадь поверхности соприкосновения граней этих параллелепипедов, которая имеет размер 3х4, получим:
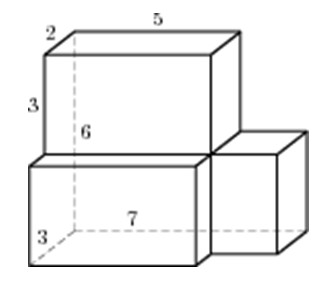
Задание 8_14. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности этого многогранника можно найти как сумму площадей поверхности каждого из трех параллелепипедов размерами 2х5х6, 2х5х3 и 2х3х2 минус удвоенные площади соприкосновения этих параллелепипедов, то есть минус удвоенные площади двух граней размерами 3х5 и 2х3 соответственно. В результате получаем площадь поверхности фигуры:
Задание 8_15. Через среднюю линию основания треугольной призмы, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности призмы, если площадь боковой поверхности отсеченной треугольной призмы равна 37.
Так как плоскость сечения проведена через среднюю линию, то она делит боковую плоскость пополам. Следовательно, площадь боковой поверхности большей призмы в 2 раза больше площадь боковой поверхности малой призмы и равна 74.
Библиографическое описание:
Данилко, В. А. Расчет площади поверхности сложных деталей / В. А. Данилко. — Текст : непосредственный // Молодой ученый. — 2022. — № 16 (411). — С. 4-7. — URL: https://moluch.ru/archive/411/90473/ (дата обращения: 15.05.2023).
В работе осуществлен анализ способов измерения площади поверхности различных фигур. Представлен авторский метод расчета площади поверхности фигуры как площади поверхности вращения с предварительным аналитическим описанием контура фигуры.
Ключевые слова:площадь поверхности вращения, интегралы, тела сложной формы.
Для решения определённого рода задач гальваники и металлообработки требуется знать площадь поверхности тела, с которым придётся работать. Однако, не всегда получается быстро осуществить вычисления, ввиду того что некоторые детали имеют нетипичную, сложную форму. Поэтому возникает необходимость найти максимально простой, удобный и экономически выгодный способ для определения этой площади.
Существуют различные подходы к решению данной проблемы. Например, Яскеляин Б. В. и Череднеченко Т. Ф. предложили способ измерения площади поверхности тела, при котором на тело наносят плёнку из материала постоянной толщины, обладающего свойством гигроскопичности, предварительно покрывая поверхность смачивающим составом. Площадь поверхности при этом находят из её геометрической площади с учётом отношения приращения длины плёнки к геометрической длине поверхности [1].
Другой способ был предложен В. Г. Вохмяниным [2]. Он заключался в измерении веса двух тел, простого эталонного (образцового) и измеряемого (сложной формы). Сначала в обычных условиях измеряли вес тел, а затем их охлаждали до температуры конденсации воды и снова проводили взвешивание. Площадь вычисляли, находя частное от деления изменения веса измеряемого тела на изменение веса эталонного. При этом полученное число — это площадь поверхности, выраженная в единицах эталонного тела. Данный способ по сравнению с аналогичными отличается высокой производительностью, простотой, низкой стоимостью и высокой точностью.
Способ измерения площади поверхности, предложенный В. С. Аксельродом и Г. М. Рохлиной [3] позволяет измерить площадь плоской детали сложной формы и основывается на измерении емкости конденсатора. Площадь изделия равна произведению отношения емкости конденсаторов, одной из обкладок которых является измеряемое изделие или эталонное изделие.
Е. Д. Гражданников предложил способ определения величины поверхности твёрдых тел, основанный на измерении сокращения времён спин-решёточной и спин-спиновой магнитной релаксации ядер в слое жидкости, покрывающей поверхность твёрдой фазы [4]. Данный способ предназначен для определения поверхности широкого круга нанесённых веществ и носителей, причём измерения могут быть проведены непосредственно в процессе реакции. Для определения по этому способу площади поверхности нужен эталон изделия, площадь поверхности которого можно измерить другим способом.
Б. Д. Разуваева и К. С. Лыткин, исследуя методы определения площади поверхности сложных изделий, пришли к выводу о том, что метод растворения достаточно надёжен в измерении площади поверхности детали [5]. Он основан на том, что количество металла, растворяющегося в жидкости за единицу времени пропорционально величине поверхности металла. Для определения по этому способу площади поверхности требуется эталонное изделие с известной площадью поверхности.
Каждый из представленных способов предполагает осуществление определенных химические операции с изделием, а также зачастую наличие эталонного тела. В то же время, обратившись к математическому инструментарию, можно осуществить расчет площади поверхности тела аналитически с меньшими затратами.
Например, если изделие обладает центральной симметрией, то его можно рассматривать, как тело вращения. Тогда площадь его поверхности можно рассчитать, как площадь поверхности вращения по формуле:
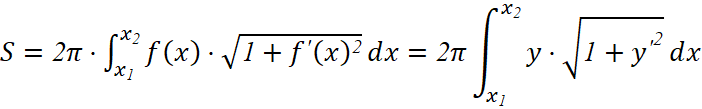
где — аналитическая функция, описывающая контур изделия,
x1 и x2 — границы, в которых задана функция.
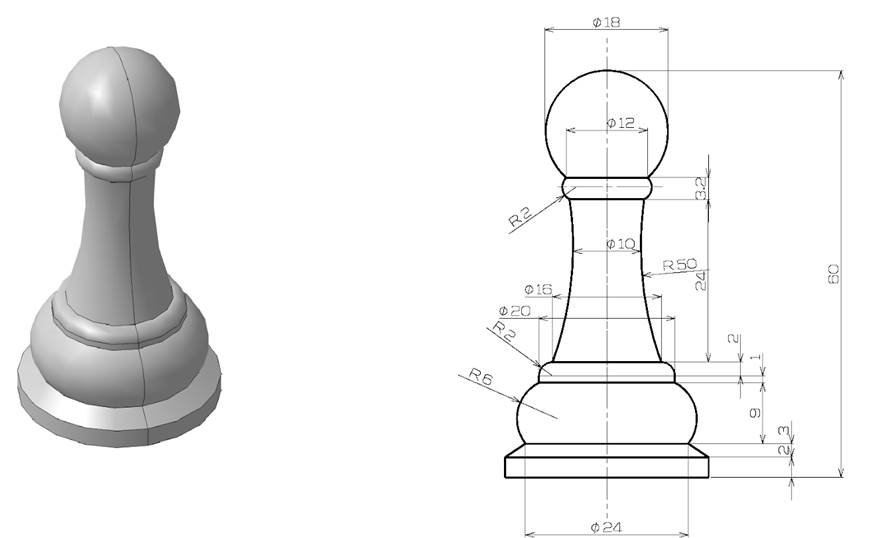
Рассмотрим более подробное применение данного способа на частном примере. Определим площадь поверхности шахматной пешки (рис.1.).
Рис. 1. Шахматная пешка
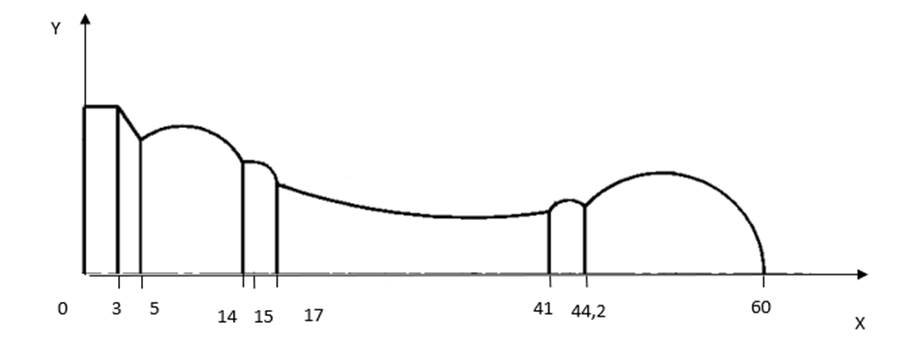
Поместим контур исследуемого тела в декартову систему координат XOY (рис.2.).
Разные участки контура можно задать различными функциями вида . Так можно выделить 8 таких функций, задающих контур боковой поверхности, для 8 участков. Так как ищем площадь боковой поверхности, то площадь основания фигуры не рассматриваем.
1) При — функция —
2) При — функция —
3) При — функция —
4) При — функция —
5) При — функция —
6) При — функция —
7) При — функция —
8) При — функция —
Рис. 2. Контур пешки в системе координат
Найдя данные функции, можно вычислить площадь поверхности этих участков. В ситуациях, когда функция имеет вид , площадь поверхности участка будет вычисляться также как площадь поверхности цилиндра, по формуле
, но в данном случае —
, а
, где
и
— координаты
начала и конца участка соответственно.
Так, для первого и четвёртого участков площадь поверхности равна соответственно: ,
.
Для других участков будет использоваться формула вычисления площади поверхности вращения вдоль оси OX.
Так вычисляем площадь поверхности второго участка:
Далее, аналогично, получаем значения площади поверхности остальных участков:
,
,
,
,
.
Конечную площадь поверхности находим как сумму площадей поверхностей участков:
.
Данный способ может быть использован для определения площади поверхности тел наряду с ранее упомянутыми. Он будет особенно удобен в случае, если изделие имеет центральную симметрию. Метод отличается точностью и экономической выгодой.
Литература:
1. Яскеляин Б. В., Чередненко Т. Ф. Способ измерения площади поверхности тела сложной формы [Электронный ресурс] // НЭБ: Национальная электронная библиотека — URL: https://rusneb.ru/catalog/000224_000128_0093005691_19950720_A_RU/ (дата обращения 22.02.2022)
2. Вохмянин В. Г. Способ В. Г. Вохмянина измерения площади поверхности тела сложной формы [Электронный ресурс] // FREEPATENT: патентный поиск в РФ — URL: https://www.freepatent.ru/patents/2040776 (дата обращения 22.02.2022)
3. Аксельрод В. С., Рохлина Г. М. Способ определения площади поверхности электропроводящих изделий [Электронный ресурс] // НЭБ: Национальная электронная библиотека — URL: https://viewer.rusneb.ru/ru/000224_000128_0000273447_19700615_A1_SU?page=1&rotate=0&theme=white (дата обращения 22.02.2022)
4. Гражданников Е. Д. Способ определения величины поверхности твёрдых тел [Электронный ресурс] // НЭБ: Национальная электронная библиотека — URL: https://viewer.rusneb.ru/ru/000224_000128_0000176457_19651102_A1_SU?page=1&rotate=0&theme=white (дата обращения 22.02.2022)
5. Разуваева Б. Д., Лыткин К. С. Экспресс-метод измерения криволинейных и фактурных поверхностей [Электронный ресурс] // Драгоценные материалы — URL: http://jewelpreciousmetal.ru/technology_other_surfacearea.php ((дата обращения 22.02.2022)
Основные термины (генерируются автоматически): площадь поверхности, сложная форма, функция, площадь поверхности вращения, XOY, боковая поверхность, центральная симметрия, шахматная пешка, эталонное изделие, эталонное тело.
Определения площади поверхностей изделий
Определения площади поверхностей изделий
Вычисления площади поверхностей изделий проводят определением размеров деталей изделий с помощью линейки и штангенциркуля.
Площади поверхности изделий, имеющие простые формы геометрических тел (цилиндр, конус пирамида и. т. д.) определяются по известным из математики формулам.
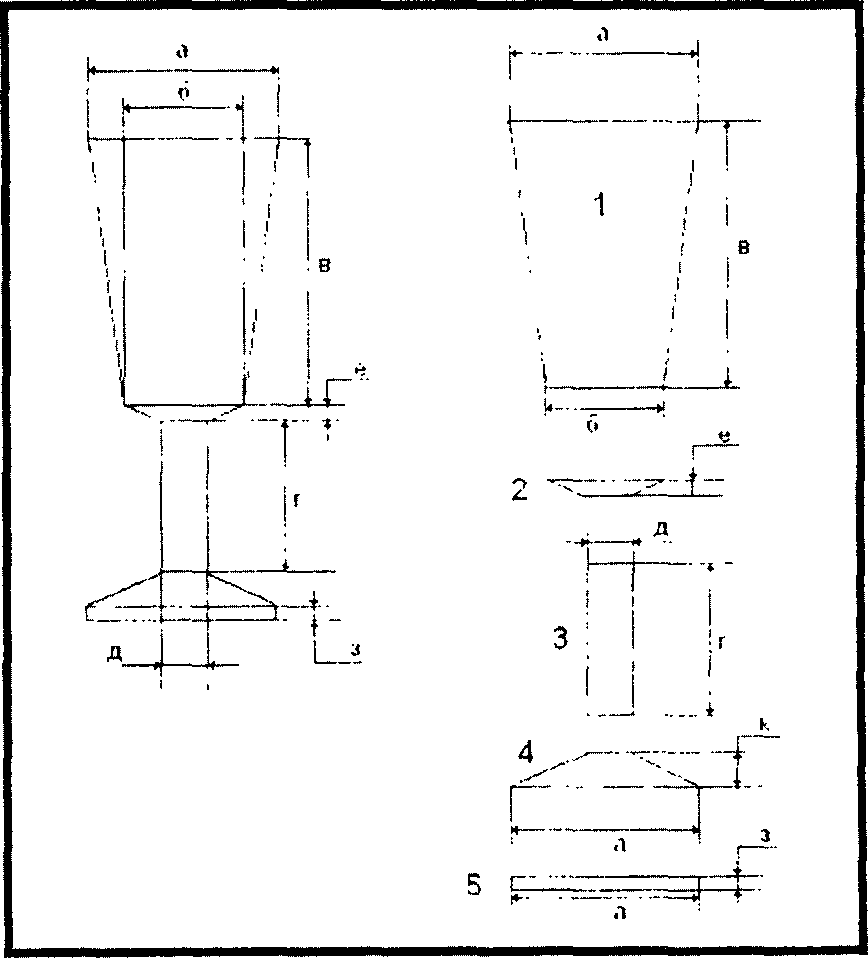
Например, для определения площади поверхности рюмки (рис. 1.1), условно разбиваем ее на простые геометрические фигуры. После подсчетов площадей поверхности фигур полученные величины складываем: S=S
+S:-
-S3+S
-S5.
Поверхностями малых участков изделия пренебрегаем. Участки изделий, имеющие неправильные формы (рис. 1.2: 1.3). приближенно приравниваем к более простым фигурам прямом ольнику. конусу призме и т.д.
Полученную величину площади поверхности изделия в мм” надо разделить на 10000, чтобы получить площадь в дм
 |
|
Рис. 1.1. Схема рюмки и детали рюмки |
 |
|
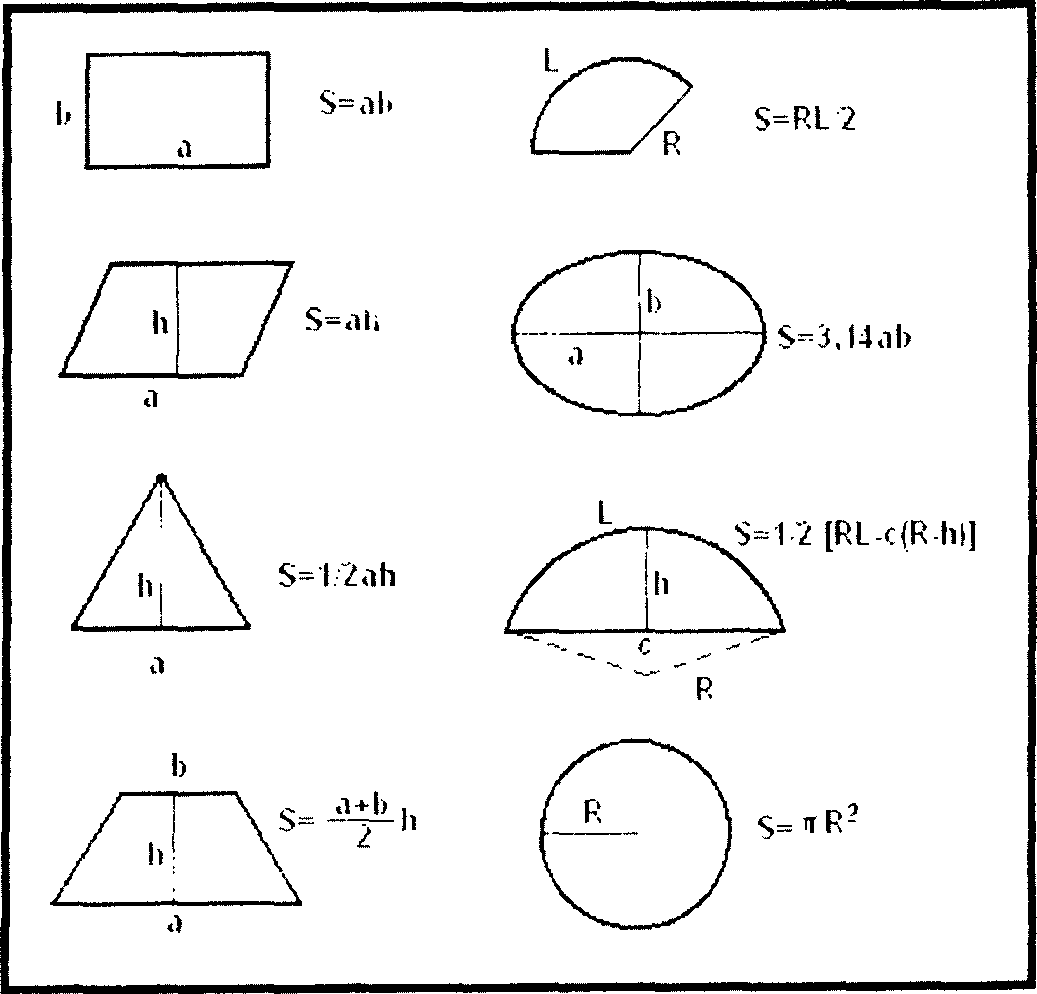
Рис. 1.2.Площади плоских фигур |
 |
|
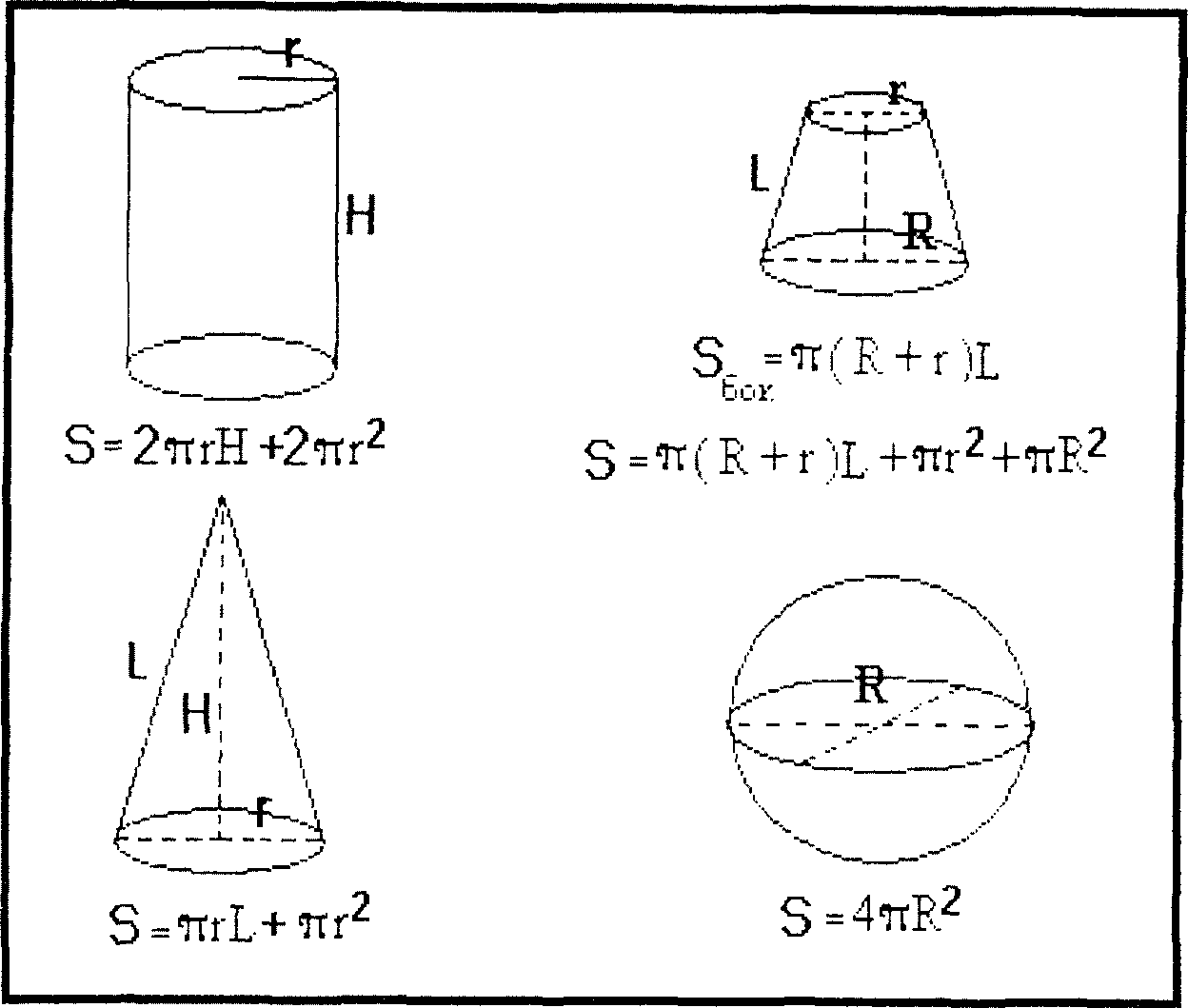
Рис. 1.3. Площади объемных фигур |
1.4.
Содержание:
Площади поверхностей геометрических тел:
Под площадью поверхности многогранника мы понимаем сумму площадей всех его граней. Как же определить площадь поверхности тела, не являющегося многогранником? На практике это делают так. Разбивают поверхность на такие части, которые уже мало отличаются от плоских. Тогда находят площади этих частей, как будто они являются плоскими. Сумма полученных площадей является приближенной площадью поверхности. Например, площадь крыши здания определяется как сумма площадей кусков листового металла. Еще лучше это видно на примере Земли. Приблизительно она имеет форму шара. Но площади небольших ее участков измеряют так, как будто эти участки являются плоскими. Более того, под площадью поверхности тела будем понимать предел площадей полных поверхностей описанных около него многогранников. При этом должно выполняться условие, при котором все точки поверхности этих многогранников становятся сколь угодно близкими к поверхности данного тела. Для конкретных тел вращения понятие описанного многогранника будет уточнено.
Понятие площади поверхности
Рассмотрим периметры
Применим данные соотношения к обоснованию формулы для площади боковой поверхности цилиндра.
При вычислении объема цилиндра были использованы правильные вписанные в него призмы. Найдем при помощи в чем-то аналогичных рассуждений площадь боковой поверхности цилиндра.
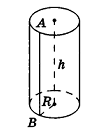
Опишем около данного цилиндра радиуса R и высоты h правильную n-угольную призму (рис. 220).
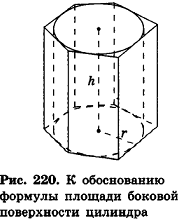
Площадь боковой поверхности призмы равна
где 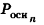
При неограниченном возрастании n получим:
так как периметры оснований призмы стремятся к длине окружности основания цилиндра, то есть к
Учитывая, что сумма площадей двух оснований призмы стремится к 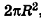
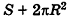
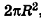
Итак, площадь боковой поверхности цилиндра вычисляется по формуле
где R — радиус цилиндра, h — его высота.
Заметим, что эта формула аналогична соответствующей формуле площади боковой поверхности прямой призмы
За площадь полной поверхности цилиндра принимается сумма площадей боковой поверхности и двух оснований:
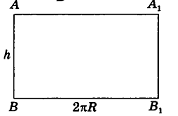
Если боковую поверхность цилиндра радиуса R и высоты h разрезать по образующей АВ и развернуть на плоскость, то в результате получим прямоугольник 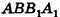
Очевидно, что сторона 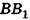
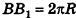
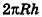
Пример:
Параллельно оси цилиндра на расстоянии d от нее проведена плоскость, отсекающая от основания дугу 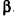
Решение:
Пусть дан цилиндр, в основаниях которого лежат равные круги с центрами 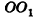
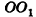
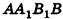
Пусть хорда АВ отсекает от окружности основания дугу 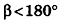
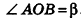
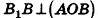
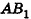
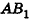
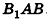
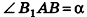
В равнобедренном треугольнике 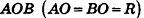
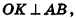
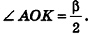
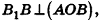
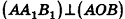
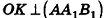
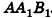
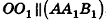
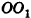
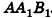
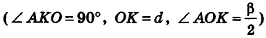
откуда 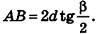
Итак,
В случае, когда
Аналогично предыдущему, и в этом случае получаем тот же результат для площади боковой поверхности.
Ответ:
Площадь поверхности конуса и усеченного конуса
Связь между цилиндрами и призмами полностью аналогична связи между конусами и пирамидами. В частности, это касается формул для площадей их боковых поверхностей.
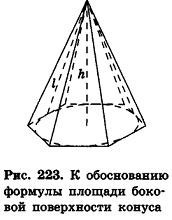
Опишем около данного конуса с радиусом основания R и образующей I правильную л-угольную пирамиду (рис. 223). Площадь ее боковой поверхности равна
где 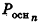
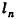
При неограниченном возрастании n получим:
так как периметры оснований пирамиды стремятся к длине окружности основания конуса, а апофемы 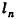
Учитывая, что площадь основания пирамиды стремится к 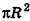
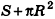
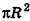
где R — радиус основания, I — образующая.
За площадь полной поверхности конуса принимается сумма площадей его основания и боковой поверхности:
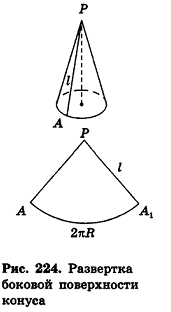
Если боковую поверхность конуса разрезать по образующей РА и развернуть на плоскость, то в результате получим круговой сектор 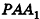
Очевидно, что радиус сектора развертки равен образующей конуса I, а длина дуги 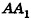
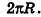
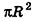
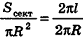
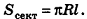
Учитывая формулу для площади боковой поверхности конуса, нетрудно найти площадь боковой поверхности усеченного конуса.
Рассмотрим усеченный конус, полученный при пересечении конуса с вершиной Р некоторой секущей плоскостью (рис. 225).
Пусть 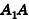
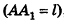
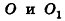
Из подобия треугольников
следует, что
Тогда получаем
Таким образом,
Итак, мы получили формулу для вычисления площади боковой поверхности усеченного конуса: 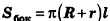
Отсюда ясно, что площадь полной поверхности усеченного конуса равна
Такой же результат можно было бы получить, если найти площадь развертки боковой поверхности усеченного конуса или использовать правильные усеченные пирамиды, описанные около него. Попробуйте дать соответствующие определения и провести необходимые рассуждения самостоятельно.
Связь между площадями поверхностей и объемами
При рассмотрении объемов и площадей поверхностей цилиндра и конуса мы видели, что существует тесная взаимосвязь между этими фигурами и призмами и пирамидами соответственно. Оказывается, что и сфера (шар), вписанная в многогранник, связана с величиной его объема.
Определение:
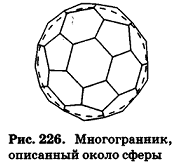
Сфера (шар) называется вписанной в выпуклый многогранник, если она касается каждой его грани.
При этом многогранник называется описанным около данной сферы (рис. 226).
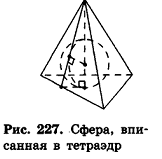
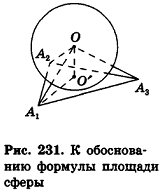
Рассмотрим, например, сферу, вписанную в тетраэдр (рис. 227).
Плоскости, содержащие грани тетраэдра, являются касательными к вписанной сфере, а точки касания лежат в гранях тетраэдра. Заметим, что по доказанному в п. 14.2 радиусы вписанной сферы, проведенные в точку касания с поверхностью многогранника, перпендикулярны плоскостям граней этого многогранника.
Для описанных многоугольников на плоскости было доказано, что их площадь равна произведению полупериметра на радиус вписанной окружности. Аналогичное свойство связывает объем описанного многогранника и площадь его поверхности.
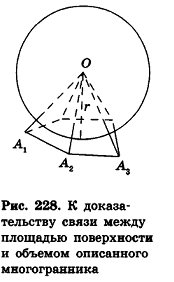
Теорема (о связи площади поверхности и объема описанного многогранника)
Объем описанного многогранника вычисляется по формуле
где 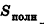
Доказательство:
Соединим центр вписанной сферы О со всеми вершинами многогранника 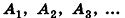
где 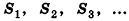
Теорема доказана.
Оказывается, что в любой тетраэдр можно вписать сферу, и только одну. Но не каждый выпуклый многогранник обладает этим свойством.
Рассматривают также сферы, описанные около многогранника.
Определение:
Сфера называется описанной около многогранника, если все его вершины лежат на сфере.
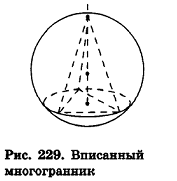
При этом многогранник называется вписанным в сферу (рис. 229).
Также считается, что соответствующий шар описан около многогранника.
Около любого тетраэдра можно описать единственную сферу, но не каждый многогранник обладает соответствующим свойством.
Площадь сферы
Применим полученную связь для объемов и площадей поверхностей описанных многогранников к выводу формулы площади сферы.
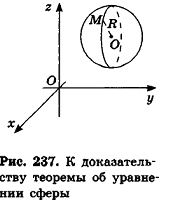
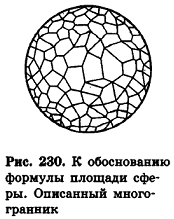
Опишем около сферы радиуса R выпуклый многогранник (рис. 230).
Пусть S’ — площадь полной поверхности данного многогранника, а любые две точки одной грани удалены друг от друга меньше чем на е. Тогда объем многогранника равен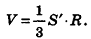
По неравенству треугольника 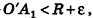
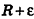
Итак, объем V данного многогранника больше объема шара радиуса R и меньше объема шара радиуса 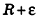
Отсюда получаем
Если неограниченно уменьшать размеры граней многогранника, то есть при е, стремящемся к нулю, левая и правая части последнего неравенства будут стремиться к 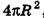
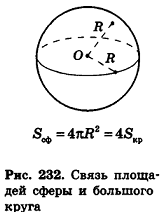
Итак, площадь сферы радиуса R вычисляется по формуле
Доказанная формула означает, что площадь сферы равна четырем площадям ее большого круга (рис. 232).
Исходя из аналогичных рассуждений, можно получить формулу для площади сферической части шарового сегмента с высотой Н:
Оказывается, что эта формула справедлива и для площади сферической поверхности шарового слоя (пояса):
где Н — высота слоя (пояса).
Справочный материал
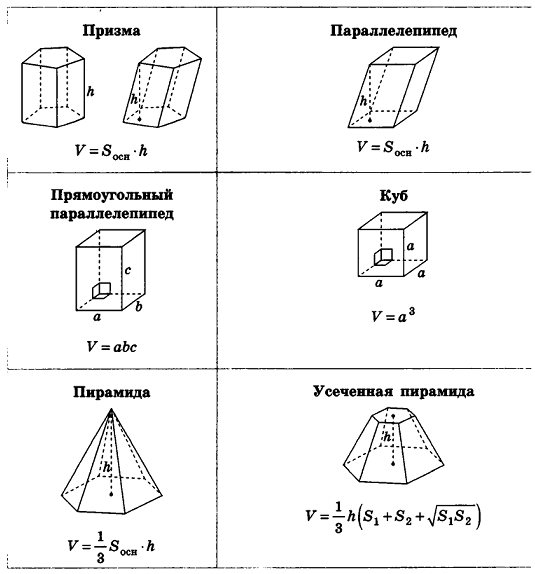
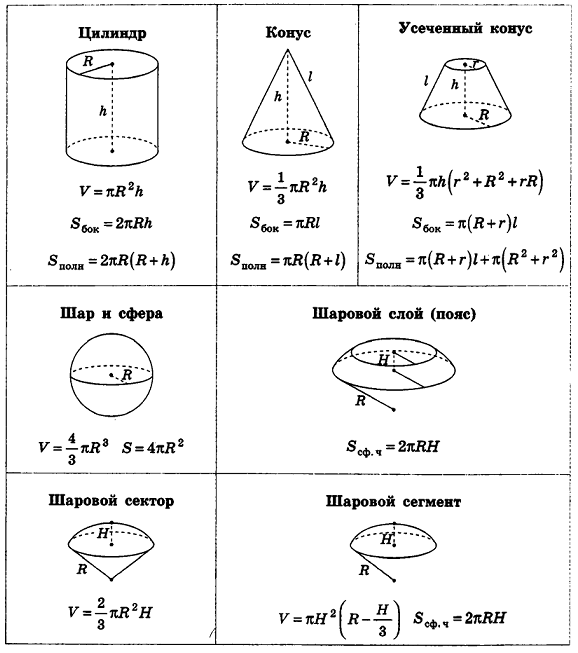
Формулы объемов и площадей поверхностей геометрических тел
Историческая справка
Многие формулы для вычисления объемов многогранников были известны уже в Древнем Египте. В так называемом Московском папирусе, созданном около 4000 лет назад, вероятно, впервые в истории вычисляется объем усеченной пирамиды. Но четкие доказательства большинства формул для объемов появились позднее, в работах древнегреческих ученых.
Так, доказательства формул для объемов конуса и пирамиды связаны с именами Демокрита из Абдеры (ок. 460-370 гг. до н. э.) и Евдокса Книдского (ок. 408-355 гг. до н. э.). На основании их идей выдающийся математик и механик Архимед (287-212 гг. до н. э.) вычислил объем шара, нашел формулы для площадей поверхностей цилиндра, конуса, сферьГг
Дальнейшее развитие методы, предложенные Архимедом, получили благодаря трудам средневекового итальянского монаха и математика Бонавентуры Кавальери (1598-1647). В своей книге «Геометрия неделимых» он сформулировал принцип сравнения объемов, при котором используются площади сечений. Его рассуждения стали основой интегральных методов вычисления объемов, разработанных Исааком Ньютоном (1642 (1643)-1727) и Готфридом Вильгельмом фон Лейбницем (1646-1716). Во многих учебниках по геометрии объем пирамиды находится с помощью * чертовой лестницы» — варианта древнегреческого метода вычерпывания, предложенного французским математиком А. М. Лежандром (1752-1833).
На II Международном конгрессе математиков, который состоялся в 1900 году в Париже, Давид Гильберт сформулировал, в частности, такую проблему: верно ли, что любые два равновеликих многогранника являются равносоставленными? Уже через год отрицательный ответ на этот вопрос был обоснован учеником Гильберта Максом Деном (1878-1952). Другое доказательство этого факта предложил в 1903 году известный геометр В. Ф. Каган, который в начале XX века вел плодотворную научную и просветительскую деятельность в Одессе. В частности, из работ Дена и Кагана следует, что доказательство формулы объема пирамиды невозможно без применения пределов.
Весомый вклад в развитие теории площадей поверхностей внесли немецкие математики XIX века. Так, в 1890 году Карл Герман Аман-дус Шварц (1843-1921) построил пример последовательности многогранных поверхностей, вписанных в боковую поверхность цилиндра («сапог Шварца»). Уменьшение их граней не приводит к приближению суммы площадей этих граней к площади боковой поверхности цилиндра. Это стало толчком к созданию выдающимся немецким математиком и физиком Германом Минков-ским (1864-1909) современной теории площадей поверхностей, в которой последние связаны с объемом слоя около данной поверхности.
Учитывая огромный вклад Архимеда в развитие математики, в частности теории объемов и площадей поверхностей, именно его изобразили на Филдсовской медали — самой почетной в мире награде для молодых математиков. В 1990 году ею был награжден Владимир Дрин-фельд (род. в 1954 г.), который учился и некоторое время работал в Харькове. Вот так юные таланты, успешно изучающие геометрию в школе, становятся в дальнейшем всемирно известными учеными.
Уравнения фигур в пространстве
Напомним, что уравнением фигуры F на плоскости называется уравнение, которому удовлетворяют координаты любой точки фигуры F и не удовлетворяют координаты ни одной точки, не принадлежащей фигуре F. Так же определяют и уравнение фигуры в пространстве; но, в отличие от плоскости, где уравнение фигуры содержит две переменные х и у, в пространстве уравнение фигуры является уравнением с тремя переменными х, у и z.
Выведем уравнение плоскости, прямой и сферы в пространстве. Для получения уравнения плоскости рассмотрим в прямоугольной системе координат плоскость а (рис. 233) и определим свойство, с помощью которого можно описать принадлежность произвольной точки данной плоскости. Пусть ненулевой вектор 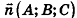
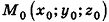
Так как 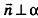
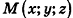
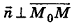
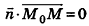
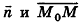
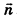
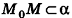
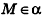
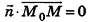
Теорема (уравнение плоскости в пространстве)
В прямоугольной системе координат уравнение плоскости имеет вид 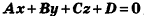
Доказательство:
Запишем в координатной форме векторное равенство 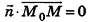
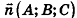
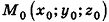
Следовательно,
После раскрытия скобок и приведения подобных членов это уравнение примет вид:
Обозначив числовое выражение в скобках через D, получим искомое уравнение, в котором числа А, В и С одновременно не равны нулю, так как 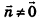
Покажем теперь, что любое уравнение вида Ах + Ву +Cz+D = 0 задает в пространстве плоскость. Действительно, пусть 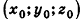
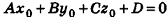
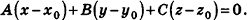
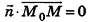
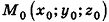
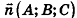
Обратим внимание на то, что в доказательстве теоремы приведен способ составления уравнения плоскости по данным координатам произвольной точки плоскости и вектора нормали.
Пример:
Напишите уравнение плоскости, которая перпендикулярна отрезку MN и проходит через его середину, если М{-1;2;3), N(5;-4;-1).
Решение:
Найдем координаты точки О — середины отрезка MN:
Значит, О (2; -1; l). Так как данная плоскость перпендикулярна отрезку MN, то вектор 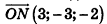
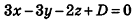
И наконец, так как данная плоскость проходит через точку О(2;-l;l), то, подставив координаты этой точки в уравнение, получим:
Таким образом, уравнение 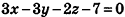
Ответ:
Заметим, что правильным ответом в данной задаче является также любое уравнение, полученное из приведенного умножением обеих частей на число, отличное от нуля.
Значения коэффициентов А, В, С и D в уравнении плоскости определяют особенности расположения плоскости в системе координат. В частности:
- если
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
- если один из коэффициентов А, В и С равен нулю, a
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
перпендикулярен оси Ох, а плоскость By + Cz + D = Q параллельна оси Ох (рис. 234, б)
- если два из коэффициентов А, В и С равны нулю, а
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
перпендикулярен плоскости Оху, а плоскость Cz+D = 0 параллельна плоскости Оху (рис. 234, в);
- если два из коэффициентов А, В и С равны нулю и D = 0, плоскость совпадает с одной из координатных плоскостей: например, при условиях
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
Предлагаем вам самостоятельно составить полную таблицу частных случаев расположения плоскости Ax + By+Cz+D = 0 в прямоугольной системе координат в зависимости от значений коэффициентов А, В, С и D.
Пример: (о расстоянии от точки до плоскости)
Расстояние от точки 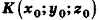
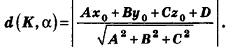
Решение:
Если 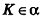
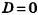
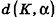
Если 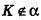
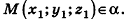
Тогда 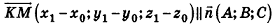
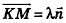
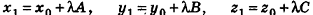
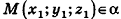
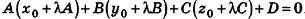
Таким образом,
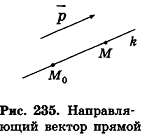
Рассмотрим теперь возможность описания прямой в пространстве с помощью уравнений.
Пусть в пространстве дана прямая k (рис. 235). Выберем ненулевой вектор 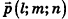
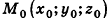
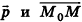
Представим это векторное равенство в координатной форме. Если ни одна из координат направляющего вектора не равна нулю, из данного равенства можно выразить t и приравнять полученные результаты:
Эти равенства называют каноническими уравнениями прямой в пространстве.
Пример:
Напишите уравнение прямой, проходящей через точки А(1;-3;2) и В(-l;0;l).
Решение:
Так как точки А и В принадлежат данной прямой, то 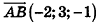
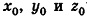
Ответ:
Заметим, что ответ в этой задаче может иметь и другой вид: так, в числителях дробей можно использовать координаты точки В, а как направляющий вектор рассматривать любой ненулевой вектор, коллинеарный 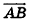
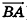
Вообще, если прямая в пространстве задана двумя точками 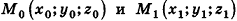
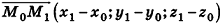
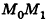
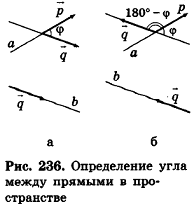
С помощью уравнений удобно исследовать взаимное расположение прямых и плоскостей в пространстве. Рассмотрим прямые 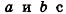
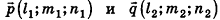
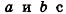
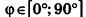
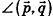
Так как cos(l80°-ф) = -coscp, имеем 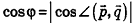
Отсюда, в частности, следует необходимое и достаточное условие перпендикулярности прямых 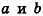
Кроме того, прямые 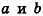
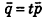
Проанализируем теперь отдельные случаи взаимного расположения двух плоскостей в пространстве. Очевидно, что если 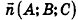
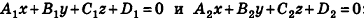
- совпадают, если существует число t такое, что
, или, если числа
ненулевые
- параллельны, если существует число t такое, что
, или, если координаты
ненулевые,
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
).
В остальных случаях данные плоскости 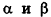
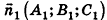
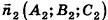
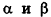
В частности, необходимое и достаточное условие перпендикулярности плоскостей 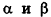
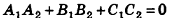
Заметим также, что прямая в пространстве может быть описана как линия пересечения двух плоскостей, то есть системой уравнений
где векторы 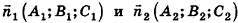
Пример:
Напишите уравнение плоскости, которая проходит через точку М(4;2;3) и параллельна плоскости x-y + 2z-S = 0.
Решение:
Так как искомая плоскость параллельна данной, то вектор нормали к данной плоскости 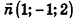
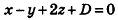
Ответ: x-y+2z-8 = 0.
Аналогично уравнению окружности на плоскости, в пространственной декартовой системе координат можно вывести уравнение сферы с заданным центром и радиусом.
Теорема (уравнение сферы)
В прямоугольной системе координат уравнение сферы радиуса R с центром в точке 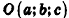
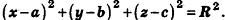
Пусть 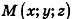
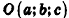
Так как OM=R, то есть ОМ2 = R2, то координаты точки М удовлетворяют уравнению 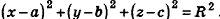
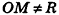
Следствие
Сфера радиуса R с центром в начале координат задается уравнением вида
Заметим, что фигуры в пространстве, как и на плоскости, могут задаваться не только уравнениями, но и неравенствами. Например, шар радиуса R с центром в точке 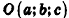
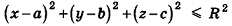
Пример:
Напишите уравнение сферы с центром А (2;-8; 16), которая проходит через начало координат.
Решение:
Так как данная сфера проходит через точку 0(0;0;0), то отрезок АО является ее радиусом. Значит,
Таким образом, искомое уравнение имеет вид:
Ответ:
Доказательство формулы объема прямоугольного параллелепипеда
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
где 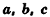
Доказательство:
Докажем сначала, что объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
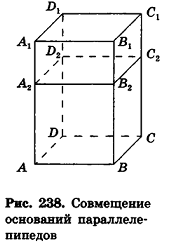
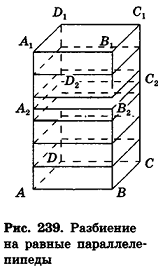
Пусть 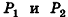
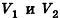
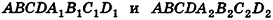
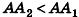
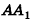
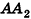
проведем через точки деления параллельные основанию ABCD (рис. 239). Они разобьют параллелепипед 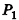
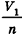
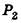
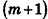
Таким образом, 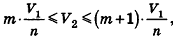
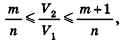
Сравнивая выражения (1) и (2), видим, что оба отношения 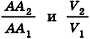
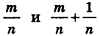
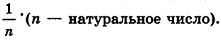
Допустим, что это не так, то есть 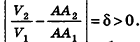
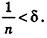
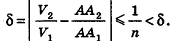
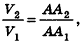
Рассмотрим теперь прямоугольные параллелепипеды с измерениями 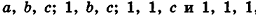
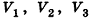
По аксиоме объема V3 =1. По доказанному 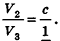
Теорема доказана.
* Выберем 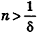
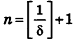
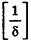
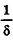
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Многоугольник
- Площадь многоугольника
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии







































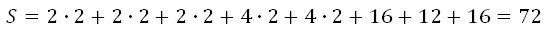
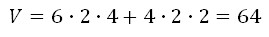
























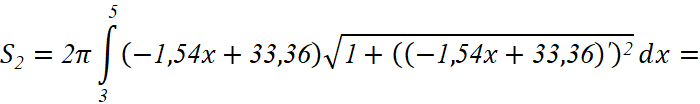
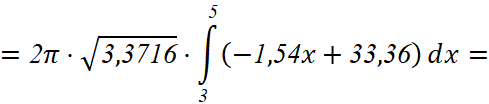
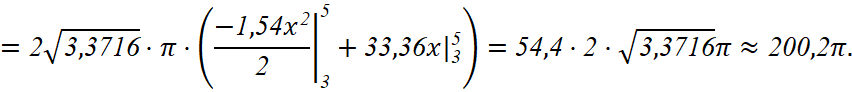
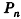
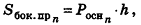
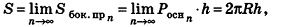
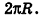
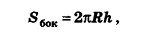
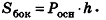
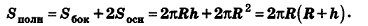

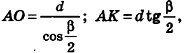
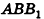
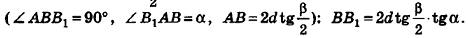
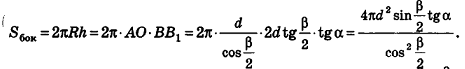
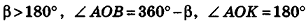
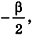
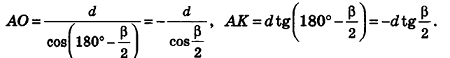
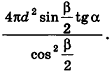
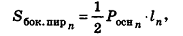
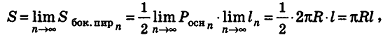
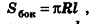
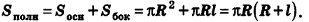
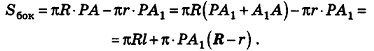
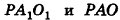
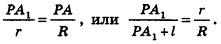
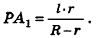
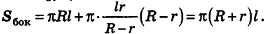
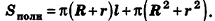
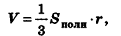
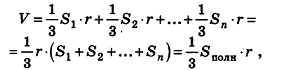
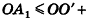
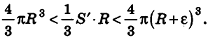
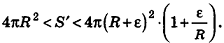
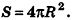
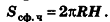
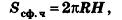






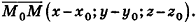
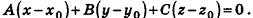
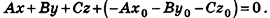
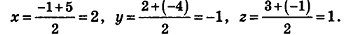
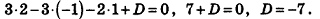
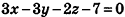
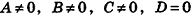 , уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);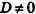 , плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали 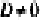 , плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали 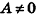 и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).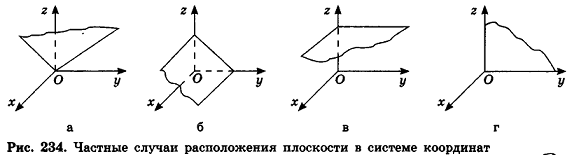
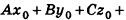
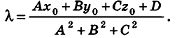
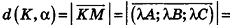
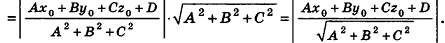
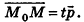
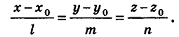
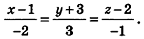
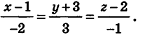
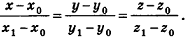
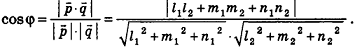
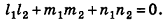
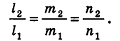
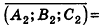
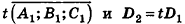 , или, если числа
, или, если числа 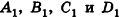 ненулевые
ненулевые 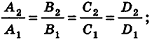
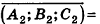
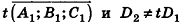 , или, если координаты
, или, если координаты 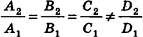 (на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где 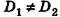 ).
).