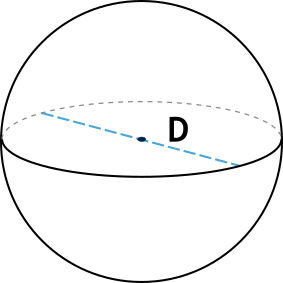
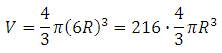Шаром называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее RR — радиус этого шара.
Онлайн-калькулятор площади поверхности шара
У шара, как и у круга, есть диаметр DD, который по длине в два раза превосходит радиус шара.
D=2⋅RD=2cdot R
Площадь поверхности шара можно найти используя как радиус, так и диаметр шара.
Формула площади поверхности шара по радиусу шара
S=4⋅π⋅R2S=4cdotpicdot R^2
RR — радиус шара.
Шар вписан в куб, диагональ которого dd равна 300sqrt{300} (см.). Найти площадь поверхности шара.
Решение
d=300d= sqrt{300}
Первым шагом в решении задачи будет нахождение длины стороны куба. Обозначим ее через aa. Тогда, по теореме Пифагора:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
a=d3a=frac{d}{sqrt{3}}
a=3003=100=10a=frac{sqrt{300}}{sqrt{3}}=sqrt{100}=10
Радиус шара, вписаного в куб равен половине стороны этого куба:
R=a2=102=5R=frac{a}{2}=frac{10}{2}=5
Тогда площадь поверхности шара:
S=4⋅π⋅R2=4⋅π⋅52≈314S=4cdotpicdot R^2=4cdotpicdot 5^2approx314 (см. кв.)
Ответ: 314 см. кв.
Формула площади поверхности шара по диаметру шара
Формулу для площади поверхности шара легко получить через его диаметр, пользуясь соотношением между радиусом и диаметром шара:
S=4⋅π⋅R2=4⋅π⋅(D2)2=π⋅D2S=4cdotpicdot R^2=4cdotpicdotBig(frac{D}{2}Big)^2=picdot D^2
S=π⋅D2S=picdot D^2
DD — диаметр шара.
Диаметр шара равен 10 (см.). Найдите площадь его поверхности.
Решение
D=10D=10
По формуле получаем:
S=π⋅D2=π⋅102≈314S=picdot D^2=picdot 10^2approx314 (см. кв.)
Ответ: 314 см. кв.
Студворк – лучший сайт для заказа контрольных работ!
Тест по теме «Площадь поверхности шара»
Если в условии речь идёт о единичном кубе, то это означает, что ребро этого куба равно единице; если речь идёт о единичной сфере, то это означает, что её радиус равен единице. Формулы площади и объёма шара смотрите здесь.
Площадь большого круга шара равна 17. Найдите площадь поверхности шара.
Мы знаем, что площадь поверхности шара находится по формул:
Необходимо найти радиус шара. Площадь осевого сечения (больший круг) равна 17. Из формулы площади круга можем найти его радиус.
Радиус большого круга является радиусом шара. Таким образом:
*Можно было сразу без данных вычислений сделать вывод, что площадь поверхности шара в 4 раза больше площади поверхности большого круга.
Ответ: 48
Во сколько раз увеличится площадь поверхности шара, если его радиус увеличить в три раза?
Запишем площадь поверхности исходного шара:
Площадь поверхности шара с радиусом втрое большим равна:
Таким образом, площадь поверхности шара увеличится в 9 раз.
Ответ: 9
Во сколько раз увеличится объем шара, если его радиус увеличить в шесть раз?
Объем шара находится по формуле:
При увеличении радиуса в шесть раз его объём будет:
Таким образом, объем шара увеличится в 216 раз.
Ответ: 216
Объем одного шара в 216 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Формула объёма шара:
Формула площади поверхности шара:
Пусть объёмы шаров соответственно равны:
Из условия следует, что:
То есть, мы установили, что радиус первого больше радиуса второго в 6 раз. Если радиус шара уменьшить в 6 раз, то площадь поверхности шара изменится следующим образом:
То есть она уменьшится в 36 раз.
Ещё один вариант рассуждения.
Объемы шаров (а так же их радиусов) соотносятся как:
То есть радиус одного шара в 6 раза больше другого.
Формула площади поверхности шара:
Если радиус одного шара увеличить в 6 раз, то площадь поверхности изменится следующим образом:
То есть она увеличится в 36 раз. Таким образом, площадь поверхности первого шара больше площади поверхности второго в 36 раз.
Ответ: 36
27073. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
Что необходимо отметить сразу же? Это то, что радиус цилиндра равен радиусу шара и высота цилиндра равна двум его радиусам.
Площадь поверхности шара находится по формуле:
То есть нам нужно найти радиус шара. Это можно сделать из формулы площади поверхности цилиндра:
*Как уже сказано, высота цилиндра равна двум радиусам, значит:
Как вы догадываетесь, сам радиус можно и не вычислять, и в формулу площади поверхности шара подставить лR2:
Ответ: 12
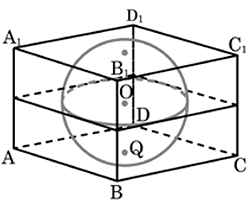
27105. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
Параллелепипед описанный около сферы является кубом. Формула объёма куба имеет вид:
Ребро данного куба равно диаметру сферы. Найдём его:
Таким образом, радиус сферы равен трём.
Ответ: 3
27126. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на Пи.
Ребро куба равно диаметру шара. Значит радиус шара равен 1,5. Вычислим объём шара:
Результат разделим на Пи и запишем ответ.
Ответ: 4,5
27059. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Посмотреть решение
27072. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Посмотреть решение
27097. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Посмотреть решение
27125. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Посмотреть решение
27162. Объем одного шара в 27 раз больше объема другого. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Посмотреть решение
27163. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Посмотреть решение
27174. Объем шара равен 288Пи. Найдите площадь его поверхности, деленную на Пи.
Посмотреть решение
27043. Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.
Посмотреть решение
27067. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Посмотреть решение
27127. Около куба с ребром равным корню из трёх описан шар. Найдите объем этого шара, деленный на Пи.
Посмотреть решение
Как видим, требуется знание формул и немножко логики. В будущем также будем рассматривать стереометрические задачи, не пропустите! На этом всё. Успеха Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Площадь поверхности шара
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности шара
Чтобы посчитать площадь поверхности шара (площадь сферы) воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чему равна площадь поверхности шара, если:
=
S =
0
Округление числа π: Округление ответа:
Просто введите известный вам параметр, и узнаете площадь сферы шара.
Теория
Ликбез: Поверхность шара — сфера.
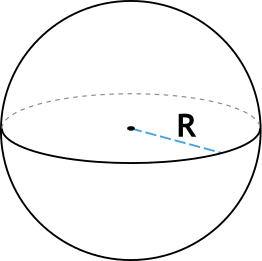
Площадь поверхности шара через радиус
Чему равна площадь поверхности шара Sпов, если его радиус r:
Формула
Sпов = 4⋅π⋅r² , где π ≈ 3.14…
Пример
Для примера посчитаем какая площадь поверхности у шара, если его радиус r = 3 см:
Sпов = 4 ⋅ 3.14 ⋅ 3² = 12.56 ⋅ 9 = 113.04 см²
Площадь поверхности шара через диаметр
Чему равна площадь поверхности шара Sпов, если его диаметр d?
Формула
Sпов = π⋅d² , где π ≈ 3.14…
Пример
Для примера посчитаем какая площадь поверхности у шара, если его диаметр d = 6 см:
Sпов = 3.14 ⋅ 6² = 3.14 ⋅ 36 = 113.04 см²
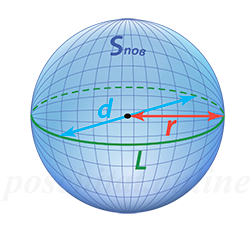
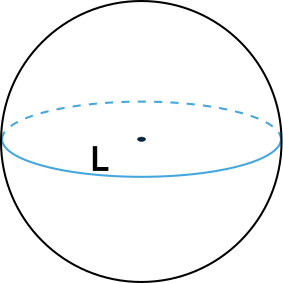
Площадь поверхности шара через длину окружности
Чему равна площадь поверхности шара Sпов, если длина его окружности L?
Формула
Sпов = L²⁄π , где π ≈ 3.14…
Пример
Для примера посчитаем чему равна площадь поверхности шара, имеющего длину окружности L = 10 см:
Sпов = 10² ⁄ 3.14 ≈ 31.85 см²
См. также
Площадь поверхности шара, или как часто неправильно говорят просто площадь шара, вычисляется по очень простой формуле. Но даже простые вещи можно упростить и именно поэтому мы сделали калькулятор, который в режиме онлайн может рассчитать площадь поверхности шара, а также на странице вы найдете формулу для расчета.
Возможно вам дополнительно потребуется рассчитать и объем шара.
Шар — геометрическое тело, состоящее из точек пространства, которые удалены от центра на расстояние, не более заданного. Это расстояние называют радиусом шара.
Содержание:
- калькулятор площади поверхности шара
- формула площади поверхности шара через радиус
- формула площади поверхности шара через диаметр
- формула площади поверхности шара через длину окружности
- примеры задач
Формула площади поверхности шара через радиус
{S = 4pi R^2}
R – радиус шара
Формула площади поверхности шара через диаметр
{S = pi D^2}
D – диаметр шара
Формула площади поверхности шара через длину окружности
{S = dfrac{L^2}{pi}}
L – длина окружности шара
Примеры задач на нахождение площади поверхности шара
Задача 1
Найдите площадь поверхности шара диаметром 10см.
Решение
Так как в условии дан диаметр шара, мы воспользуемся второй формулой.
S = pi D^2 = pi cdot 10^2 = pi cdot 100 = 100pi : см^2 approx 314.15927 : см^2
Ответ: 100pi : см^2 approx 314.15927 : см^2
калькулятор поможет проверить правильность вычислений.
Задача 2
Найдите площадь поверхности шара, если его радиус равен 5см.
Решение
В этой задаче мы будем использовать первую формулу.
S = 4pi R^2 = 4pi cdot 5^2 = 4pi cdot 25 = 100pi : см^2 approx 314.15927 : см^2
Ответ: 100pi : см^2 approx 314.15927 : см^2
Проверка ответа.
Ученик
(234),
закрыт
10 лет назад
Людмила Свердлова
Гуру
(2714)
13 лет назад
Площадь круга находится по формуле Sкр = пR^2, а площадь поверхности шара – Sш = 4пR^2. Радиус большого круга равен радиусу шара, значит площадь поверхности в 4 больше площади большого круга Sш = 4Sкр = 4*2 = 8. Ответ: 8.